Помехоустойчивость оптимального когерентного приема двоичных сигналов. Лекция №3

1.

кафедра информационнотелекоммуникационных систем и технологий
Дисциплина Анализ информационной безопасности
телекоммуникационных систем
Тема 2 Методы помехоустойчивого приема дискретных
сообщений
профессор
Белов Сергей Павлович
1

2.

Лекция №3 Помехоустойчивость оптимального когерентного
приема двоичных сигналов
ВОПРОСЫ
1. Потенциальная помехоустойчивость оптимального приемника.
2.Анализ помехоустойчивости оптимального приема двоичных
сигналов с различными видами модуляции.
ЦЕЛЬЮ
лекции
является
изучение
помехоустойчивости оптимального приема
различными видами модуляции.
принципов
оценки
двоичных сигналов с
Задачи лекции: изложение особенностей расчета помехоустойчивости
оптимального приема сигналов при наличии помех в виде белого шума.
Литература:
1 Белов, С.П., Жиляков, Е.Г. Анализ информационной безопасности
телекоммуникационных
систем:
Учебно-методический
комплекс. : http://pegas.bsu.edu.ru/course/view.php?id=8360
Белгород, 2015 год.
2 Скляр, Б. Цифровая связь. Теоретические основы и практическое
применение СПб, Киев,2003 год.

3.

Вопрос 1 Потенциальная помехоустойчивость оптимального
приемника
Определим потенциальную помехоустойчивость оптимального приемника
при передаче двоичных сигналов по каналу с постоянными параметрами в
условиях аддитивного гауссовского белого шума.
Предположим, что передавался сигнал S0 (t), соответствующий символу
«0», и на вход приемника поступает аддитивная смесь Z (t) = S0 (t) + n (t).
Ошибочное решение тогда будет принято, если
T
T
E0
E1
z
(
t
)
S
(
t
)
dt
z
(
t
)
S
(
t
)
dt
0
1
0
2 0
2
где
,i=0,1.
Преобразуем данное соотношение:
T
T
1
2
2
[
S
(
t
)
n
(
t
)][
S
(
t
)
S
(
t
)]
dt
[
S
(
t
)
S
0
1
0
1 (t )]dt ,
0 0
2 0
Отсюда
T
T
1
n
(
t
)[
S
(
t
)
S
(
t
)]
dt
[ S 0 (t ) S1 (t )]2 dt.
0
1
0
20
Введем предварительно обозначение
T
T
E2 S (t )dt , X n(t ) S (t )dt , тогда получим, что
2
0
0
,

4.

Вопрос1 Потенциальная помехоустойчивость оптимального
приемника
Несложно показать, что если сообщения «0» и «1» передаются
равновероятно, то при передаче символа «1» придем к этому же
соотношению. Иными словами, вероятности ошибки в обоих случаях
равны: P(1|0)=P(0|1)=P, т. е. сформированный в данном случае двоичный
дискретный канал является симметричным.
Величина Х имеет гауссовское распределение, так как она получена в
результате линейных преобразований над гауссовским случайным
процессом n(t). Её математическое ожидание
T
T
M X M n(t )S (t )dt M n(t ) S (t )dt 0 , так как M{n(t)} = 0.
0
0
Дисперсия величины Х
T
T
0
0
D{X}= S (t ) S ' (t ) M {n(t ) n ' (t )} dt dt '
Напомним, что функция корреляции белого шума вычисляется через
дельта - функцию, т. е.
N
B( ) M n(t )n(t ) 0 (t t )
2
Тогда
T T
T
N0
N0
N 0 Eэ
2
D X
(t t ) S (t ) S (t )dtdt
S
(
t
)
dt
2
2 0
2
0 0
E
E
а вероятность ошибки
t
2
2
E
1
X2
1
2
2
P P X э ( X )dX
2
2
dX
exp
2 D X
2 D X
e
2
x
2
dt Q( x)

5.

Вопрос1 Потенциальная помехоустойчивость оптимального
приемника
Здесь сделана замена переменной и введено обозначение
Учитывая, что Q( x) 1 F ( x) , где F ( x)
1
x
e
2
t2
2
dt - интеграл вероятностей,
для которого составлены подробные таблицы, окончательно запишем
выражение вероятности ошибочного приема при оптимальной процедуре
обработки
Eэ
,
P F
2N
0
где
- эквивалентная энергия сигналов.
Видно, что помехоустойчивость оптимального когерентного приемника
двоичных сигналов в условиях аддитивного шума определяется
отношением энергии сигнала к спектральной плотности мощности шума.
Помехоустойчивость больше у той системы, у которой эквивалентная
энергия сигналов больше, независимо от формы применяемых сигналов.
При расчетах вероятности ошибки по найденному соотношению следует
иметь в виду, что интеграл вероятности принимает следующие значения
F ( ) 0 , F (0) 0,5 , F ( ) 1 , F ( x) 1 F ( x)
Иногда в расчетах вместо функции F(x) используют другие, связанные с
этой функцией.

6.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
Полученные выше соотношения для вероятности ошибочного приема
конкретизируем для двоичных сигналов с различными видами манипуляции.
Рассмотрим наиболее часто применяемые сигналы с амплитудной, частотной,
фазовой и относительно-фазовой манипуляциями и рассчитаем их
помехоустойчивость.
2.1 Амплитудно-манипулированные сигналы
В этом случае один из двоичных сигналов, например S1(t) = 0. Данную и
подобные системы сигналов принято называть системой с пассивной паузой и
представлять в виде:
S 0 (t ) U c cos( 0t ) t 0, T
S1 (t ) 0
где Uc – амплитуда, ω – круговая частота, φ – начальная фаза сигнала
предполагаются полностью известными.
В двумерном пространстве сигналы с амплитудной манипуляцией (АМ) можно
представить в виде векторов (смотри рисунок 1).
Величина эквивалентной энергии АМ сигналов равна
T
Eэ E S 0 (t )dt.
2
Рисунок 1
Тогда вероятность ошибочного приема будет определяться соотношением
0
где
h2
Eэ
,
1 F
PАМ 1 F
2N
2
0
отношение энергии сигнала на входе приемника к спектральной
плотности мощности белого шума.

7.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
2.2 Частотно-манипулированные сигналы
В отличие от АМ сигналов эти сигналы называются сигналами с активной
паузой и описываются соотношением
S 0 (t ) U c cos( 0 t 0 ) S1 (t ) U c cos( 1t 1 t 0, T
,
,
Кроме того, они являются ортогональными, а это означает, что их скалярное
произведение равно нулю, т. е.
T
1
S0 , S1 S0 (t )S1 (t )dt 0
T 0
Пусть 0 2 K 0 T , 1 2 K1 T , где К0 и К1 – целые числа, φ0 и φ1 принимают
любые значения. Тогда
Это следует из того, что подынтегральные выражения содержат целое число
периодов косинусоид. Отсюда оба интеграла равны нулю, что и доказывает
ортогональность ЧМ сигналов. Определим величину эквивалентной энергии
данных сигналов. Эквивалентная энергия сигнала в этом случае равна:
так как последний интеграл по условию ортогональности равен нулю, а энергии
каждой реализации равны друг другу.

8.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
В двумерном пространстве ЧМ сигналы можно представить в виде
векторов, расположенных относительно друг друга под углом π/2. Именно
в этом случае их скалярное произведение равно нулю (рисунок 2).
Тогда вероятность ошибки равна
E
1 F
PЧМ 1 F
2
N
0
h
2
2.3 Фазоманипулированные сигналы
Рисунок 2
Так же как и ЧМ сигналы, фазоманипулированные сигналы являются
системой сигналов с активной паузой, поскольку каждой реализации
соответствует двоичный информационный символ «0» или «1». В
простейшем случае ФМ сигнал образуют путем скачкообразного
изменения фазы несущего колебания на 180◦. Получающийся в результате
сигнал представляет собой последовательность информационных
двухполярных посылок, умноженных на гармоническое несущее
колебание. Таким образом, ФМ сигналы имеют вид
S 0 (t ) U c cos( с t ),
S1 (t ) U c cos( t ) U c cos( c t ) t 0, T
Эти сигналы противоположные, так как S1(t)=-S0(t).
Их векторное представление показано на рисунке 3
Рисунок 3

9.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
Видно, что среди всех рассмотренных сигналов, фазоманипулированные
обладают наибольшим расстоянием между концами векторов в векторном
пространстве. Поэтому естественно ожидать, что они будут наиболее
различимыми и, соответственно, наиболее помехоустойчивыми.
Эквивалентную энергию ФМ сигналов определить несложно:
T
T
E э S 0 (t ) S1 (t ) dt 4 S 0 (t )dt 4 E
2
2
4E
1 F
Вероятность ошибки, следовательно, равна PФМ 1 F
2 N 0
t
x
1
e 2 dt
где F ( x)
2
0
0
2h
2
2
Если сравнить вероятности ошибок для ФМ, AM и ЧМ сигналов, то
нетрудно видеть, что последние занимают промежуточное место между
двумя первыми. При этом энергия при переходе от ФМ (противоположных)
к ЧМ (ортогональным) сигналам увеличивается в два раза, что
эквивалентно 3 дБ. Сравнение ЧМ и AM сигналов показывает, что для
обеспечения одинаковой верности приема при использовании ЧМ
сигналов потребуется энергии затратить в два раза меньше. Несмотря на
то, что ФМ сигналы являются самыми помехоустойчивыми, практическая
реализация их когерентного приема связана с серьезными трудностями,
возникающими при формировании опорного (эталонного) колебания,
синфазного с принимаемым сигналом.

10.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
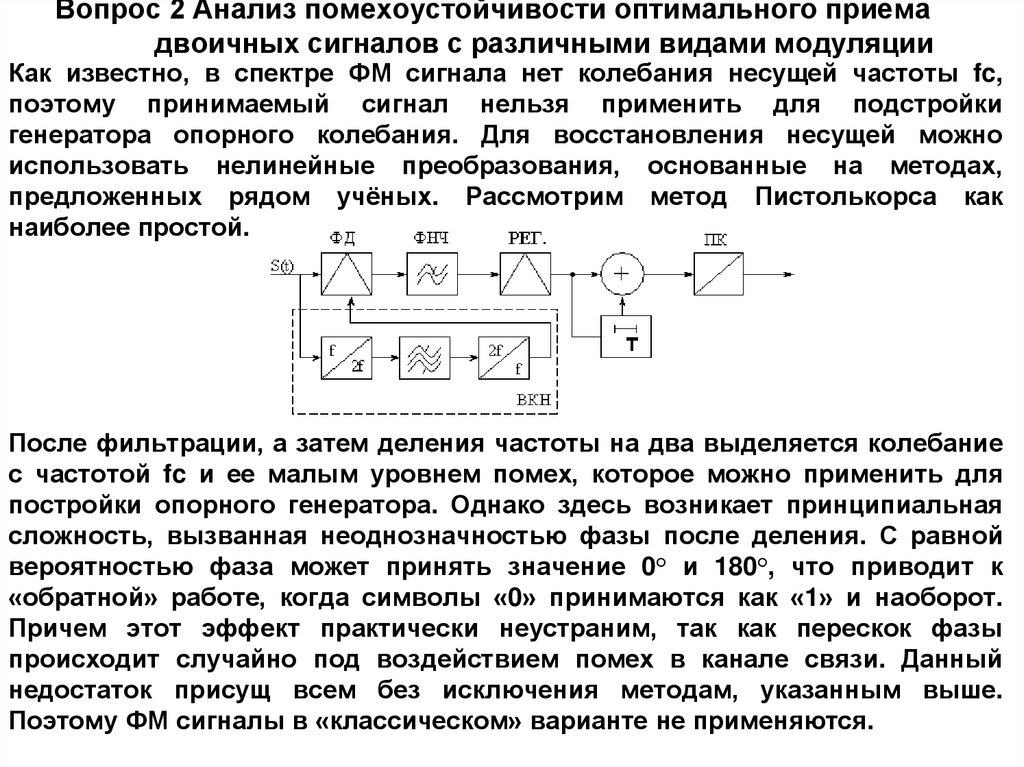
Как известно, в спектре ФМ сигнала нет колебания несущей частоты fc,
поэтому принимаемый сигнал нельзя применить для подстройки
генератора опорного колебания. Для восстановления несущей можно
использовать нелинейные преобразования, основанные на методах,
предложенных рядом учёных. Рассмотрим метод Пистолькорса как
наиболее простой.
После фильтрации, а затем деления частоты на два выделяется колебание
с частотой fc и ее малым уровнем помех, которое можно применить для
постройки опорного генератора. Однако здесь возникает принципиальная
сложность, вызванная неоднозначностью фазы после деления. С равной
вероятностью фаза может принять значение 0° и 180°, что приводит к
«обратной» работе, когда символы «0» принимаются как «1» и наоборот.
Причем этот эффект практически неустраним, так как перескок фазы
происходит случайно под воздействием помех в канале связи. Данный
недостаток присущ всем без исключения методам, указанным выше.
Поэтому ФМ сигналы в «классическом» варианте не применяются.

11.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
2.4 Сигналы с относительной фазовой манипуляцией (ОФМ)
Сигналы с ОФМ позволяют полностью устранить явление обратной
работы. В этом случае передаваемая информация вкладывается не в
абсолютное значение фазы каждой посылки сигнала, а определяются
разностью фаз последующей и предыдущей посылки. Данный способ
передачи был предложен отечественным ученым Н.Г. Петровичем и
заключается в том, что каждый символ «0» передается повторением той
реализации, которая являлась предыдущим элементом, а символ «1» изменением реализации на противоположную.
Систему ОФМ сигналов можно рассматривать как сочетание кодирования и
фазовой манипуляции. Иными словами, вначале производиться
«перекодирование» символов ак = (0,1), k = 1,2,… по правилу:
а'k = а'k-1, при аk=0 и а'k=1- а'k-1 при аk =1.
При этом посылка a0 не несет информации, выбирается произвольной и
необходима лишь для начала процесса перекодирования. После этой
операции осуществляется обычная ФМ, где в качестве управляющей
(манипулирующей) применяется перекодированная последовательность
символов а'k = (0,1), k = 0,1…
Приемник полностью известных ОФМ сигналов реализуется аналогично
оптимальному когерентному приемнику ФМ. Правда, отличие состоит в
том, что перед принятием решения о переданном сигнале производится
обратное перекодирование принимаемой последовательности

12.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
~
А а~1 , а~2 ,..., а~k ,...
В соответствии с правилом
а~ а~ а~
k
k
k 1
где - знак сложения по модулю 2.
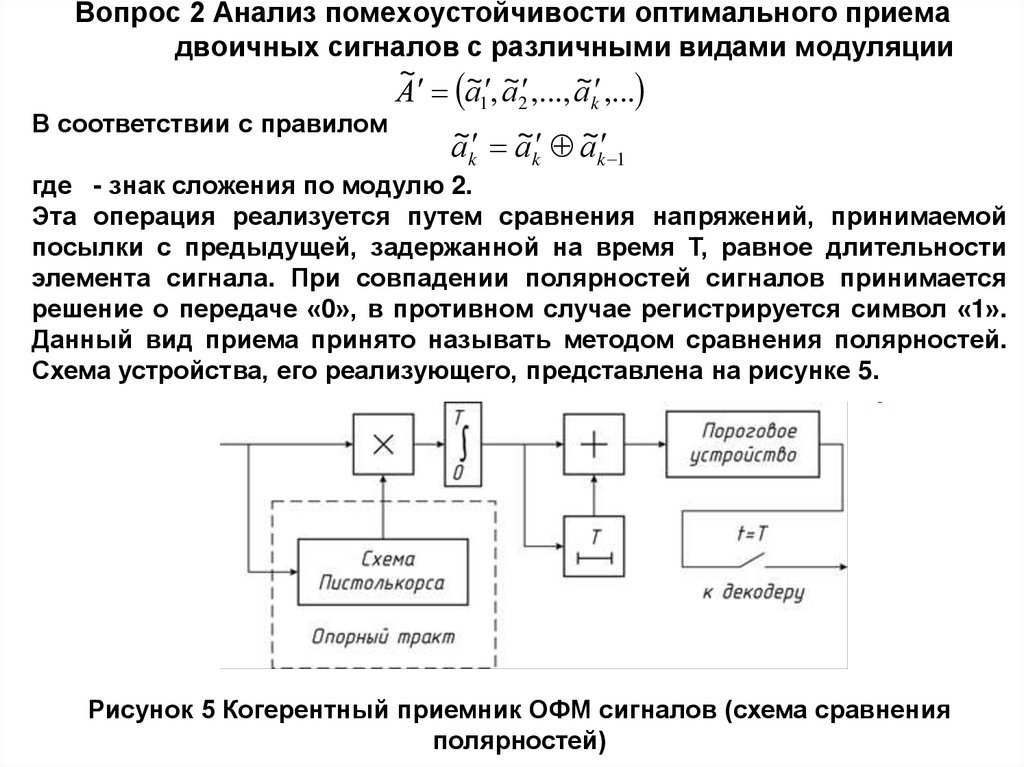
Эта операция реализуется путем сравнения напряжений, принимаемой
посылки с предыдущей, задержанной на время Т, равное длительности
элемента сигнала. При совпадении полярностей сигналов принимается
решение о передаче «0», в противном случае регистрируется символ «1».
Данный вид приема принято называть методом сравнения полярностей.
Схема устройства, его реализующего, представлена на рисунке 5.
Рисунок 5 Когерентный приемник ОФМ сигналов (схема сравнения
полярностей)

13.

Вопрос 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
Опорный тракт обычно выполняется по схеме Пистолькорса с делением,
фильтрацией и умножением частоты на два. При этом в отличие от ФМ в
данном случае скачок фазы не опасен, ошибочно будет зарегистрирован
лишь один элемент, а остальные принимаются верно, при условии, что в
канале отсутствуют помехи. Сказанное иллюстрируется таблицей 1, где для
сравнения показан также принцип ФМ.
Таблица 1
ОФМ
ФМ
Информация аk
0111001010
0111001010
Перекодированные
00101110011
посылки а'k
Фаза сигнала
↑↑↓↑↓↓↓↑↑↓↓
↑↓↓↓↑↑↓↑↓↑
*
*
Фаза на приеме
↑↑↓↑↑↑↑↓↓↑↑
↑↓↓↑↓↓↑↓↑↓
Принятые посылки аk 0110001010
0110110101
Изменение фазы обозначается стрелками, при этом стрелка, направленная
вверх, соответствует фазе 0°, стрелка, направленная вниз фазе 180°.
Звездочкой на рисунке обозначен момент перескока фазы, начиная с
которого прием ФМ сигнала производится с ошибками («обратная работа»).
В отличие от этого только один символ ОФМ сигнала принимается неверно,
а остальные - безошибочно.

14.

ВОПРОС 2 Анализ помехоустойчивости оптимального приема
двоичных сигналов с различными видами модуляции
Оценим потенциальную помехоустойчивость когерентного приемника ОФМ
сигналов в условиях аддитивного белого шума. Ошибка в приеме возникает при
условии, что k-я посылка принята неверно, а (k-1)-я – правильно, либо наоборот.
Поскольку в рассматриваемом случае ошибки возникают независимо, вероятность
каждого из сочетаний этих событий равна РФМ(1- РФМ) , где РФМ – вероятность
ошибочного приема ФМ сигналов. Окончательно вероятность ошибки приема ОФМ
сигналов имеет вид
2h F 2h 2P
PОФМ 2 PФМ (1 PФМ ) 2 1 F
2
2
ФМ
Данная величина оказывается примерно вдвое больше, чем вероятность ошибки
для ФМ сигналов. Однако это и есть необходимая «плата» за возможность
устранения случайных перескоков в фазы в канале, приводящих к появлению
обратной работы.

15.

КОНТРОЛЬНЫЕ ВОПРОСЫ
1.
2.
3.
4.
5.
6.
7.
Поясните, чем определяется помехоустойчивость оптимального
когерентного приема двоичных сигналов в условиях белого шума
Запишите выражения для определения вероятности ошибочного
приема АМ сигналов
Запишите выражения для определения вероятности ошибочного
приема ЧМ сигналов
Запишите выражения для определения вероятности ошибочного
приема ФМ сигналов
Докажите,
что
помехоустойчивость
приема
ФМ
сигналов
максимальна
Поясните принцип образования сигналов с ОФМ
Дайте оценку помехоустойчивости приема ОФМ сигналов при
наличии белого шума