Разработка моделей. Лекция 9

1.

Разработка
модели
Лекция 9
Преподаватель: Сатыбалдиева Рысхан
Жакановна, к.техн.наук, ассоц.проф.
r.satybaldiyeva@satbayev.university

2.

Содержание
• Линейная регрессия и множественная линейная регрессия
• Оценка моделей с помощью визуализации

3.

Модель
• математическое уравнение, используемое для прогнозирования
значения, заданного одним или несколькими другими
значениями.
• Соотношение одной или нескольких независимых переменных
или объектов к зависимым переменным.
• Например,
• возьмем в качестве независимой переменной или
объекта пробег модели автомобиля на галлон,
• выходным значением модели или зависимой переменной
является цена.

4.

Релевантность данных
• чем более релевантные данные, тем точнее модель.
• Чтобы понять, почему важно больше данных, рассмотрим следующую
ситуацию.
У вас две почти одинаковые машины.
• Розовые автомобили продаются за значительно меньше.
• Вы хотите использовать свою модель, чтобы определить цену двух
автомобилей, один розовый, один красный.
• Если ваши модели независимые переменные или функции не включают
цвет, ваша модель будет предсказывать ту же цену для автомобилей,
которые могут продавать гораздо меньше.
• В дополнение к получению большего количества данных, вы можете
попробовать различные типы моделей.

5.

Регрессия
• Регрессия ищет отношения между переменными.
Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит
от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и
так далее.
• Регрессия решает проблему единого представления данных анализа
для каждого работника. Причём опыт, образование, роль и город – это
независимые переменные при зависимой от них зарплате.
• Регрессия полезна для прогнозирования ответа на новые условия.
Можно угадать потребление электроэнергии в жилом доме из данных
температуры, времени суток и количества жильцов.

6.

Переменные
Линейная регрессия оценивает коэффициенты линейного
уравнения, содержащего одну или несколько независимых
переменных, позволяющие наилучшим образом предсказать
значение зависимой переменной. Например, вы можете
попытаться предсказать объем годовых продаж для сотрудника
отдела продаж (зависимая переменная) по таким независимым
переменным, как возраст, образование и стаж работы.
• Регрессия помогает найти функцию, которая отображает
зависимость одних переменных или данных от других.

7.

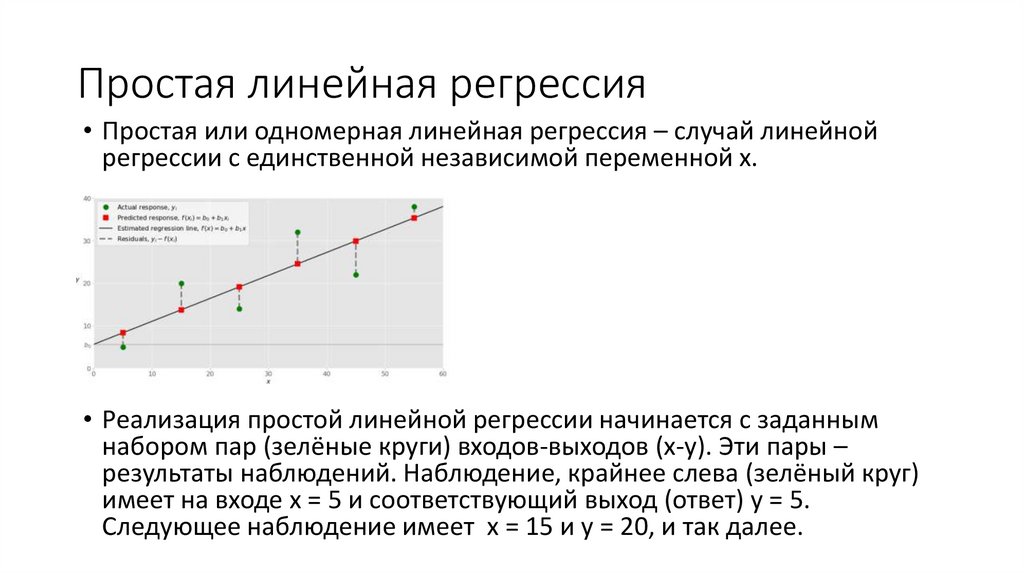
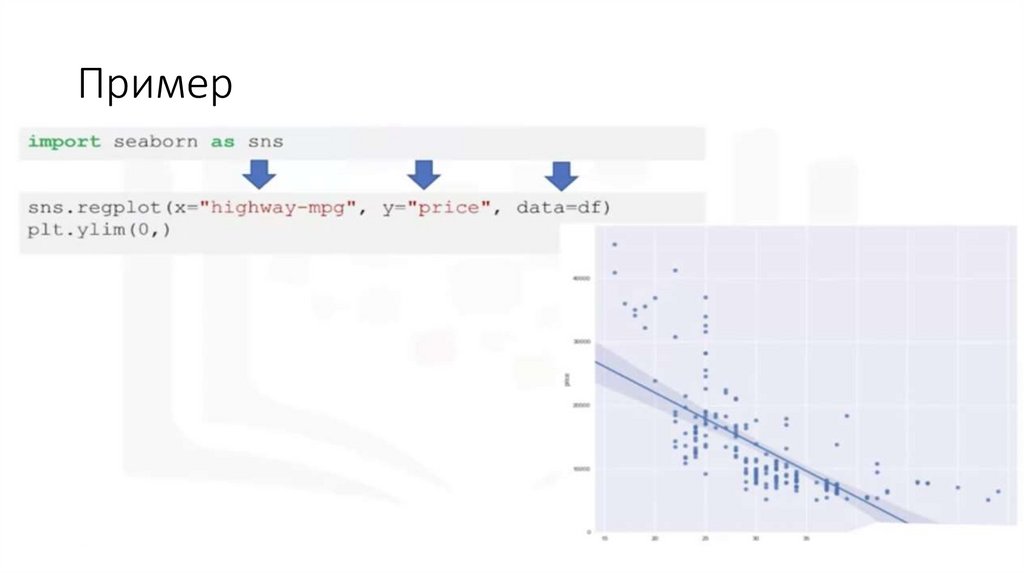
Простая линейная регрессия
• Простая или одномерная линейная регрессия – случай линейной
регрессии с единственной независимой переменной x.
• Реализация простой линейной регрессии начинается с заданным
набором пар (зелёные круги) входов-выходов (x-y). Эти пары –
результаты наблюдений. Наблюдение, крайнее слева (зелёный круг)
имеет на входе x = 5 и соответствующий выход (ответ) y = 5.
Следующее наблюдение имеет x = 15 и y = 20, и так далее.

8.

Простая линейная регрессия:
• Y