Похожие презентации:
Основні поняття стереометрії. Аксіоми стереометрії та наслідки з них
1.
МатематикаАрифметик
а
Числа і дії
над ними,
відношенн
я між
числами
Алгебра і
початки
аналізу
Функції, їх
властивос
ті і графіки
Рівняння,
нерівності,
задачі,
перетворення
виразів.
Геометрія
Планіметрі
я
Фігури на
площині
та їх
властивос
ті
Стереометрія
Фігури у
просторі та
їх
властивості.
2.
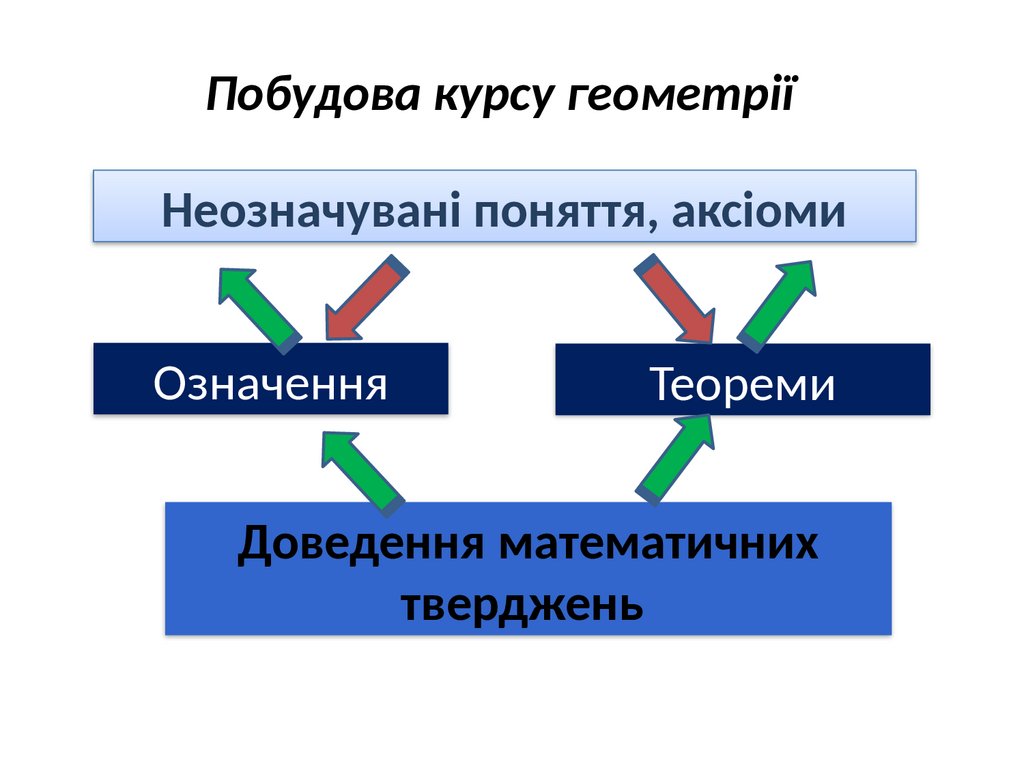
Побудова курсу геометріїНеозначувані поняття, аксіоми
Означення
Теореми
Доведення математичних
тверджень
3.
Тема:Основні поняття
стереометрії. Аксіоми
стереометрії та наслідки з
них.
4.
Основні поняття геометріїГеометричною фігурою
називають будь-яку множину точок.
Точка, пряма, площина –
неозначувані поняття геометрії.
5.
Точки позначають великими латинськими буквами.A, B, C, D, E, F, K, L, M, N, O, P, R, S, T
М
А
F
Прямі позначають малою
латинською буквою, або двома
великими латинськими буквами.
a, b, c, d, m, n, p
p
С
D
6.
Площини позначають грецькими буквами.α, β, γ, φ, ω
На малюнках площини зображують:
α
β
γ
7.
Користуються математичними висловленнями:Точка А лежить у площині φ.
Площина φ проходить
через точку А.
А
φ
А φ
а
ω
Пряма а лежить у площині ω.
Площина ω проходить через пряму а.
а ω
Пряма а включається в площину ω.
Площина ω містить пряму а.
8.
Властивості понять розкривають за допомогоюпевних тверджень.
У справедливості математичних тверджень
переконуються за допомогою доведень.
Твердження, які доводять, називають теоремами.
Перші твердження приймають без доведення,
їх називають аксіомами.
9.
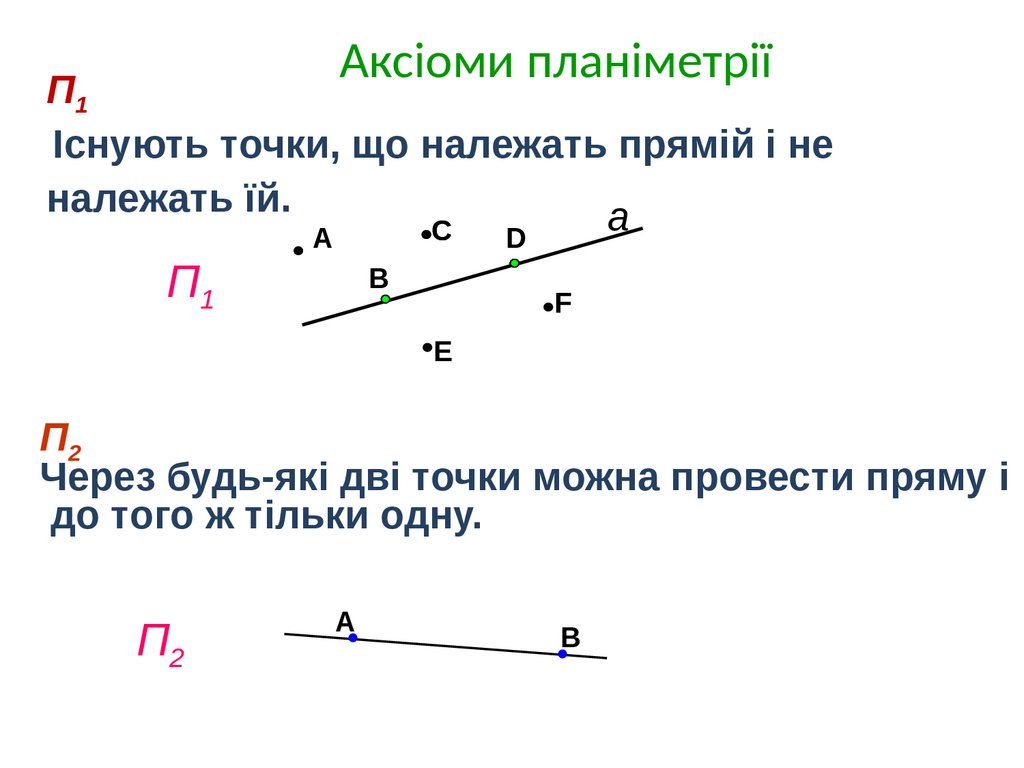
Аксіоми планіметріїП1
Існують точки, що належать прямій і не
належать їй.
а
П1
C
A
B
D
F
E
П2
Через будь-які дві точки можна провести пряму і
до того ж тільки одну.
П2
А
В
















 Математика
Математика








