Аксіоми стереометрії і наслідки з них

1.

2.

План
1. Стереометрія. Основні фігури у
просторі.
2. Аксіоми стереометрії.
3. Наслідки із аксіом.
4. Розв'язування задач.

3.

Геометрія
Планіметрія
Стереометрія
Планіметрія – це розділ
геометрії, в якому
вивчаються фігури на
площині.
Стереометрія – це розділ
геометрії, в якому
вивчаються фігури в
просторі.

4.

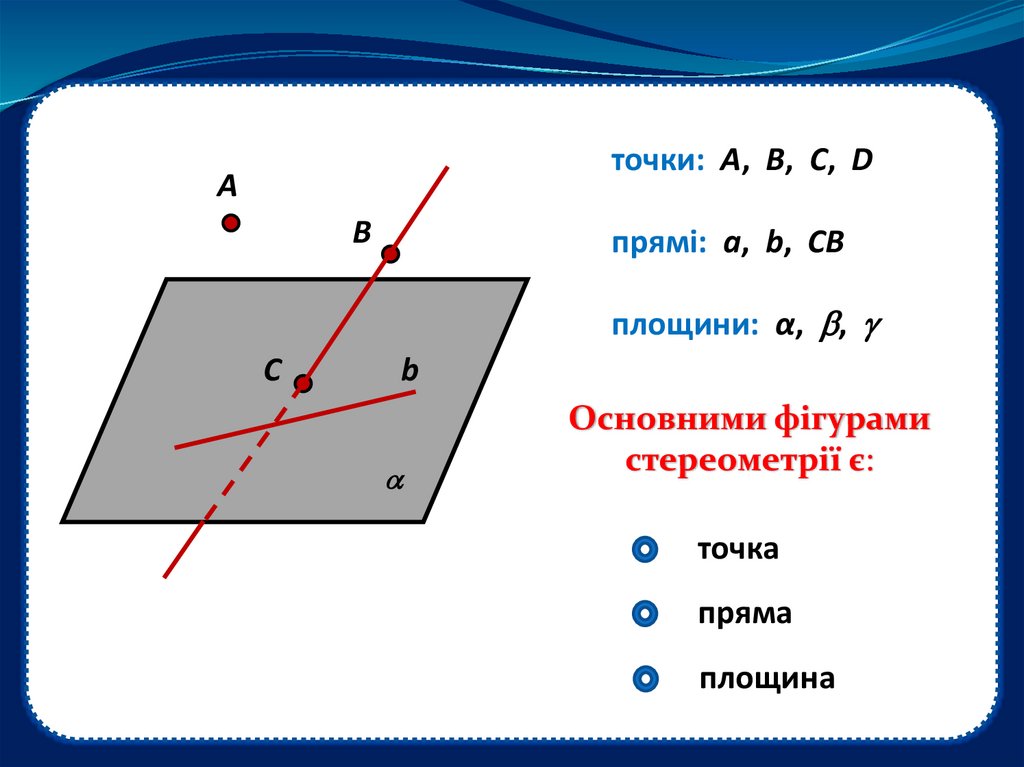
точки: A, B, C, D
A
B
прямі: a, b, CB
площини: α, ,
C
b
Основними фігурами
стереометрії є:
точка
пряма
площина

5.

Точка і пряма – це основні фігури планіметрії, тому в
стереометрії справедливі аксіоми планіметрії.
1. Яка б не була пряма, існують точки, що належать цій
прямій , і точки що їй не належать.
2. Через будь які дві точки можна провести пряму, і тільки
одну.

6.

Аксіоми стереометрії (С) – це основні властивості площин
у просторі.
С1. Яка б не була площина, існують точки, що
належать цій площині, і точки що їй не належать
C
А α
A
В α
B
С α

7.

С2. Якщо дві різні площини мають спільну точку, то вони
перетинаються по прямій, яка проходить через цю точку.
A
a
А α, А
α =а
А а

8.

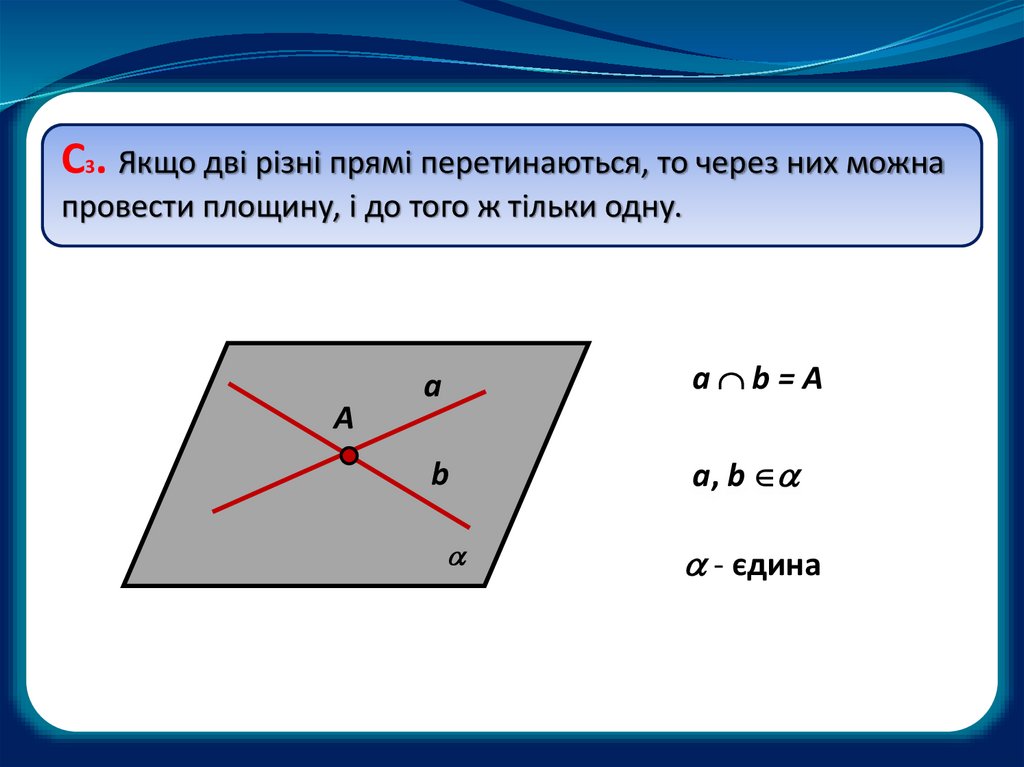
С3. Якщо дві різні прямі перетинаються, то через них можна
провести площину, і до того ж тільки одну.
A
а
a b=A
b
a, b
- єдина

9.

С4. Якщо дві точки прямої належать площині,
то і вся пряма належить цій площині.
а
B
A
А , В ,
А а, B a,
то а

10.

Теорема. Через пряму і точку, що не лежить на ній,
можна провести площину , і до того ж тільки одну.
A
1
а
В
Дано: A a
Довести: A ; а
- єдина
Доведення:
1. В а, АВ а = В ;
2. АВ , а (акс. С 3 ) ;
3. припустимо існує 1 така , що А 1 , а 1 ;
4. 1 = b (акс. С2), А, В b, A a – суперечить умові,
- єдина.

11.

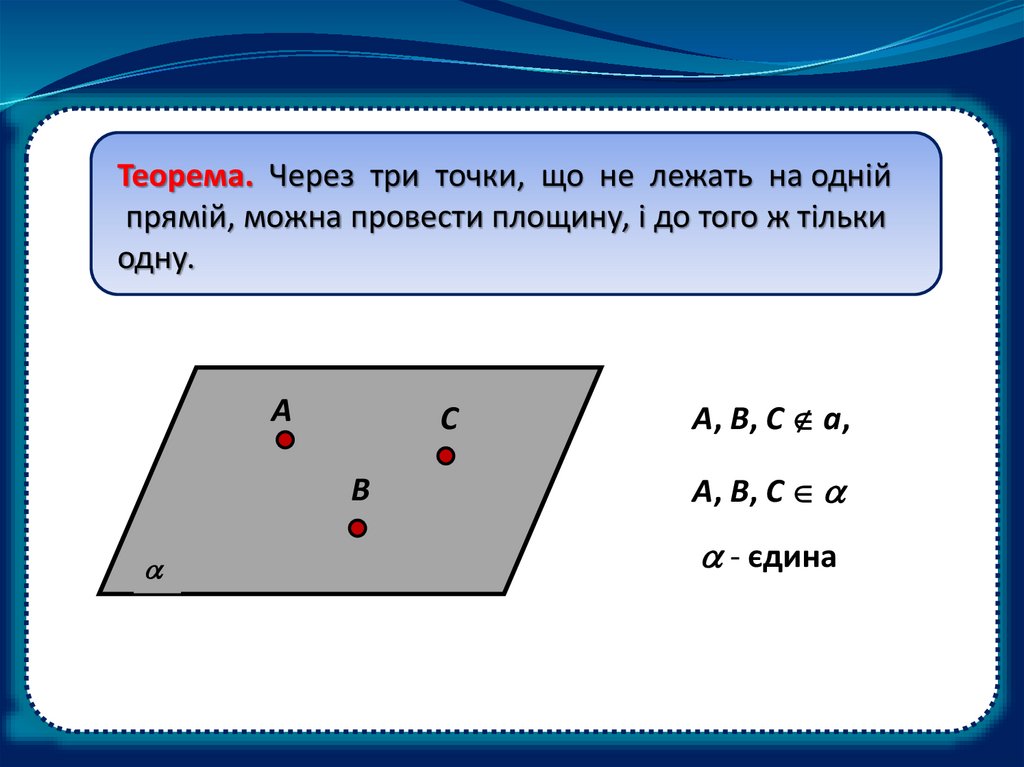
Теорема. Через три точки, що не лежать на одній
прямій, можна провести площину, і до того ж тільки
одну.
A
C
B
A, B, C a,
A, B, C
- єдина

12.

Розв’язування задач
№ 1. Дано: три точки A, B, C ;
АВ = 5см, ВС = 7см, АС = 12см.
Скільки площин можна через них провести?
C
B
A
а
АВ + ВС = АС
А, В, С а

13.

№ 2. Виконання усних вправ
1. Чи правильно, що:
1) існують хоча б три точки, що не лежать на одній прямій;
2) у кожній площині лежить хоча б одна точка;
3) якщо дві площини мають спільну точку, то вони мають ще
хоча б одну спільну точку;
4) існують хоча б чотири точки, що не лежать на одній
площині?
2. Які з тверджень правильні:
1) будь - які дві точки завжди лежать на одній прямій;
2) будь – які три точки завжди лежать на одній прямій;
3) будь – які три точки завжди лежать в одній площині;
4) будь – які чотири точки завжди лежать в одній площині.

14.

№ 3.
Чи належить точка К площині
паралелограма ABCD, якщо точка N належить
відрізку AD, а точка М – відрізку ВС.
K
B
A
N
M
C
D