Общие сведения о кривых линиях и поверхностях

1.

ОБЩИЕ
СВЕДЕНИЯ О
КРИВЫХ ЛИНИЯХ
И ПОВЕРХНОСТЯХ

2.

Кривая линия - совокупность последовательных
положений движущейся точки, а также как линия
пересечения поверхностей.
Закономерная кривая – если при своем
образовании она подчинена какому-либо
геометрическому закону.
Если этот закон можно описать алгебраическим
уравнением, то кривая называется алгебраической, в
противном случае – трансцендентной.
Алгебраические кривые определяются своим
порядком – количеством пересечений с прямой.

3.

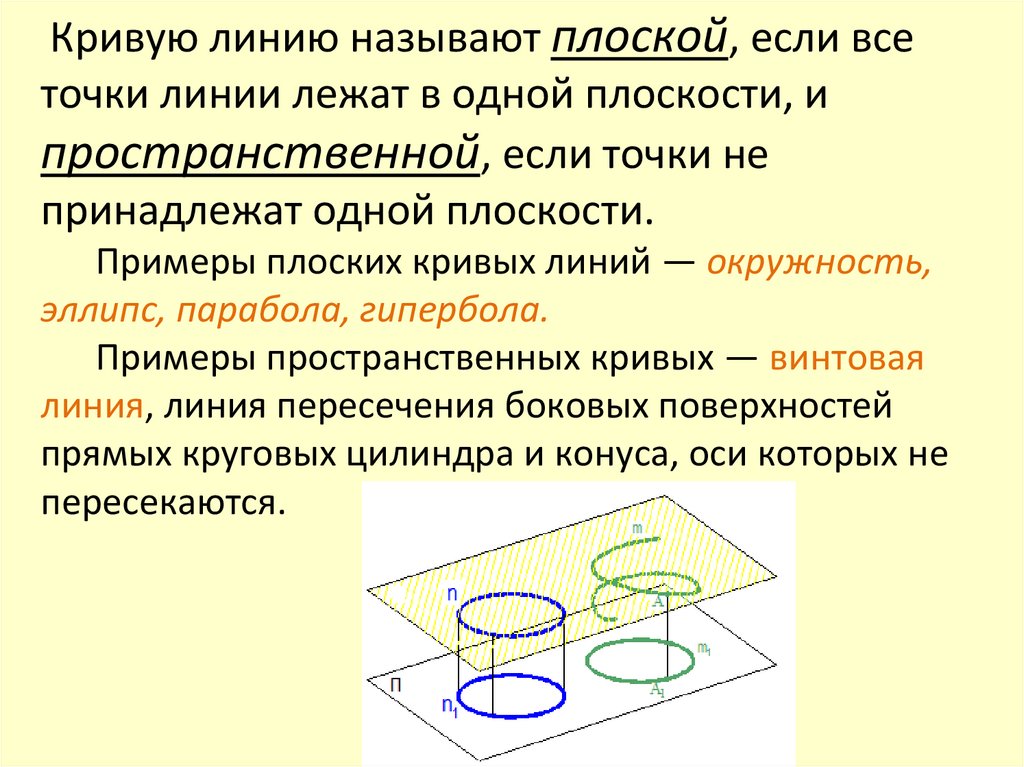
Кривую линию называют плоской, если все
точки линии лежат в одной плоскости, и
пространственной, если точки не
принадлежат одной плоскости.
Примеры плоских кривых линий — окружность,
эллипс, парабола, гипербола.
Примеры пространственных кривых — винтовая
линия, линия пересечения боковых поверхностей
прямых круговых цилиндра и конуса, оси которых не
пересекаются.

4.

Свойства проецирования кривых
• Проекция кривой n-го порядка
является кривой порядка не выше n.
• Касательная к кривой в общем случае
проецируется в виде касательной к
проекции кривой.
• Особые точки плоской кривой в общем
случае проецируются в особые точки
ее проекции.

5.

Поверхность
– это совокупность всех
последовательных положений
некоторой перемещающейся в
пространстве линии

6.

Способы образования и задания
поверхностей.
Каркас поверхности.
Определитель поверхности

7.

Существуют три способа задания поверхностей:
1. Аналитический - при помощи уравнений;
2. При помощи каркаса (Каркас поверхности это упорядоченное множество точек или
линий, принадлежащих поверхности);
3. Кинематический, т. е. перемещением линий
в пространстве.

8.

В начертательной геометрии поверхность задают
кинематически - как множество всех положений
перемещающейся по определенному закону линии
в пространстве.
Движущаяся в процессе образования
поверхности линия называется
образующей
Линия, по которой скользит образующая,
называется направляющей

9.

l n-k
l
l
n
m
l
n
C

10.

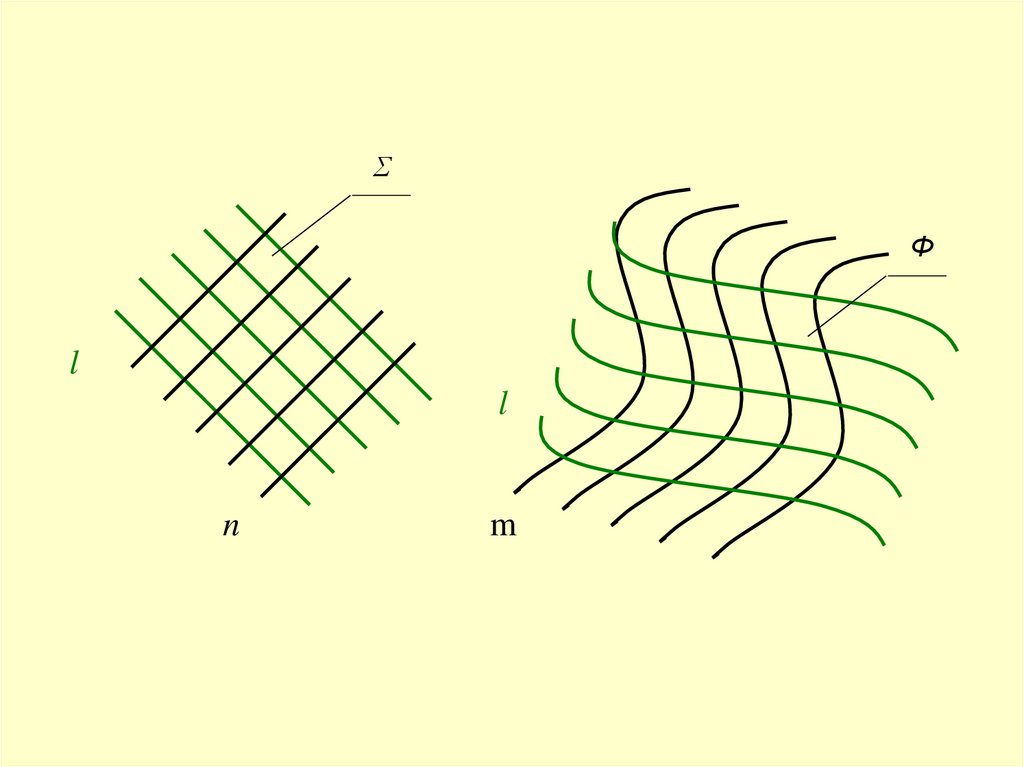
Совокупность намеченных на поверхности
образующих и направляющих линий
называется линейным каркасом
поверхности

11.

Σ
Φ
l
l
n
m

12.

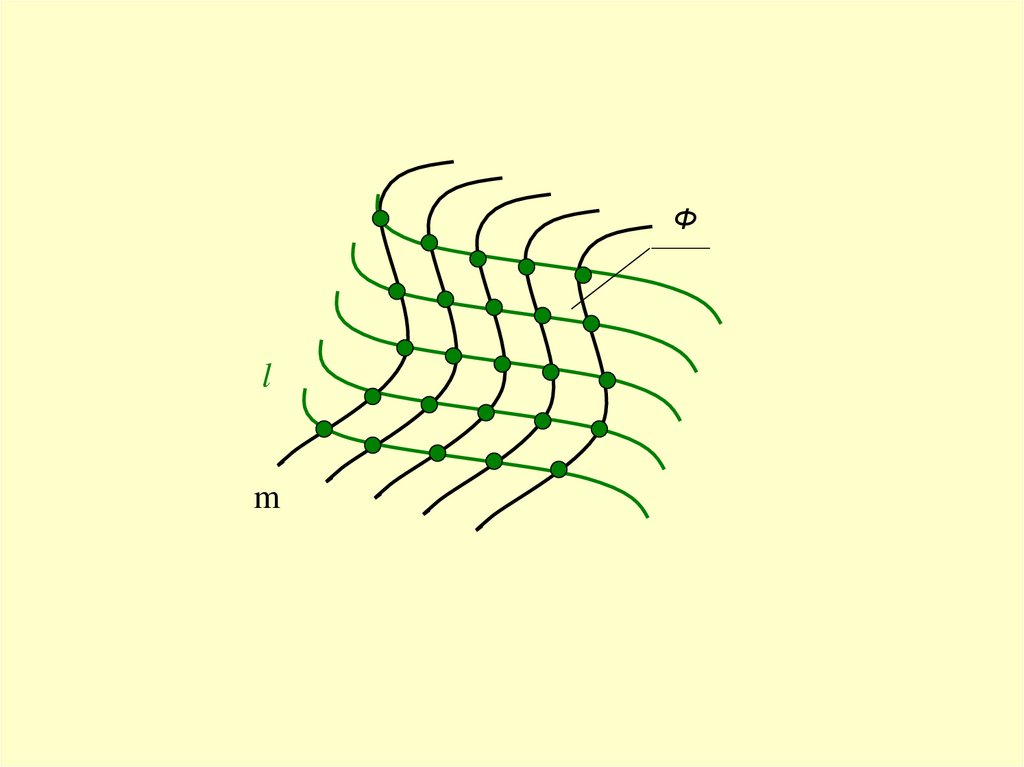
Совокупность точек на поверхности,
выбранных таким образом, чтобы,
ориентируясь по ним, можно достаточно
полно представить форму поверхности,
называется точечным каркасом
поверхности

13.

Φ
l
m

14.

Одна и та же поверхность может быть образована различными
способами
i
l
i
l
c
цилиндр образован вращением прямой образующей L
вокруг неподвижной оси i
образующая - окружность с центром на оси цилиндра

15.

Совокупность независимых условий,
однозначно задающих поверхность,
называется её
определителем
Ф(Г)[A]
Г – геометрическая часть
А – алгоритмическая часть
Геометрическая часть - совокупность геометрических фигур,
с помощью которых можно образовать поверхность.
Алгоритмическая часть - алгоритм формирования
поверхности при помощи фигур, входящих в
геометрическую часть определителя.

16.

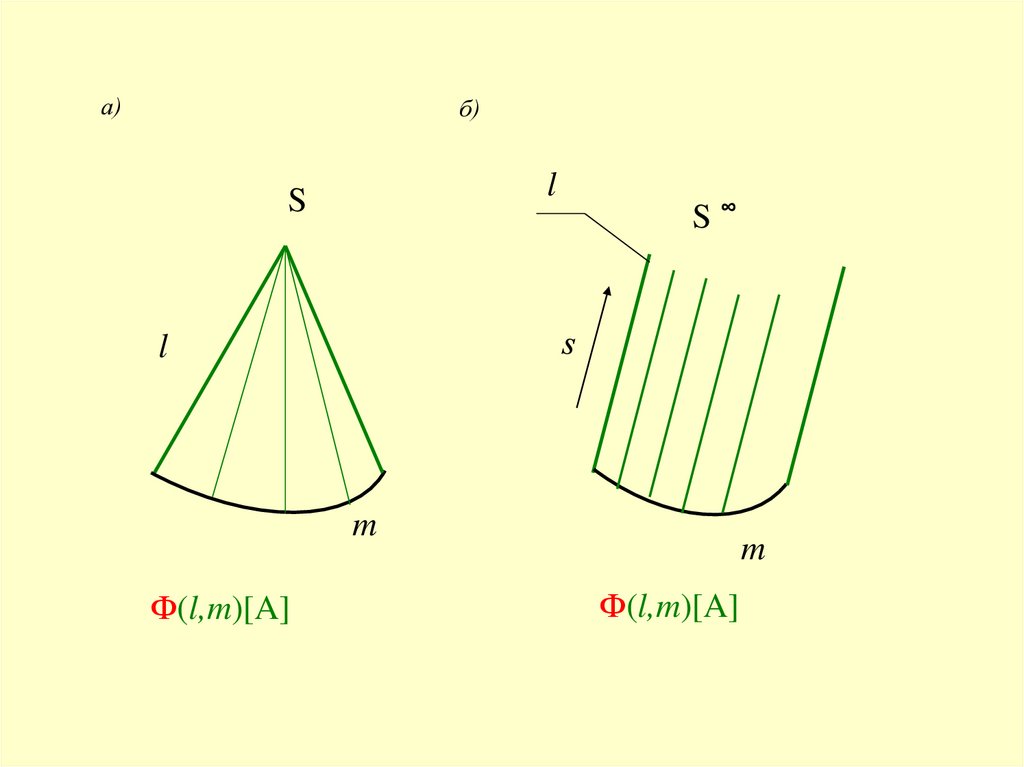
а)
б)
l
S
S∞
l
m
Ф(l,m)[A]
m
Ф(l,m)[A]

17.

Очерк поверхности
при ортогональном проецировании – это
линия, ограничивающая проекцию
поверхности на плоскостях проекций

18.

Фронтальный очерк
П2
х
П1
Горизонтальный очерк

19.

Очерк проекции поверхности является проекцией
соответствующей линии видимого контура.
Линия видимого контура поверхности разделяет ее на
две части − видимую, обращенную к наблюдателю, и
невидимую. Никакая точка поверхности не может
спроецироваться за пределы очерка.

20.

Классификация
поверхностей

21.

1. По виду образующей все поверхности можно
разделить на
линейчатые
и
нелинейчатые
У линейчатых поверхностей образующей является
прямая линия,
у нелинейчатых – кривая линия

22.

2. Поверхности закономерные и
незакономерные.
Если образующая поверхности движется по
определенному закону, то поверхность называется
закономерной или правильной, в противном
случае поверхность называется незакономерной.

23.

3. Поверхности развертывающиеся и
неразвертывающиеся.
Развертывающиеся поверхности – поверхности,
которые после разреза их по образующей могут быть
односторонне совмещены с плоскостью без наличия
разрывов и складок.
Неразвертывающиеся поверхности – поверхности,
которые не могут быть совмещены с плоскостью без
наличия разрывов и складок.

24.

4. Поверхности с образующей постоянной и
переменной формой.

25.

5. Поверхности с поступательным,
вращательным или винтовым движением
образующей.

26.

Линейчатые
поверхности

27.

Рассмотрим основные
виды линейчатых
поверхностей

28.

ГРАННЫЕ ПОВЕРХНОСТИ
l
S- вершина
Ребро
l
А
Грань
m
В
С
А
В m С

29.

Гранные – поверхности, образованные
перемещением прямолинейной образующей
по ломанной линии.
Отсеки плоскостей, образующие
многогранную поверхность, называются
гранями, линии пересечения смежных граней
- ребрами, точки пересечения не менее чем
трех граней - вершинами.

30.

Пирамидальная
поверхность
Призматическая
поверхность
S
А
l
А
l
s
m
m
Линейчатая
поверхность,
образованная перемещением
прямой линии, проходящей
через фиксированную точку S
(вершину),
по
ломанной
направляющей m
Линейчатая поверхность, образованная
перемещением прямой линии,
движущейся параллельно некоторому
заданному направлению s и
пересекающей направляющую m, которая
представляет собой ломаную линию.

31.

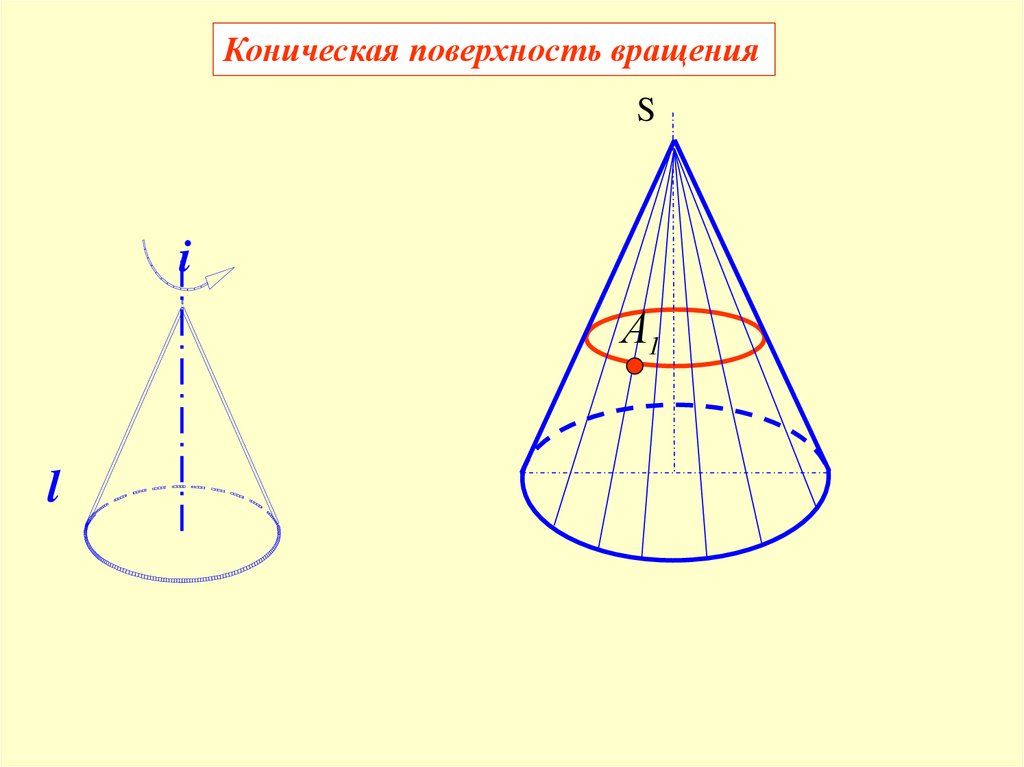
Коническая поверхность –поверхность, образованная вращением
прямолинейной образующей вокруг оси, при
этом, образующая пересекает ось в собственной
точке.
Цилиндрическая поверхность
S
l
поверхность, образованная движением прямолинейной
образующей по кривой направляющей m, при этом
образующая l во всех положениях параллельна
некоторому заданному направлению.
А
l
А
s
m
m

32.

Точка принадлежит поверхности,
если она лежит на какой – нибудь
линии этой поверхности
Линия
принадлежит поверхности,
если все ее точки принадлежат этой
поверхности

33.

S2
А2
М2
m2
m1
М1
А1
S1

34.

Алгоритм
построения недостающей проекции точки,
принадлежащей линейчатой поверхности
1. Через заданную проекцию точки, лежащей на
поверхности, проводится проекция простейшей линии,
принадлежащей этой поверхности
2. Строится вторая проекция этой линии
из условия ее принадлежности данной поверхности
3. По линии проекционной связи на построенной
проекции линии находится искомая проекция заданной
точки

35.

S2
S
Ф
l
l2
А
A2
m2
m
x
m1
l1
A1
S1

36.

s2
s
l
l
2
A
Ф
2
m
A
2
x
m
m
A
s1
l1
1
1

37.

l2 S2
S
Ф
l
A2
A
m
m2
x
m1
A1
l1
S
1

38.

S
А
l
s2
Ф
2
l
m
A2
m2
x
m1
A1
s1
l
1

39.

Таким образом,
через каждую точку линейчатой
поверхности можно всегда провести
прямую линию

40.

Поверхности
вращения

41.

Поверхности вращения – поверхности,
образованные вращением линии (образующей)
вокруг прямой – оси вращения.
Поверхности вращения могут быть
линейчатыми и нелинейчатыми.
У поверхности вращения
геометрическая часть определителя состоит из
образующей l и оси вращения i:
Ф (l,i)[A]

42.

Плоскости, перпендикулярные к оси
вращения, пересекают поверхность по
окружностям, которые называются
параллелями
Радиус каждой параллели измеряется
от оси до очерка
от оси до очерка !!!

43.

Наибольшую из параллелей называют
экватором,
наименьшую –
горлом

44.

Плоскость, проходящая через ось
поверхности вращения, называется
меридиональной,
а линия пересечения поверхности с этой
плоскостью называется
меридианом поверхности.
Если эта плоскость параллельна фронтальной
плоскости проекций П2,
то в сечении получается меридиан, который
называется главным меридианом

45.

Поверхность вращения
i
ÏПараллель
àðàëëåëü
Горло
Ãî ðëî
Главный
меридиан
Ãë.
ì åðèäèàí
Экватор
Ýêâàòî
ð
Меридиан
Ì åðèäèàí

46.

Примеры поверхностей
вращения

47.

i
Сфера
параллель
главный меридиан
l
A
меридианы
экватор

48.

Коническая поверхность вращения
S
i
А1
l

49.

Цилиндрическая поверхность вращения
i
l
А1

50.

R A2
A1

51.

Алгоритм
решения задач на принадлежность точки поверхности
вращения
1. Через заданную проекцию точки проводят
проекцию вспомогательной параллели
2. Строят вторую проекцию этой параллели, измеряя ее радиус от
оси вращения до очерка поверхности
от оси до очерка !!!
3. По линии проекционной связи на построенной
проекции параллели находят недостающую проекцию
точки с учетом ее видимости

52.

Построение точки
на поверхности
сферы

53.

А2
(А3)
R
R
А1

54.

55.

Построение точки
на поверхности прямого
кругового конуса

56.

S2
А
А2
S1
А1

57.

А2
(В2)
А
В1
А1
А3
В3

58.

Построение точки
на поверхности прямого
кругового цилиндра

59.

А
А2
А
(В2)
В1
А
1
(В3)
3

60.

Винтовые поверхности

61.

Все точки винтовой поверхности совершают
винтовые движения, описывая
винтовые линии – гелисы,
а поверхности называются
геликоидами

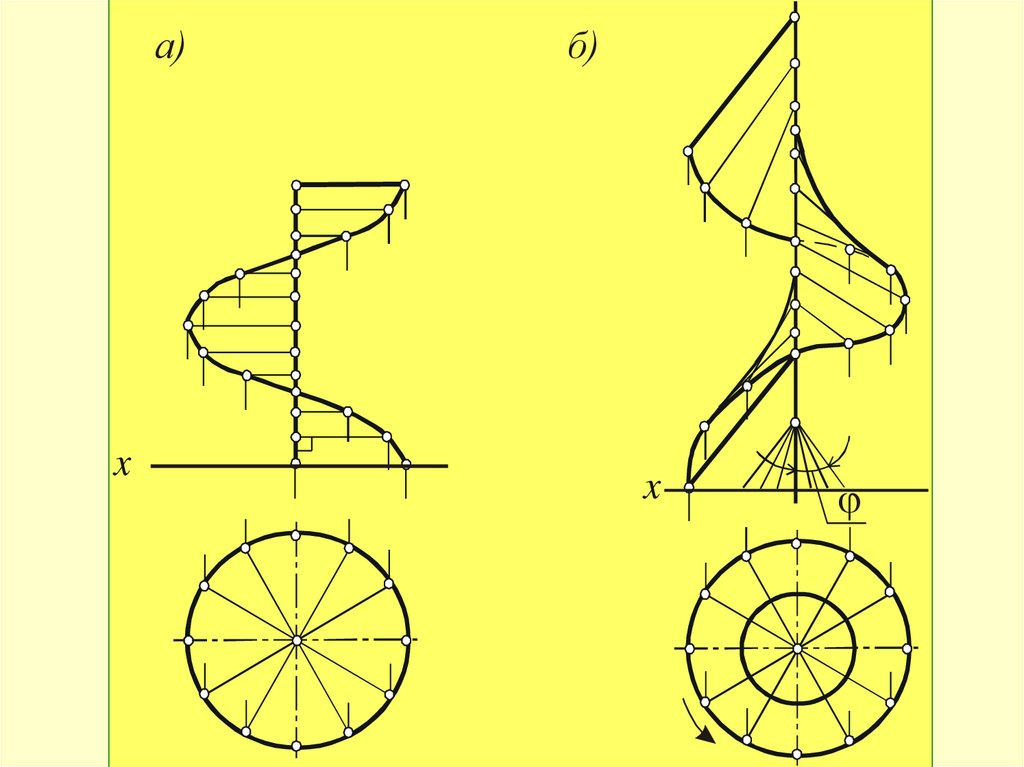
62.

Прямые геликоиды,
если угол наклона образующей
равен 90
Наклонные - если угол
не равен 90

63.

а)
x
б)
x

64.

Выводы:
- поверхность может быть получена вращением некоторой
образующей вокруг оси или движением ее по направляющей
- поверхность может быть задана на чертеже проекциями элементов
геометрической части ее определителя или
для достижения большей наглядности – очерком
- поверхности могут быть систематизированы в зависимости от вида
образующих и направляющих, а также от закона движения образующих
- для нахождения недостающей проекции точки, лежащей на
поверхности, пользуются характерными для данной поверхности
простейшими линиями

65.

1. Пересечение
поверхности плоскостью
2. Конические сечения

66.

Характерные и случайные точки линии
пересечения поверхностей
1. Характерные (или опорные). Точки, которые
выделяются среди множества других своим особым
положением на поверхностях и относительно плоскостей
проекций. Таких точек в каждой конкретной задаче всегда
конечное число.
2. Случайные (или промежуточные) – точки
расположенные между характерными точками.
При построении линии пересечения поверхностей сначала
определяют, если это возможно, характерные точки, а затем находят
промежуточные точки, количество и плотность которых зависит от
кривизны проекций линии пересечения, масштаба чертежа и
требуемой точности

67.

Конические сечения
прямые
эллипс
гипербола
окружность
парабола
67

68.

Прямые, окружность, эллипс
68

69.

Парабола
69

70.

Гипербола