Похожие презентации:
Численное интегрирование
1.
Российский государственный университетнефти и газа
им. И.М. Губкина
Кафедра «Информатики»
Лекция
1
2.
Постановка задачи:вычислить интеграл вида
b
I f ( x )dx ,
a
где a и b – пределы интегрирования;
f(x) – непрерывная функция на отрезке [a,b]
2
3.
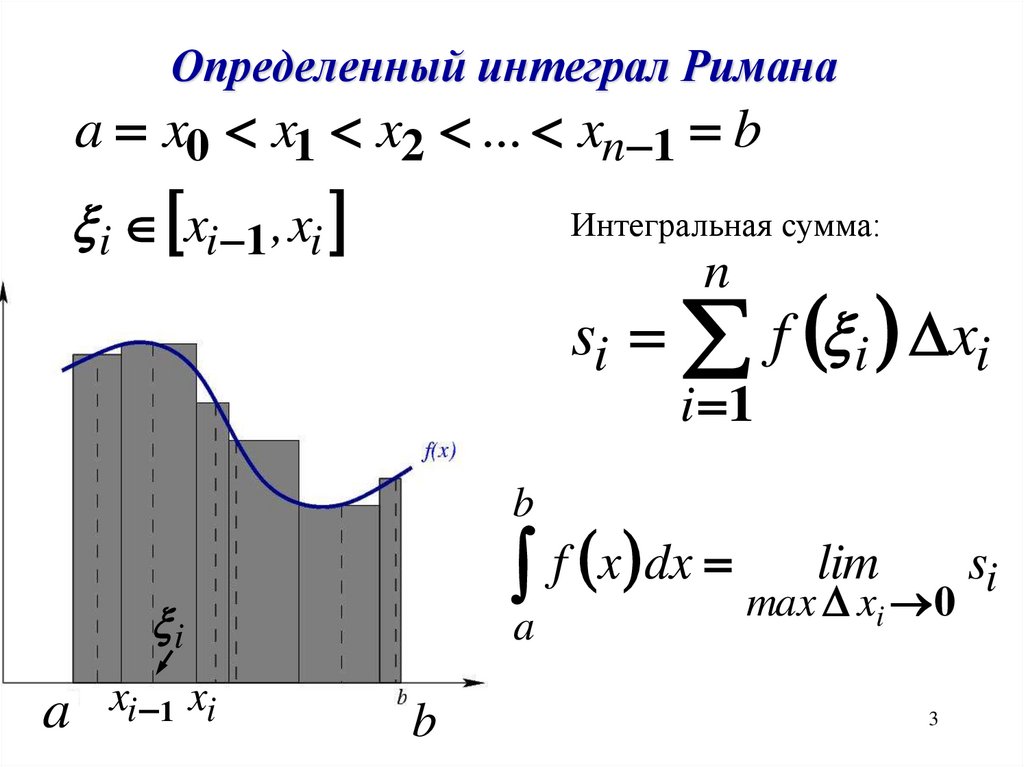
Определенный интеграл Риманаa x0 x1 x2 ... xn 1 b
i xi 1 , xi
Интегральная сумма:
n
si f i xi
i 1
b
si
f x dx maxlim
x 0
i xi 1 , xi
i
a
xi 1 xi
a
b
i
3
4.
Вычисление определенных интеграловb
b
f x dx F x a F b F a
a
Значение определенного интеграла можно трактовать
как площадь криволинейной трапеции
4
5.
методы численного интегрированияприменяют
Если:
1) вид функции f(x) не допускает
непосредственного интегрирования;
2) значения функции f(x) заданы в виде таблицы
Основная идея - замена подынтегральной
функции на более простую, интеграл от
которой легко вычисляется аналитически.
5
6.
Квадратурные формулыНьютона-Котеса
Замена f(x) – на полином различных
степеней.
f(x)=const - метод прямоугольников,
f(x)=kx+b - метод трапеций,
f(x)=ax2+bx+c - метод Симпсона.
6
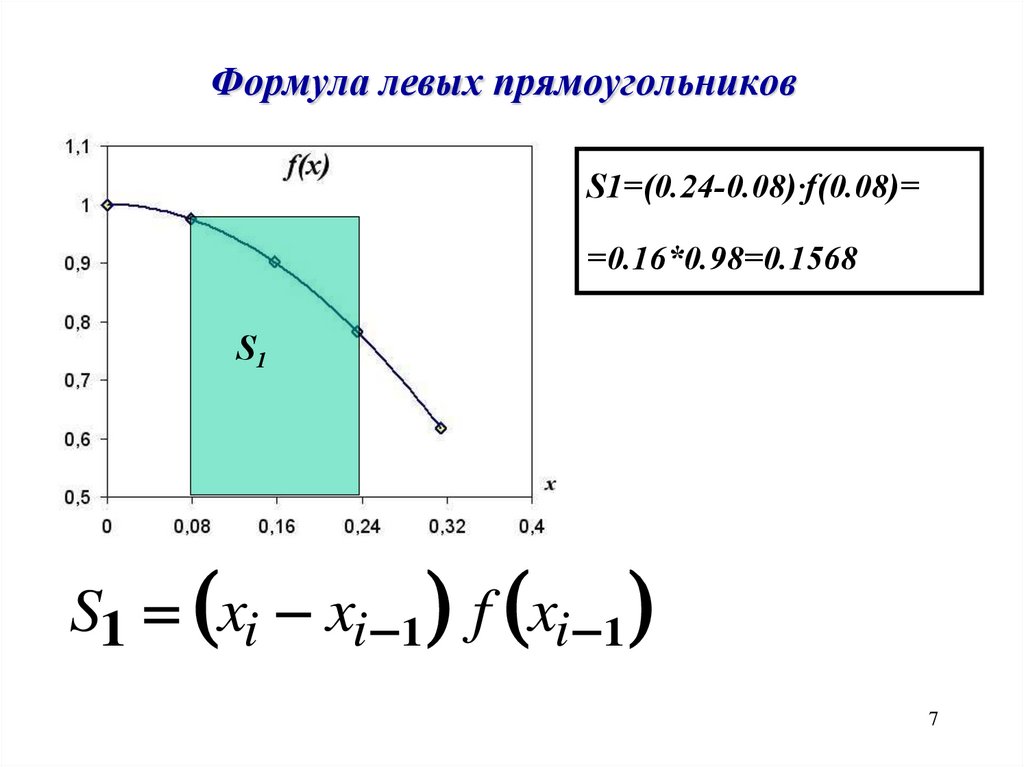
7.
Формула левых прямоугольниковS1=(0.24-0.08)·f(0.08)=
=0.16*0.98=0.1568
S1
S1 xi xi 1 f xi 1
7
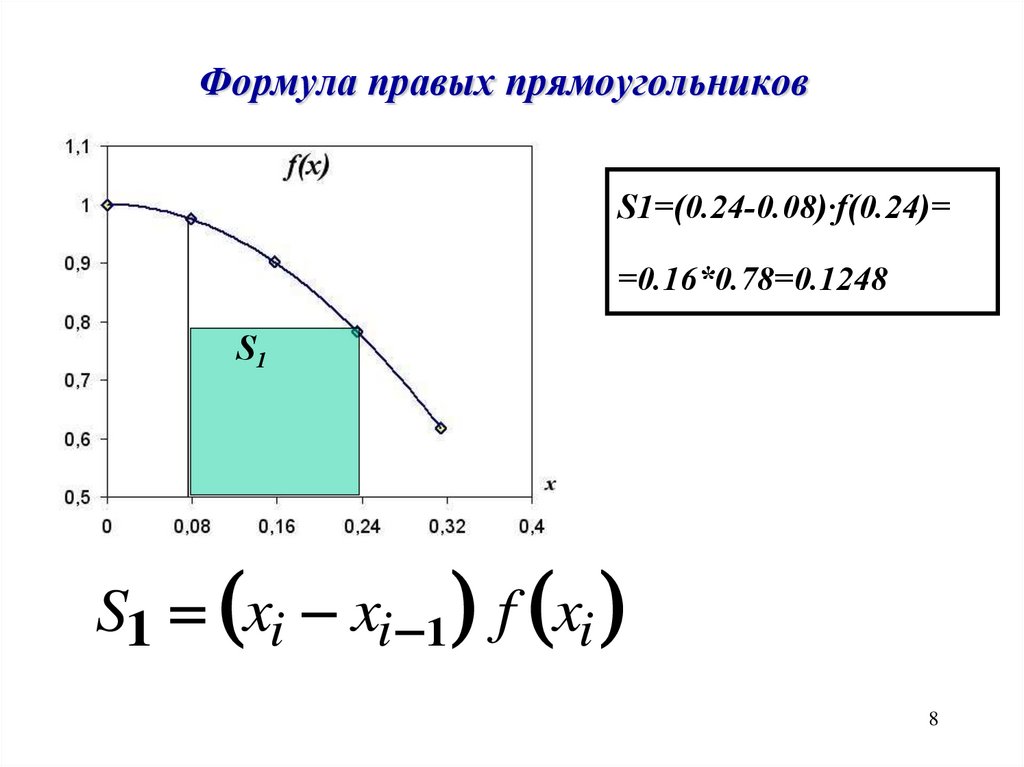
8.
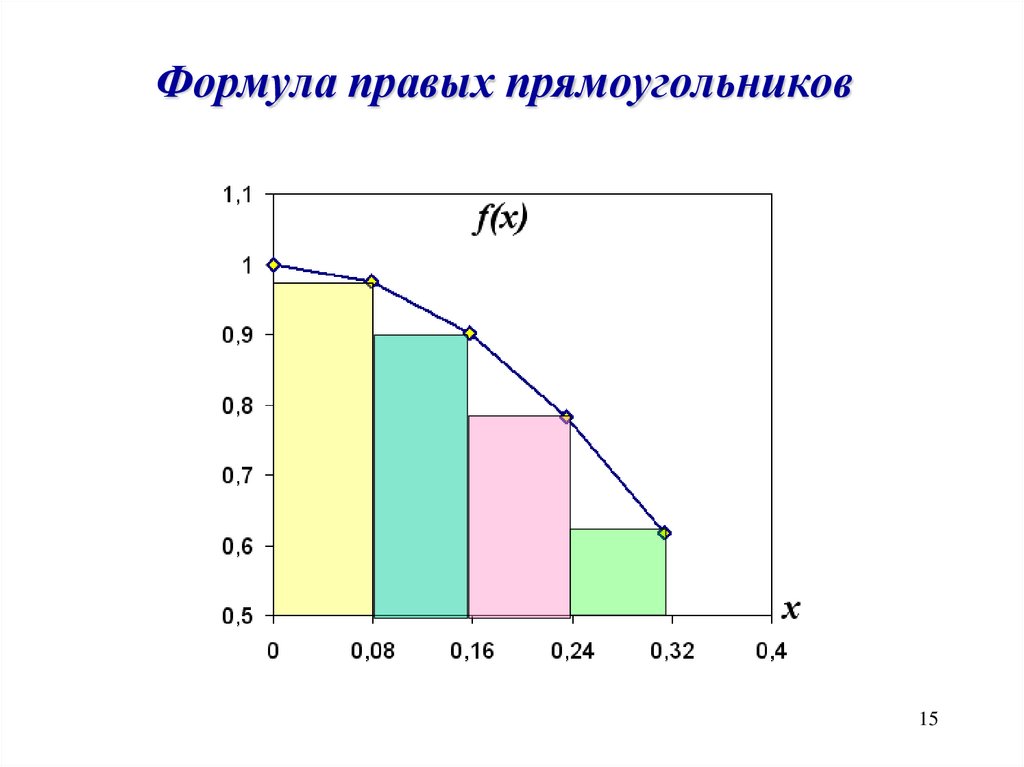
Формула правых прямоугольниковS1=(0.24-0.08)·f(0.24)=
=0.16*0.78=0.1248
S1
S1 xi xi 1 f xi
8
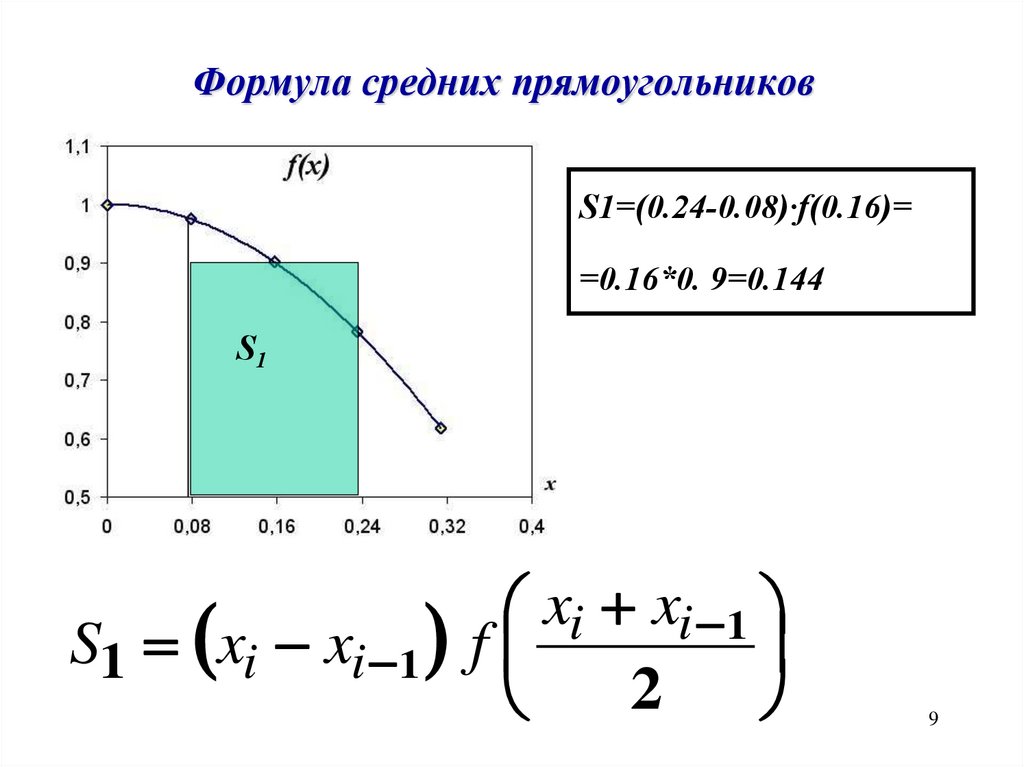
9.
Формула средних прямоугольниковS1=(0.24-0.08)·f(0.16)=
=0.16*0. 9=0.144
S1
xi xi 1
S1 xi xi 1 f
2
9
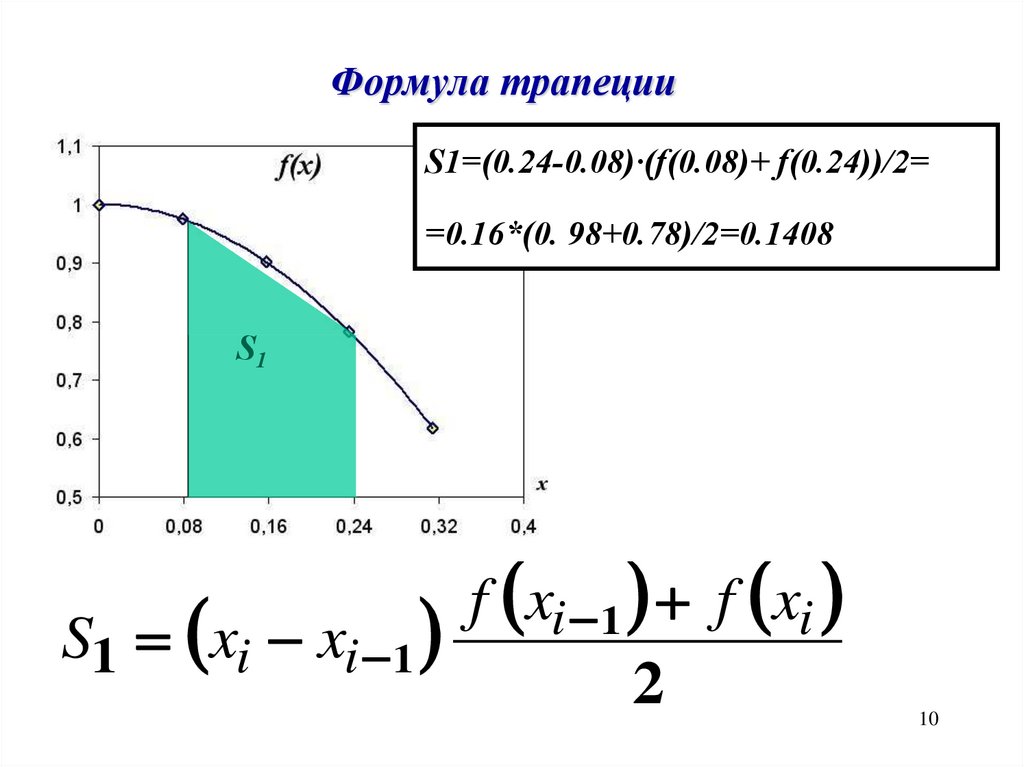
10.
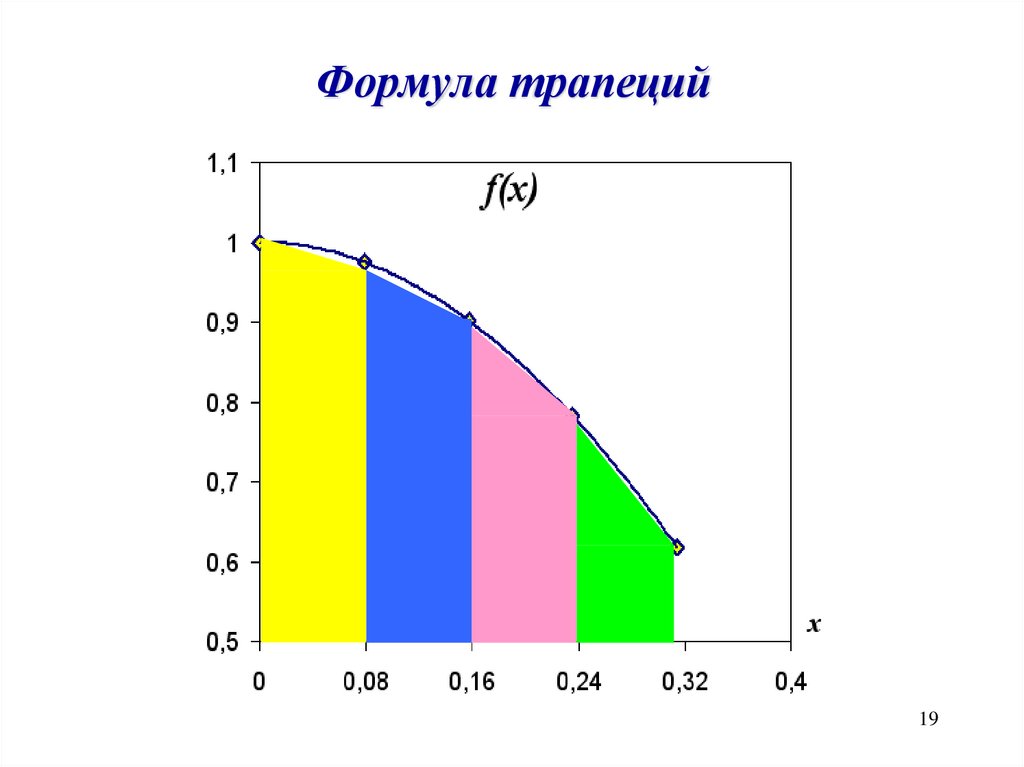
Формула трапецииS1=(0.24-0.08)·(f(0.08)+ f(0.24))/2=
=0.16*(0. 98+0.78)/2=0.1408
S1
f xi 1 f xi
S1 xi xi 1
2
10
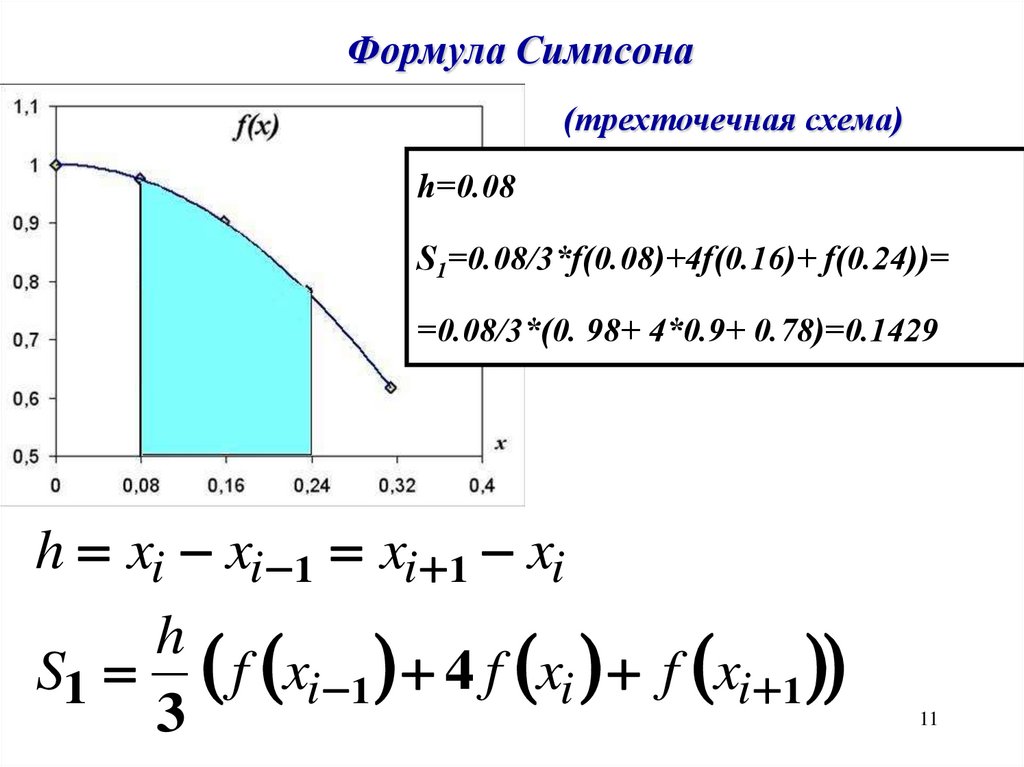
11.
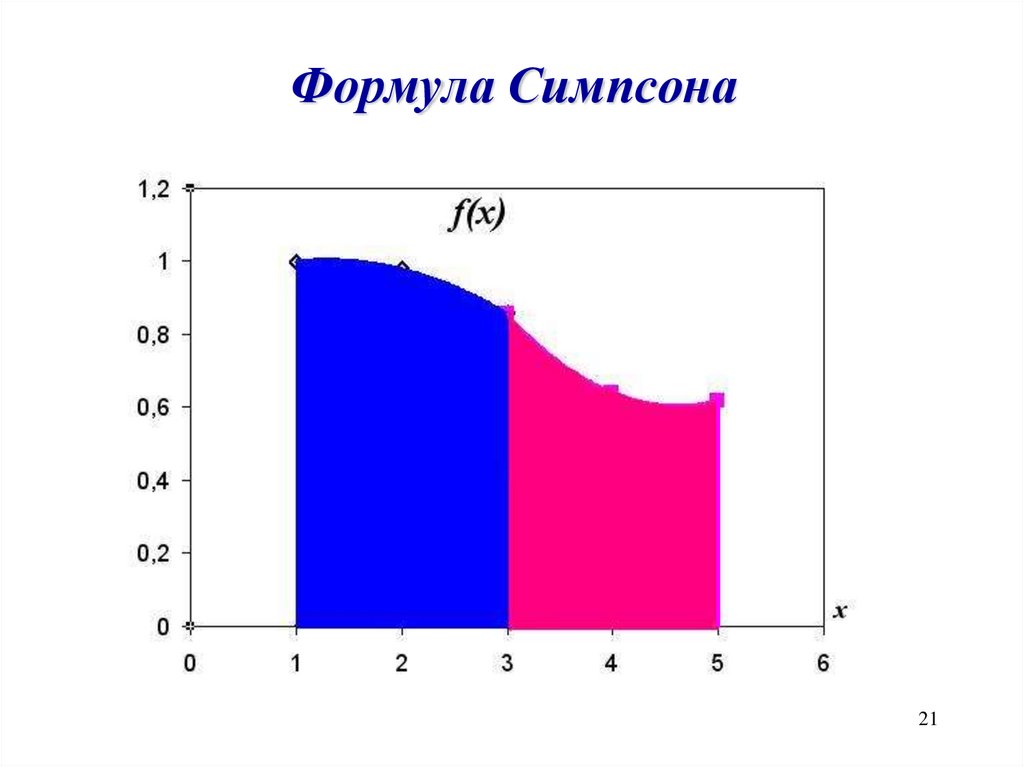
Формула Симпсона(трехточечная схема)
h=0.08
S1=0.08/3*f(0.08)+4f(0.16)+ f(0.24))=
=0.08/3*(0. 98+ 4*0.9+ 0.78)=0.1429
h xi xi 1 xi 1 xi
h
S1 f xi 1 4 f xi f xi 1
3
11
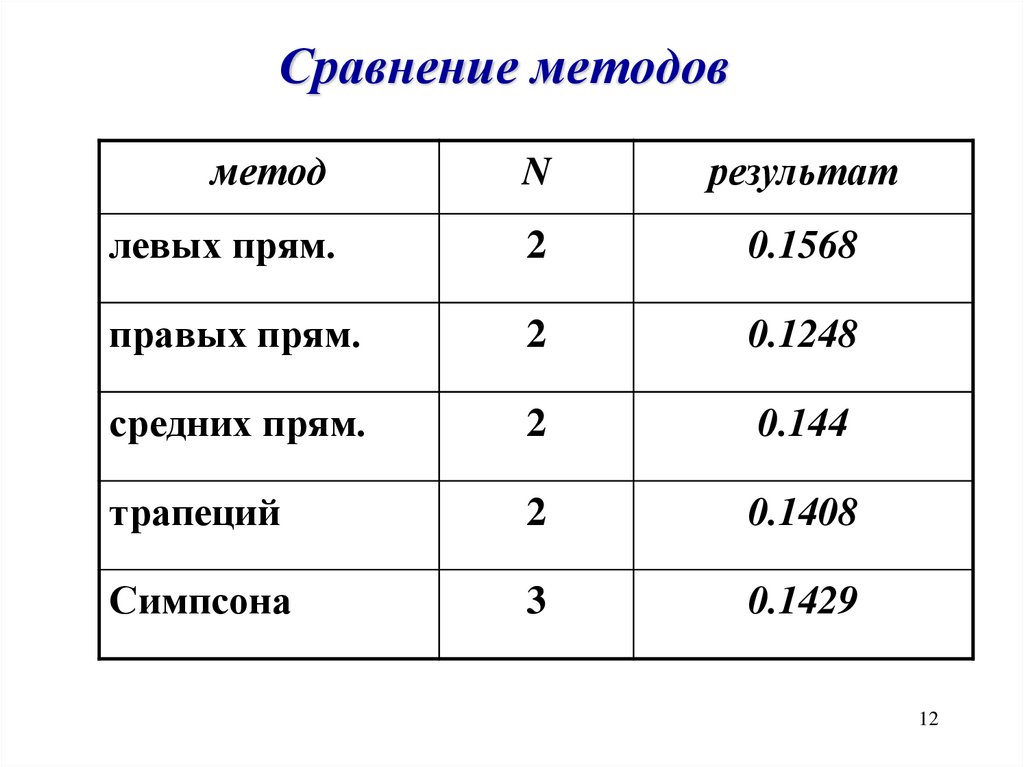
12.
Сравнение методовметод
N
результат
левых прям.
2
0.1568
правых прям.
2
0.1248
средних прям.
2
0.144
трапеций
2
0.1408
Симпсона
3
0.1429
12
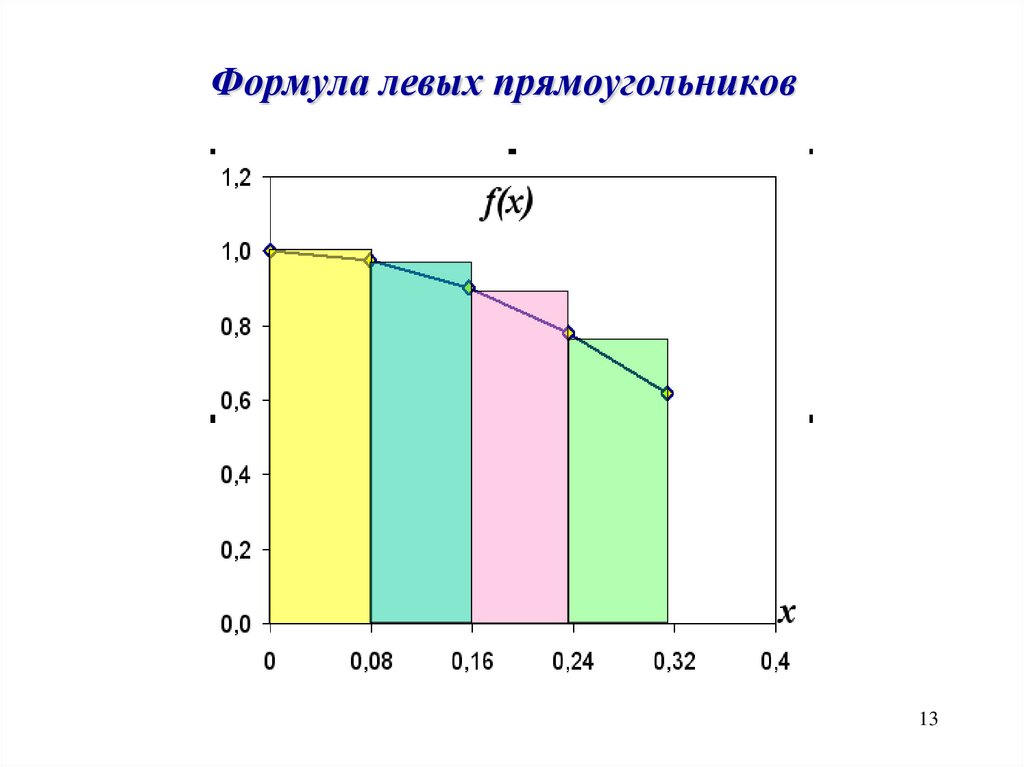
13.
Формула левых прямоугольников13
14.
Метод левых прямоугольниковb
n 1
a
i 0
f
(
x
)
dx
h
f
(
x
)
i
n – количество отрезков
14
15.
Формула правых прямоугольников15
16.
Метод правых прямоугольниковb
n
a
i 1
f
(
x
)
dx
h
f
(
x
)
i
16
17.
Формула средних прямоугольников17
18.
Метод средних прямоугольниковb
n 1
h
f
(
x
)
dx
h
f
(
x
)
i
2
i 0
a
n – количество отрезков
18
19.
Формула трапеций19
20.
Метод трапецийb
1
1
f ( x ) dx h ( 2 f0 f1 f2 ... fn 1 2 fn )
a
20
21.
Формула Симпсона21
22.
Метод Симпсонаb
h
f ( x ) dx ( f0 f n 2 ( f 2 f4 f6 ... f n 2 )
3
a
4 ( f1 f 3 f5 ... f n 1 ))
22
23.
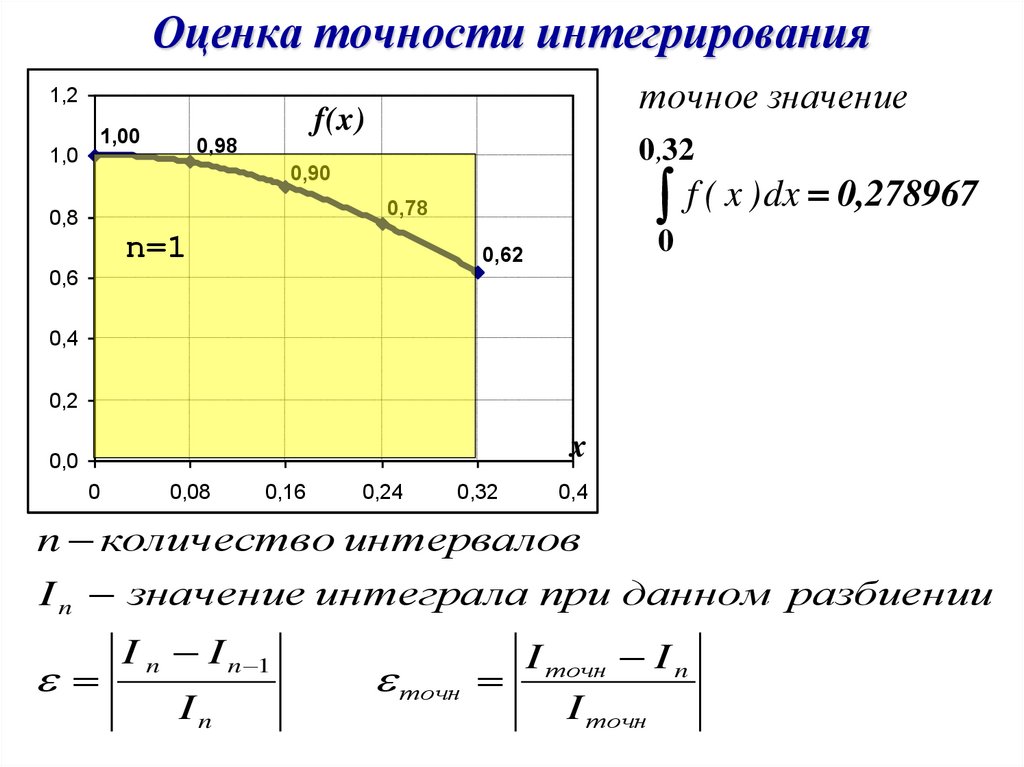
Оценка точности интегрированияточное значение
1,2
1,00
1,0
f(x)
0,98
0 ,32
0,90
f ( x ) dx 0,278967
0,78
0,8
n=1
0
0,62
0,6
0,4
0,2
x
0,0
0
0,08
0,16
0,24
0,32
0,4
n количество интервалов
I n значение интеграла при данном разбиении
I n I n 1
In
I точн I n
точн
I точн
23
24.
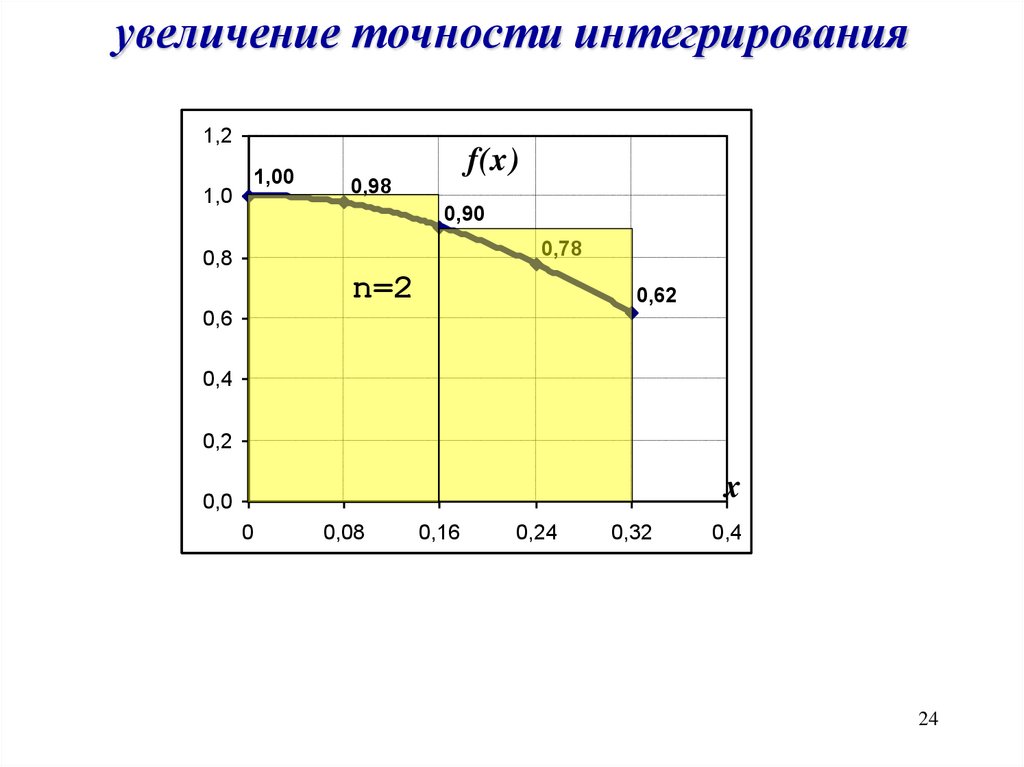
увеличение точности интегрирования1,2
1,0
1,00
f(x)
0,98
0,90
0,78
0,8
n=2
0,62
0,6
0,4
0,2
x
0,0
0
0,08
0,16
0,24
0,32
0,4
24
25.
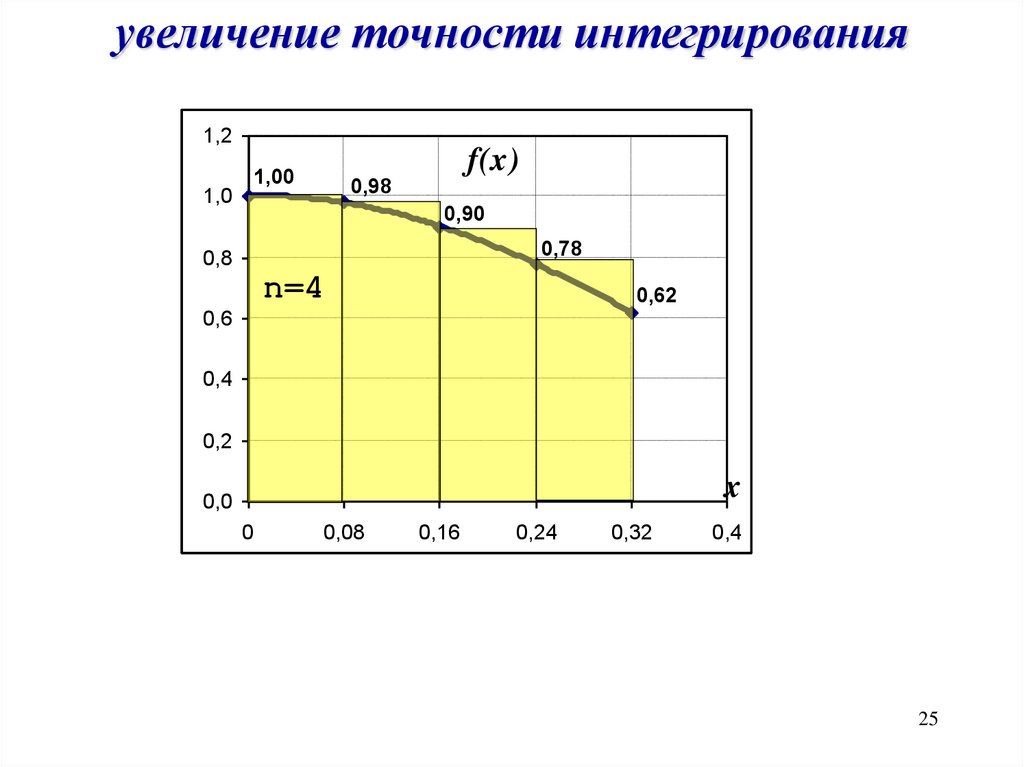
увеличение точности интегрирования1,2
1,0
1,00
f(x)
0,98
0,90
0,78
0,8
n=4
0,62
0,6
0,4
0,2
x
0,0
0
0,08
0,16
0,24
0,32
0,4
25
26.
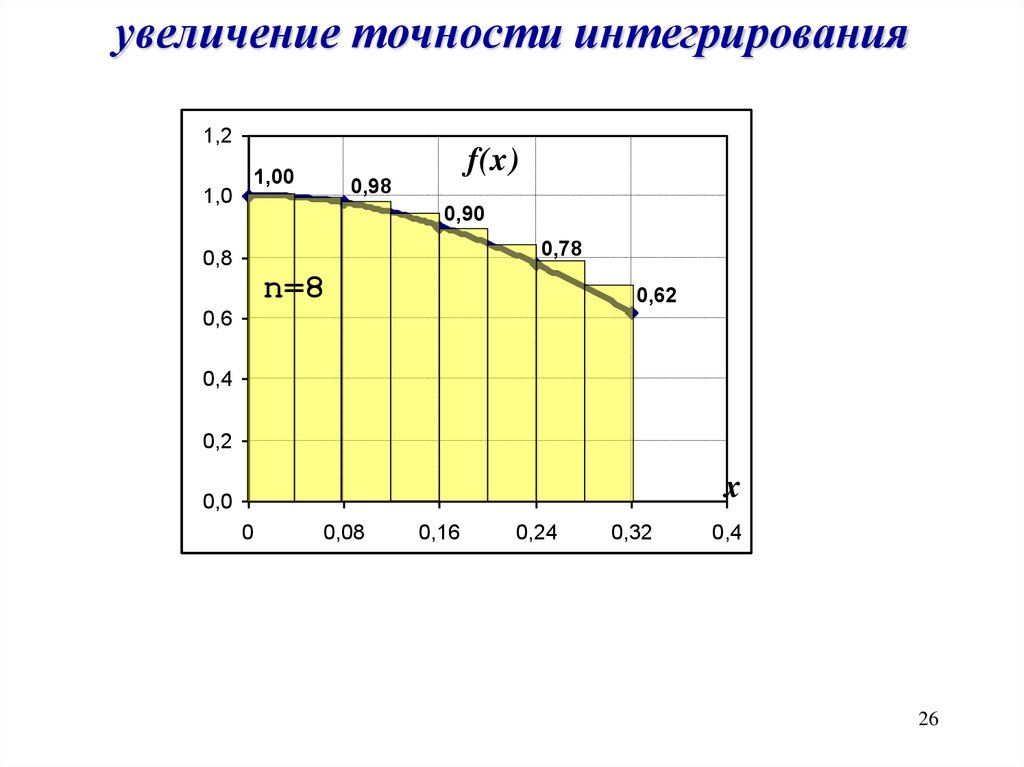
увеличение точности интегрирования1,2
1,0
1,00
f(x)
0,98
0,90
0,78
0,8
n=8
0,62
0,6
0,4
0,2
x
0,0
0
0,08
0,16
0,24
0,32
0,4
26
27.
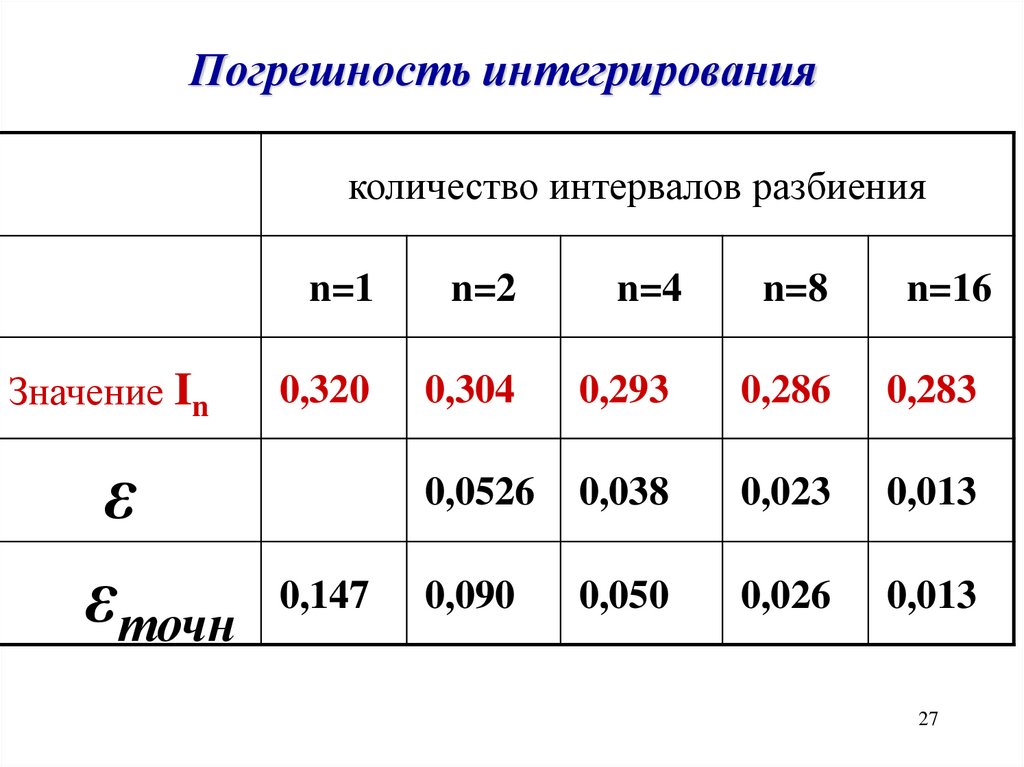
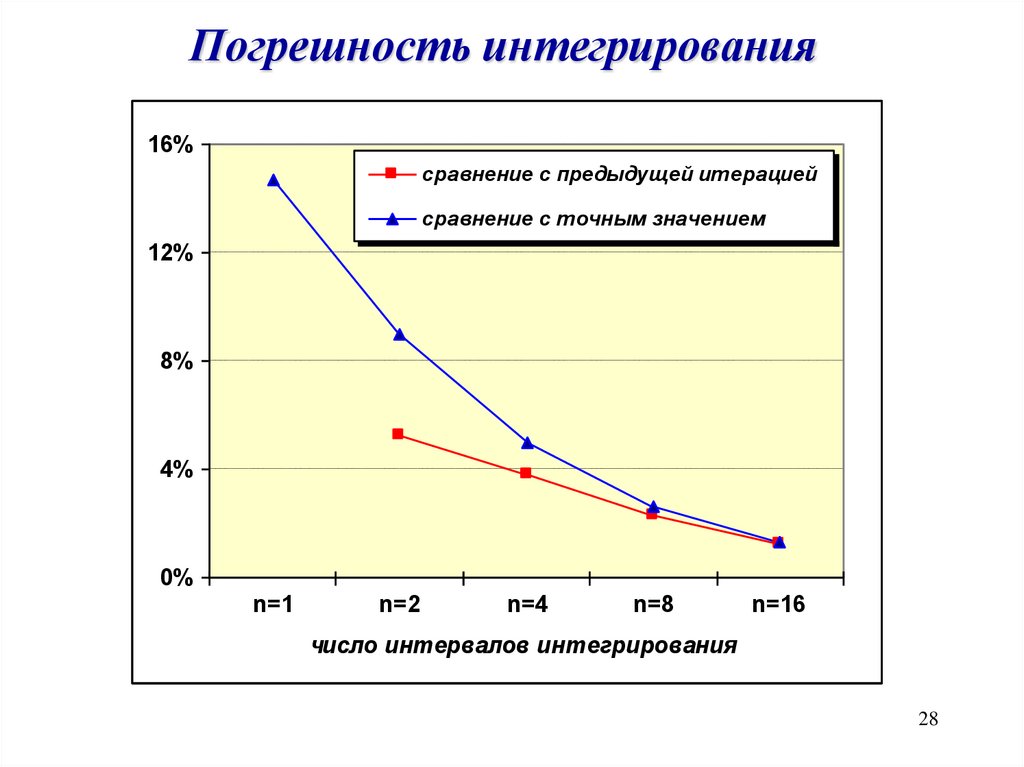
Погрешность интегрированияколичество интервалов разбиения
Значение In
n=1
n=2
n=4
n=8
n=16
0,320
0,304
0,293
0,286
0,283
0,0526
0,038
0,023
0,013
0,090
0,050
0,026
0,013
ε
εточн 0,147
27
28.
Погрешность интегрирования16%
сравнение с предыдущей итерацией
сравнение с точным значением
12%
8%
4%
0%
n=1
n=2
n=4
n=8
n=16
число интервалов интегрирования
28











 Математика
Математика








