Похожие презентации:
Основы теории случайных процессов
Основы теории СЛУЧАЙНЫХ ПРОЦЕССОВ Пространство элементарных событий ( генеральная совокупность)2 Основные понятия теории вероятностей Все сигналы и все помехи являются случайными, то есть непредсказуемыми.
Математическими моделями случайных сигналов и помех служат случайные процессы.
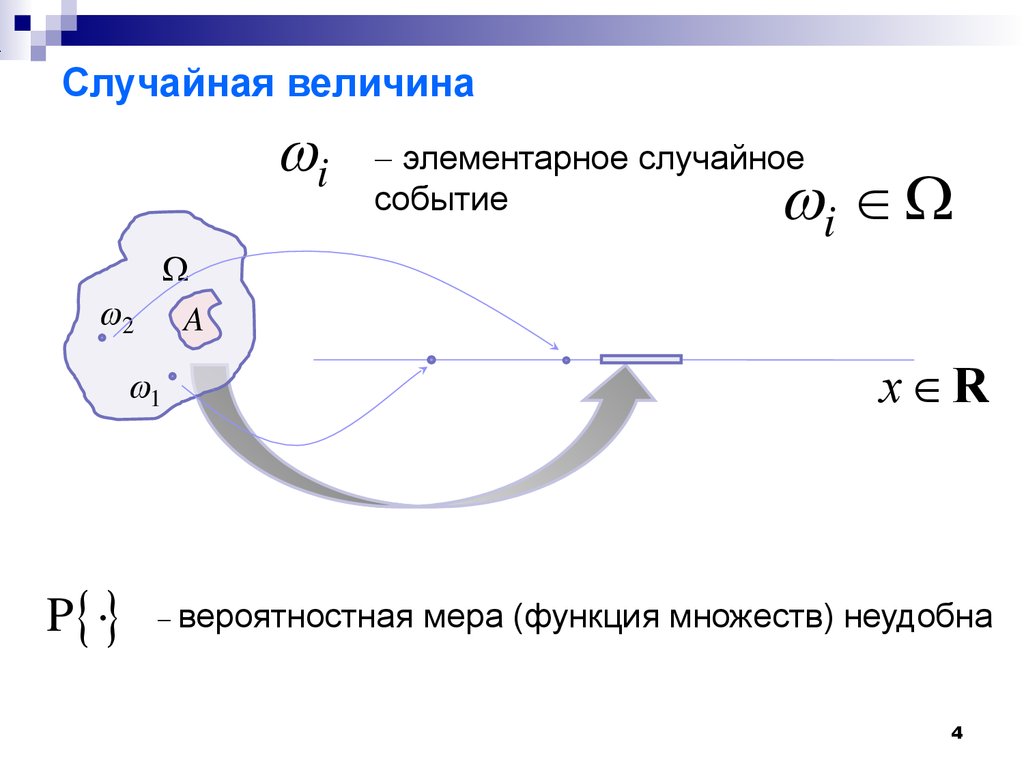
В основе лежит понятие случайного событияA случайное событиеA элементарное событие33 Основные понятия теории вероятностейA случайное событие элементарное случайное событиеA P вероятностная мера (функция множеств) P:20;1 PA вероятность случайного событияA P1 достоверное событиеA44 Случайная величина1Ai элементарное случайное событиеi P вероятностная мера (функция множеств) неудобна2xR55 Случайная величина P вероятностная мера (функция множеств) неудобна ()PFxx функция распределения с.в.()Fxx функция распределения не убывает !166 ()PFxx функция распределения с.в.()Fxx не убывает, но может оставаться постоянной на участках осиx()dFxwxdx()0F ()1F ()()x wxdxFx ()1 wxdx 1 плотность распределения вероятностей77 ()()P FbFaab ()Fxx()dFxwxdx ()()()Pba wxdxFbFaab ab Pab ab188 Примеры ФР и ПРВx()Fxx()wxab1baabx()Fxx()wx ()1,0ax Fxex 1 (),0ax wxaex a равномерное распределение экспоненциальное распределение99 Числовые характеристики с.в.
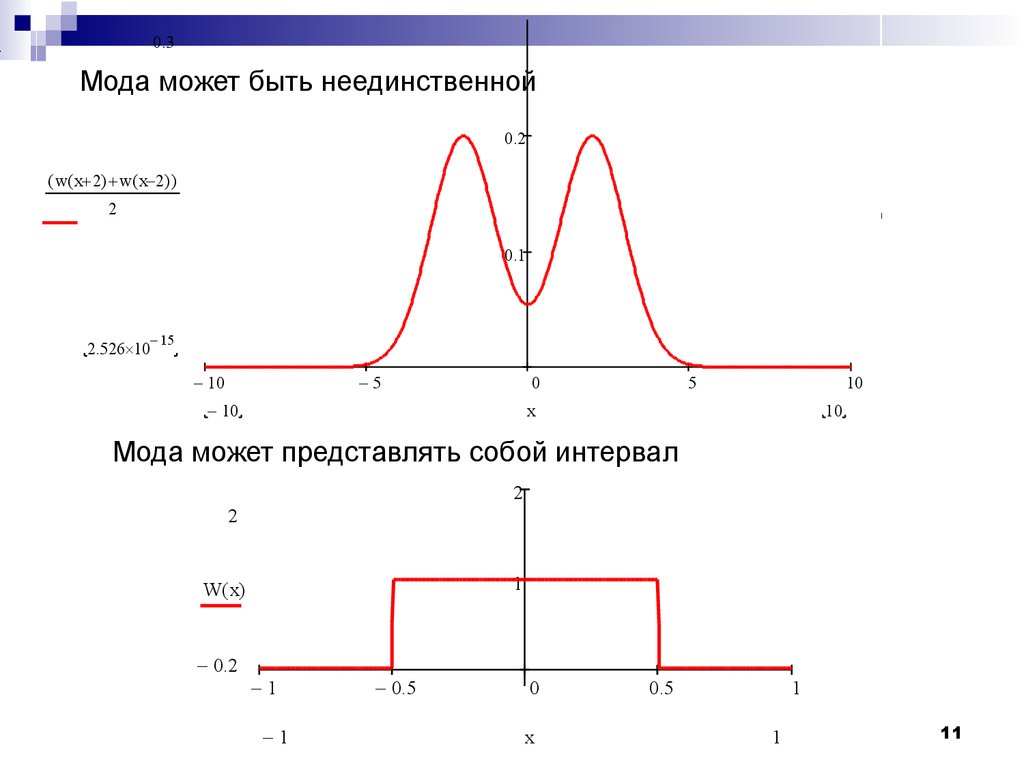
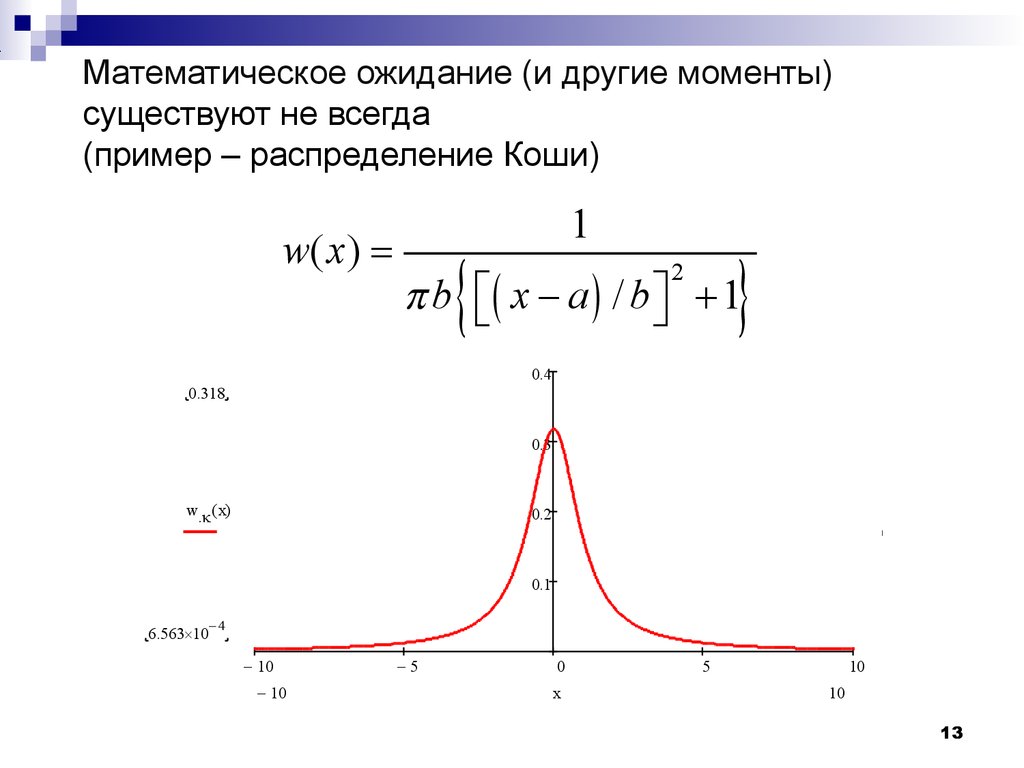
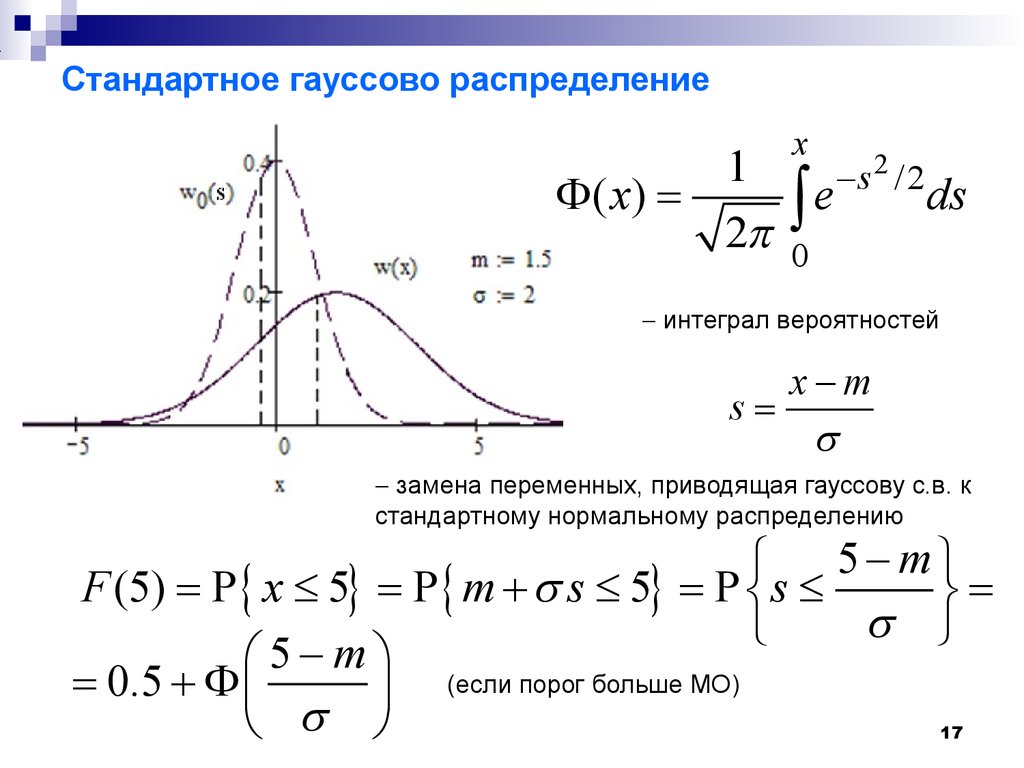
()kkkk mxwxdxxx E начальный моментk- го порядка1() mmxwxdxx начальный момент 1- го порядка, математическое ожидание, «центр распределения»x()wxmem мода медиана10x()wxmem Мода, медиана и математическое ожидание могут совпадать!10 5 05100.10.20.30.40.50wx1()wx4 ()10 x11 Мода может быть неединственной10 5 05100.10.20.3 2.5261015 wx2 ()wx2 ()()210 x1 0.5 00.5120.2 Wx()1 x Мода может представлять собой интервал12 Медиана всегда существует, но может быть не единственна30 20 10 01020300.10.20.30 wx10 ()wx10 ()()222 x1 01230.10.20.30.40.5 0.4290wrx()31 x13 Математическое ожидание (и другие моменты) существуют не всегда (пример – распределение Коши) 21()/1wx bxab 10 5 05100.10.20.30.4 0.318 6.563104 w.x()10 x14 центральный моментk- го порядка ()()k Mxmwxdx 2 ()() DMxmwxdx центральный момент2- го порядка (дисперсия)D()kxm ()kxmE 22 ()() xmxm E среднеквадратическое отклонение (СКО)15 2222 ()()()() DMxmwxdxxmxm E центральный момент2- го порядка (дисперсия)D среднеквадратическое отклонение (СКО) 2222() mxwxdxxx E средний квадрат2 ()() Dxmwxdx 22 (2)() xmxmwxdx 222mmm 2mm 16 Гауссово (нормальное) распределениеD2()21()2xmwxe 2()21()2xmx Fxedx xms стандартное нормальное распределение21()2swse17 Стандартное гауссово распределение50.5m интеграл вероятностейxms 5 (5)P5P5Pm Fxmss замена переменных, приводящая гауссову с.в.
к стандартному нормальному распределению2/201()2xs xeds (если порог больше МО)18 Стандартное гауссово распределение10.5m 1 (1)P1P1Pm Fxmss (если порог меньше МО)19 Иногда используется функция ошибок202 erf()=xt xedt12 ()1erf2xFx 1 ()erf2x 424M20 Числовые характеристики с.в.
Иногда используются дополнительные числовые характеристики, грубо описывающие форму ПРВ Коэффициент эксцесса4243M Коэффициент асимметрии313M (К.
Пирсон) (Р.
Фишер)23113M (К.
Пирсон)21 Системы случайных величин совместная функция распределения (,)P, Fxyxy совместная ПРВ2(,)Fxywxyxy (,)(,)yx Fxywxydxdy 22 Свойства ФР (,)0F (,)1F не убывает по каждому аргументу Свойства ПРВ (,)0wxy (,)1 wxydxdy 23 Совместная (двумерная) функция распределения (,)P, Fxyxy (,)0F (,)1F не убывает по каждому аргументу24 Совместная (двумерная) плотность распределения вероятностей (,)0wxy (,)1 wxydxdy 252(,)Fxywxyxy (,)(,)yx Fxywxydxdy 26 Числовые характеристики системы 2 случайных величин Начальные смешанные моменты(,)kn mxywxydxdy ()()(,)kn knxy Mxmymwxydxdy Центральные смешанные моменты2711(,)xy mxywxydxdyk 11 ()()(,) xyxy MxmymwxydxdyR ковариационный момент корреляционный момент28 Пример .
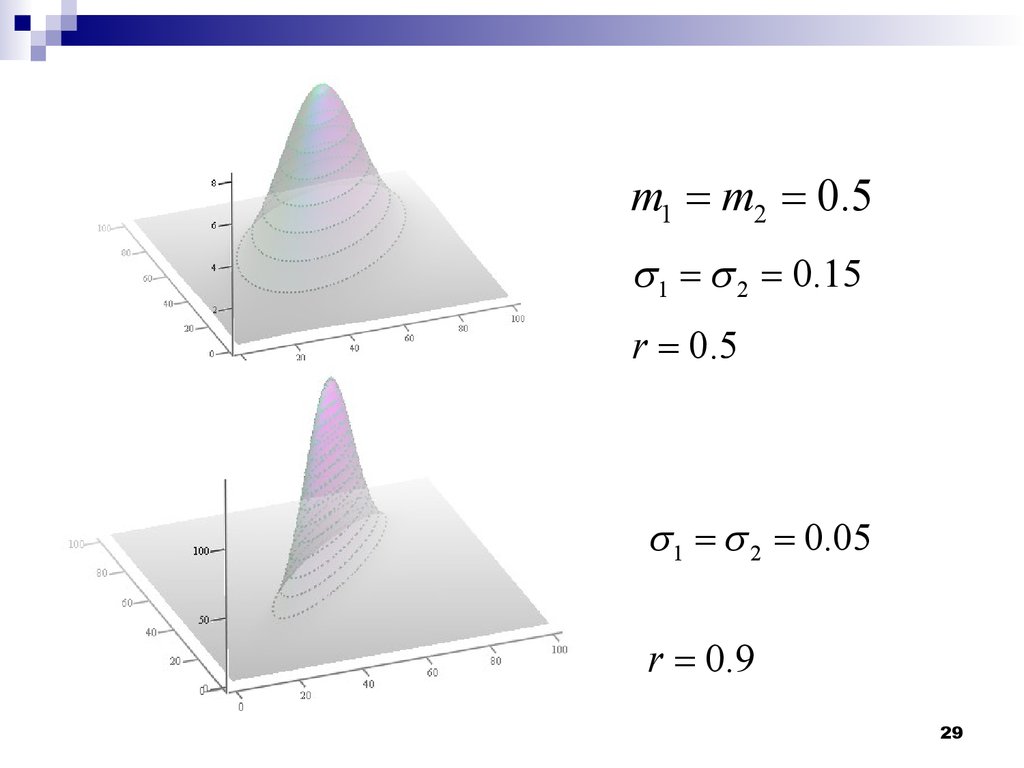
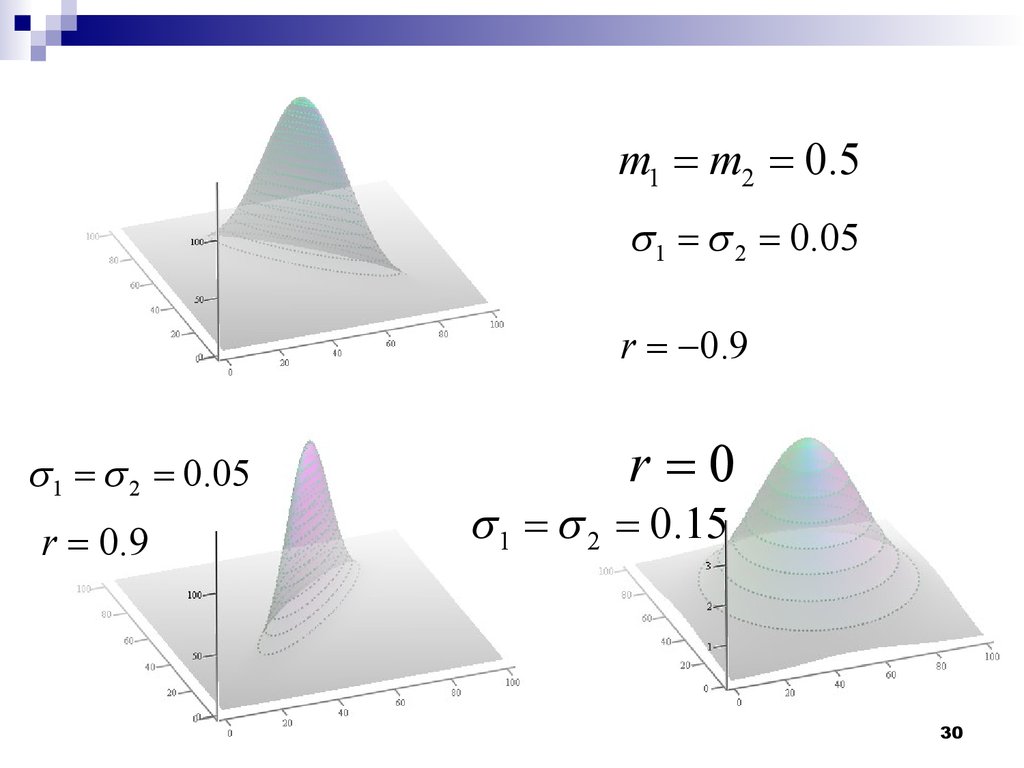
Пара гауссовских случайных величин22 1111222222212 ()()()()12 2(1)122121(,)21 xmxmxmxmr wxxer 12 1122 1212 ()()xxR xmxmr коэффициент корреляции22122212 ()()221211(,)22 xmxm wxxee При нулевом коэффициенте корреляции Некоррелированные гауссовские с.в.
– независимы!12 ()() wxwx290.9r120.5mm 0.5r12 0.05 12 0.15 300.9r12 0.05 120.5mm 0.9r 12 0.05 0r12 0.15
Математическими моделями случайных сигналов и помех служат случайные процессы.
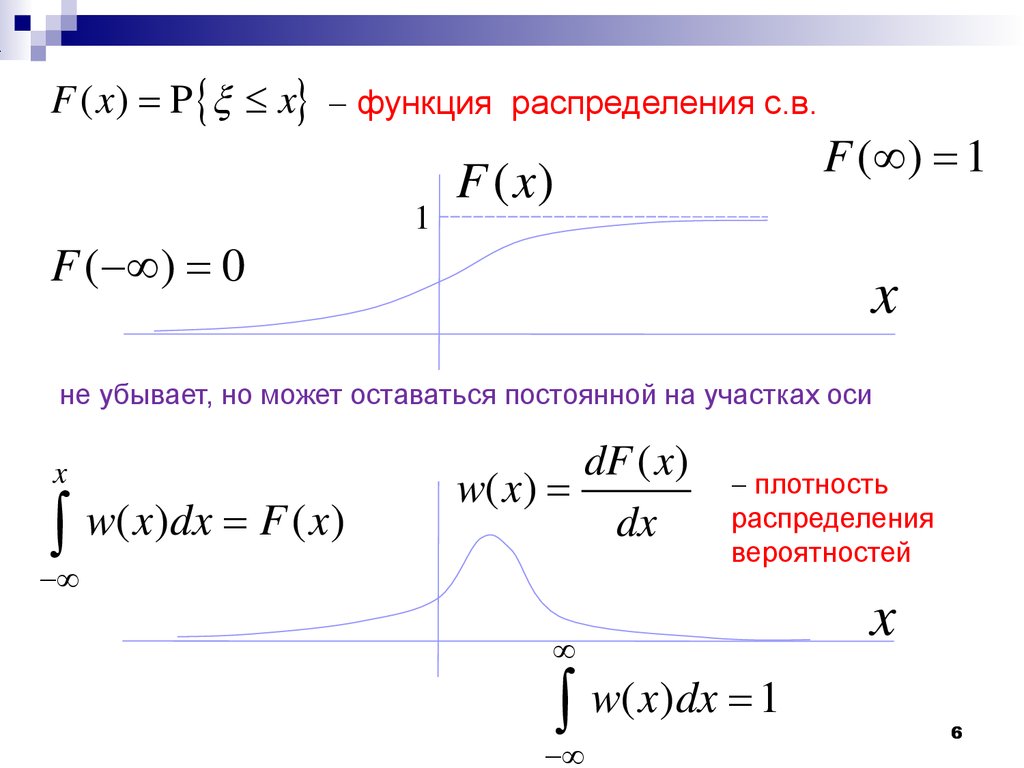
В основе лежит понятие случайного событияA случайное событиеA элементарное событие33 Основные понятия теории вероятностейA случайное событие элементарное случайное событиеA P вероятностная мера (функция множеств) P:20;1 PA вероятность случайного событияA P1 достоверное событиеA44 Случайная величина1Ai элементарное случайное событиеi P вероятностная мера (функция множеств) неудобна2xR55 Случайная величина P вероятностная мера (функция множеств) неудобна ()PFxx функция распределения с.в.()Fxx функция распределения не убывает !166 ()PFxx функция распределения с.в.()Fxx не убывает, но может оставаться постоянной на участках осиx()dFxwxdx()0F ()1F ()()x wxdxFx ()1 wxdx 1 плотность распределения вероятностей77 ()()P FbFaab ()Fxx()dFxwxdx ()()()Pba wxdxFbFaab ab Pab ab188 Примеры ФР и ПРВx()Fxx()wxab1baabx()Fxx()wx ()1,0ax Fxex 1 (),0ax wxaex a равномерное распределение экспоненциальное распределение99 Числовые характеристики с.в.
()kkkk mxwxdxxx E начальный моментk- го порядка1() mmxwxdxx начальный момент 1- го порядка, математическое ожидание, «центр распределения»x()wxmem мода медиана10x()wxmem Мода, медиана и математическое ожидание могут совпадать!10 5 05100.10.20.30.40.50wx1()wx4 ()10 x11 Мода может быть неединственной10 5 05100.10.20.3 2.5261015 wx2 ()wx2 ()()210 x1 0.5 00.5120.2 Wx()1 x Мода может представлять собой интервал12 Медиана всегда существует, но может быть не единственна30 20 10 01020300.10.20.30 wx10 ()wx10 ()()222 x1 01230.10.20.30.40.5 0.4290wrx()31 x13 Математическое ожидание (и другие моменты) существуют не всегда (пример – распределение Коши) 21()/1wx bxab 10 5 05100.10.20.30.4 0.318 6.563104 w.x()10 x14 центральный моментk- го порядка ()()k Mxmwxdx 2 ()() DMxmwxdx центральный момент2- го порядка (дисперсия)D()kxm ()kxmE 22 ()() xmxm E среднеквадратическое отклонение (СКО)15 2222 ()()()() DMxmwxdxxmxm E центральный момент2- го порядка (дисперсия)D среднеквадратическое отклонение (СКО) 2222() mxwxdxxx E средний квадрат2 ()() Dxmwxdx 22 (2)() xmxmwxdx 222mmm 2mm 16 Гауссово (нормальное) распределениеD2()21()2xmwxe 2()21()2xmx Fxedx xms стандартное нормальное распределение21()2swse17 Стандартное гауссово распределение50.5m интеграл вероятностейxms 5 (5)P5P5Pm Fxmss замена переменных, приводящая гауссову с.в.
к стандартному нормальному распределению2/201()2xs xeds (если порог больше МО)18 Стандартное гауссово распределение10.5m 1 (1)P1P1Pm Fxmss (если порог меньше МО)19 Иногда используется функция ошибок202 erf()=xt xedt12 ()1erf2xFx 1 ()erf2x 424M20 Числовые характеристики с.в.
Иногда используются дополнительные числовые характеристики, грубо описывающие форму ПРВ Коэффициент эксцесса4243M Коэффициент асимметрии313M (К.
Пирсон) (Р.
Фишер)23113M (К.
Пирсон)21 Системы случайных величин совместная функция распределения (,)P, Fxyxy совместная ПРВ2(,)Fxywxyxy (,)(,)yx Fxywxydxdy 22 Свойства ФР (,)0F (,)1F не убывает по каждому аргументу Свойства ПРВ (,)0wxy (,)1 wxydxdy 23 Совместная (двумерная) функция распределения (,)P, Fxyxy (,)0F (,)1F не убывает по каждому аргументу24 Совместная (двумерная) плотность распределения вероятностей (,)0wxy (,)1 wxydxdy 252(,)Fxywxyxy (,)(,)yx Fxywxydxdy 26 Числовые характеристики системы 2 случайных величин Начальные смешанные моменты(,)kn mxywxydxdy ()()(,)kn knxy Mxmymwxydxdy Центральные смешанные моменты2711(,)xy mxywxydxdyk 11 ()()(,) xyxy MxmymwxydxdyR ковариационный момент корреляционный момент28 Пример .
Пара гауссовских случайных величин22 1111222222212 ()()()()12 2(1)122121(,)21 xmxmxmxmr wxxer 12 1122 1212 ()()xxR xmxmr коэффициент корреляции22122212 ()()221211(,)22 xmxm wxxee При нулевом коэффициенте корреляции Некоррелированные гауссовские с.в.
– независимы!12 ()() wxwx290.9r120.5mm 0.5r12 0.05 12 0.15 300.9r12 0.05 120.5mm 0.9r 12 0.05 0r12 0.15























 Математика
Математика Физика
Физика