Похожие презентации:
Колебания. Периодическая величина: функция f(t)
1.
Колебания2.
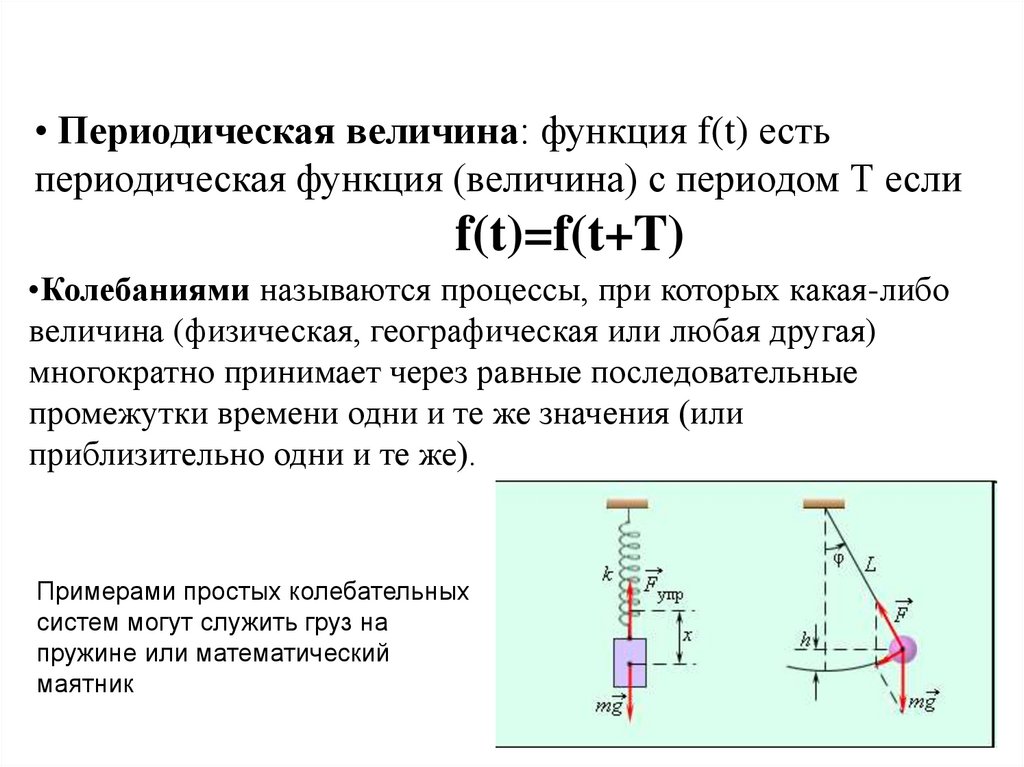
• Периодическая величина: функция f(t) естьпериодическая функция (величина) с периодом Т если
f(t)=f(t+T)
•Колебаниями называются процессы, при которых какая-либо
величина (физическая, географическая или любая другая)
многократно принимает через равные последовательные
промежутки времени одни и те же значения (или
приблизительно одни и те же).
Примерами простых колебательных
систем могут служить груз на
пружине или математический
маятник
3. Свободные, собственные и вынужденные колебания
• Если система каким-либо образом выведена из равновесия изатем предоставлена самой себе (источник устранен), то в ней
происходят колебания, которые называются свободными.
Например, маятник или боксерская груша, выведенная из
положения равновесия однократным ударом.
• Если свободные колебания происходят без потерь энергии, то
они называются собственными, то есть, это- частный случай
свободных колебаний
• Если система колеблется под воздействием периодически
изменяющейся внешней силы, то такие колебания называются
вынужденными. Например, мост под воздействием периодически
повторяющейся внешней силы (проход строевым шагом колонны
солдат).
4. Гармонические колебания
Во многих случаях разнообразные периодическиепроцессы могут быть представлены как суперпозиция
гармонических колебаний. Гармоническими называются
колебания с постоянной амплитудой А, происходящие по
закону синуса или косинуса, то есть когда изменение
физической величины x(t) выражается формулой:
x t Asin t 0 или x(t ) Acos( t 0 )
— круговая или циклическая частота колебаний.
2
2
T
5. Квазиупругие силы
• Силы любого происхождения,пропорциональные величине отклонения
системы от положения равновесия и
направленные к положению равновесия
называются квазиупругими силами. Колебания
под действием квазиупругих сил будут
гармоническими.
• Т.е принципиальное отличие квазиупругих (F=kх) от постоянных (не зависящих от
расстояния и направления перемещения) сил в
том, что воздействие постоянной силы
приводит лишь к смещению положения
равновесия, ничего не меняя в характере самого
движения.
6. Амплитуда, фаза, начальная фаза
Если период равен 1 с, то частота равна 1Гц• Фазой колебаний называется величина
t 0
0— начальная фаза колебаний, то есть фаза при t = 0.
Фаза характеризует отклонение величины х от нулевого
значения в данный момент времени и определяется с
точность до произвольного слагаемого кратного 2
• Амплитуда – максимальное отклонение от положения
равновесия
7. Период и частота колебаний
• Период колебаний T, - время, за которое фазаувеличивается 2 , то есть, значения колеблющейся
величины начинают повторяться.
• Частота v - число колебаний в единицу времени (за 1
1
секунду),
T
•Круговая (циклическая) частота ω - число
колебаний за 2 секунд,
2
T
8. Гармонический осциллятор
• Тело массы m, колеблющееся горизонтально под действием силыупругости пружины F=-kx (k — коэффициент упругости, x —
смещение тела относительно положения равновесия, знак “минус”
означает, что упругая сила направлена противоположно
направлению смещения x) согласно 2-му закону Ньютона запишем:
ma kx или m x kx
Обозначим:
k
k
2
x x 0
0 0
m
m
k
m
x x 0 уравнение гармонического осциллятора
2
0
Решением является:
x A cos( 0t 0 ) или
x A sin( 0t 0 )
• Частота 0 называется собственной частотой данного
гармонического осциллятора.
9.
Скорость и ускорение в гармоническом колебательном движенииточки определяются соответствующими производными по времени:
x A sin( 0t 0 )
v x x ωAcos ωt 0 ωAsin ωt 0
2
2
2
2
a x x ω Asin ωt 0 ω x ω Asin ωt 0
- Скорость изменяется по
гармоническому закону, но ее
амплитуда больше амплитуды х в
раз и опережает х на /2
-Ускорение изменяется по
гармоническому закону, но его
амплитуда больше в 2 раз и
опережает х на
-(т.е. в противофазе с х)
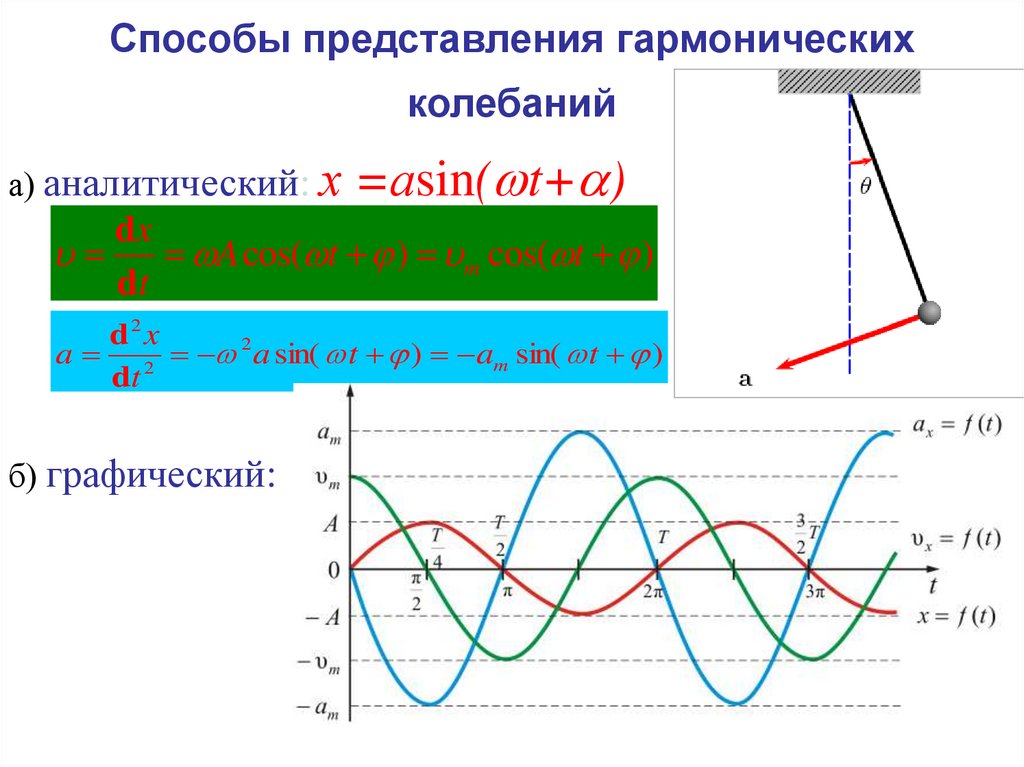
10.
Способы представления гармоническихколебаний
а) аналитический: х =аsin( t+ )
dx
A cos( t ) m cos( t )
dt
d2 x
a 2 2 a sin( t ) am sin( t )
dt
б) графический:
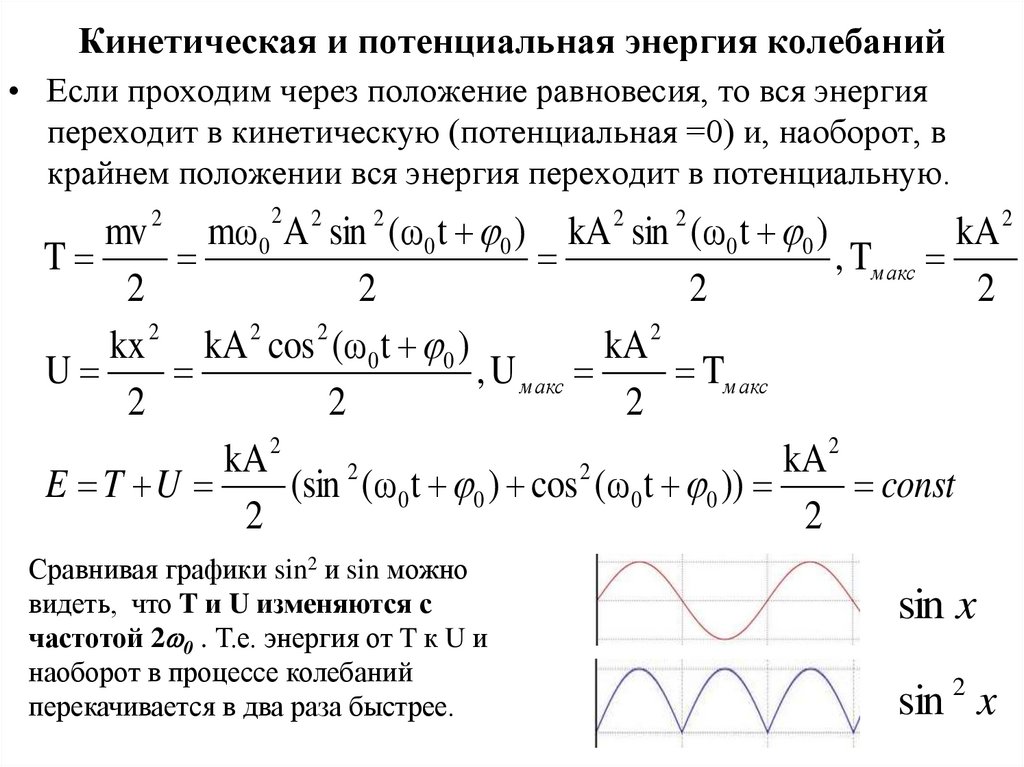
11. Кинетическая и потенциальная энергия колебаний
• Если проходим через положение равновесия, то вся энергияпереходит в кинетическую (потенциальная =0) и, наоборот, в
крайнем положении вся энергия переходит в потенциальную.
mv mω0 A sin (ω0 t 0 ) kA sin (ω0 t 0 )
kA
T
, Tмакс
2
2
2
2
kx 2 kA 2 cos 2 (ω0 t 0 )
kA 2
U
, U макс
Tмакс
2
2
2
2
kA 2
kA
E T U
(sin 2 (ω0 t 0 ) cos 2 (ω0 t 0 ))
const
2
2
2
2
2
2
Сравнивая графики sin2 и sin можно
видеть, что T и U изменяются с
частотой 2 0 . Т.е. энергия от T к U и
наоборот в процессе колебаний
перекачивается в два раза быстрее.
2
2
sin x
2
sin x
2
12. Физический маятник
Fв
0
α
R
c
P
Физическим маятником называется твердое тело,
которое может колебаться вокруг горизонтальной оси
(возможно только при условии, что центр масс тела не
лежит на этой оси). Т.е. нужен ненулевой момент сил.
Движение такого маятника можно описать основным
уравнением динамики для вращательного движения
тела:
I Nвн е ш
x
где I .– момент инерции маятника относительно горизонтальной оси
вращения через точку О. Внешних сил здесь две: сила F упругого
происхождения (изгибает ось), действующая на маятник со стороны оси
в точке 0 и сила тяжести P , приложенная в центре масс. Величина и
направление силы F нам неизвестны, но это неважно, так как она
проходит через ось вращения и поэтому ее момент равен нулю (плечо
равно нулю).
13.
Физический маятникd
d
Iz
I z 2 M z l С , mg lС mg sin
dt
dt
2
Канонический вид уравнения:
d 2
mglС
2
0 sin 0 0
2
dt
Iz
от неподвижной точки (крепления маятника) до центра
lС расстояние
масс тела
В условиях малых колебаний колебания физического маятника можно
рассматривать как линейные колебания:
1; sin
d 2
mglС
2
0 0 0
2
dt
Iz
13
14. Физический маятник
Момент силы тяжести:N = RP = - Rmgsinα = –Pв
F
в
0
α
R
c
P
x
.
где в = Rsinα - плечо силы тяжести. Знак
«минус» означает, что при α >0, то есть при
отклонении против часовой стрелки момент силы
вызывает вращение по часовой стрелке (в
направлении противоположном первоначальному
отклонению). Т.е момент силы тяжести действует
аналогично квазиупругой силе –kx . Итак,
получаем:
I = –mgRsinα
При малых (при α <<1 в радианной мере) sinα ≈ α и
+ ω2α = 0
,
где
R- расстояние от оси вращения до центра масс
2 =
mgR
I
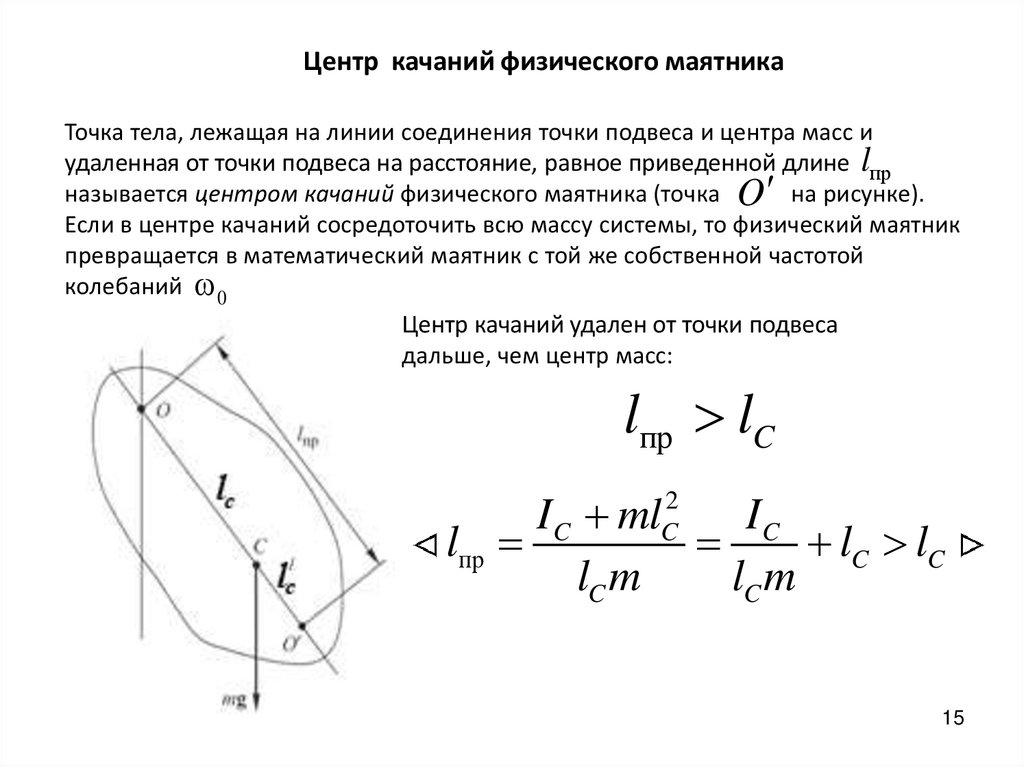
15.
Центр качаний физического маятникаТочка тела, лежащая на линии соединения точки подвеса и центра масс и
удаленная от точки подвеса на расстояние, равное приведенной длине lпр
называется центром качаний физического маятника (точка O на рисунке).
Если в центре качаний сосредоточить всю массу системы, то физический маятник
превращается в математический маятник с той же собственной частотой
колебаний 0
Центр качаний удален от точки подвеса
дальше, чем центр масс:
lпр lC
I C mlC2
IC
lпр
lC lC
lC m
lC m
15
16.
Теорема ГюйгенсаЕсли точку подвеса и центр качаний поменять местами («оборотный маятник»),
частота колебаний маятника не изменится.
Доказательство.
Покажем, что приведенная длина прямого и оборотного маятника одинаковы
IC 2
IC
lпрlC lC lC lпр lC lC lC
m
m
IC
lC
mlC
I C m lC
I z
IC
lпр
lC lC lпр lC lпр
lC m
lC m
mlC
2
g / lпр 0
0 g / lпр
16
17.
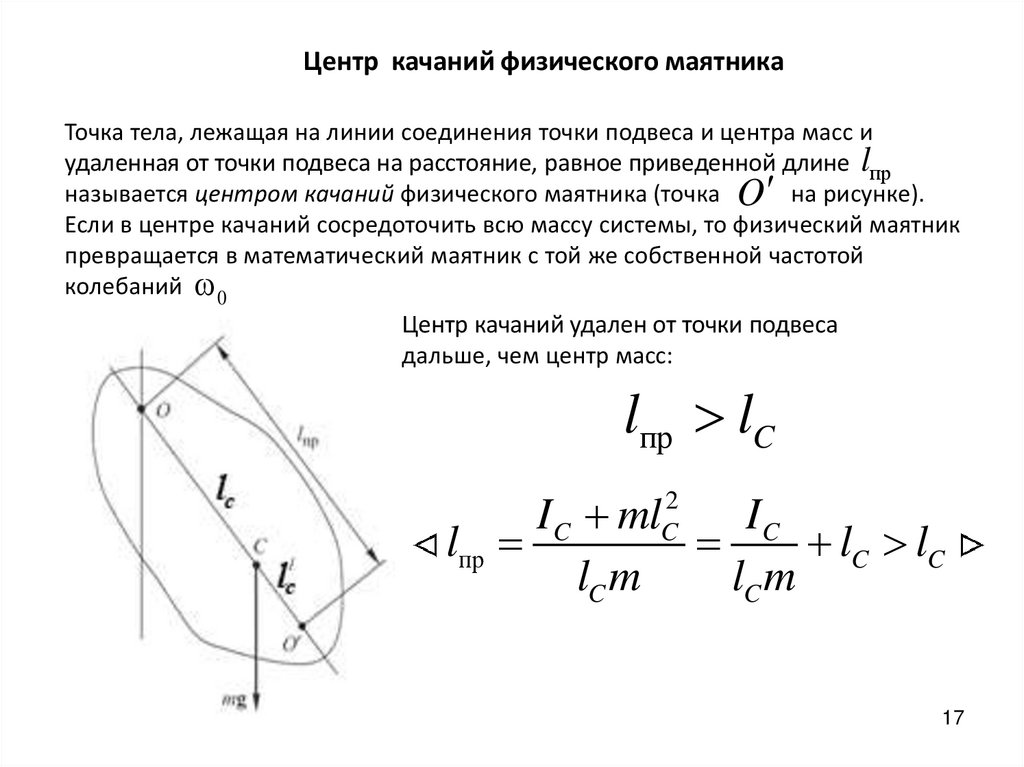
Центр качаний физического маятникаТочка тела, лежащая на линии соединения точки подвеса и центра масс и
удаленная от точки подвеса на расстояние, равное приведенной длине lпр
называется центром качаний физического маятника (точка O на рисунке).
Если в центре качаний сосредоточить всю массу системы, то физический маятник
превращается в математический маятник с той же собственной частотой
колебаний 0
Центр качаний удален от точки подвеса
дальше, чем центр масс:
lпр lC
I C mlC2
IC
lпр
lC lC
lC m
lC m
17
18. Физический маятник
В результате имеем дифференциальное уравнениегармонических колебаний, решением которого как нам
уже известно является функция:
α (t) = Asin(ωt+φ)
mgR
I
где циклическая частота
ω
а период колебаний
I
T 2π
mgR
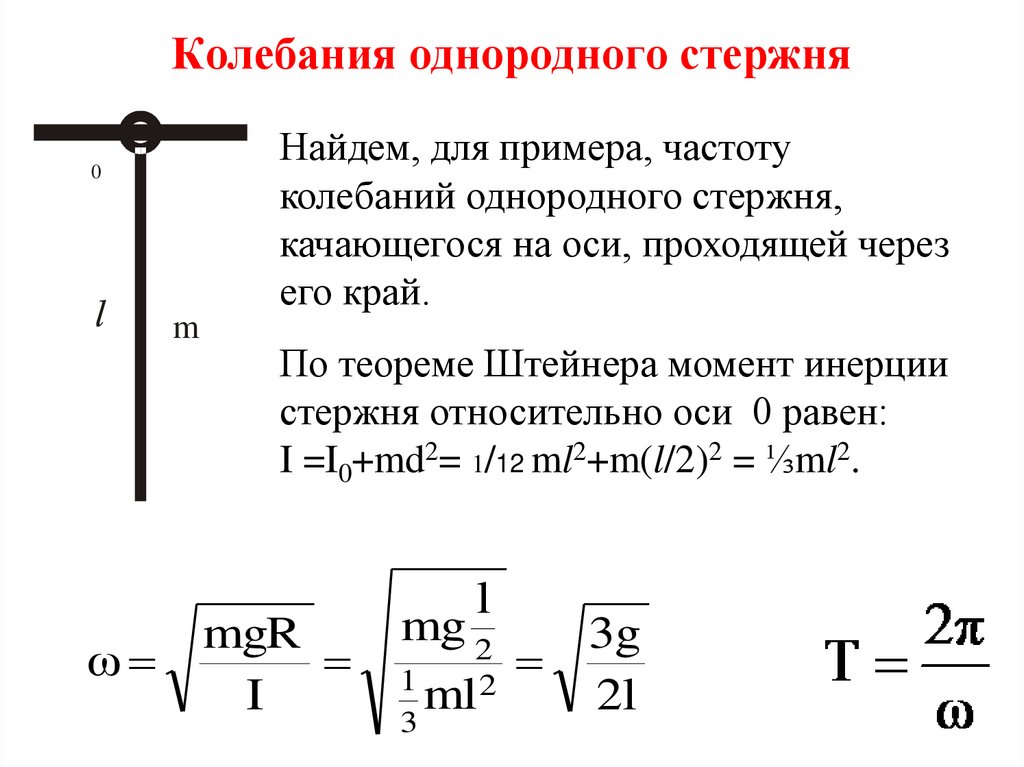
19. Колебания однородного стержня
Найдем, для примера, частотуколебаний однородного стержня,
качающегося на оси, проходящей через
его край.
0
m
ω
По теореме Штейнера момент инерции
стержня относительно оси 0 равен:
I =I0+md2= 1/12 ml2+m(l/2)2 = ⅓ml2.
mgR
I
l
mg 2
3g
1
ml 2
2l
3
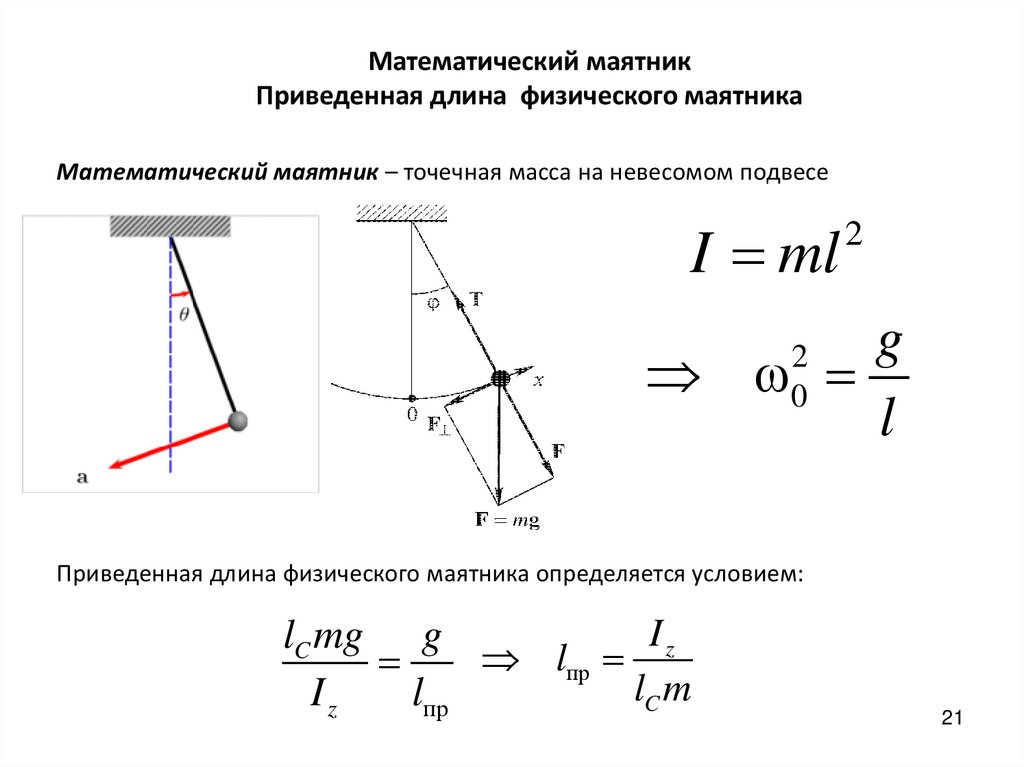
20. Математический маятник
Математическим маятником называется тело,массу которого можно считать сосредоточенной
в одной точке, подвешенное на невесомой,
нерастяжимой нити. Он оказывается частным
случаем физического маятника.
Момент инерции материальной точки I = ml2
m
ω
mgR
I
mgl
g
2
l
ml
2π
l
T
2π
ω
g
Т.е. из- за разного характера распределения массы есть
отличие в частоте колебаний математического маятника и
стержня той же длины и массы.
21.
Математический маятникПриведенная длина физического маятника
Математический маятник – точечная масса на невесомом подвесе
I ml
2
g
l
2
0
Приведенная длина физического маятника определяется условием:
Iz
lC mg g
lпр
lC m
Iz
lпр
21
22.
Математический и физический маятники2π
l
T
2π
ω
g
Приведённая длина — это условная характеристика физического
маятника. Она численно равна длине математического маятника,
период которого равен периоду данного физического маятника.
Приведённая длина вычисляется следующим образом:
где I — момент инерции относительно точки подвеса, m — масса, a
— расстояние от точки подвеса до центра масс.
Период колебаний математического маятника зависит от его
длины и ускорения силы тяжести и не зависит от массы груза.
Измерив период колебаний маятника, можно определить ускорение
свободного падения g в данном месте.
Частота собственных колебаний зависит только от свойств системы
(ω02 = k/m для математического и ω02 = mgR/I для физического маятников),
23. Превращения энергии при колебаниях
Пружинный маятник.В
процессе
колебаний
происходит
превращение
кинетической энергии груза в потенциальную энергию
деформированной пружины и обратно.
Физический маятник .
В
процессе
колебаний
происходит
превращение
кинетической энергии маятника в потенциальную
гравитационную энергии и обратно.
Электромагнитные колебания.
В процессе колебаний происходит превращение энергии
электрического поля в энергию магнитного поля и обратно.
23
24. Затухающие колебания
• Если нельзя пренебрегать сопротивлением среды призаписи 2-го закона Ньютона для движения тела под
действием упругой силы, то его надо дополнить
некоторой функцией, отражающей свойства сил
сопротивления (сил трения).
• Например, если тело все время движется в жидкости с
малыми скоростями, то сила трения пропорциональна
скорости и второй закон Ньютона записывается так:
m x kx k1x
или в стандартном для дифференциальных уравнений
виде :
k
k
x
1
m
x
m
x 0
25. Затухающие колебания
k2
Обозначим:
ω0 (как и ранее) и
m
k1
β
2m
дифференциальное уравнение затухающих колебаний:
x 2βx ω x 0
2
0
Решение уравнений такого типа в математике хорошо
известно и в нашем случае выглядит так:
βt
x(t) A e sin( t ) A(t)sin( t )
0
Заметим, что здесь фигурирует не собственная частота колебаний
ω0 , а частота ω , которая зависит от коэффициента затухания β:
02 2
Частота свободных колебаний зависит как от свойств системы (ω0), так и от
величины потерь энергии (β )
26. Декремент затухания
• Быстроту затухания описывают также с помощью декрементазатухания или с помощью логарифмического декремента
затухания. Декрементом затухания Δ называют отношение двух
последовательных амплитуд:
Δ
A(t)
A(t T)
eβT
• Логарифмическим декрементом затухания δ называют
натуральный логарифм обычного декремента затухания:
δ = lnΔ = βT
• если величина β фиксирована, то величина δ прямо
пропорциональна периоду колебаний. Например, если δ=0.01 то
амплитуда уменьшится в e раз после 100 колебаний. Быстроту
затухания колебаний определяется β= δ/T.
• Добротность системы Q. При больших добротностях δ /Q
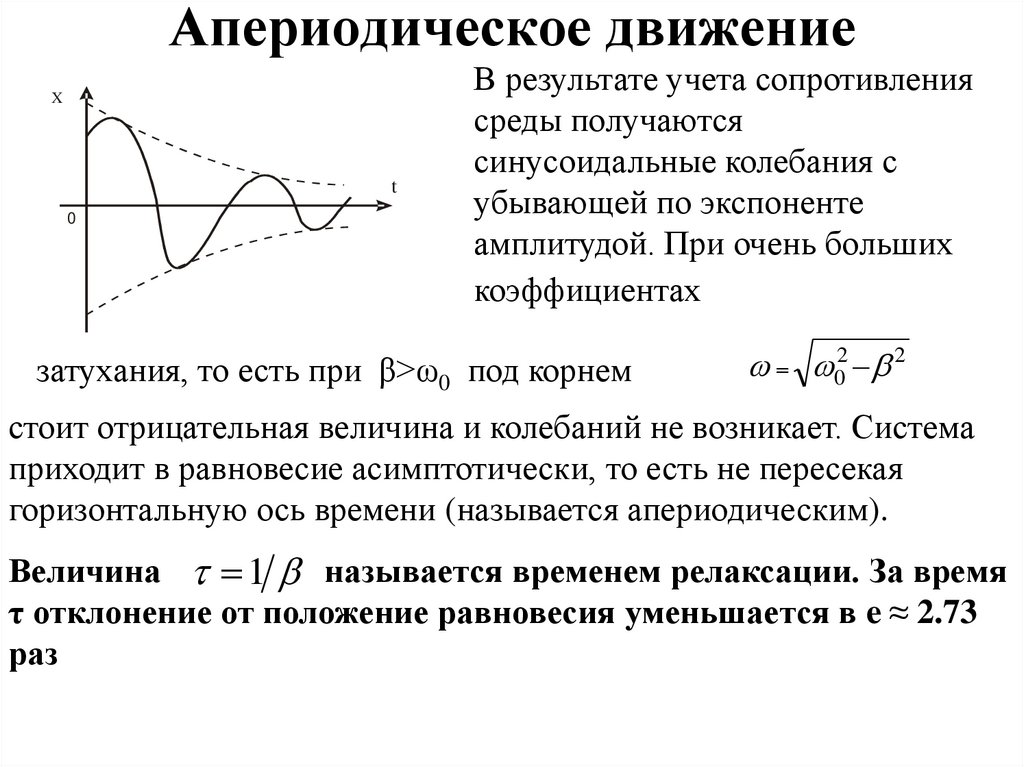
27. Апериодическое движение
Xt
0
В результате учета сопротивления
среды получаются
синусоидальные колебания с
убывающей по экспоненте
амплитудой. При очень больших
коэффициентах
затухания, то есть при β>ω0 под корнем
02 2
стоит отрицательная величина и колебаний не возникает. Система
приходит в равновесие асимптотически, то есть не пересекая
горизонтальную ось времени (называется апериодическим).
Величина 1 называется временем релаксации. За время
τ отклонение от положение равновесия уменьшается в e ≈ 2.73
раз
28.
Добротностьдобротность колебательной системы –
пропорциональна числу колебаний Ne, совершаемых
системой за то время τ , за которое амплитуда колебаний
уменьшается в е раз
Q= π/λ= πNe
Полная энергия колеблющейся системы
E k
m x
x
x
m
2
2
2
2
2
2
0
ω= ω02-δ2
2
m
xm A0 exp( t )
При слабом затухании
колебаний добротность
пропорциональна
Убыль энергии за 1 период
отношению энергии,
dE E E
2 ET энергия за 1 период запасенной в системе в
dt T
T
данный момент к убыли
этой энергии за один
E
2
E
период колебаний. Малое
Q=π/λ
2 ET 2
ET
Q
ET
затухание δ →большая
1
1
E
добротность →
(
)
относительно малые
Q 2
ET
потери энергии.
относительная потеря энергии за период
dE
2 E
dt
29. Вынужденные колебания
• Колебания, происходящие в системе под действиемпериодически изменяющейся силы, называются вынужденными.
• Пусть тело колеблется под действием упругой силы и на него
действует внешняя сила :
Fвнеш (t)= F0sinΩt
учитывая используемые выше уравнения, второй закон Ньютона
запишем в виде:
x 2βx ω x
2
0
Fo
sin t
Подобные уравнения описывают широкийm
спектр процессов вплоть до
описания движения доменных стенок в магнитных материалах, где m
эффективная масса доменной стенки.
30. Вынужденные колебания
• Опыт показывает, что если вынуждающая сила действуетдостаточно долго, то груз колеблется с частотой вынуждающей
силы Ω и с постоянной амплитудой. Поэтому можно
предположить, что раз вынуждающая сила гармоническая, то и
установившиеся колебания также будут гармоническими:
x = Asin(Ωt + φ)
Частота вынужденных колебаний равна частоте
вынуждающей силы
• Надо найти амплитуду А и начальную фазу φ этого колебания.
Для этого можно взять первую и вторую производную x подставить
все в уравнение движения. Если произвести ряд громоздких
преобразований, то можно получить следующие соотношения:
31. Амплитуда и фаза
AF0
m (ω Ω ) 4β Ω
2
0
2
2
2
2
2
tg 2
0 2
Разность фаз колебаний вынуждающей силы и груза φ :
2
arctg 2
02
• Прямой подстановкой можно убедиться, что это
решение удовлетворяет исходному уравнению движения.
• В полученном решении и амплитуда, и фаза зависят от
частоты вынуждающей силы.
32. Резонанс
Есть зависимость амплитуды от частоты и значит при некоторойчастоте возможна максимальная амплитуда. Это будет тогда, когда
знаменатель в выражении движения достигнет минимума. Чтобы
найти минимум, приравняем нулю производную по частоте Ω
знаменателя:
2( )( 2 ) 8 0
2
0
2
2
Это кубическое уравнение имеет, естественно, три корня:
Ω1 = 0
и
2,3 02 2 2
Это есть точки экстремума знаменателя. Решение Ω1 = 0
соответствует максимуму знаменателя. При этом амплитуда
F0
F0
А0
2
mω 0 k
33. Резонансная частота
• Из двух оставшихся решений отрицательное отбрасываем как неимеющее физического смысла, так как частота отрицательной
быть не может. Следовательно, амплитуда будет максимальной при
следующей частоте вынуждающей силы:
рез 02 2 2
• Эта частота называется резонансной, а само явление возрастания
амплитуды вынужденных колебаний при приближении частоты
вынуждающей силы к собственной частоте системы называется
резонансом.
• Отметим, что резонансная частота не совпадает с собственной
частотой колебаний системы ω0, но близка к ней и тем ближе, чем
меньше трение в системе.
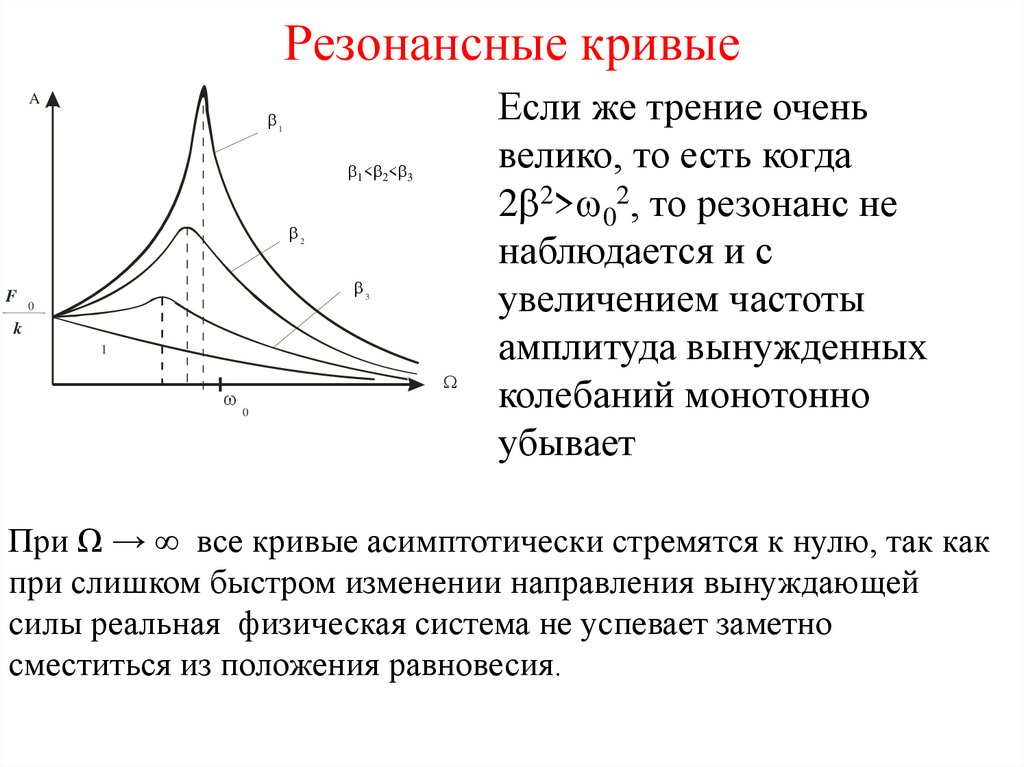
34. Резонансные кривые
A1
1< 2< 3
2
3
F 0
k
1
0
Если же трение очень
велико, то есть когда
2 2> 02, то резонанс не
наблюдается и с
увеличением частоты
амплитуда вынужденных
колебаний монотонно
убывает
При Ω → ∞ все кривые асимптотически стремятся к нулю, так как
при слишком быстром изменении направления вынуждающей
силы реальная физическая система не успевает заметно
сместиться из положения равновесия.
35.
Добротность показывает во сколько разамплитуда в момент резонанса
превышает смещение системы из
положения равновесия под действием
вынужденной силы той же величины, что и
амплитуда вынуждающей силы.
(Это справедливо лишь при небольших
затуханиях).
36.
Характеристики затухания колебаний.постоянная затухания колебаний;
1/ время жизни колебаний – время, в течении которого
амплитуда уменьшается в e раз
В присутствие силы вязкого трения колебания
продолжаются бесконечно долго. Сухое трение делает это
время конечным
x(t ))
d ln
T T / коэффициент
натуральному
x(t T )
затухания,
равный
логарифму
отношения
максимальных
последовательных
отклонений от состояния равновесия
(«часть жизни, прожитая осциллятором за
один цикл колебаний»)
N / T количество циклов колебаний совершаемых
осциллятором за время жизни
0
Q
2 T0 2d
- добротность осциллятора (quality factor);
характеризует потери энергии за период колебаний
Все безразмерные характеристики используют сравнение с «собственной
единицей времени» осциллятора - его периодом.
36
37.
Динамика изменения скорости затухающих колебанийV x Ae t sin t cos t
Ae
sin t
cos t
2 2
2 2
Ae t 0 cos t Ae t 0 sin t / 2 ;
t
2
2
arctg arctg
2 2
0
В присутствие вязкого трения увеличивается разность фаз между колебаниями
скорости и координаты
37
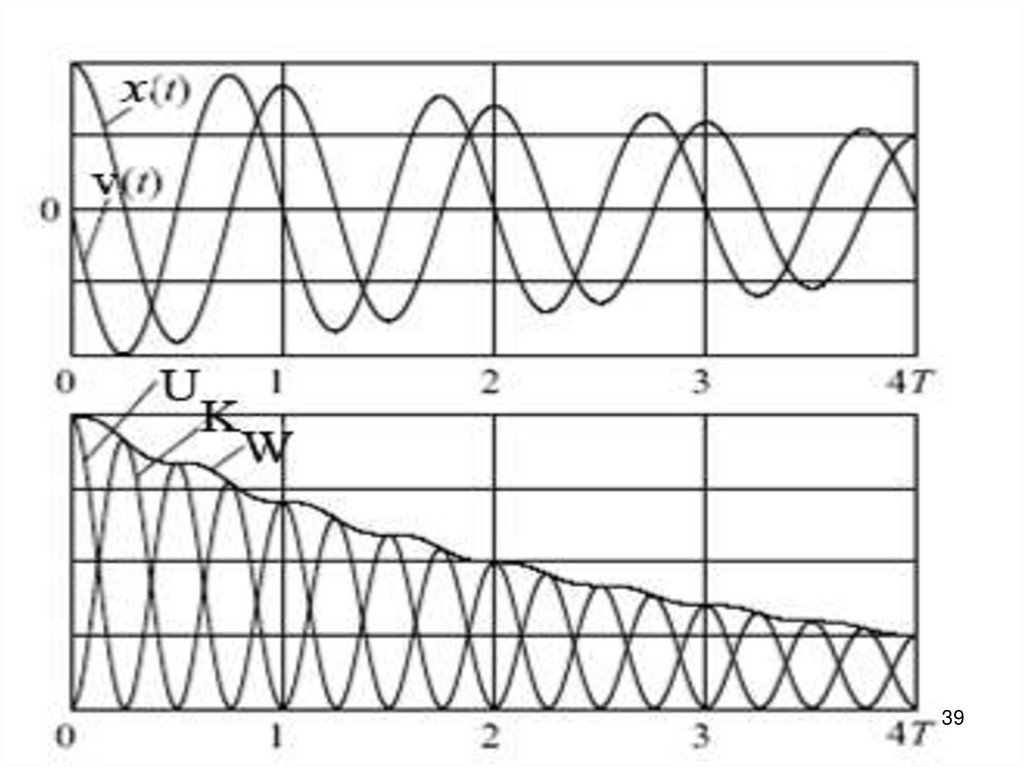
38.
Динамика изменения энергии затухающих колебанийmV 2 kx 2 mV 2 m 02 x 2
W K U
2
2
2
2
1 2 2 t 2
A e m 0 cos 2 ( t ) sin 2 ( t )
2
kA2 2 t 1
1
e 1 cos 2( t ) cos 2( t )
2
2
2
kA2 2 t
e 1 sin sin 2( t )
2
Скорость изменение полной механической энергии затухающего осциллятора
равна мощности диссипативной силы:
dW
dV
2 dx
mV
m 0 x mx( x 02 x) x 2
dt
dt
dt
Рассеяния энергии на периоде колебаний происходит неравномерно: скорость
рассеяния больше в те промежутки времени, когда скорость осциллятора и,
следовательно, его кинетическая энергия, велика, т.е. при нахождении тела вблизи
38
состояния равновесия.
39.
3940.
Рассеянье энергии при слабом тренииПусть коэффициент силы сопротивления достаточно мал, так что за один
период колебаний рассеяние энергии невелико:
1/ T
1
m 02 2 2 t kA2 2 t
W K U W (t )dt
Ae
e
T0
2
2
T
k 2 2 t W
K U A e
4
2
Изменение во времени усредненной энергии определяется уравнением:
d W
2 W
dt
Относительно изменение энергии за период равно
W
1
2 T
W
Q
W
Q
W
40
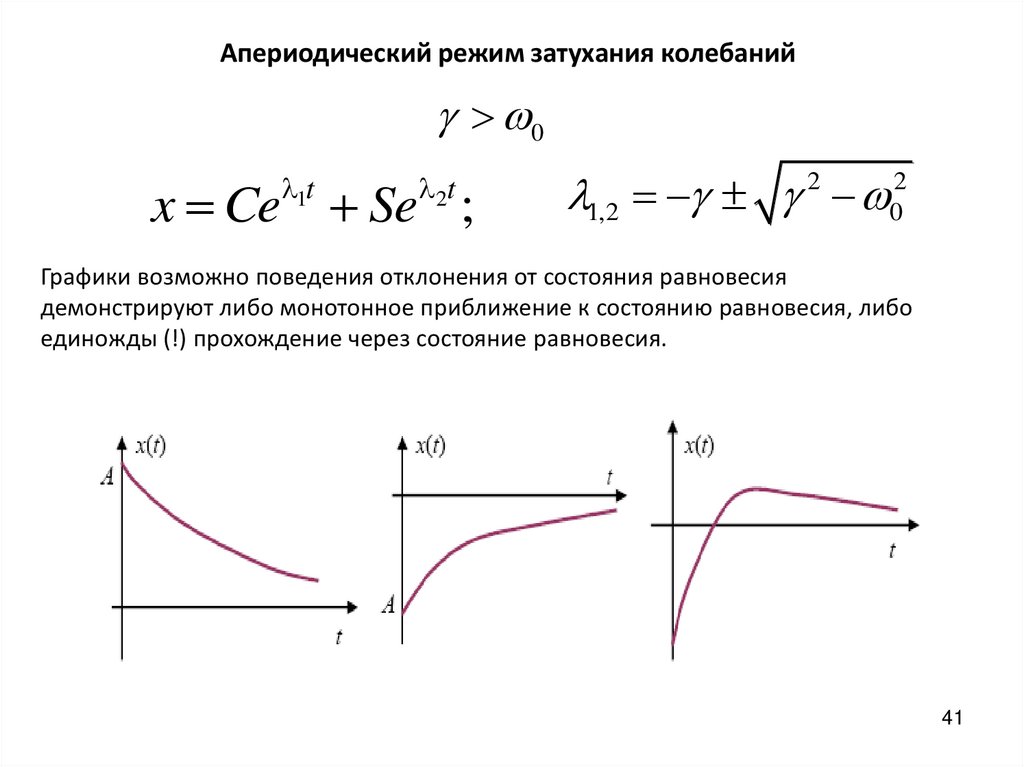
41.
Апериодический режим затухания колебаний0
1t
2t
x Ce Se ;
1,2 2 02
Графики возможно поведения отклонения от состояния равновесия
демонстрируют либо монотонное приближение к состоянию равновесия, либо
единожды (!) прохождение через состояние равновесия.
41
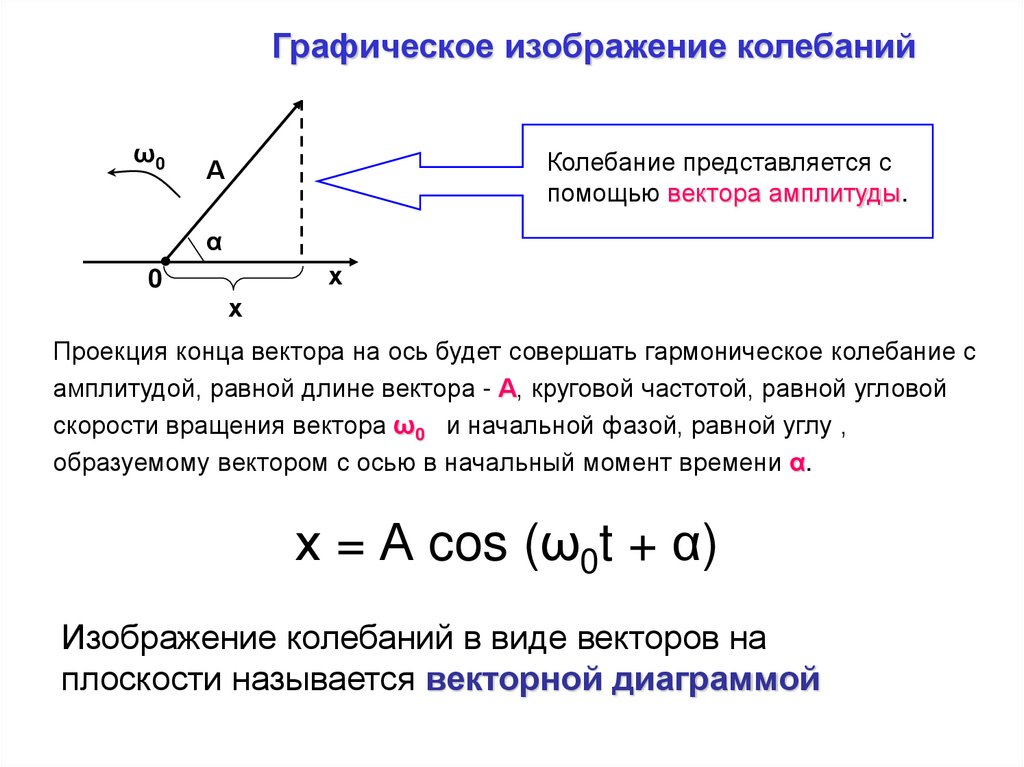
42.
Графическое изображение колебанийω0
Колебание представляется с
помощью вектора амплитуды.
А
α
х
0
х
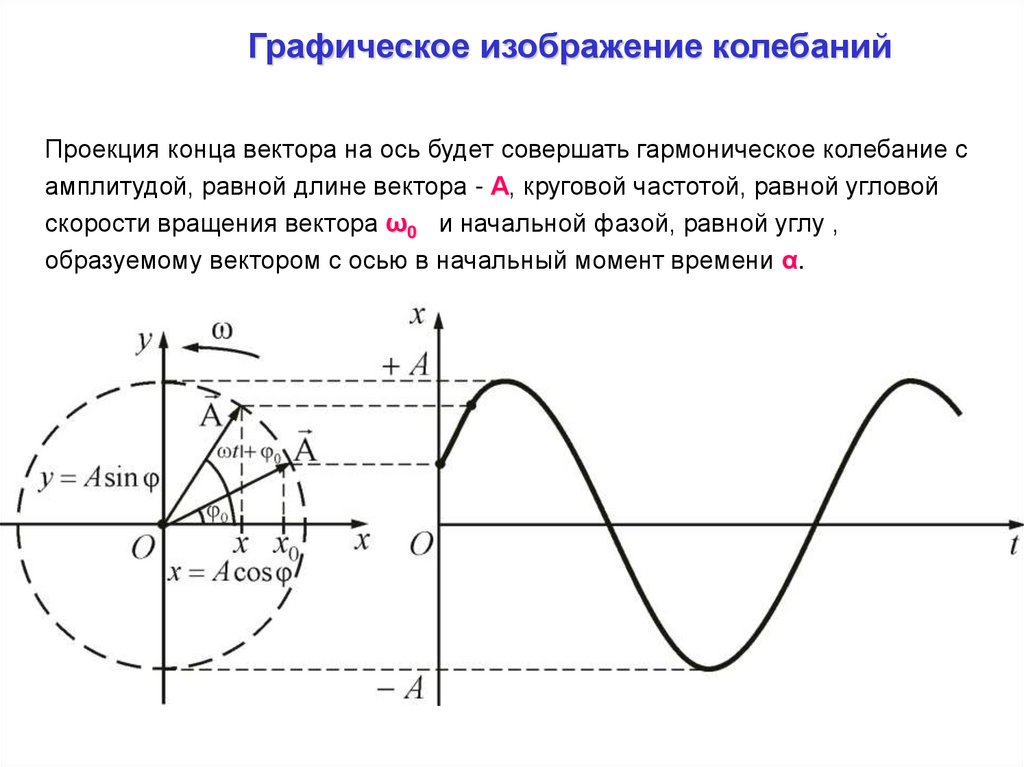
Проекция конца вектора на ось будет совершать гармоническое колебание с
амплитудой, равной длине вектора - А, круговой частотой, равной угловой
скорости вращения вектора ω0 и начальной фазой, равной углу ,
образуемому вектором с осью в начальный момент времени α.
х = А cos (ω0t + α)
Изображение колебаний в виде векторов на
плоскости называется векторной диаграммой
43.
Графическое изображение колебанийПроекция конца вектора на ось будет совершать гармоническое колебание с
амплитудой, равной длине вектора - А, круговой частотой, равной угловой
скорости вращения вектора ω0 и начальной фазой, равной углу ,
образуемому вектором с осью в начальный момент времени α.
44.
Сложение колебанийКолеблющееся тело может участвовать в нескольких колебательных
процессах, тогда необходимо найти результирующее колебание, иными
словами, колебания необходимо сложить. Сложим гармонические
колебания одного направления и одинаковой частоты. Смещение х
колеблющегося тела будет суммой смещений х1 и х2, которые запишутся
в следующим образом:
х1 = А1cos(ω0t+ φ1)
х2 = А2cos(ω0t+ φ2)
Представим оба колебания с помощью векторов A1 и A2. Построим по
правилам сложения векторов результирующий вектор A
45.
Сложение колебанийА1 и А2- амплитуды складываемых
колебаний под углами φ1 и φ2 к оси х
А - вектор амплитуды суммарного
колебания.
х1 = А1cos(ω0t+ φ1)
х2 = А2cos(ω0t+ φ2)
Определим модуль амплитуды А результирующего колебания. В ΔОК1К угол
ОК1К= [π-(φ2-φ1)] (из равенства противоположных углов параллелограмма).
Следовательно 2 (φ2-φ1)+2α=2π
Отсюда α= [π-(φ2-φ1)]
Согласно теореме косинусов
А2=А12+А22-2А1А2cos[π-(α2-α1)]= А12+А22+2А1А2cos(α2-α1)
Начальная фаза φ0 результирующего колебания определяется из ΔОКD
tg 0
KD KC CD A2 sin 2 A1 sin 1
OD OE ED A2 cos 2 A1 cos 1
46.
Сложение колебанийПроанализируем выражение для амплитуды.
А2=А12+А22-2А1А2cos[π-(α2-α1)]= А12+А22+2А1А2cos(α2-α1)
1)Если разность фаз обоих колебаний (φ2- φ1) равна
нулю, амплитуда результирующего колебания равна
сумме А1 и А2.
2) Если разность фаз обоих колебаний (φ2- φ1) равна +π
или – π, т.е. оба колебания находятся в противофазе, то
амплитуда результирующего колебания равна | А1- А2. |.
47.
Сложение колебанийАмплитуда результирующего колебания
зависит от разности фаз φ = φ2 - φ1
складываемых колебаний.
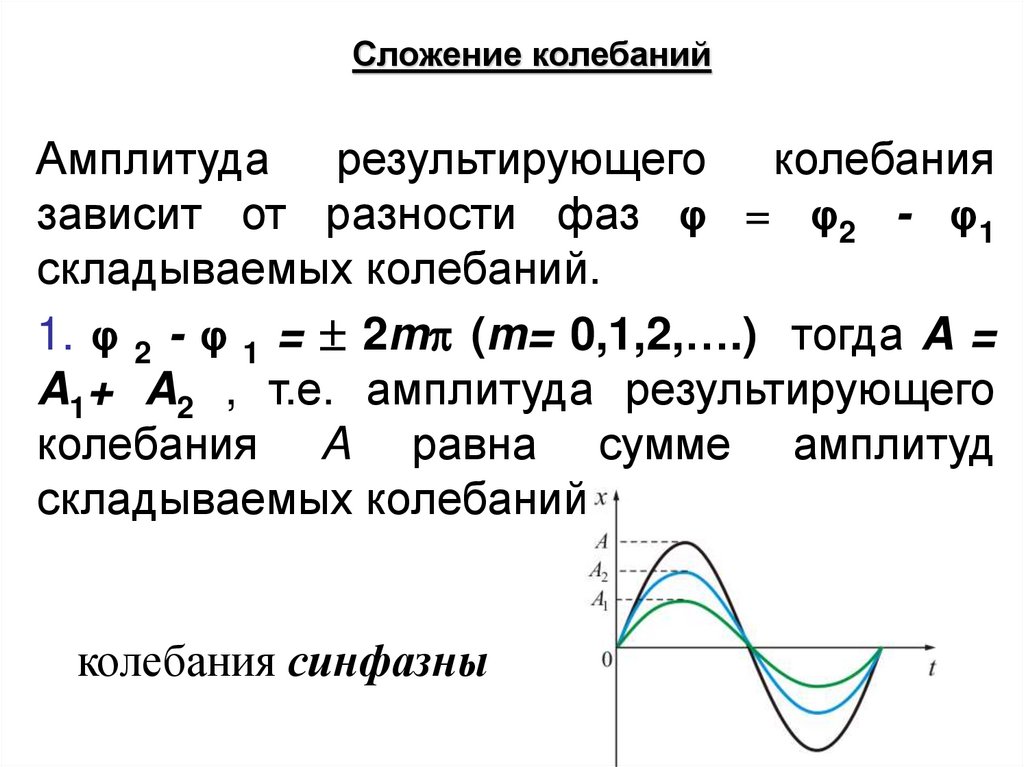
1. φ 2 - φ 1 = 2m (m= 0,1,2,….) тогда A =
A1+ A2 , т.е. амплитуда результирующего
колебания A равна сумме амплитуд
складываемых колебаний;
колебания синфазны
48.
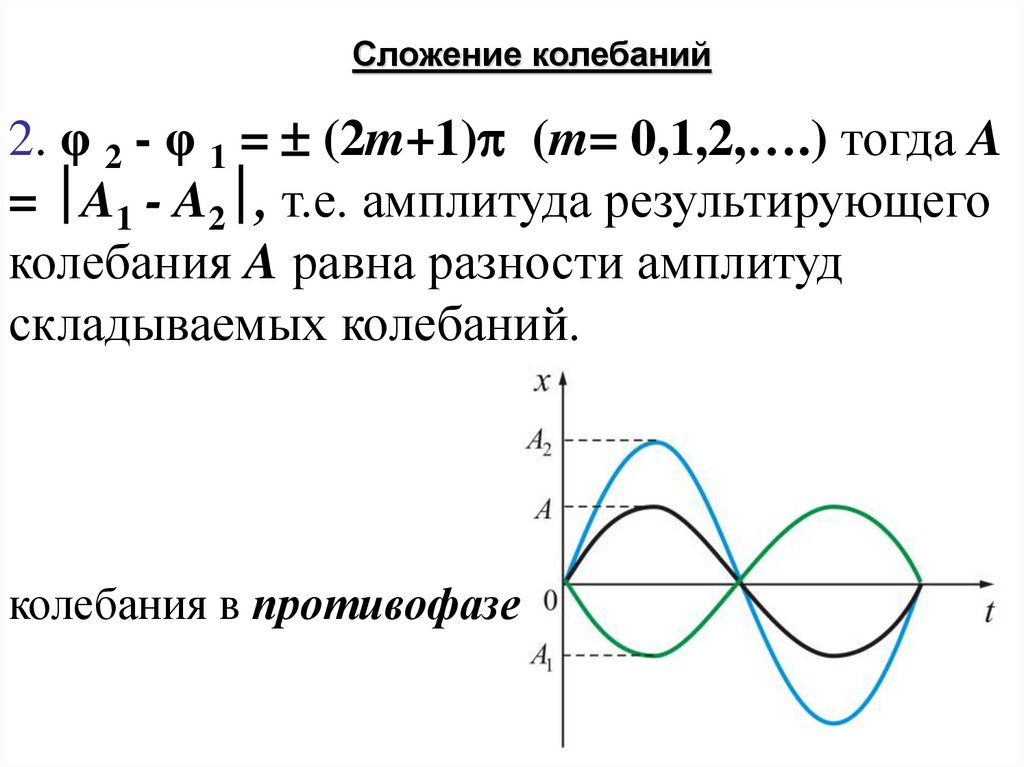
Сложение колебаний2. φ 2 - φ 1 = (2m+1) (m= 0,1,2,….) тогда A
= A1 - A2 , т.е. амплитуда результирующего
колебания A равна разности амплитуд
складываемых колебаний.
колебания в противофазе
49.
БиенияДля практики особый интерес представляет
случай, когда два складываемых колебания
одинакового направления мало отличаются
по частоте. В результате сложения этих
колебаний
получаются
колебания
с
периодически изменяющейся амплитудой.
Периодические
изменения
амплитуды
колебания, возникающие при сложении двух
гармонических колебаний с близкими
частотами, называются БИЕНИЯМИ.
50.
Сумма гармонических колебаний одинакового направления, но разнойчастоты
представляет собой сложное колебание с амплитудой
изменяющейся во времени.
Разность фаз между колебаниями периодически меняется со временем:
1 2 1t 1 2t 2 1 2 t 1 2 const
2 n
В тех интервалах, где колебания близки к синфазным
амплитуда суммарного колебания близка к максимальной:
,
A A1 A2
(2n 1)
В тех интервалах времени, где колебания близки к противофазным
амплитуда суммарного колебания близка к минимальному значению
A A1 A2
50
51. Аналитическое рассмотрение упрощенного случая
Амплитуды и начальные фазы складывающихся колебаний одинаковыA1 A2 A, 1 2 0
1 2
1 2
x(t ) A cos( 1t ) A cos( 2t ) 2 A cos
t cos
t
2
2
Циклические частоты колебаний достаточно близки:
1 2
1,2
x(t ) 2 A(t ) cos( t )
A(t ) A cos( t / 2),
1 2
2
51
52.
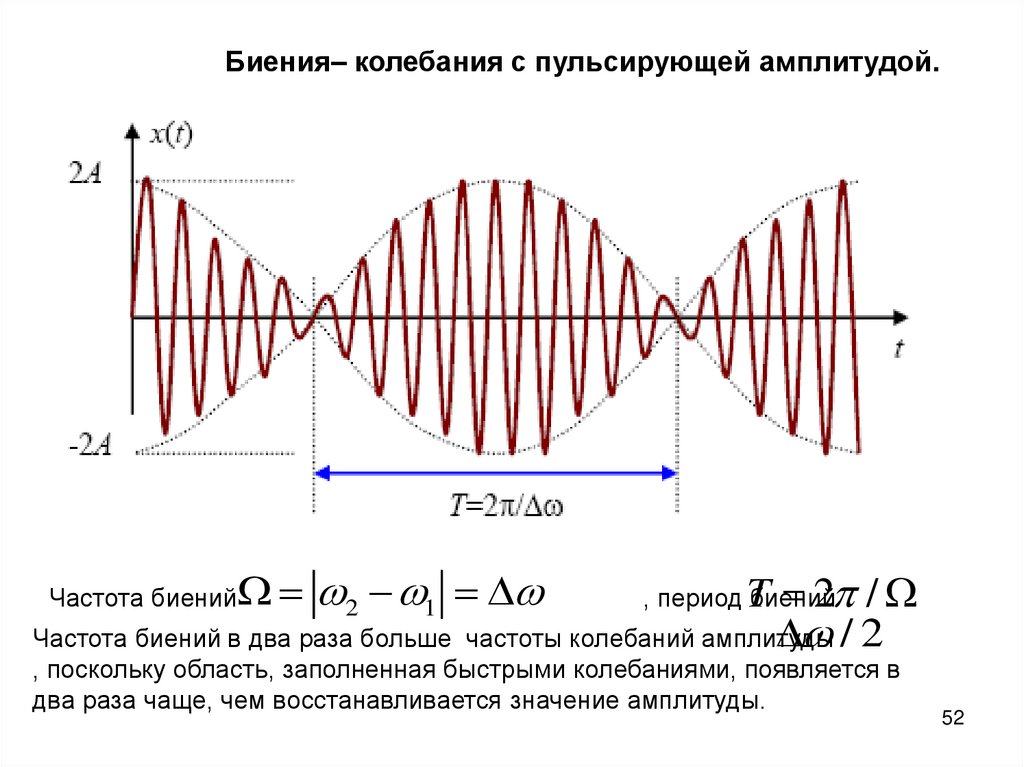
Биения– колебания с пульсирующей амплитудой.2 1
T 2 /
/ 2
Частота биений в два раза больше частоты колебаний амплитуды
Частота биений
, период биений
, поскольку область, заполненная быстрыми колебаниями, появляется в
два раза чаще, чем восстанавливается значение амплитуды.
52
53.
Амплитудабиений
изменяется
вблизи
максимального значения в тех интервалах времени,
когда складывающиеся колебания происходят почти
синфазно:
1 2 t
2 n
1 2
cos
1
2
Амплитуда
биений
изменяется
вблизи
минимального значения в тех интервалах времени,
когда колебания происходят почти в противофазе
друг с другом.
1 2 t (2n 1)
cos
1
2
2
0
53
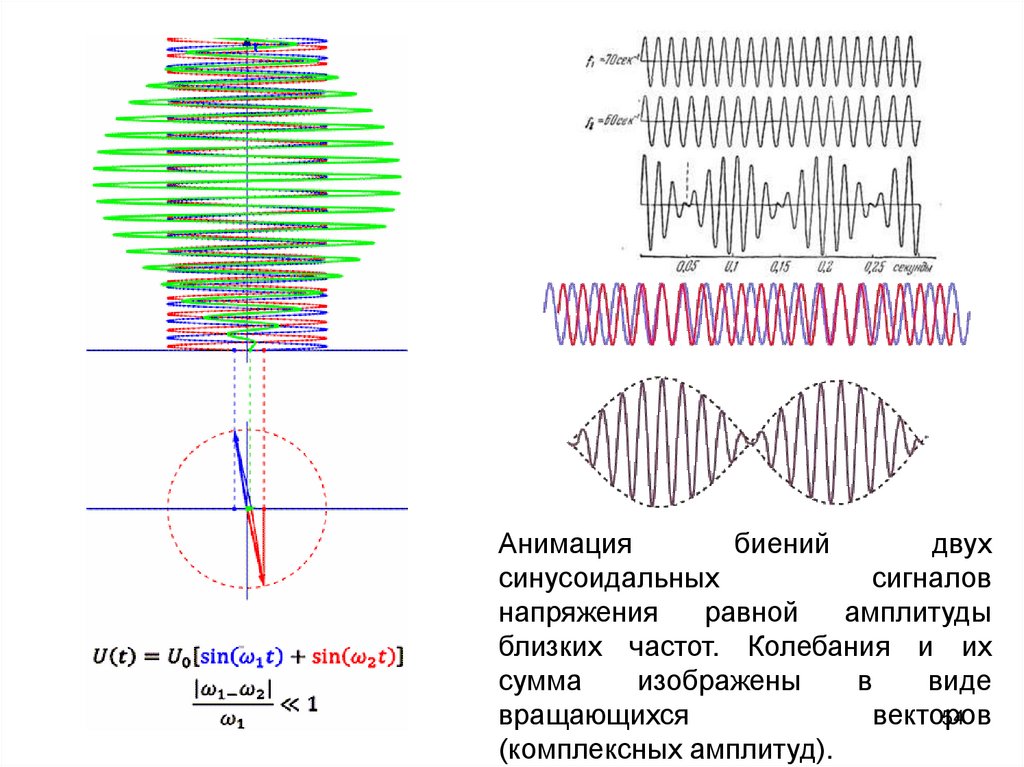
54.
Анимациябиений
двух
синусоидальных
сигналов
напряжения
равной
амплитуды
близких частот. Колебания и их
сумма
изображены
в
виде
вращающихся
векторов
54
(комплексных амплитуд).
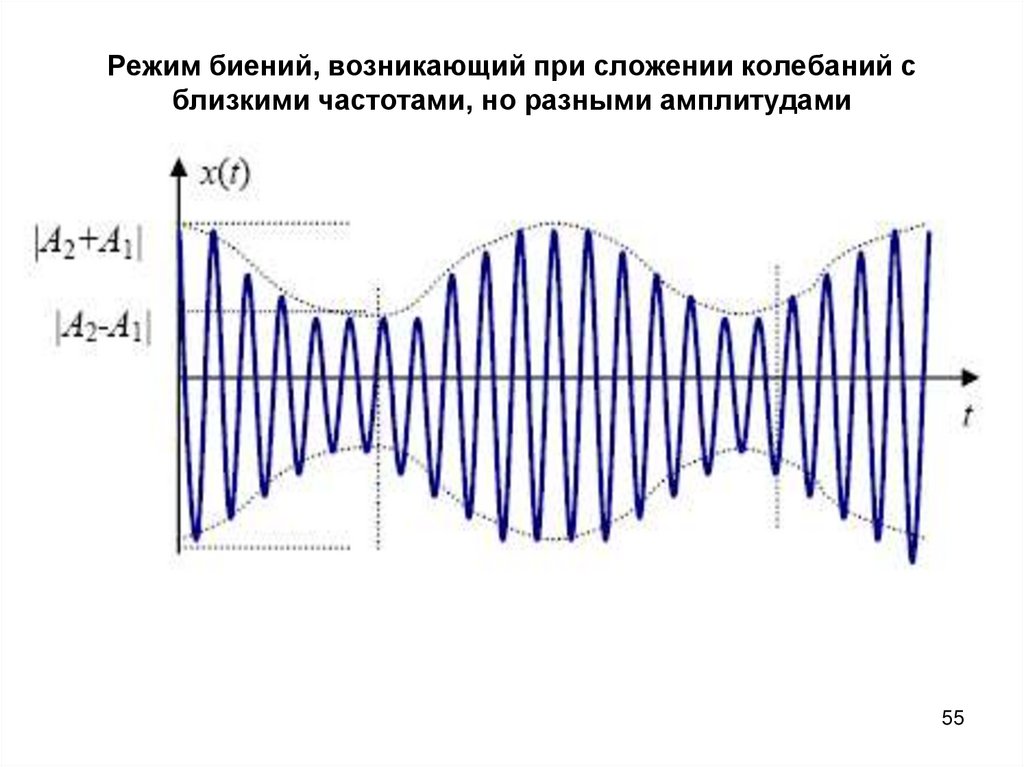
55. Режим биений, возникающий при сложении колебаний с близкими частотами, но разными амплитудами
5556.
В общем случае, колебательноедвижение с изменяющейся во
времени амплитудой называется
колебанием с модулированной
амплитудой.
Быстрая
частота
колебаний называется несущей
частотой,
а
период
между
максимальным
и
минимальным
значением
модулированной
амплитуды – периодом модуляции.
56
57.
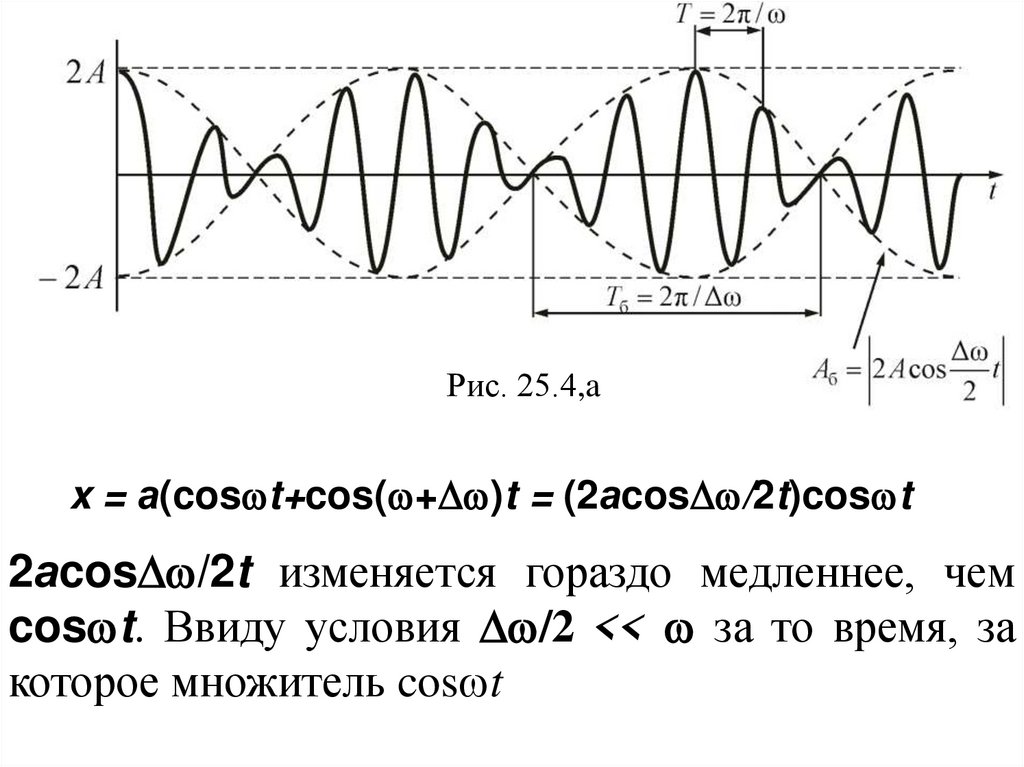
Рис. 25.4,ax = а(cos t+cos( + )t = (2аcos /2t)cos t
2аcos /2t изменяется гораздо медленнее, чем
cos t. Ввиду условия /2 << за то время, за
которое множитель cos t
58.
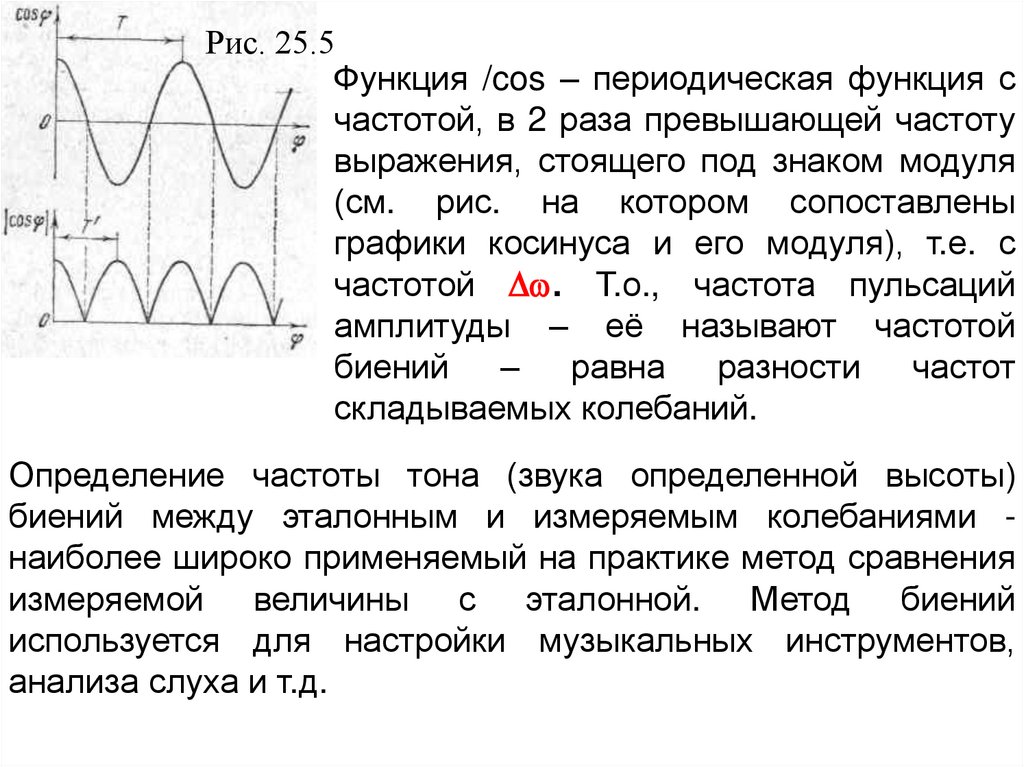
Рис. 25.5Функция /cos – периодическая функция с
частотой, в 2 раза превышающей частоту
выражения, стоящего под знаком модуля
(см. рис. на котором сопоставлены
графики косинуса и его модуля), т.е. с
частотой . Т.о., частота пульсаций
амплитуды – её называют частотой
биений
–
равна
разности
частот
складываемых колебаний.
Определение частоты тона (звука определенной высоты)
биений между эталонным и измеряемым колебаниями наиболее широко применяемый на практике метод сравнения
измеряемой величины с эталонной. Метод биений
используется для настройки музыкальных инструментов,
анализа слуха и т.д.
59.
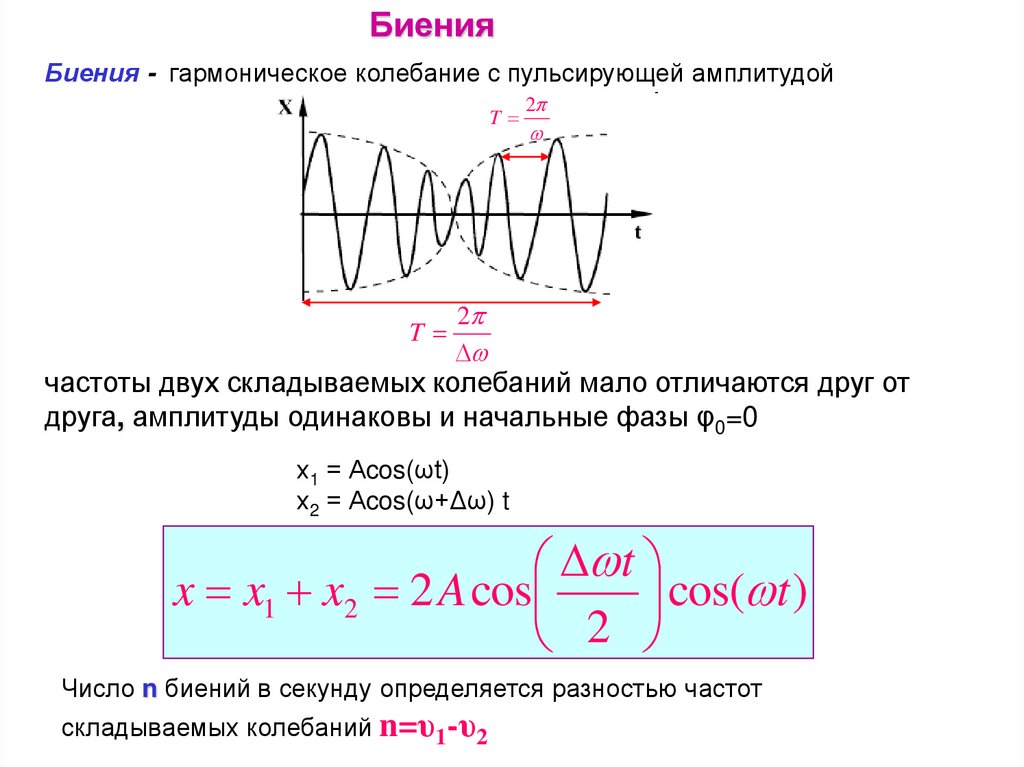
БиенияБиения - гармоническое колебание с пульсирующей амплитудой
T
T
2
2
частоты двух складываемых колебаний мало отличаются друг от
друга, амплитуды одинаковы и начальные фазы φ0=0
х1 = Аcos(ωt)
х2 = Аcos(ω+Δω) t
t
x x1 x2 2 A cos
cos( t )
2
Число n биений в секунду определяется разностью частот
складываемых колебаний n=υ1-υ2
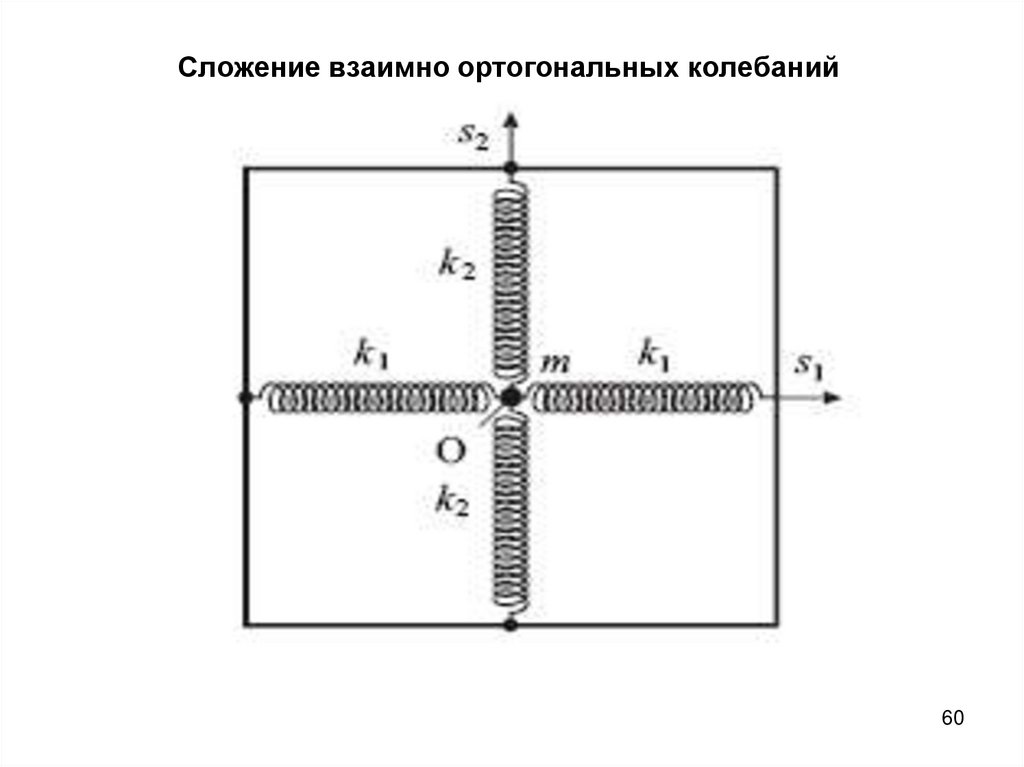
60. Сложение взаимно ортогональных колебаний
6061. Сложение ортогональных колебаний с одинаковыми частотами при различных сдвигах фазы между колебаниями.
s1 x A1 cos t 1s2 y A2 cos t 2
2 1
61
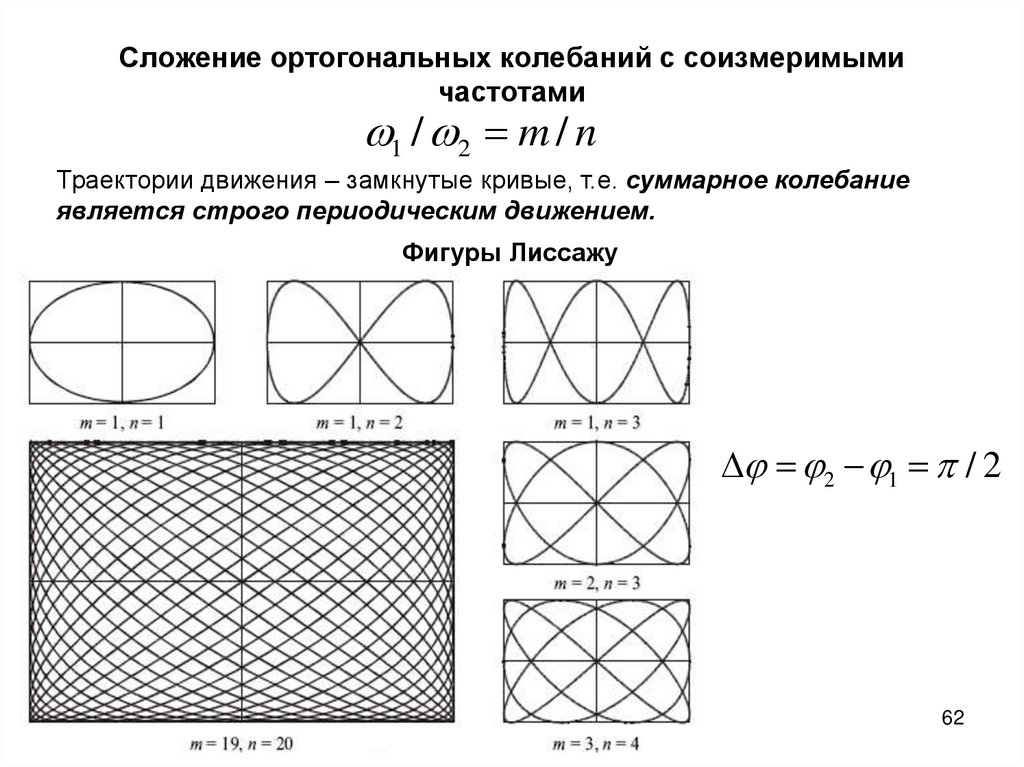
62. Сложение ортогональных колебаний с соизмеримыми частотами
1 / 2 m / nТраектории движения – замкнутые кривые, т.е. суммарное колебание
является строго периодическим движением.
Фигуры Лиссажу
2 1 / 2
62







































 Физика
Физика








