Многомерная оптимизация. Методы градиентного поиска

1.

1

2.

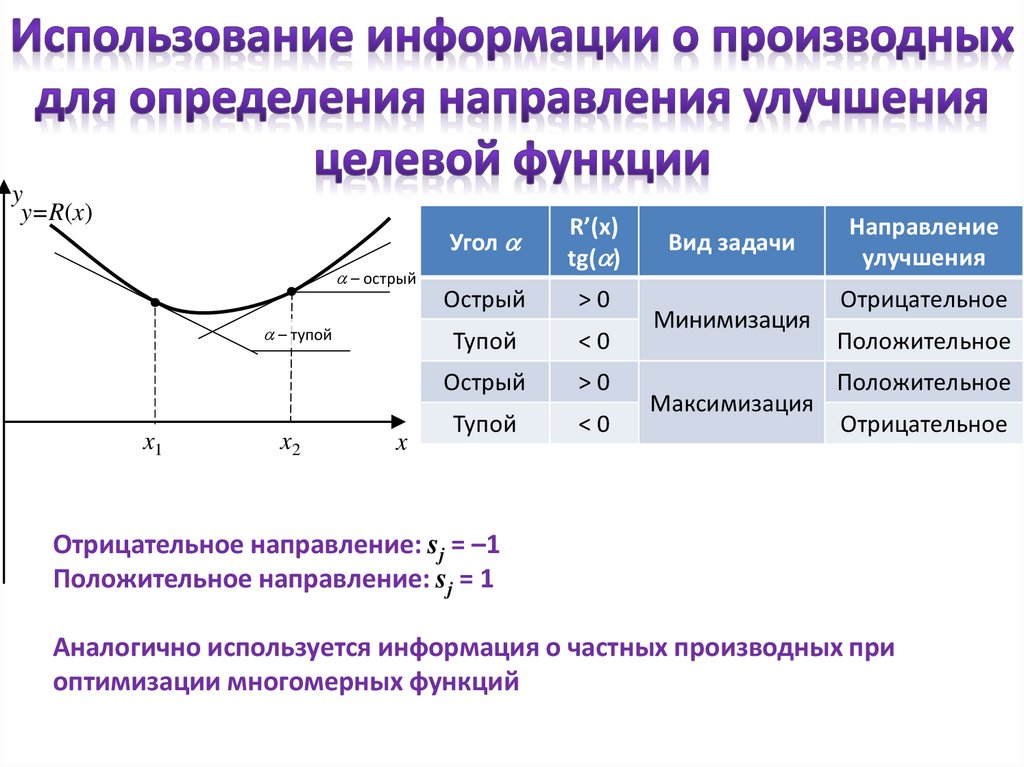
y
y=R(x)
a – острый
a – тупой
x1
x2
x
Угол a
R’(x)
tg(a)
Острый
>0
Тупой
<0
Острый
>0
Тупой
<0
Вид задачи
Минимизация
Максимизация
Направление
улучшения
Отрицательное
Положительное
Положительное
Отрицательное
Отрицательное направление: sj = –1
Положительное направление: sj = 1
Аналогично используется информация о частных производных при
оптимизации многомерных функций

3.

1. Задаются:
0
– начальная точка поиска оптимума x
– начальный шаг поиска h(0) и точность e.
2. Рассчитываются значения частных
производных по всем переменным, кроме
последней использовавшейся. С учётом вида
задачи по величине (наибольшей по модулю) и
знаку частной производной определяется
переменная j и знак осевого направления sj
наискорейшего улучшения целевой функции.
3. Из последней лучшей точки выполняется последовательность шагов в
выбранном направлении оси j до тех пор, пока целевая функция R продолжает
k 1
улучшаться: x j
x jk s j h q
4. Если выбор ни одной новой переменной после расчёта частных производных
не привёл к улучшению целевой функции, проверяется выполнение условия
q
окончания: h e . Если оно выполняется, вычисления заканчиваются.
Решение – последняя лучшая точка.
q 1
Иначе уменьшается шаг поиска: h
h q K
3
K – кратность уменьшения шага (обычно от 2 до 10, целесообразно: 3, 5, 7).
Возврат к п. 2

4.

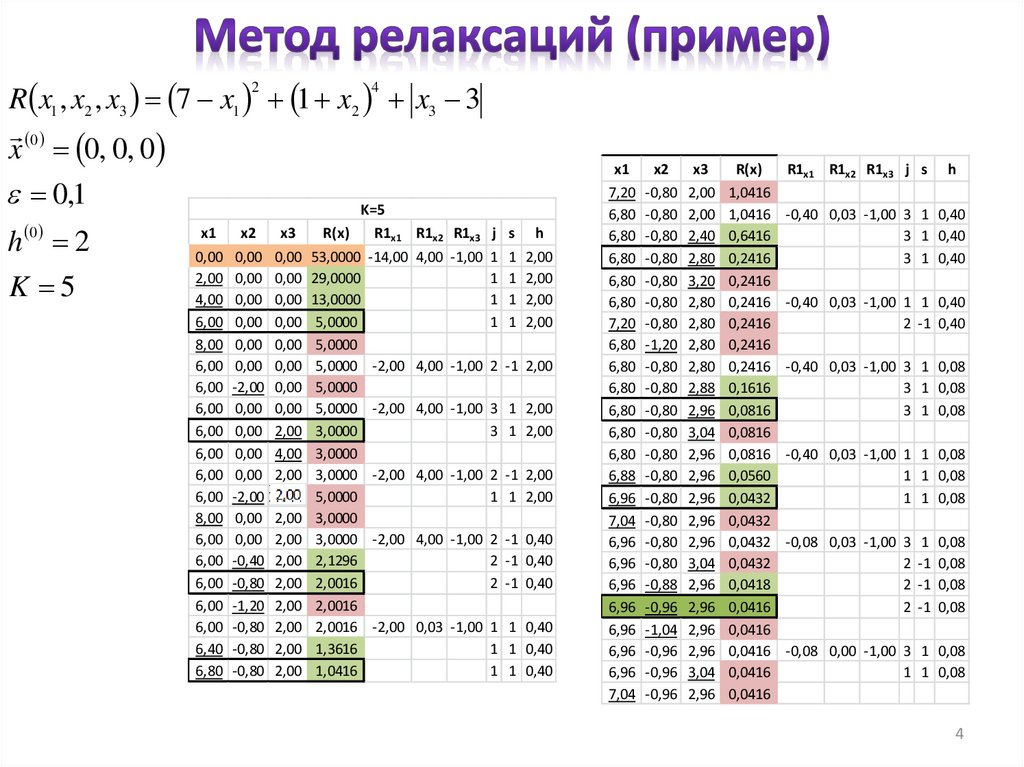
R x1 , x2 , x3 7 x1 1 x2 x3 3
0
x 0, 0, 0
e 0,1
K=5
2
0
h 2
K 5
4
x1 x2 x3
R(x)
R1x1 R1x2 R1x3 j s h
0,00 0,00 0,00 53,0000 -14,00 4,00 -1,00 1 1 2,00
2,00 0,00 0,00 29,0000
1 1 2,00
4,00 0,00 0,00 13,0000
1 1 2,00
6,00 0,00 0,00 5,0000
1 1 2,00
8,00 0,00 0,00 5,0000
6,00 0,00 0,00 5,0000 -2,00 4,00 -1,00 2 -1 2,00
6,00 -2,00 0,00 5,0000
6,00 0,00 0,00 5,0000 -2,00 4,00 -1,00 3 1 2,00
6,00 0,00 2,00 3,0000
3 1 2,00
6,00 0,00 4,00 3,0000
6,00 0,00 2,00 3,0000 -2,00 4,00 -1,00 2 -1 2,00
6,00 -2,00 0,00 5,0000
1 1 2,00
8,00 0,00 2,00 3,0000
6,00 0,00 2,00 3,0000 -2,00 4,00 -1,00 2 -1 0,40
6,00 -0,40 2,00 2,1296
2 -1 0,40
6,00 -0,80 2,00 2,0016
2 -1 0,40
6,00 -1,20 2,00 2,0016
6,00 -0,80 2,00 2,0016 -2,00 0,03 -1,00 1 1 0,40
6,40 -0,80 2,00 1,3616
1 1 0,40
6,80 -0,80 2,00 1,0416
1 1 0,40
x1 x2 x3
7,20 -0,80 2,00
6,80 -0,80 2,00
6,80 -0,80 2,40
6,80 -0,80 2,80
6,80 -0,80 3,20
6,80 -0,80 2,80
7,20 -0,80 2,80
6,80 -1,20 2,80
6,80 -0,80 2,80
6,80 -0,80 2,88
6,80 -0,80 2,96
6,80 -0,80 3,04
6,80 -0,80 2,96
6,88 -0,80 2,96
6,96 -0,80 2,96
7,04 -0,80 2,96
6,96 -0,80 2,96
6,96 -0,80 3,04
6,96 -0,88 2,96
6,96 -0,96 2,96
6,96 -1,04 2,96
6,96 -0,96 2,96
6,96 -0,96 3,04
7,04 -0,96 2,96
R(x)
1,0416
1,0416
0,6416
0,2416
0,2416
0,2416
0,2416
0,2416
0,2416
0,1616
0,0816
0,0816
0,0816
0,0560
0,0432
0,0432
0,0432
0,0432
0,0418
0,0416
0,0416
0,0416
0,0416
0,0416
R1x1 R1x2 R1x3 j s
h
-0,40 0,03 -1,00 3 1 0,40
3 1 0,40
3 1 0,40
-0,40 0,03 -1,00 1 1 0,40
2 -1 0,40
-0,40 0,03 -1,00 3 1 0,08
3 1 0,08
3 1 0,08
-0,40 0,03 -1,00 1 1 0,08
1 1 0,08
1 1 0,08
-0,08 0,03 -1,00 3 1 0,08
2 -1 0,08
2 -1 0,08
2 -1 0,08
-0,08 0,00 -1,00 3 1 0,08
1 1 0,08
4

5.

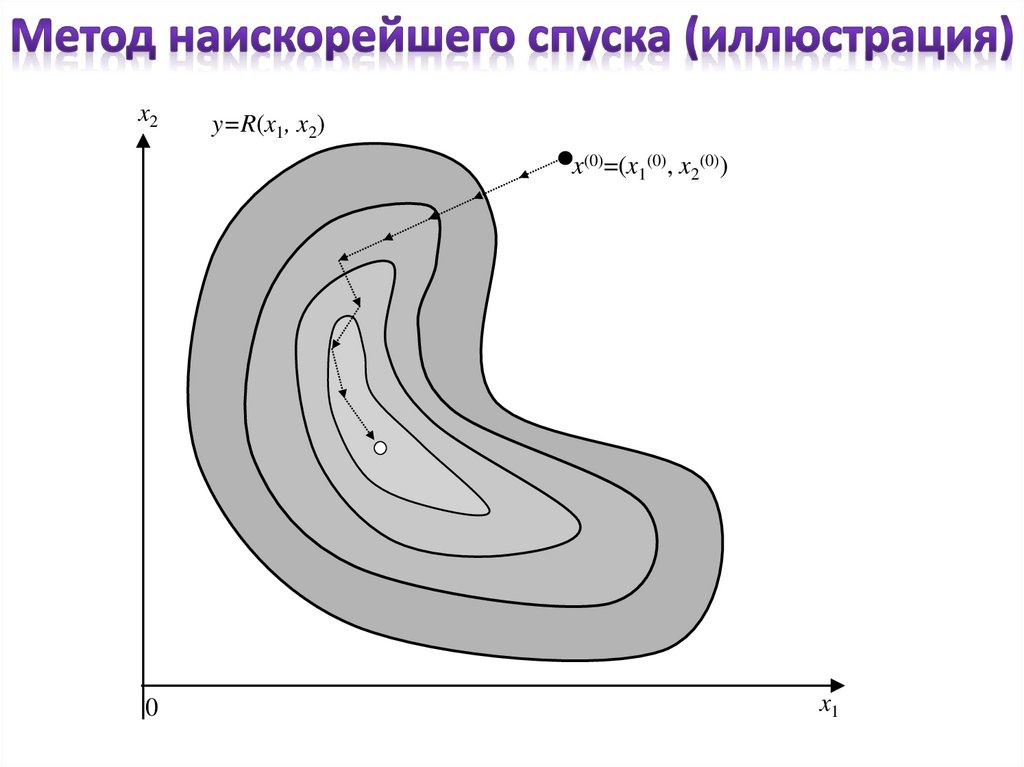
x2
y=R(x1, x2)
x(0)=(x1(0), x2(0))
0
x1

6.

1. Задаются:
0
– начальная точка поиска оптимума x
– начальный шаг поиска h(0) и точность e.
2. Рассчитываются значения частных
производных по всем N переменным и
координаты градиента в последней лучшей (или
R
начальной) точке:
j
x j
R
i 1 xi
2
N
3. Из последней лучшей точки выполняется шаг в направлении оптимума:
x jk 1 x jk j h q – для минимизации и x jk 1 x jk j h q – для
максимизации. Рассчитывается значение критерия R в новой точке.
4. Если значение критерия R в новой точке лучше, чем в последней лучшей
точке, новая точка запоминается как лучшая, и возврат к п. 2.
q
Иначе проверяется условие окончания вычислений h e .
5. Если условие окончания выполняется, вычисления заканчиваются. Решение
– последняя лучшая точка. Иначе уменьшается шаг поиска: h q 1 h q K
6
K – кратность уменьшения шага (обычно от 2 до 10).
Возврат к п. 2

7.

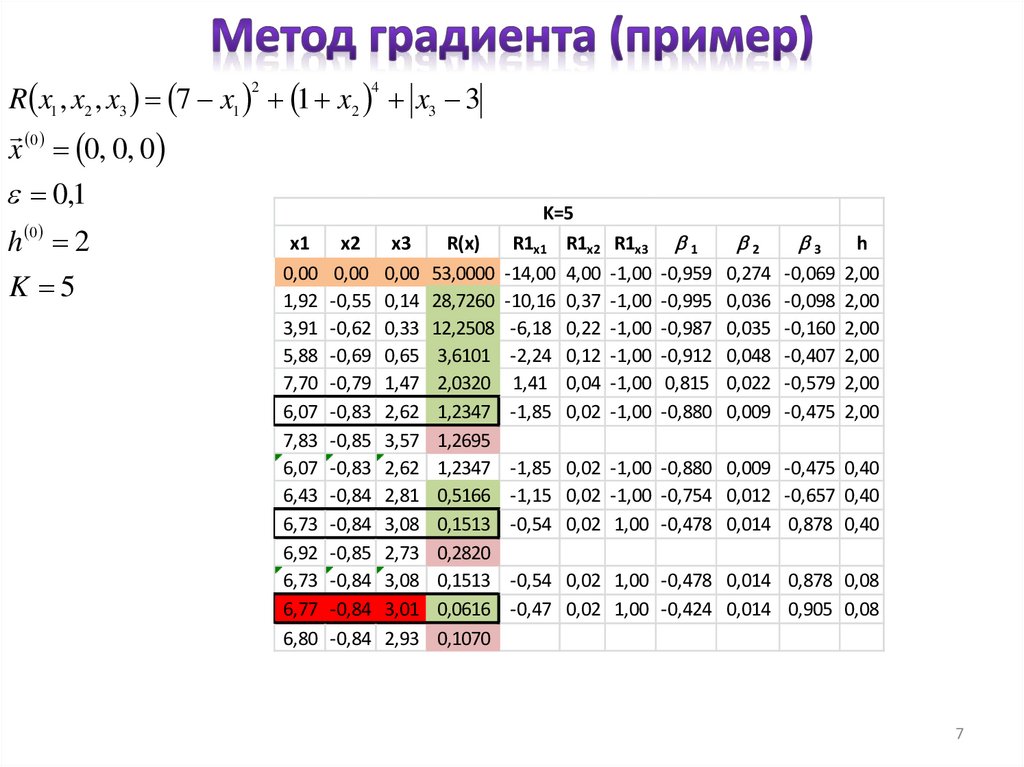
R x1 , x2 , x3 7 x1 1 x2 x3 3
0
x 0, 0, 0
e 0,1
2
0
h 2
K 5
4
K=5
x1 x2 x3
R(x)
R1x1 R1x2 R1x3 1
2
3
h
0,00 0,00 0,00 53,0000 -14,00 4,00 -1,00 -0,959 0,274 -0,069 2,00
1,92 -0,55 0,14 28,7260 -10,16 0,37 -1,00 -0,995 0,036 -0,098 2,00
3,91 -0,62 0,33 12,2508 -6,18 0,22 -1,00 -0,987 0,035 -0,160 2,00
5,88 -0,69 0,65 3,6101 -2,24 0,12 -1,00 -0,912 0,048 -0,407 2,00
7,70 -0,79 1,47 2,0320 1,41 0,04 -1,00 0,815 0,022 -0,579 2,00
6,07 -0,83 2,62 1,2347 -1,85 0,02 -1,00 -0,880 0,009 -0,475 2,00
7,83 -0,85 3,57 1,2695
6,07 -0,83 2,62 1,2347 -1,85 0,02 -1,00 -0,880 0,009 -0,475 0,40
6,43 -0,84 2,81 0,5166 -1,15 0,02 -1,00 -0,754 0,012 -0,657 0,40
6,73 -0,84 3,08 0,1513 -0,54 0,02 1,00 -0,478 0,014 0,878 0,40
6,92 -0,85 2,73 0,2820
6,73 -0,84 3,08 0,1513 -0,54 0,02 1,00 -0,478 0,014 0,878 0,08
6,77 -0,84 3,01 0,0616 -0,47 0,02 1,00 -0,424 0,014 0,905 0,08
6,80 -0,84 2,93 0,1070
7

8.

x2
y=R(x1, x2)
x(0)=(x1(0), x2(0))
0
x1

9.

1. Задаются:
0
– начальная точка поиска оптимума x
– начальный шаг поиска h(0) и точность e.
2. Рассчитываются значения частных
производных по всем N переменным и
координаты градиента в последней лучшей (или
R
начальной) точке:
j
x j
R
i 1 xi
2
N
3. Из последней лучшей точки выполняется серия шагов в направлении
улучшения целевой функции: x jk 1 x jk j h q – для минимизации,
x jk 1 x jk j h q – для максимизации до тех пор, пока продолжает
улучшаться значение критерия R. Если улучшение ни разу не произошло, шаг
поиска уменьшается: h q 1 h q K , K – кратность уменьшения шага (обычно от
2 до 10). Затем возврат к п. 2.
4. Если значение критерия R ухудшилось после хотя бы одного удачного шага,
q
проверяется условие окончания вычислений h e . Если оно выполняется,
9
вычисления заканчиваются. Решение – последняя лучшая точка.
Иначе возврат к п. 2 без изменения размера шага.

10.

R x1 , x2 , x3 7 x1 1 x2 x3 3
0
x 0, 0, 0
e 0,1
2
h 0 2
K 5
4
K=5
x1 x2 x3
R(x)
R1x1 R1x2 R1x3 1
2
3
h
0,00 0,00 0,00 53,0000 -14,00 4,00 -1,00 -0,959 0,274 -0,069 2,00
1,92 -0,55 0,14 28,7260 -14,00 4,00 -1,00 -0,959 0,274 -0,069 2,00
3,84 -1,10 0,27 12,7302 -14,00 4,00 -1,00 -0,959 0,274 -0,069 2,00
5,76 -1,64 0,41 4,3099 -14,00 4,00 -1,00 -0,959 0,274 -0,069 2,00
7,67 -2,19 0,55 4,9292
5,76 -1,64 0,41 4,3099 -2,49 -1,07 -1,00 -0,862 -0,371 -0,346 2,00
7,48 -0,90 1,10 2,1260 -2,49 -1,07 -1,00 -0,862 -0,371 -0,346 2,00
9,20 -0,16 1,80 6,5499
7,48 -0,90 1,10 2,1260 0,96 0,00 -1,00 0,692 0,003 -0,722 2,00
6,10 -0,91 2,55 1,2708 0,96 0,00 -1,00 0,692 0,003 -0,722 2,00
4,71 -0,91 3,99 6,2285
6,10 -0,91 2,55 1,2708 -1,81 0,00 -1,00 -0,875 0,001 -0,484 2,00
7,85 -0,91 3,52 1,2305 -1,81 0,00 -1,00 -0,875 0,001 -0,484 2,00
9,60 -0,91 4,48 8,2230
7,85 -0,91 3,52 1,2305 1,69 0,00 1,00 0,861 0,001 0,509 2,00
6,12 -0,91 2,50 1,2699
7,85 -0,91 3,52 1,2305 1,69 0,00 1,00 0,861 0,001 0,509 0,40
7,50 -0,91 3,31 0,5631 1,69 0,00 1,00 0,861 0,001 0,509 0,40
7,16 -0,91 3,11 0,1327 1,69 0,00 1,00 0,861 0,001 0,509 0,40
6,81 -0,91 2,90 0,1307 1,69 0,00 1,00 0,861 0,001 0,509 0,40
6,47 -0,91 2,70 0,5817
6,81 -0,91 2,90 0,1307 -0,37 0,00 -1,00 -0,351 0,002 -0,937 0,40
6,95 -0,91 3,28 0,2813
6,81 -0,91 2,90 0,1307 -0,37 0,00 -1,00 -0,351 0,002 -0,937 0,08
6,84 -0,91 2,98 0,0460 -0,37 0,00 -1,00 -0,351 0,002 -0,937 0,08
6,87 -0,91 3,05 0,0715
6,84 -0,91 2,98 0,0460 -0,32 0,00 -1,00 -0,303 0,002 -0,953 0,08
6,87 -0,91 3,06 0,0738
10

11.

x2
y=R(x1, x2)
x(0)=(x1(0), x2(0))
метод градиента
метод релаксаций
метод наискорейшего спуска
0
x1

12.

1. Возможность остановки поиска решения в локальной точке оптимума
целевой функции
2. Вероятна недостижимость решения с требуемой точностью для не
дифференцируемых целевых функций
1. Решение задачи с использованием различных начальных
приближений
2. Использование методов оптимизации, основанных на других
принципах приближения к оптимуму
12

13.

13

14.

Метод случайных направлений
1. Поиск нового случайного направления улучшения целевой функции в
каждой новой точке
Метод случайных направлений с обратным шагом
1. Поиск нового случайного направления улучшения целевой функции в
каждой новой точке
2. Попытка поиска в противоположном направлении в случае
неудачного нового направления
Метод спуска с наказанием случайностью
1. Поиск нового случайного направления улучшения целевой функции в
каждой новой точке
2. Попытка поиска в противоположном направлении в случае
неудачного нового направления
3. Движение вдоль последнего направления улучшения целевой
функции, пока она продолжает улучшаться

15.

x2
y=R(x1, x2)
x(0)=(x1(0), x2(0))
0
x1

16.

1. Задаются:
0
– начальная точка поиска оптимума x
– начальный шаг поиска h(0) и точность e и
предельное количество неудачных попыток M.
2. Случайным образом генерируются N чисел из
симметричного относительно начала отсчёта
диапазона: [–a; a].
3. Рассчитываются координаты
случайного
aj
направления: j N
a
i 1
2
i
4. Из последней лучшей точки выполняется серия шагов в случайном
направлении: x jk 1 x jk j h q до тех пор, пока продолжает улучшаться
значение критерия R. Если улучшение ни разу не произошло, делается попытка
выполнить удачную серию в обратном направлении: x jk 1 x jk j h q .
5. Если прямое и обратное направления ни разу не дали улучшение критерия,
счётчик неудачных попыток увеличивается на 1 и возврат к п. 2.
6. Если выполнено M неудачных попыток, проверяется условие окончания
16
h q e . Если оно выполняется, вычисления заканчиваются, иначе шаг поиска
уменьшается h q 1 h q K и возврат к п. 2.

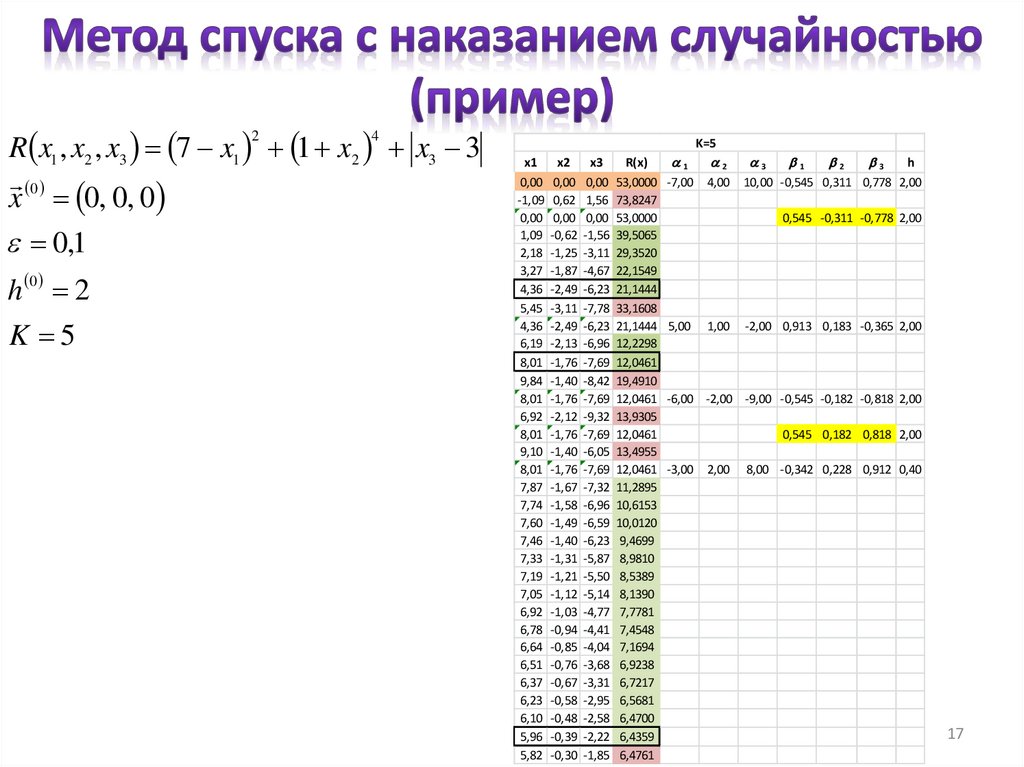
17.

R x1 , x2 , x3 7 x1 1 x2 x3 3
x 0 0, 0, 0
e 0,1
2
h 0 2
K 5
4
K=5
x1 x2 x3
R(x)
a1
a2
0,00 0,00 0,00 53,0000 -7,00 4,00
-1,09 0,62 1,56 73,8247 -7,00 4,00
0,00 0,00 0,00 53,0000
1,09 -0,62 -1,56 39,5065
2,18 -1,25 -3,11 29,3520
3,27 -1,87 -4,67 22,1549
4,36 -2,49 -6,23 21,1444
5,45 -3,11 -7,78 33,1608
4,36 -2,49 -6,23 21,1444 5,00 1,00
6,19 -2,13 -6,96 12,2298
8,01 -1,76 -7,69 12,0461
9,84 -1,40 -8,42 19,4910
8,01 -1,76 -7,69 12,0461 -6,00 -2,00
6,92 -2,12 -9,32 13,9305
8,01 -1,76 -7,69 12,0461
9,10 -1,40 -6,05 13,4955
8,01 -1,76 -7,69 12,0461 -3,00 2,00
7,87 -1,67 -7,32 11,2895
7,74 -1,58 -6,96 10,6153
7,60 -1,49 -6,59 10,0120
7,46 -1,40 -6,23 9,4699
7,33 -1,31 -5,87 8,9810
7,19 -1,21 -5,50 8,5389
7,05 -1,12 -5,14 8,1390
6,92 -1,03 -4,77 7,7781
6,78 -0,94 -4,41 7,4548
6,64 -0,85 -4,04 7,1694
6,51 -0,76 -3,68 6,9238
6,37 -0,67 -3,31 6,7217
6,23 -0,58 -2,95 6,5681
6,10 -0,48 -2,58 6,4700
5,96 -0,39 -2,22 6,4359
5,82 -0,30 -1,85 6,4761
a3
1
2
3
h
10,00 -0,545 0,311 0,778 2,00
10,00 -0,545 0,311 0,778 2,00
0,545 -0,311 -0,778 2,00
0,545 -0,311 -0,778 2,00
0,545 -0,311 -0,778 2,00
0,545 -0,311 -0,778 2,00
0,545 -0,311 -0,778 2,00
-2,00 0,913 0,183 -0,365 2,00
0,913 0,183 -0,365 2,00
0,913 0,183 -0,365 2,00
-9,00 -0,545 -0,182 -0,818 2,00
0,545 0,182 0,818 2,00
8,00 -0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
-0,342 0,228
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
0,912 0,40
17

18.

1. Большое количество шагов вычислений
2. Большой объём вычислений
3. Продолжительное время поиска решения
1. Возможность поиска решения для функций со сложным рельефом
поверхности
2. Не нужно численно рассчитывать частные производные
18

19.

Определить тип задачи многомерной оптимизации и решить её методами
релаксаций, градиента, наискорейшего спуска, спуска с наказанием
случайностью. N – номер варианта лабораторного практикума.