Похожие презентации:
Тетраэдр и параллелепипед
1.
Тетраэдр ипараллелепипед
2. Понятие тетраэдра
Элементы тетраэдраГрани (4)
Вершины (4)
S
Ребра (6)
Основание
А
С
В
3. Элементы тетраэдра
параллелепипед4.
Наклонный параллелепипедПараллелепипед (от греч. παράλλος − параллельный и
греч. επιπεδον − плоскость) − призма, основанием которой
служит параллелограмм, или многогранник, у которого
шесть граней и каждая из них − параллелограмм.
5. параллелепипед
Основания (2)Ребра (12)
Вершины (8)
Боковые грани (4)
6.
Параллелепипед ABCDA1B1C1D1D1
C1
А1
B1
С
D
А
В
7.
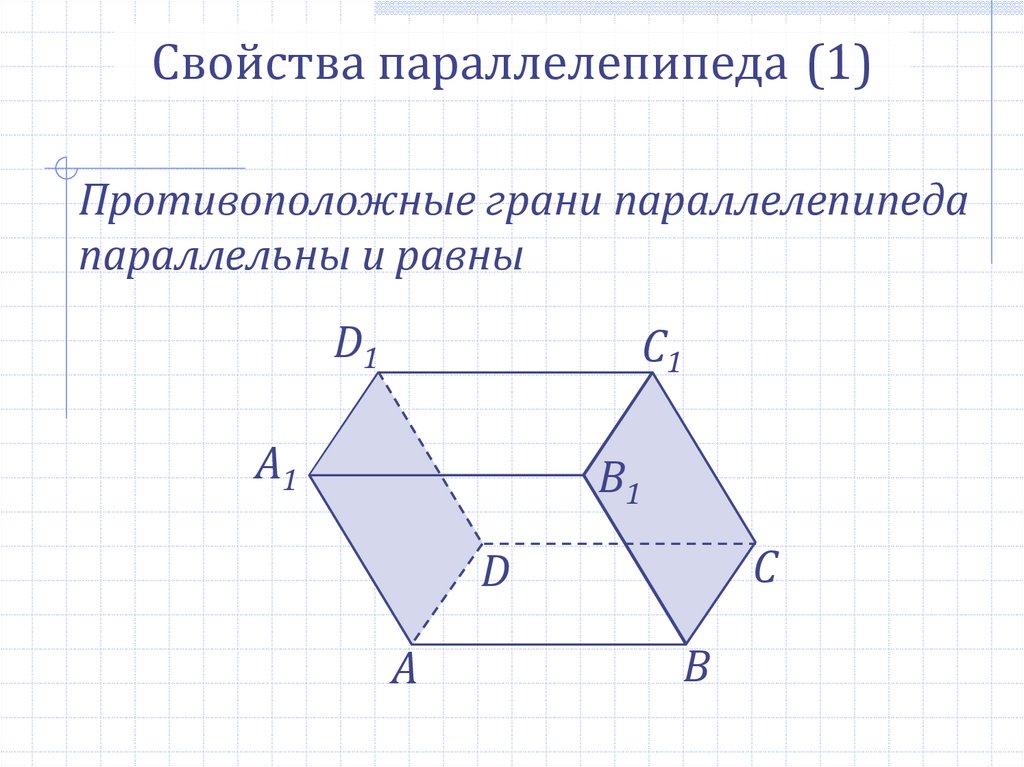
Свойства параллелепипеда (1)Противоположные грани параллелепипеда
параллельны и равны
D1
C1
А1
B1
С
D
А
В
8.
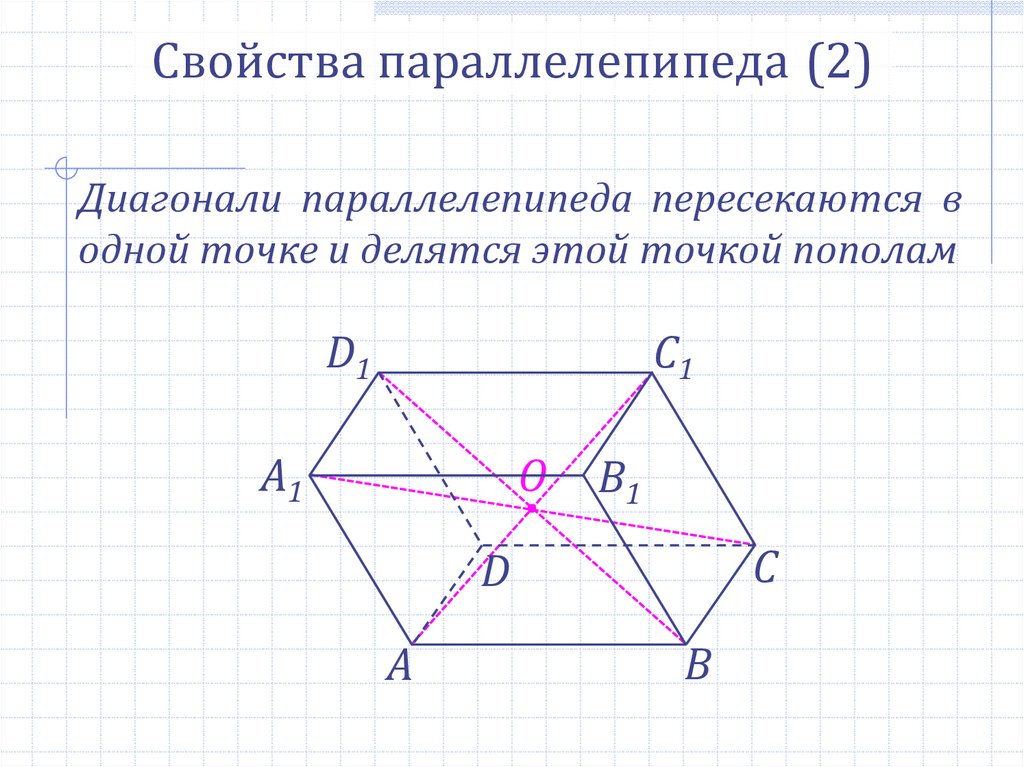
Свойства параллелепипеда (2)Диагонали параллелепипеда пересекаются в
одной точке и делятся этой точкой пополам
D1
C1
А1
О
B1
С
D
А
В
9.
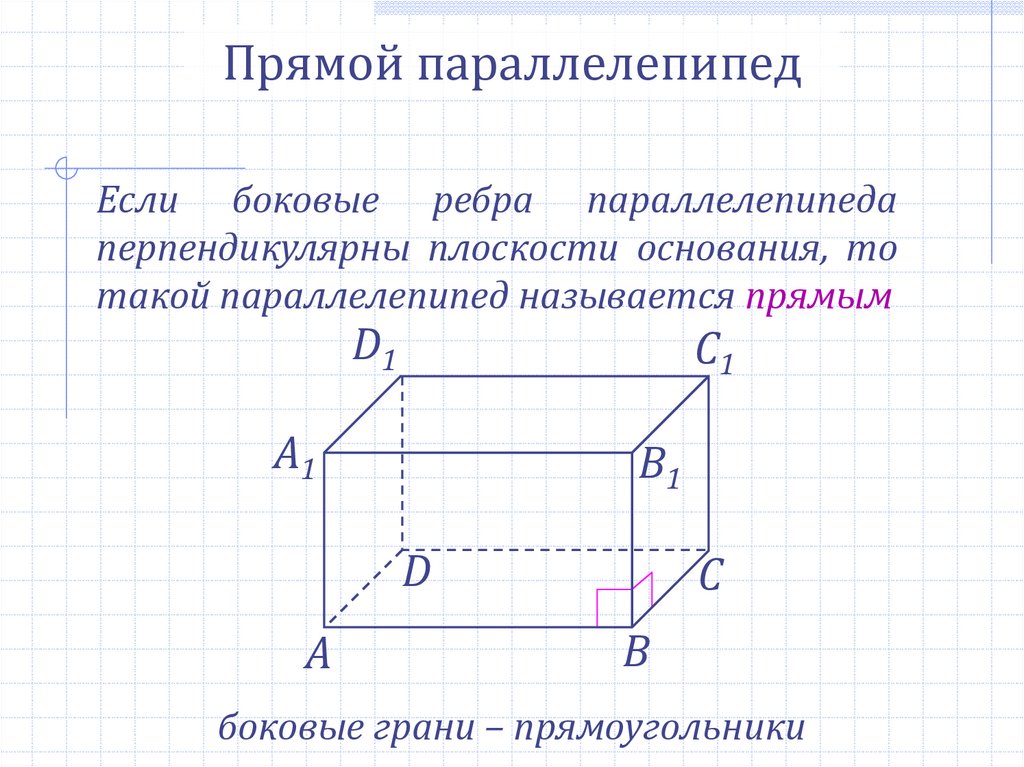
Прямой параллелепипедЕсли боковые ребра параллелепипеда
перпендикулярны плоскости основания, то
такой параллелепипед называется прямым
D1
C1
А1
B1
D
А
С
В
боковые грани – прямоугольники
10.
Прямоугольный параллелепипедПрямой параллелепипед, основания которого
являются
прямоугольниками
называется
прямоугольным
D1
C1
А1
B1
D
А
С
В
все грани – прямоугольники
11.
Свойства прямоугольногопараллелепипеда
1° В прямоугольном параллелепипеде все
шесть граней – прямоугольники
2° Все двугранные углы прямоугольного
параллелепипеда– прямые
12.
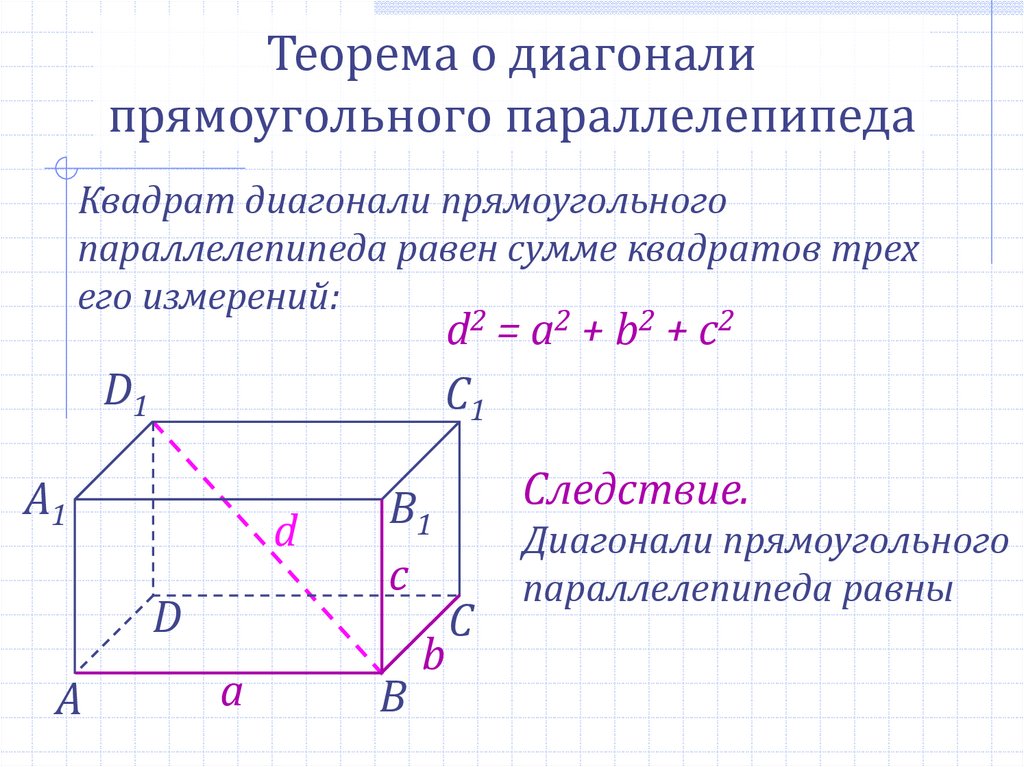
Теорема о диагоналипрямоугольного параллелепипеда
Квадрат диагонали прямоугольного
параллелепипеда равен сумме квадратов трех
его измерений:
d2 = a2 + b2 + c2
C1
D1
А1
d
D
А
a
B1
c
В
b
Следствие.
С
Диагонали прямоугольного
параллелепипеда равны
13.
КубПрямоугольный параллелепипед, все грани
которого – равные квадраты называется кубом
d
a
a
a
d2 = 3a2
все грани – равные квадраты
14.
Многоугольник, сторонамикоторого являются отрезки,
по которым секущая
плоскость пересекает грани
тетраэдра, называется
сечением тетраэдра.
Тетраэдр
15.
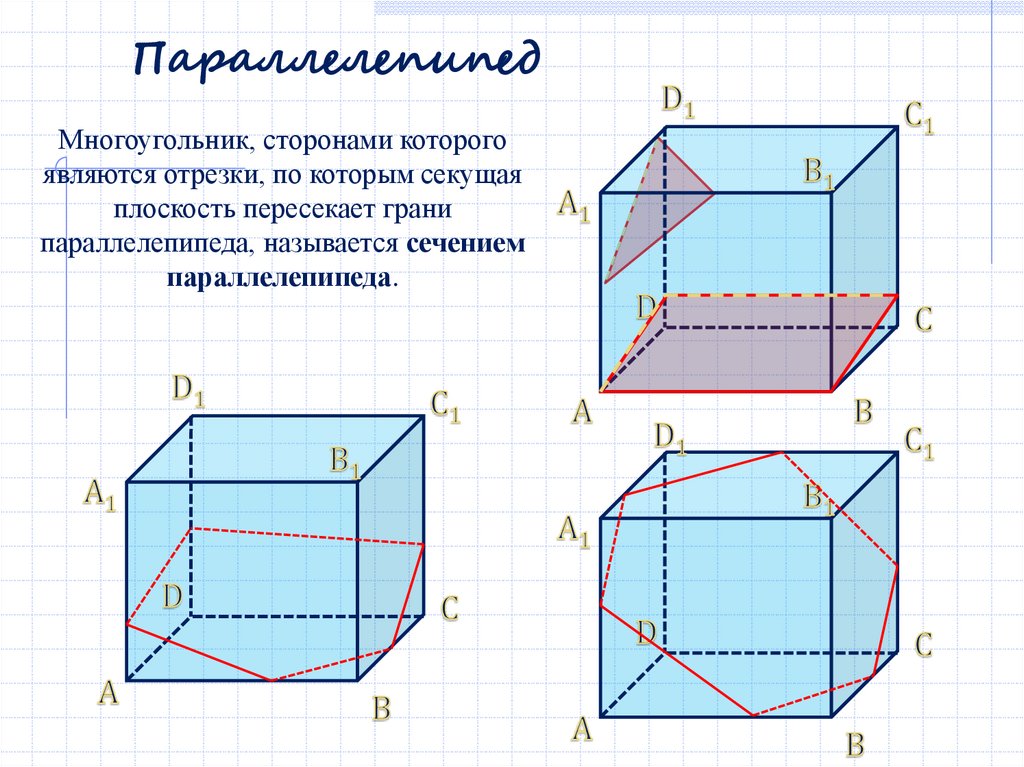
ПараллелепипедМногоугольник, сторонами которого
являются отрезки, по которым секущая
плоскость пересекает грани
параллелепипеда, называется сечением
параллелепипеда.
16.
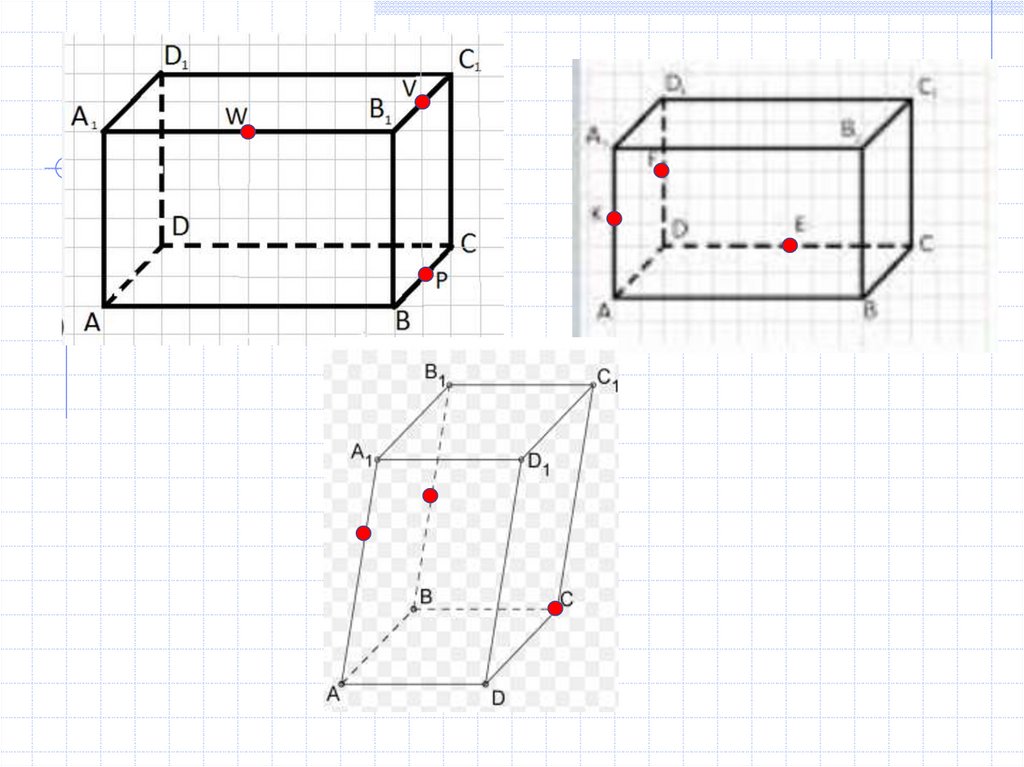
Д/з построить сечения по точкамСложное *










 Математика
Математика








