Тетраэдр и параллелепипед

1. Тетраэдр и параллелепипед

ТЕТРАЭДР И ПАРАЛЛЕЛЕПИПЕД

2.

3.

Тетраэдр
Поверхность, составленная
из четырёх треугольников
ABC, DAB, DBC и DCA,
называется тетраэдром и
обозначается DABC.
Тетраэдр имеет 4 грани, 6
рёбер и 4 вершины.

4.

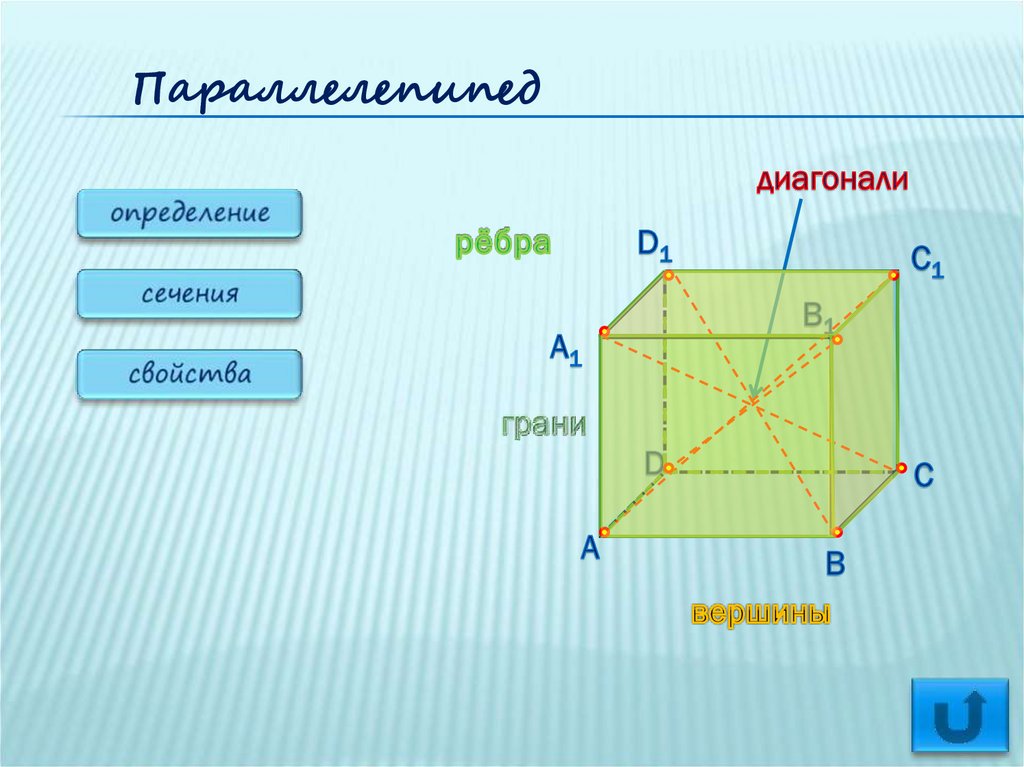
Параллелепипед
D1
A1
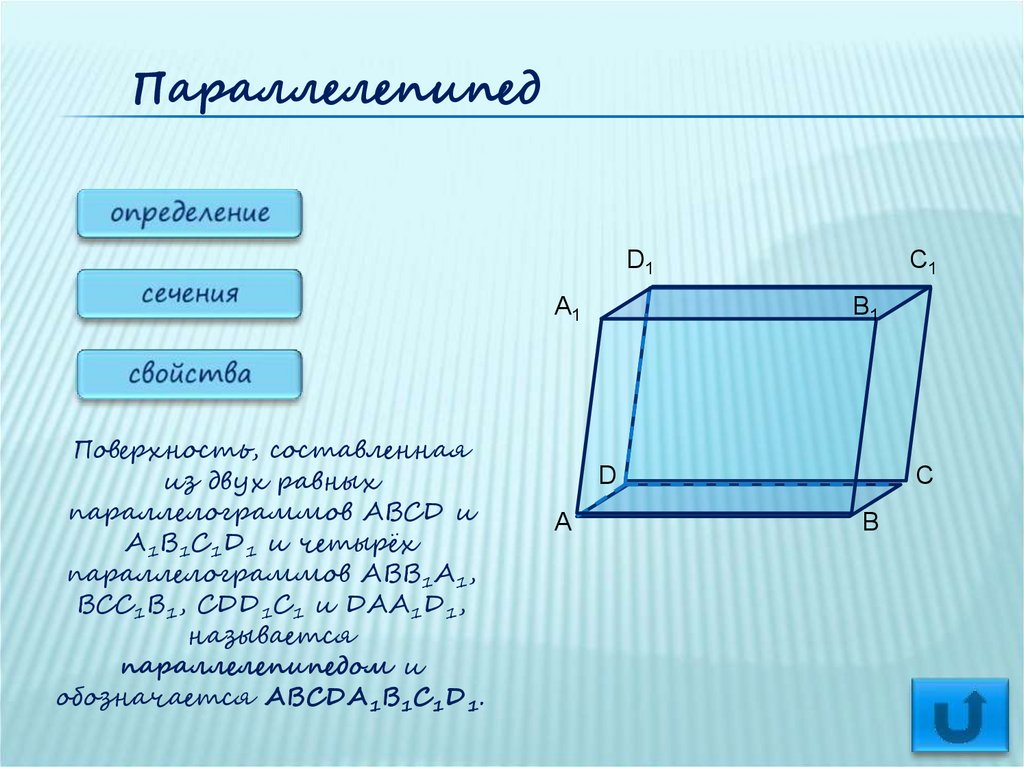
Поверхность, составленная
из двух равных
параллелограммов ABCD и
A1B1C1D1 и четырёх
параллелограммов ABB1A1,
BCC1B1, CDD1C1 и DAA1D1,
называется
параллелепипедом и
обозначается ABCDA1B1C1D1.
C1
B1
D
A
C
B

5.

Параллелепипед

6.

Тетраэдр
Многоугольник, сторонами
которого являются
отрезки, по которым
секущая плоскость
пересекает грани тетраэдра,
называется сечением
тетраэдра.

7.

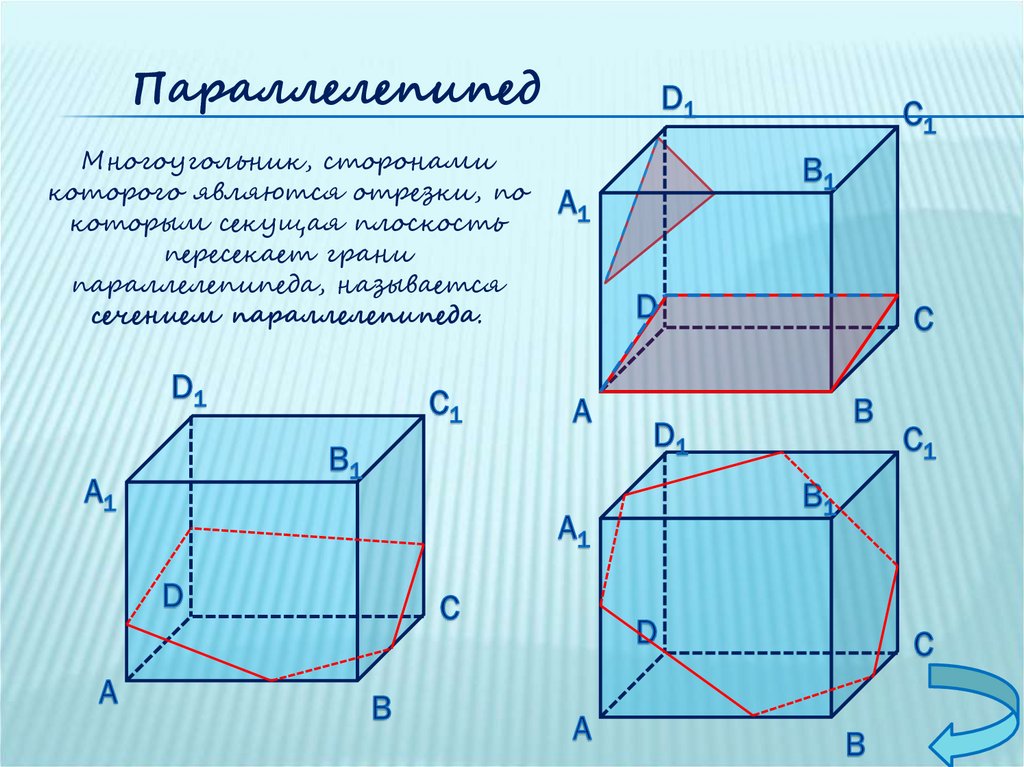
Параллелепипед
Многоугольник, сторонами
которого являются отрезки, по
которым секущая плоскость
пересекает грани
параллелепипеда, называется
сечением параллелепипеда.

8.

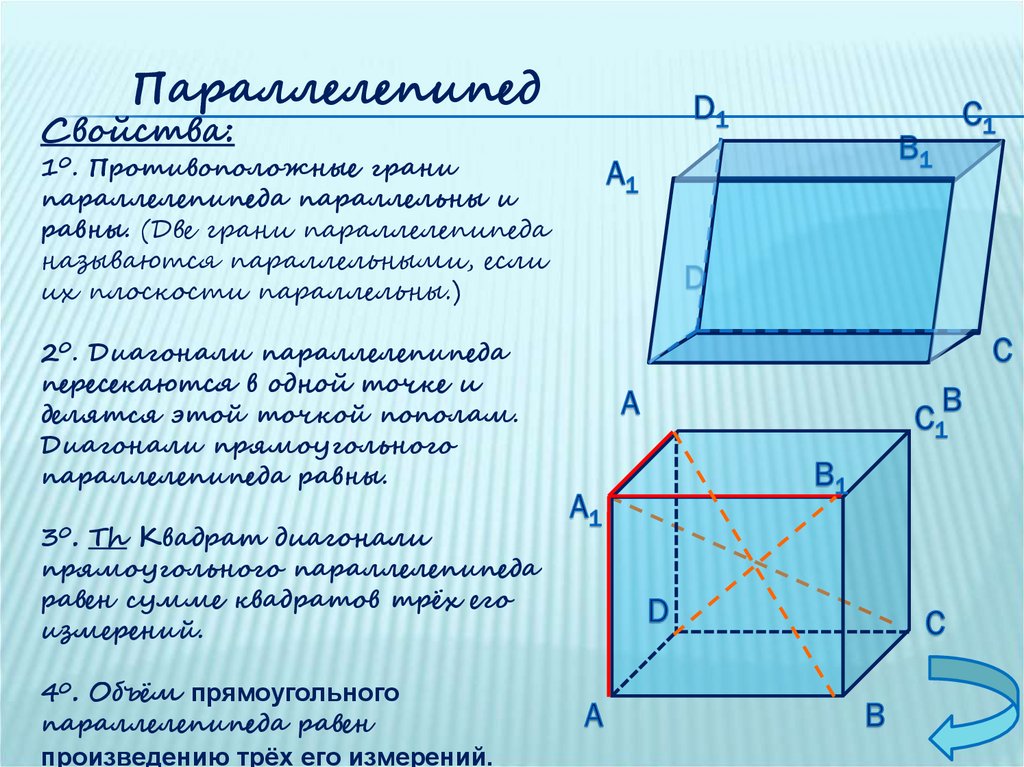
Параллелепипед
Свойства:
10. Противоположные грани
параллелепипеда параллельны и
равны. (Две грани параллелепипеда
называются параллельными, если
их плоскости параллельны.)
20. Диагонали параллелепипеда
пересекаются в одной точке и
делятся этой точкой пополам.
Диагонали прямоугольного
параллелепипеда равны.
30. Th Квадрат диагонали
прямоугольного параллелепипеда
равен сумме квадратов трёх его
измерений.
40. Объём прямоугольного
параллелепипеда равен
произведению трёх его измерений.

9.

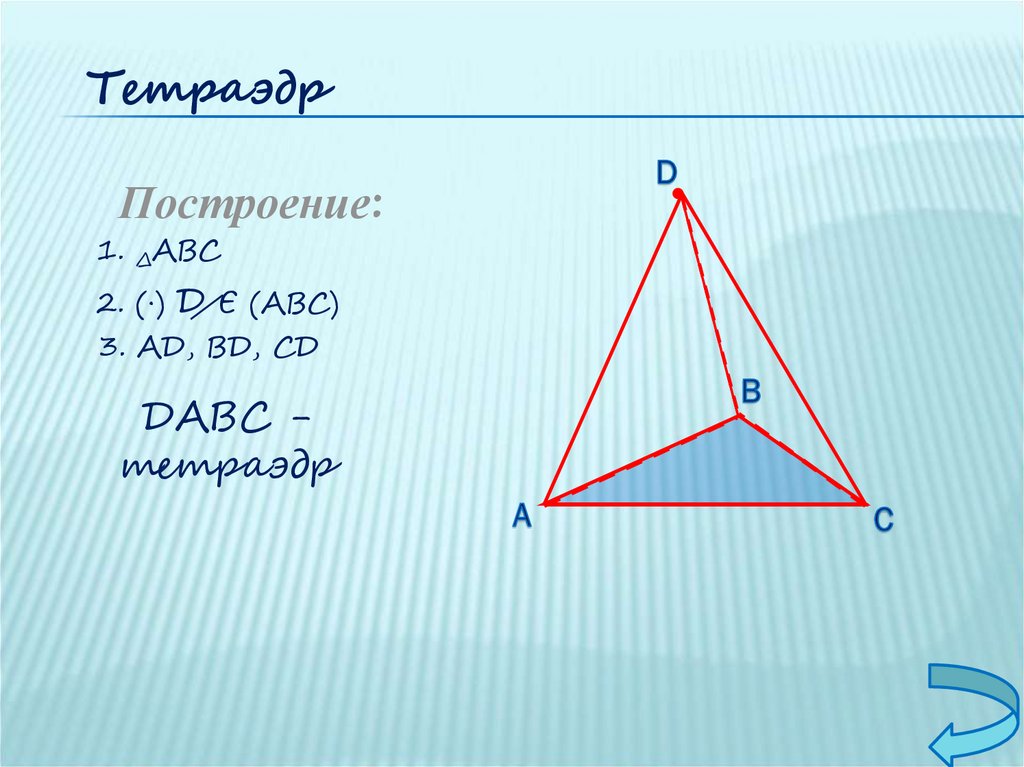
Тетраэдр
Построение:
1. ∆АВС
2. (∙) Д Є (АВС)
3. АД, ВД, СД
ДАВС тетраэдр