Тетраэдр и параллелепипед

1.

Геометрия 10 класс
Тема:
«Тетраэдр,
параллелепипед»

2.

Тетраэдр
Параллелепипед
Практика

3.

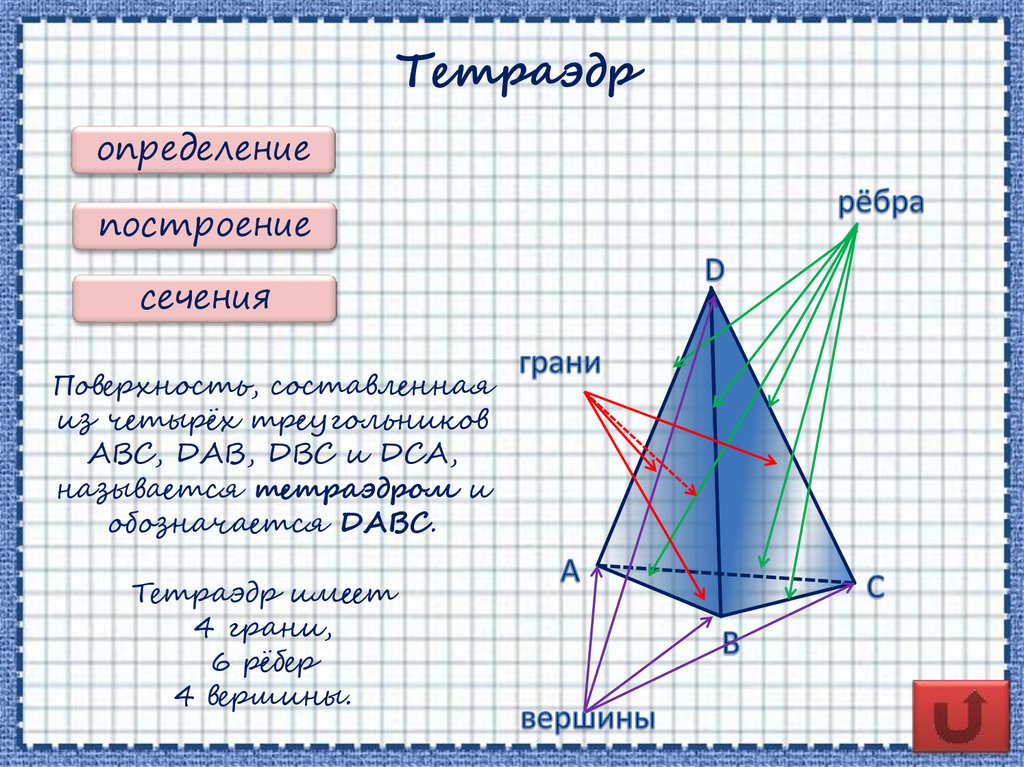
Тетраэдр
определение
построение
сечения
Поверхность, составленная
из четырёх треугольников
ABC, DAB, DBC и DCA,
называется тетраэдром и
обозначается DABC.
Тетраэдр имеет
4 грани,
6 рёбер
4 вершины.

4.

Параллелепипед
Далее
определение
сечения
свойства
Поверхность,
составленная из двух
равных
параллелограммов ABCD
и A1B1C1D1 и четырёх
параллелограммов
ABB1A1, BCC1B1, CDD1C1 и
DAA1D1, называется
параллелепипедом и
обозначается
ABCDA1B1C1D1.
D1
C1
A1
B1
D
A
C
B

5.

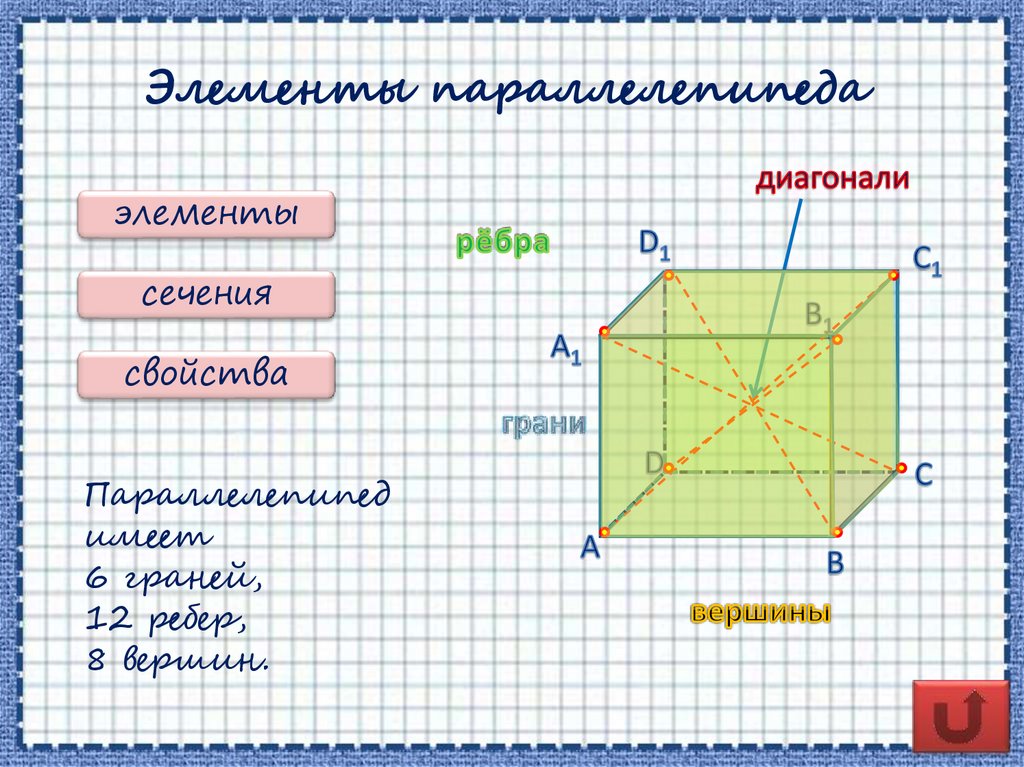
Элементы параллелепипеда
элементы
сечения
свойства
Параллелепипед
имеет
6 граней,
12 ребер,
8 вершин.

6.

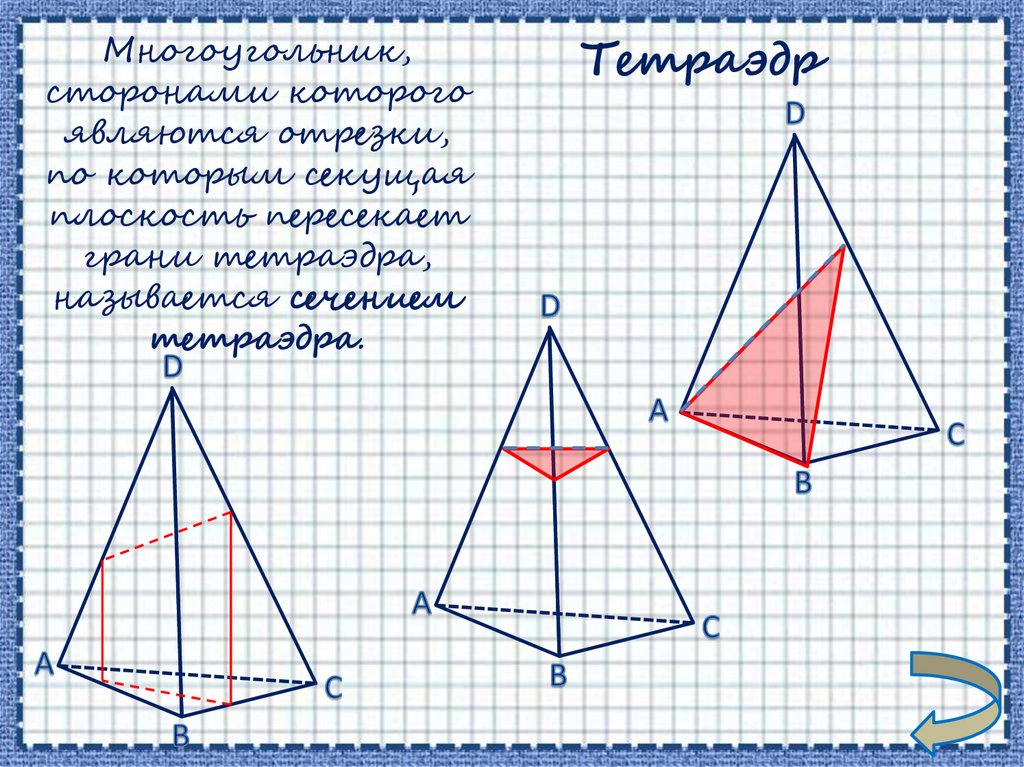
Многоугольник,
сторонами которого
являются отрезки,
по которым секущая
плоскость пересекает
грани тетраэдра,
называется сечением
тетраэдра.
Тетраэдр

7.

Параллелепипед
Многоугольник, сторонами
которого являются отрезки,
по которым секущая
плоскость пересекает грани
параллелепипеда, называется
сечением параллелепипеда.

8.

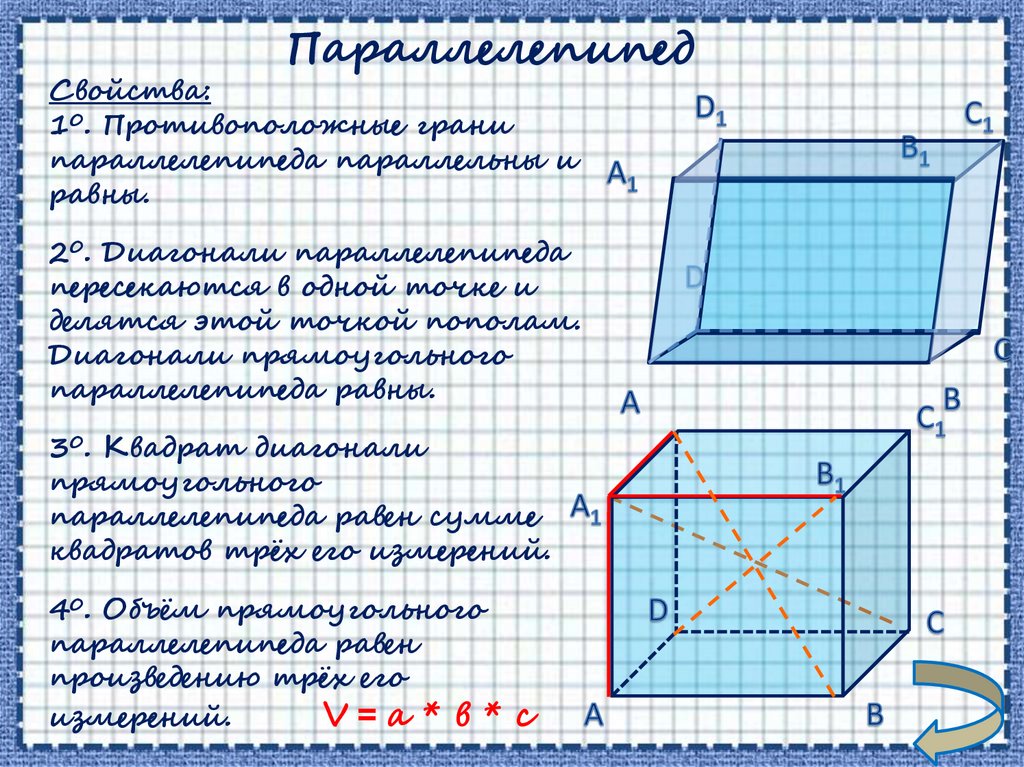
Параллелепипед
Свойства:
10. Противоположные грани
параллелепипеда параллельны и
равны.
20. Диагонали параллелепипеда
пересекаются в одной точке и
делятся этой точкой пополам.
Диагонали прямоугольного
параллелепипеда равны.
30. Квадрат диагонали
прямоугольного
параллелепипеда равен сумме
квадратов трёх его измерений.
40. Объём прямоугольного
параллелепипеда равен
произведению трёх его
измерений.
V=а * в * с

9.

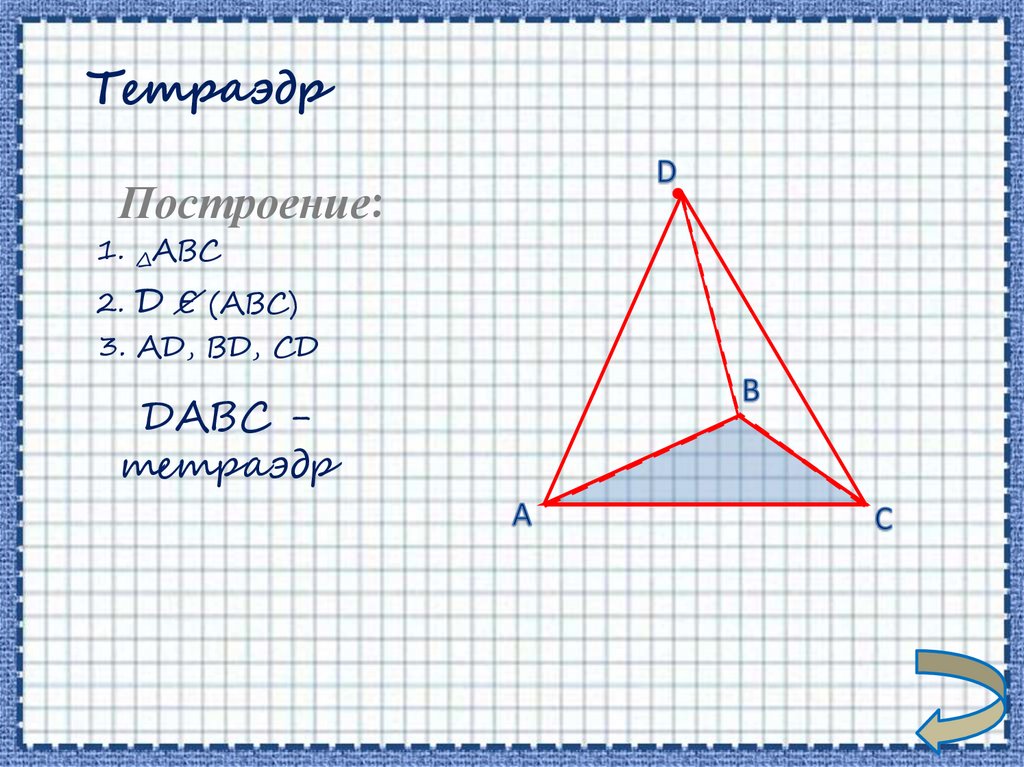
Тетраэдр
Построение:
1. ∆АВС
2. Д Є (АВС)
3. АД, ВД, СД
ДАВС тетраэдр

10.

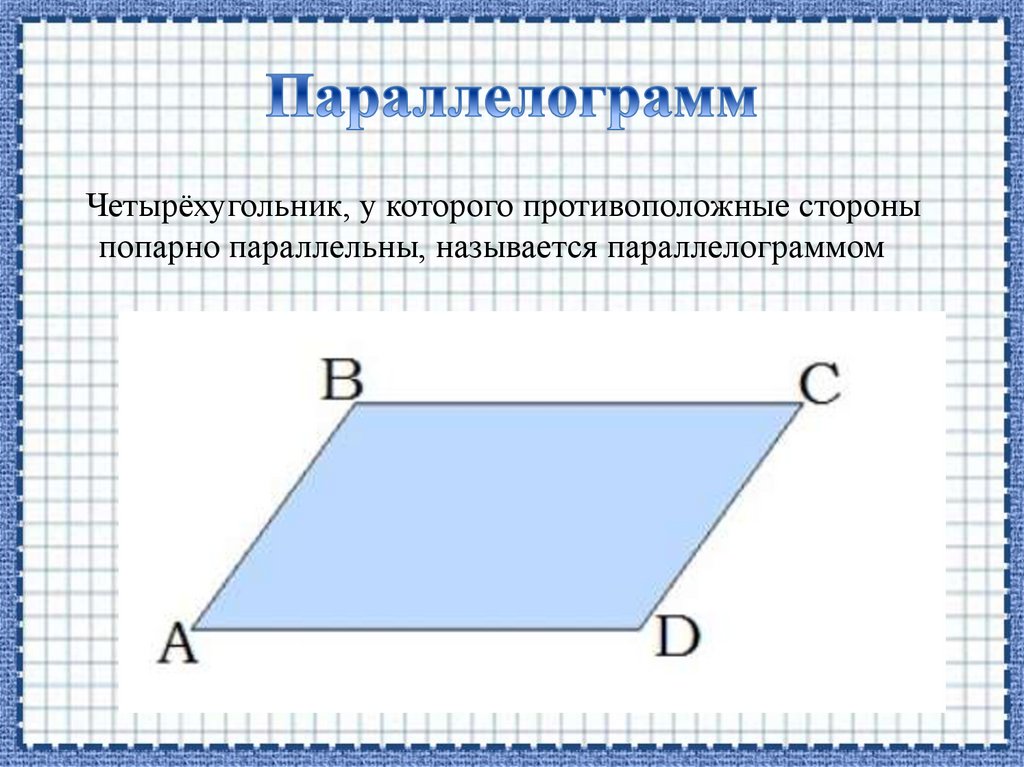
Четырёхугольник, у которого противоположные стороны
попарно параллельны, называется параллелограммом

11.

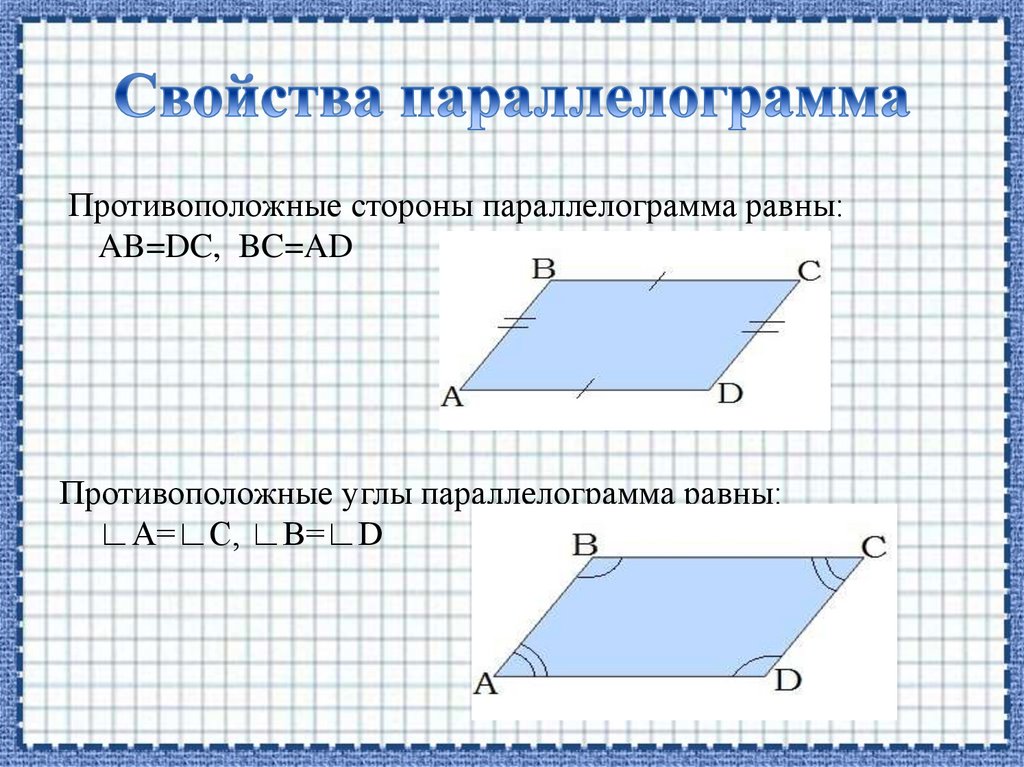
Противоположные стороны параллелограмма равны:
AB=DC, BC=AD
Противоположные углы параллелограмма равны:
∟A=∟C, ∟B=∟D

12.

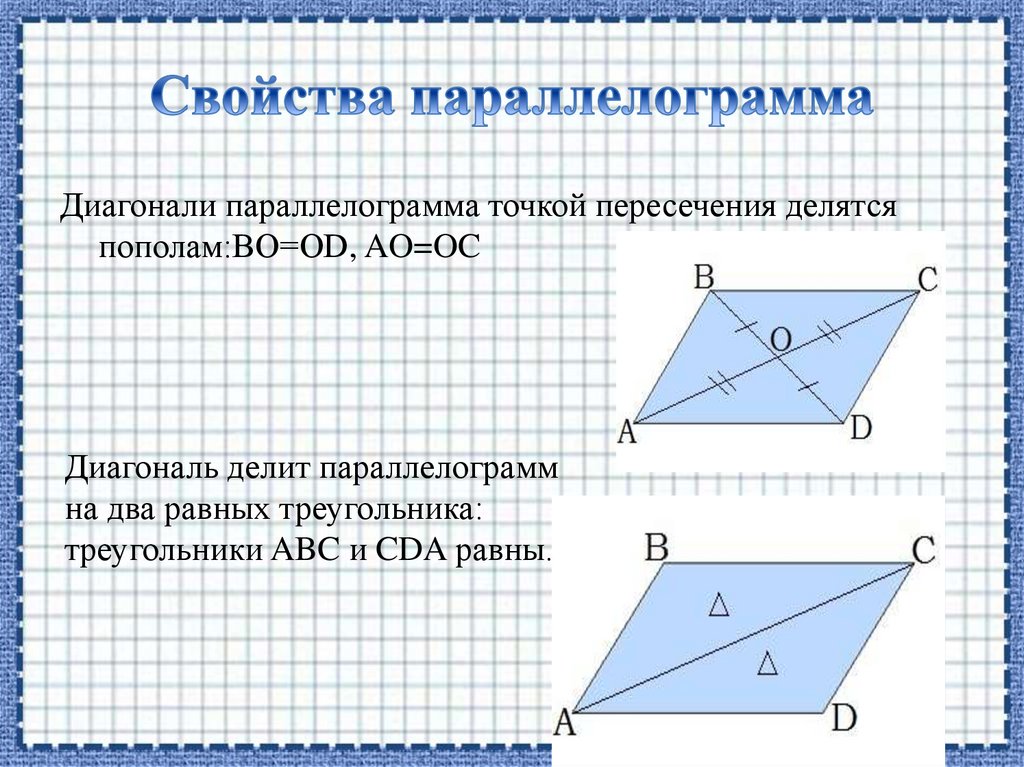
Диагонали параллелограмма точкой пересечения делятся
пополам:BO=OD, AO=OC
Диагональ делит параллелограмм
на два равных треугольника:
треугольники ABC и CDA равны.

13.

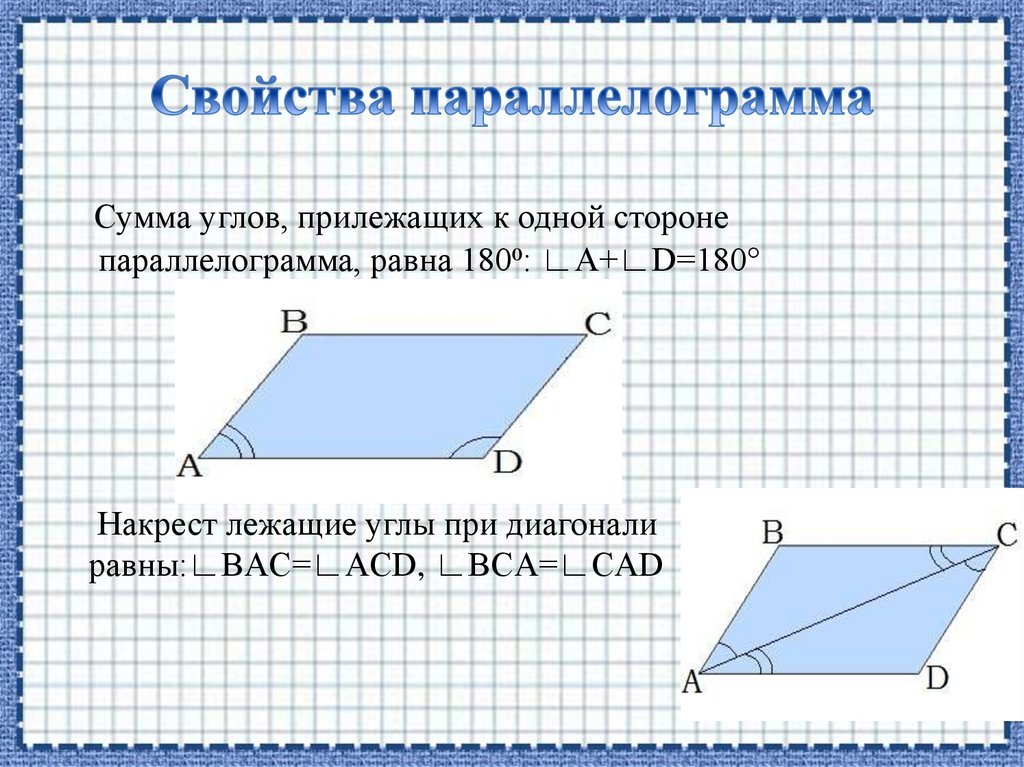
Сумма углов, прилежащих к одной стороне
параллелограмма, равна 180⁰: ∟A+∟D=180°
Накрест лежащие углы при диагонали
равны:∟BAC=∟ACD, ∟BCA=∟CAD