Похожие презентации:
Вычисление криволинейных интегралов. Лекция 12
1.
А.К.Рынская. Лекция №12III. Вычисление криволинейных
интегралов первого рода
1. Пусть кривая АВ - плоская и задается уравнением
y y x , x a; b , где y x - функция, непрерывно дифференцируемая на a; b , a точкам А и В соответствуют
значения x a и x b соответственно. Тогда
b
f x, y dl f x, y x 1 y x dx
AB
2
a
1 y x dx dl - дифференциал длины дуги кривой.
2
2.
2. Если кривая АВ - плоская и задается уравнениемx x y , y c; d , где x y - функция, непрерывно дифференцируемая на c; d , а точкам А и В соответствуют
значения y c и y d , то
d
f x, y dl f x y , y 1 x y dy
AB
2
c
dl 1 x y dy - дифференциал длины дуги кривой.
2
3.
3. Пусть кривая АВ - плоская и задается параметрическими уравнениямиx x t , y y t , t ,
где x t и y t - функции, непрерывно дифференцируемые
на , , a точкам А и В соответствуют значения параметра t и t . Тогда
f x, y dl f x t , y t x t y t dt.
2
AB
dl
2
x t y t dt - дифференциал длины дуги кривой
2
2
4.
Пусть АВ - пространственная кривая изадается параметрическими уравнениями
x x t , y y t , z z t , t ,
где x t , y t , z t - функции, непрерывно дифференцируемые на , , а точкам А и В
соответствуют значения параметра t
и
t . Тогда
4.
f x, y, z dl f x t , y t , z t x t y t z t dt.
2
2
AB
dl
2
x t y t z t dt
2
2
2
дифференциал длины дуги кривой.
5.
Примерыx
dl вдоль параболы y x 2 1 от точки
1. Вычислить
AB 4 y 5
A 0; 1 до точки B
2;1 .
b
f x, y dl f x, y x 1 y x dx
Р е ш е н и е.
AB
x
dl
AB 4 y 5
a
2
x
2
1 2 x dx
2
0 4 x 1 5
x 1 4x
dx
2
4x 1
0
0
2
2
2
1
2
2
1
2
4x 1
80
2
1
2
1
2
dx
1
2
4x 1
4 x2 1 2 0
1
2
4
x
1
d 4x 1
4
2
xdx
2
2
2
0
3 1 1
4 4 2
6.
x3
3
dl вдоль кривой AB: x cos t , y sin t , t ; .
2. Вычислить
4 2
AB y
3
Р е ш е н и е.
f x, y dl f x t , y t x t y t dt
2
2
AB
dl
3cos t ( sin t ) 3sin t cos t dt
2
2
2
2
9cos t sin t 9sin t cos tdt
4
2
4
2
3cos t sin t cos t sin tdt 3cos t sin tdt
2
2
7.
x3
3
dl вдоль кривой AB: x cos t, y sin t, t ; .
2. Вычислить
4 2
AB y
3
f x, y dl f x t , y t x t y t dt
2
2
AB
dl 3cos t sin tdt
3
2 cos t
2 cos2 t
x
dl 3 3cos t sin tdt 3
dt
2
sin t
AB y
sin t
4
2 1 sin 2 t
4
2
1
2
3
dt 3 2 dt 3 dt 3ctgt 3
2
sin t
4
sin t
2 4
4
3
3
4
2
4
4
8.
КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫВТОРОГО РОДА
I. Определение интеграла второго рода
Пусть в пространстве (или на плоскости) задана непрерывная кривая АВ, в точках которой определена функция P(M).
1. Разобьем кривую АВ на п дуг точками
M 0 , M1 ,..., M n , следующими друг за другом. При этом точку
M 0 отождествим с точкой А, а точку Мп - с точкой В. КоорM 0 , M1 , M 2 ,..., M n
динаты
точек
обозначим
через
x0 , y0 , z0 , x1 , y1 , z1 , x2 , y2 , z2 ,..., xn , yn , zn . Наибольшую
из длин дуг M i 1M i обозначим через .
9.
2. На каждой дуге M i 1M i выберем произвольно поточке Ni xi ; yi ; zi и вычислим P xi , yi , zi , i 1,2,..., n .
3. Обозначим через Δxi разность xi xi 1 и вычислим сумму
n
P xi , yi , zi Δxi
- интегральная сумма для функции
i 1
P( x, y, z ) на дуге АВ по переменной х.
n
4.
lim P xi ; yi ; zi Δxi
0 i 1
Если этот предел существует, конечен и не зависит от способа разбиения кривой АВ на части и
выбора точек Ni , то он называется криволинейным интегралом второго рода от функции
P ( x, y , z ) no кривой АВ от точки А до точки В по
переменной x.
10.
Обозначение:P( x, y, z )dx
AB
n
P xi , yi , zi Δxi
P( x, y, z )dx lim
0
AB
i 1
Аналогично определяются
n
P xi , yi , zi Δyi
P( x, y, z )dy lim
0
AB
i 1
n
P xi , yi , zi Δzi
P( x, y , z )dz lim
0
AB
i 1
11.
Если на кривой АВ определены три функции P ( x, y , z ) ,Q ( x, y , z ) , R ( x, y , z ) , то сумму интегралов
P ( x, y , z )dx Q ( x , y , z )dy R ( x , y , z )dz называют
AB
AB
AB
криволинейным интегралом (общего вида) второго рода по
кривой АВ в направлении от А к В.
Обозначение:
P( x, y, z )dx Q( x, y, z )dy R( x, y, z )dz
AB
12.
II. Основные свойства криволинейныхинтегралов второго рода
n
1. P( x, y, z )dx P( x, y , z )dx !
AB
P xi ; yi ; zi Δxi
P( x, y, z )dx lim
0
i 1
AB
BA
2. kP( x, y, z )dx k P( x, y, z )dx
AB
AB
3. P( x, y, z ) G ( x, y, z ) dx P( x, y, z )dx G ( x, y, z )dx
AB
AB
AB
4. Свойство аддитивности
Если кривая АВ разбита точкой С на две части АС и СВ, то
P( x, y, z )dx P( x, y, z )dx P( x, y, z )dx
AB
AC
CB
5. Если L - замкнутая кривая, то криволинейный интеграл
не зависит от выбора начальной точки, а зависит только от
направления движения вдоль кривой.
13.
III. Вычисление криволинейных интеграловвторого рода
1. Пусть АВ - плоская кривая и задается уравнением
y y x , точка А имеет координаты a; y a , точка
В - координаты b; y b . Тогда
b
P( x, y )dx Q ( x, y )dy P x, y x Q x, y x y x dx
AB
a
Если плоская кривая АВ задается уравнением
x x y , а точки А и B имеют координаты
x c , c и x d , d , то
d
P( x, y )dx Q ( x, y )dy P x y , y x y Q x y , y dy
AB
c
14.
2. Пусть АВ - плоская кривая, задаваемая па-раметрическими уравнениями: x x t , y y t ,
причем точке А соответствует значение параметра
t , точке В - значение t . Тогда
P( x, y )dx Q( x, y )dy
AB
P x t , y t x t Q x t , y t y t dt
15.
3. Если АВ - пространственная кривая, задаваемаяпараметрическими
уравнениями:
x x t , y y t , z z t и точкам А и В соответствуют значения t и t , то
P( x, y, z )dx Q( x, y, z )dy R( x, y, z )dz
AB
P x t , y t , z t x t Q x t , y t , z t y t
R x t , y t , z t z t dt
16.
Примеры1. Вычислить xydx ( x 2 1)dy вдоль кривой L: x 2 y 2 1 от
L
точки A 1;0 до точки B 2; 3 .
Р е ш е н и е.
b
P( x, y )dx Q ( x, y )dy P x, y x Q x, y x y x dx
AB
a
x y 1 y x 1 y
2
2
2
x
x 1
2
2
2
(
x
1) x
2
2
2
dx
2
x
x
1dx
xydx ( x 1)dy x x 1 2
L
1
x 1
1
2
2
1
x 1d x 1
2
2
2 x2 1
3
2
2
2 3
3
1
17.
2. Вычислить ( x y )dx xdy вдоль дуги эллипса:L
x 2cos t, y sin t от точки A 0;1 до точки B 2;0 .
Р е ш е н и е.
P ( x, y )dx Q ( x, y )dy
AB
P x t , y t x t Q x t , y t y t
dl
, 0
2
0
( x y )dx xdy 2cos t sin t 2sin t 2cos t cos t dt
L
0
2
0
4cos t sin t 2sin 2 t 2cos2 t dt 2sin 2t 2 dt
2
2
18.
00
0
2sin 2t 2 dt 2 sin 2tdt 2 dt
0
2
2
2
sin 2td 2t 2t cos 2t 2t 1
0
0
2
2
2
19.
Связь между криволинейными интеграламипервого и второго рода
AB – кривая, на которой задано направление от точки A, к
точке B.
Рассмотрим в каждой точке кривой
B
касательный вектор, направление которого
соответствует направлению кривой.
, , углы, которые образует этот вектор
A
с осями Ox, Oy, Oz.
P( x, y, z )dx Q( x, y, z )dy R( x, y, z )dz
AB
P( x, y, z )cos Q( x, y, z )cos R( x, y, z )cos dl
AB
20.
Формула ГринаИнтегралы по замкнутому контуру
L
L – замкнутая плоская кривая(замкнутый
контур)
– криволинейный интеграл по
замкнутому контуру
L
Направление обхода контура называется положительным,
если область, которую ограничивает контур остается
слева.
Противоположное направление обхода называется
отрицательным.
21.
Связь двойного интеграла с криволинейнымТеорема.(Грина)
Q P
Пусть функции P( x, y ), Q ( x, y ),
,
непрерывны
x y
в области D, имеющей кусочно-гладкую границу.
Q P
dxdy P( x, y )dx Q ( x, y )dy
y
D x
L
L- граница области D, криволинейный интеграл берется в
положительном направлении
22.
Q Pdxdy P( x, y )dx Q ( x, y )dy
y
D x
L
Доказательство.
AnB : y ( x), AmB : y ( x)
y ( x)
y
m
L AnB BmA
B
A
n
y ( x)
a
b
f ( x )dx
f ( x)
x
Q P
Q
P
dxdy dxdy dxdy
y
D x
D x
D y
( x)
b
b
P
P
( x)
Рассмотрим
dxdy dx
dy dx P( x, y ) ( x )
D y
a
( x ) y
a
b
P( x, ( x )) P( x, ( x ))b dx
b
a
P( x, ( x ))dx P( x, ( x )dx
a
a
23.
Q Pdxdy P( x, y )dx Q ( x, y )dy
y
D x
L
y ( x)
y
Q P
Q
P
m
dxdy
dxdy
dxdy
B
D
A
b
b
a
b
x
( x)
dx P( x, y ) ( x )
b
y
D
x
D
y
( x)
b
P
P
dxdy dx y dy
a
( x)
D y
n
y ( x)
a
x
b
P( x, ( x)) P( x, ( x)) dx
a
P( x, ( x )dx P( x, ( x)dx P( x, y )dx P ( x, y )dx
a
AmB
a
AnB
P( x, y )dx P ( x, y )dx P ( x, y )dx
BmA
AnB
L
Q
dxdy Q ( x, y )dy
Аналогично
D x
L
24.
Q Pdxdy P( x, y )dx Q ( x, y )dy
y
D x
L
y ( x)
y
m
B
A
n
y ( x)
a
Q P
Q
P
dxdy
dxdy
dxdy
y
D x
D x
D y
P
dxdy P ( x, y )dx
b x D y
L
Q
dxdy Q ( x, y )dy
D x
L
Q P
dxdy P ( x, y )dx Q ( x, y )dy
y
L
D x
25.
Q Pdxdy P( x, y )dx Q ( x, y )dy
y
D x
L
3
П р и м е р. Вычислить x 3 y dx (5 x 1)dy , где L – контур
L
треугольника с вершинами в точках A 0;0 , B 2;0 , C 1;1 .
Направление обхода – положительное.
Р е ш е н и е.
P x 3 y,
3
y
C
1
A
B
2x
Q
5
x
Q 5x 1
P
,
3
y
3
x
3 y dx (5x 1)dy 5 3 dxdy 8 dxdy
L
D
1
8S 8 AB h 4 2 1 8
2
D

















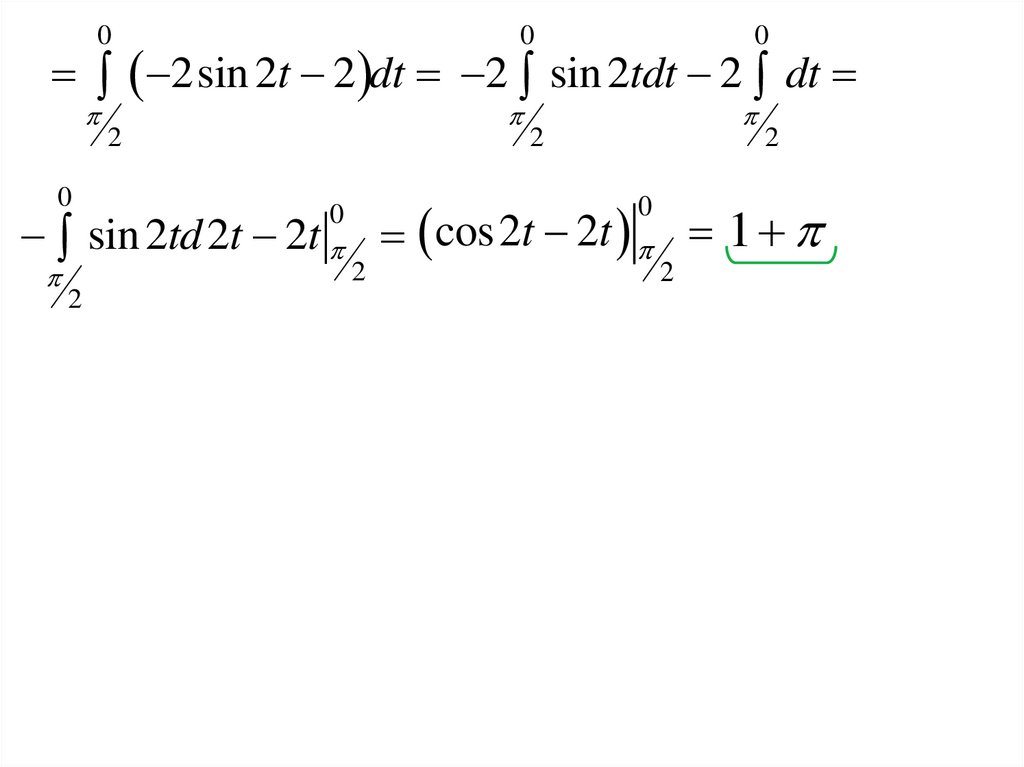





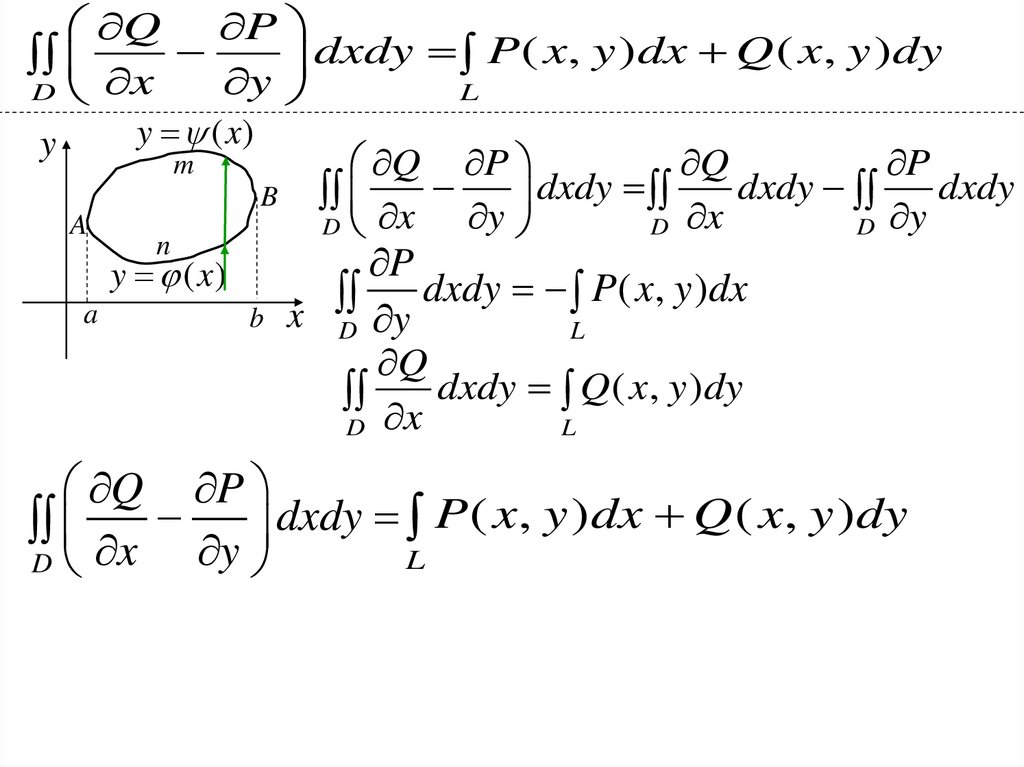

 Математика
Математика








