Похожие презентации:
Поворот точки вокруг начала координат. Урок №2
1.
Урок №2Поворот точки вокруг начала
координат
2.
Проверочная работаВариант 1
1800 = π
Вариант 2
3.
Ответы на проверочную работуОценка за проверочную работу:
7-8 верных ответов - оценка «3»
9-10 верных ответов – оценка «4»
11-12 верных ответов – оценка «5»
4.
Единичная окружностьОкружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
+α
1
М
точка Р - начало
отсчета углов
Р
α
О
-1
-α
1
-α
-1
5.
Единичная окружностьОкружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
α = 900
+α
точка Р - начало
отсчета углов
α = 1800
α = 00
О
Р α = 3600
-α
α = 2700
6.
Единичная окружностьОкружность с центром в начале координат и радиусом
равным 1 - называется единичной окружностью.
α = -2700
точка Р - начало
отсчета углов
α = -1800
α = 3600
О
Р α = 00
-α
α = -900
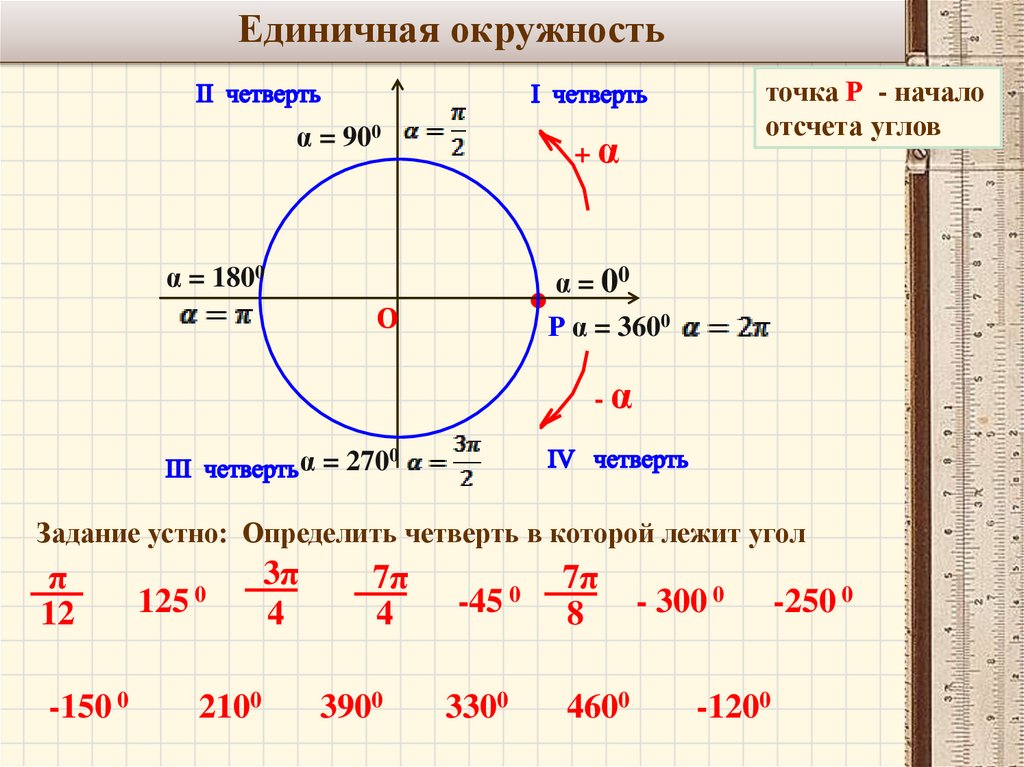
7.
Единичная окружностьα = 900
точка Р - начало
отсчета углов
+α
α = 1800
α = 00
О
Р α = 3600
-α
α = 2700
Задание устно: Определить четверть в которой лежит угол
π
12
-150 0
125 0
2100
3π
4
7π
4
3900
-45 0
7π
8
3300
4600
- 300 0
-1200
-250 0
8.
Координаты точки на единичной окружностиА (0;1)
900 =
Р (1;0)
В (-1;0)
00
О
1800 =
2700 =
3600=
С (0;-1)
Точке А (0,1)
соответствую углы:
900
900+3600
900+3600 +3600 +…
900-3600
900-3600 -3600 -…
Или в радианах:
9.
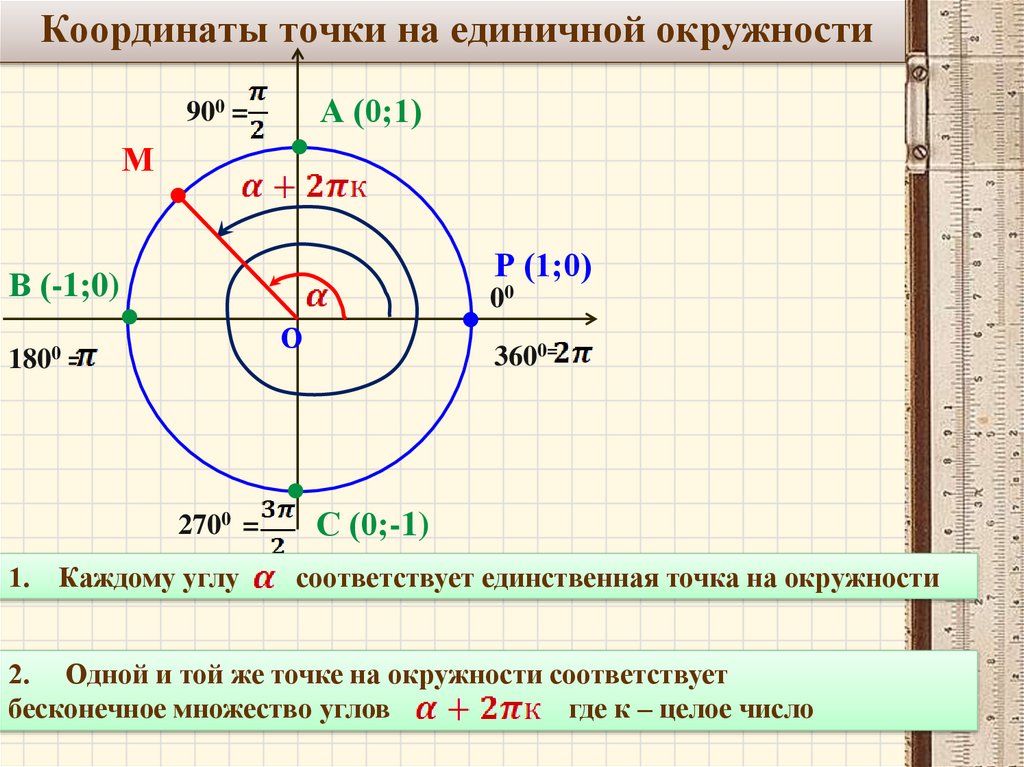
Координаты точки на единичной окружностиА (0;1)
900 =
М
Р (1;0)
В (-1;0)
00
О
1800 =
2700 =
1. Каждому углу
3600=
С (0;-1)
соответствует единственная точка на окружности
2. Одной и той же точке на окружности соответствует
бесконечное множество углов
где к – целое число
10.
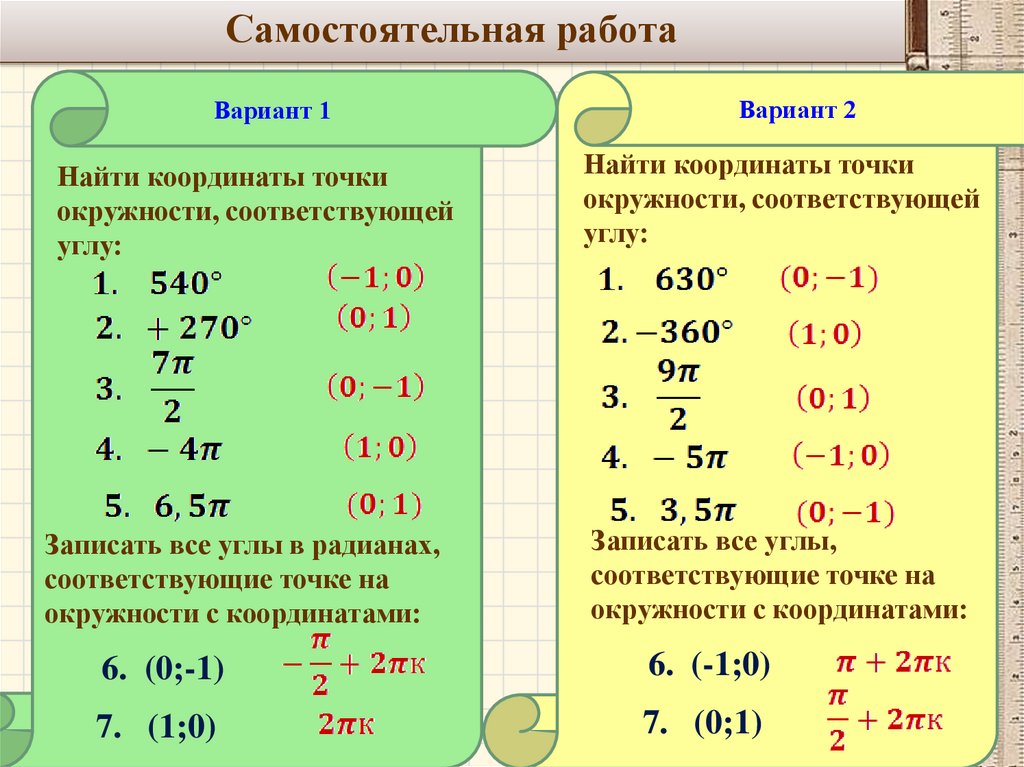
Самостоятельная работаВариант 1
Вариант 2
Найти координаты точки
окружности, соответствующей
углу:
Найти координаты точки
окружности, соответствующей
углу:
Записать все углы в радианах,
соответствующие точке на
окружности с координатами:
Записать все углы,
соответствующие точке на
окружности с координатами:
6. (0;-1)
6. (-1;0)
7. (1;0)
7. (0;1)








 Математика
Математика








