Теорема синусов Теорема косинусов

1. Определить вид треугольника (остроугольный, прямоугольный, тупоугольный)

• Стороны треугольника равны 3,4,5 см
• Стороны треугольника равны 5, 12,13 см
• Стороны треугольника равны 4, 6, 8 см
4 см
350
450
Найти стороны
треугольника

2. Теорема синусов Теорема косинусов

3. Цели урока

• Найти способ находить стороны и углы
треугольников по трем известным
элементам
• Доказать теорему синусов
• Доказать теорему косинусов

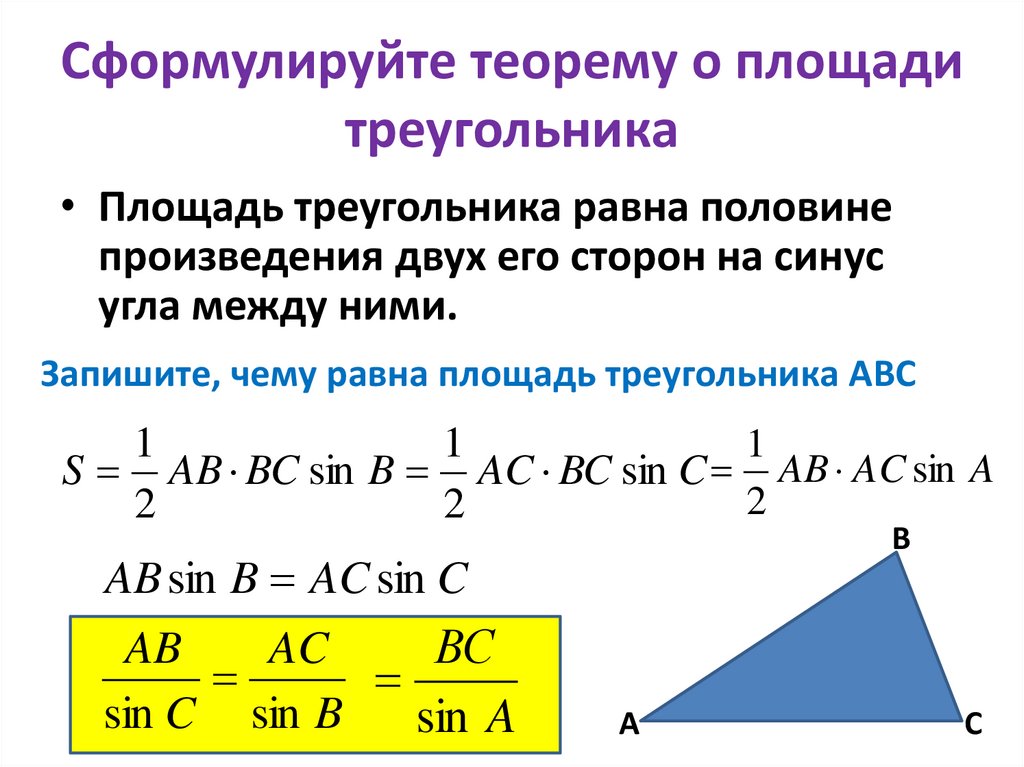
4. Сформулируйте теорему о площади треугольника

• Площадь треугольника равна половине
произведения двух его сторон на синус
угла между ними.
Запишите, чему равна площадь треугольника АВС
1
1
1
S AB BC sin B AC BC sin C AB AC sin A
2
2
2
AB sin B AC sin C
AB
AC
ВС
sin C sin B
sin A
В
А
С

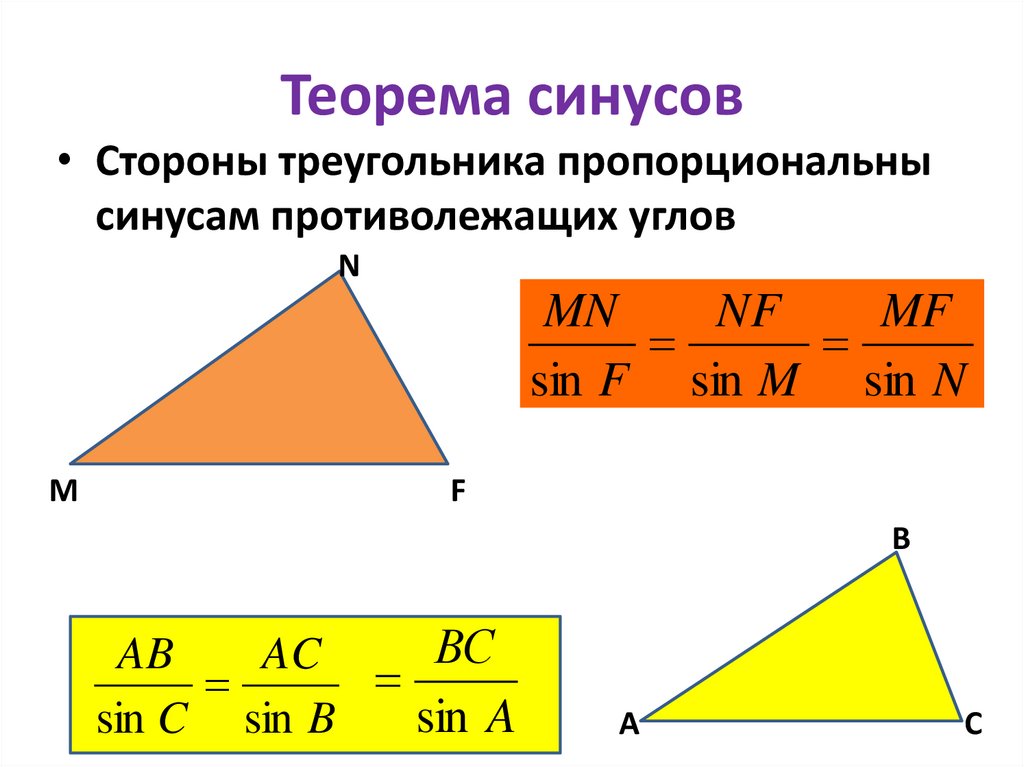
5. Теорема синусов

• Стороны треугольника пропорциональны
синусам противолежащих углов
N
MN
NF
MF
sin F sin M sin N
M
F
В
ВС
AB
AC
sin A
sin C sin B
А
С

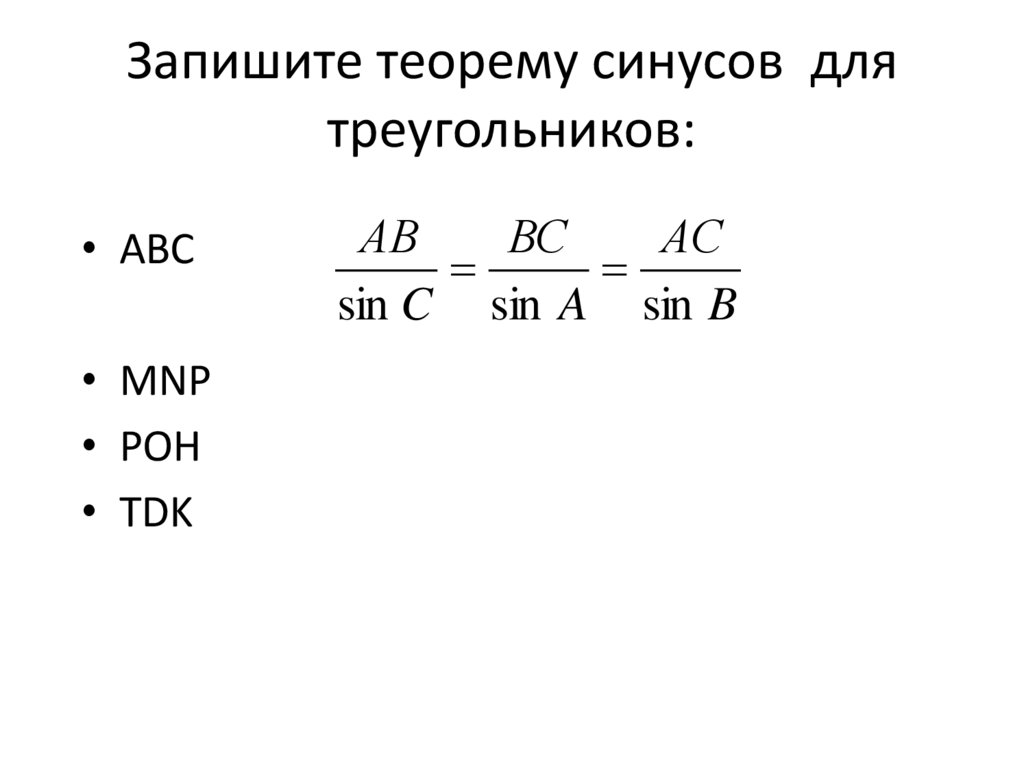
6. Запишите теорему синусов для треугольников:

• АВС
• МNP
• POH
• TDK
АВ
ВС
АС
sin C sin A sin B

7. Теорема косинусов

• Квадрат стороны треугольника равен сумме
квадратов двух других сторон минус
удвоенное произведение этих сторон на
косинус угла между ними.
N
F
M
MN MF FN 2MF FN cos F
2
2
2

8. Запишите теорему косинусов для треугольников:

• АВС
АВ AC BC 2 AC BC cos C
2
2
2
AC AB BC 2 AB BC cos B
2
2
2
BC AB AC 2 AB AC cos A
2
• MNP
• POH
• TDK
2
2

9. Доказательство:

у
С (bcos A;bsin A)
b
a
Дано:
ΔАВС
АВ=с
АС=b
BC=a
Доказать:
а 2 b 2 c 2 2bc cos A
А(0;0)
c
В (с;0) х
BC a b cos A c b 2 sin 2 A
2
2
2
b 2 cos 2 A b 2 sin 2 A 2bc cos A c 2
b 2 cos 2 A sin 2 A 2bc cos A c 2
b c 2bc cos A
2
2

10. Выразим косинус угла из теоремы косинусов

АВ AC BC 2 AC BC cos C
2
2
2
2 АС ВС cos C AC BC AB
2
2
AC BC AC
cos C
2 AC BC
2
2
2
2

11. Домашнее задание:

• П.97-98
• П.99 (решение задач – посмотреть)
• Задача