Начертательная геометрия. Лекция 2. Проекции прямой

1.

2.

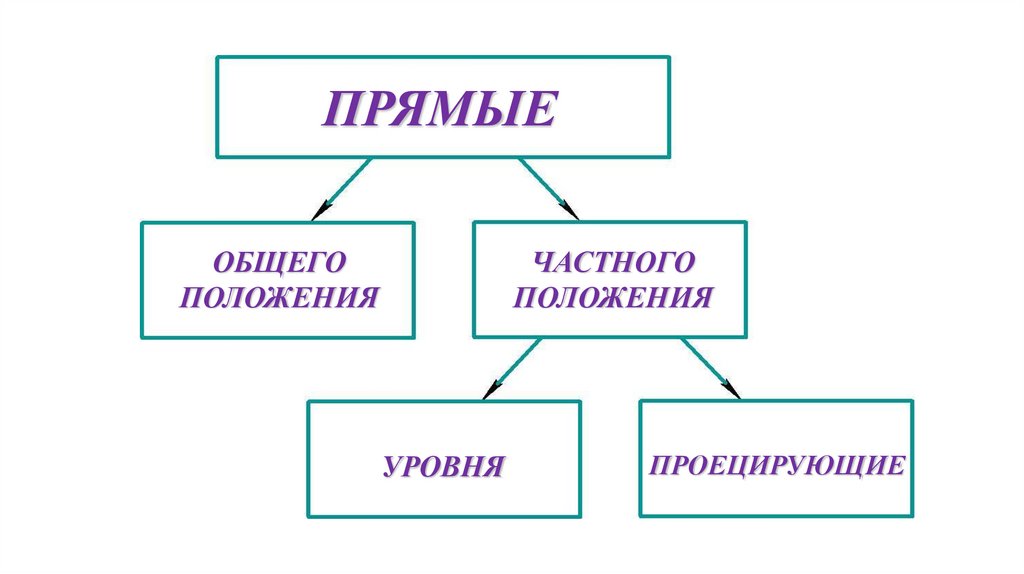
Проекции прямой

3.

ПРЯМЫЕ
ОБЩЕГО
ПОЛОЖЕНИЯ
ЧАСТНОГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ

4.

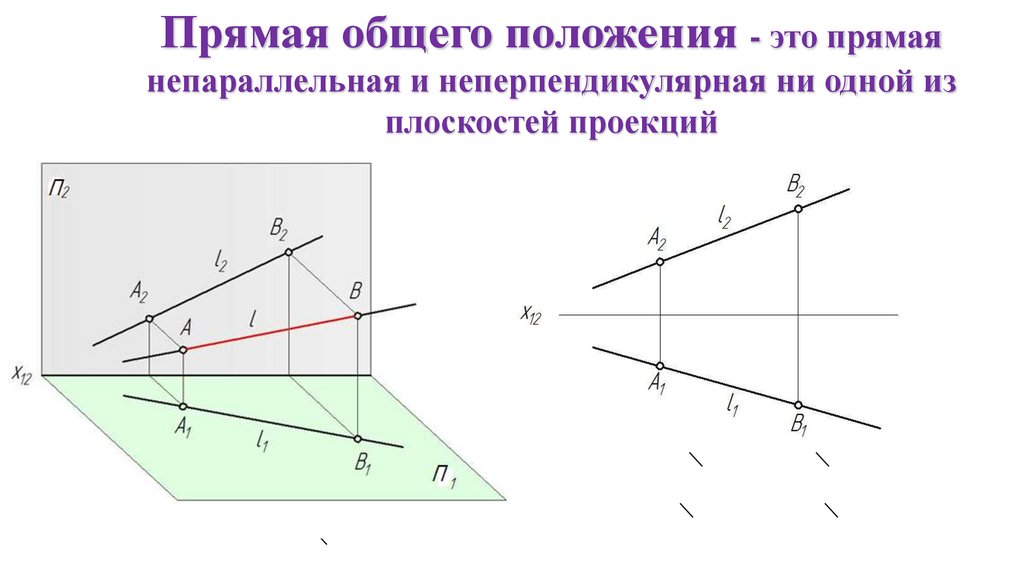
Прямая общего положения - это прямая
непараллельная и неперпендикулярная ни одной из
плоскостей проекций

5.

Прямые частного положения
Это прямые параллельные или перпендикулярные
плоскостям проекций
l II Пn или l Пn

6.

Прямая уровня
Это прямая параллельная одной из плоскостей
проекций
l II Пn

7.

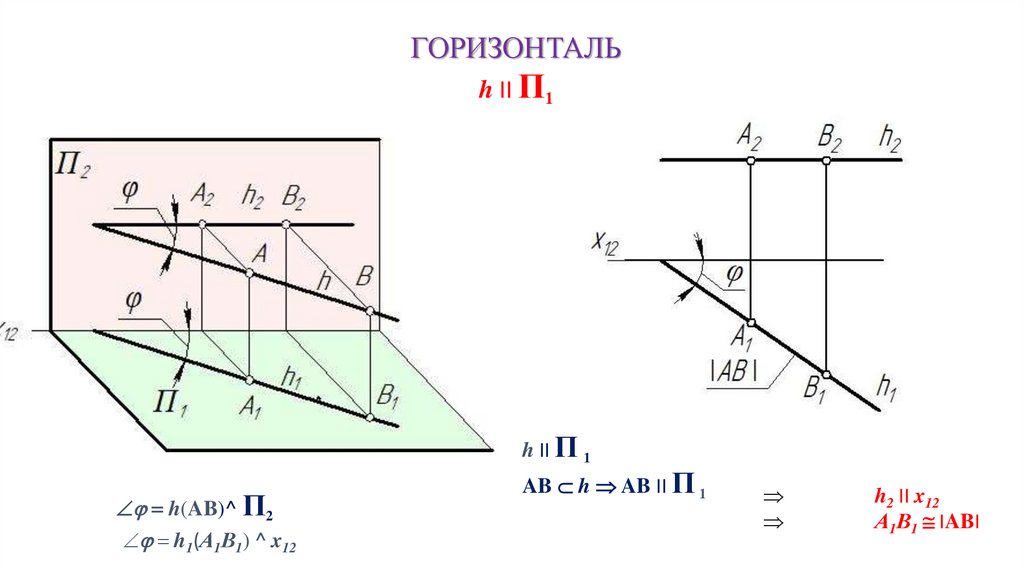
ГОРИЗОНТАЛЬ
h II П1
h II П 1
h(AB)^ П2
h1(А1В1) ^ x12
AB h AB II П 1
h2 II x12
А1В1 IABI

8.

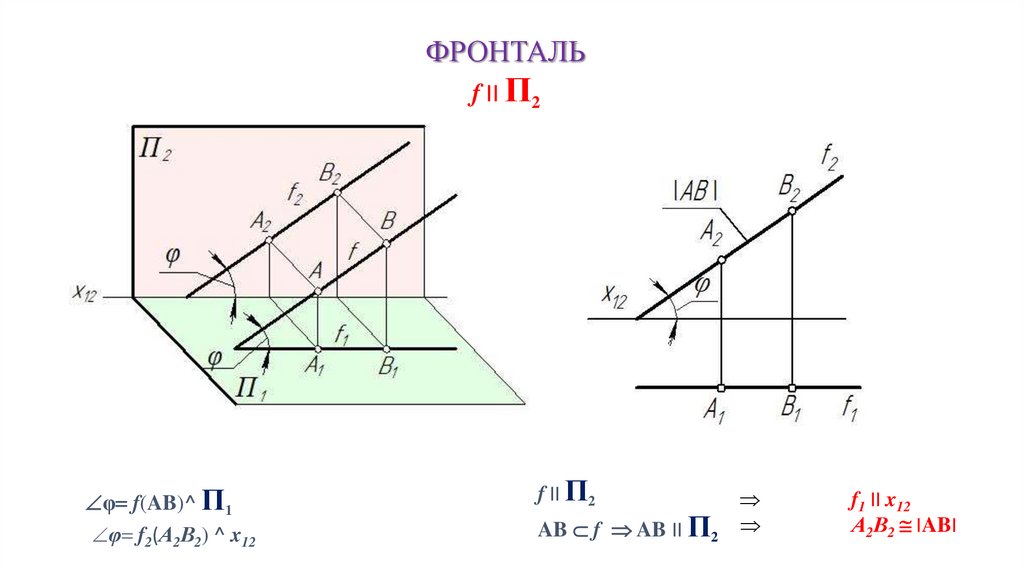
ФРОНТАЛЬ
f II П2
φ f(AB)^ П1
φ f2(А2В2) ^ x12
f II П2
AB f AB II П2
f1 II x12
А2В2 IABI

9.

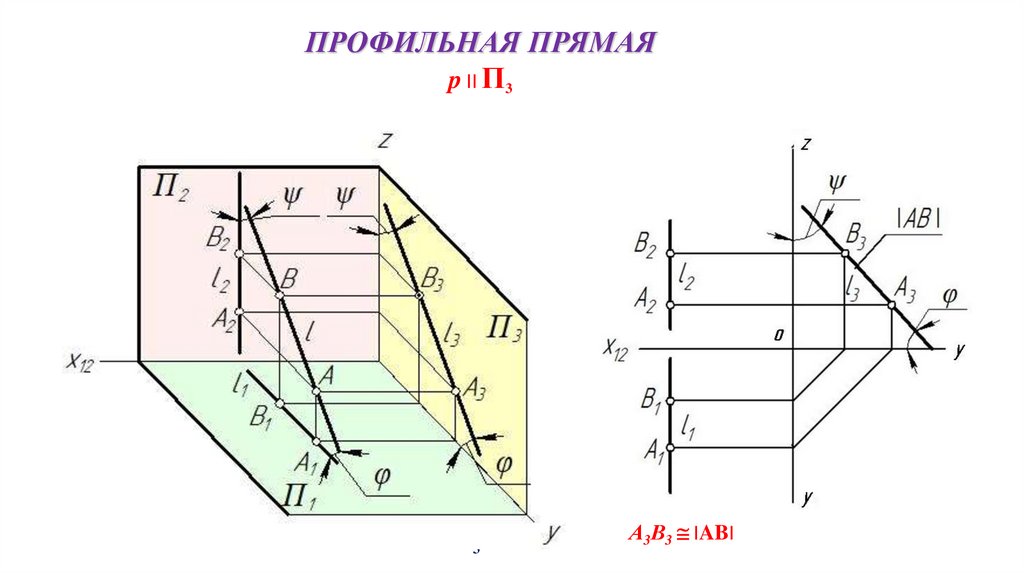
ПРОФИЛЬНАЯ ПРЯМАЯ
p II П3
l II П3
AB l AB II П3
А3В3 IABI

10.

Проецирующая прямая
Это прямая перпендикулярная одной из
плоскостей проекций
l П n

11.

ГОРИЗОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
m П1

12.

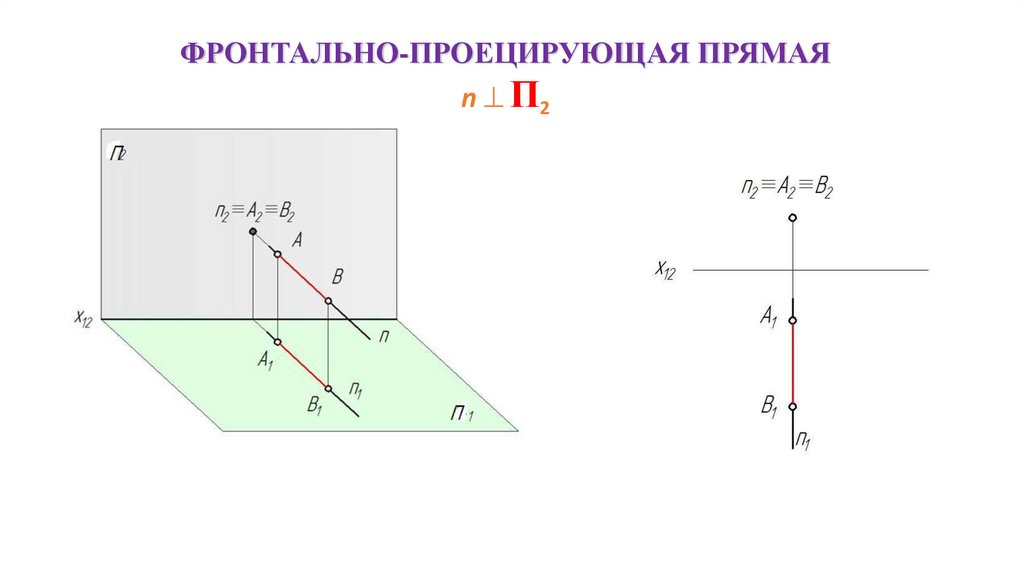
ФРОНТАЛЬНО-ПРОЕЦИРУЮЩАЯ ПРЯМАЯ
n П2

13.

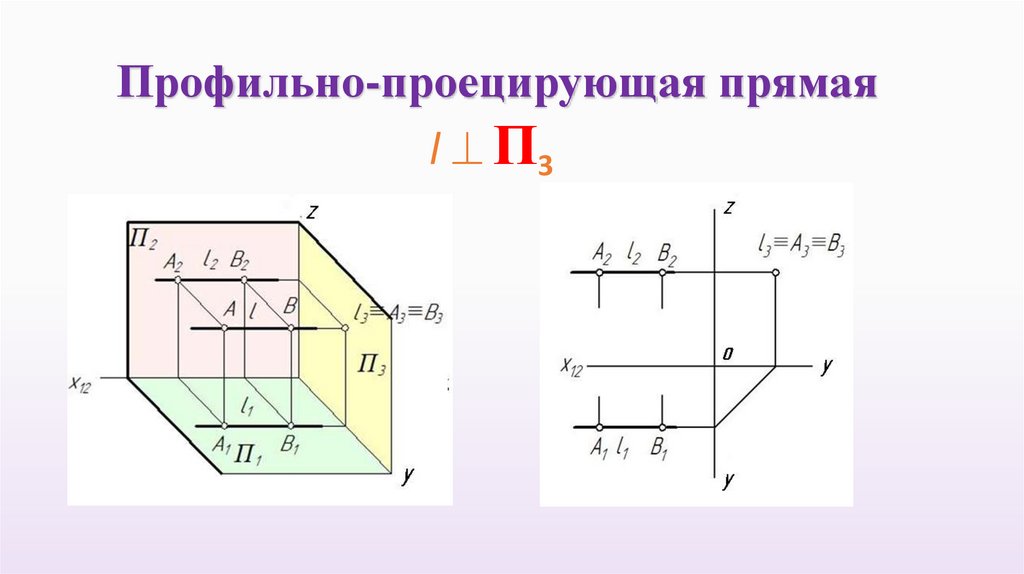
Профильно-проецирующая прямая
l П3

14.

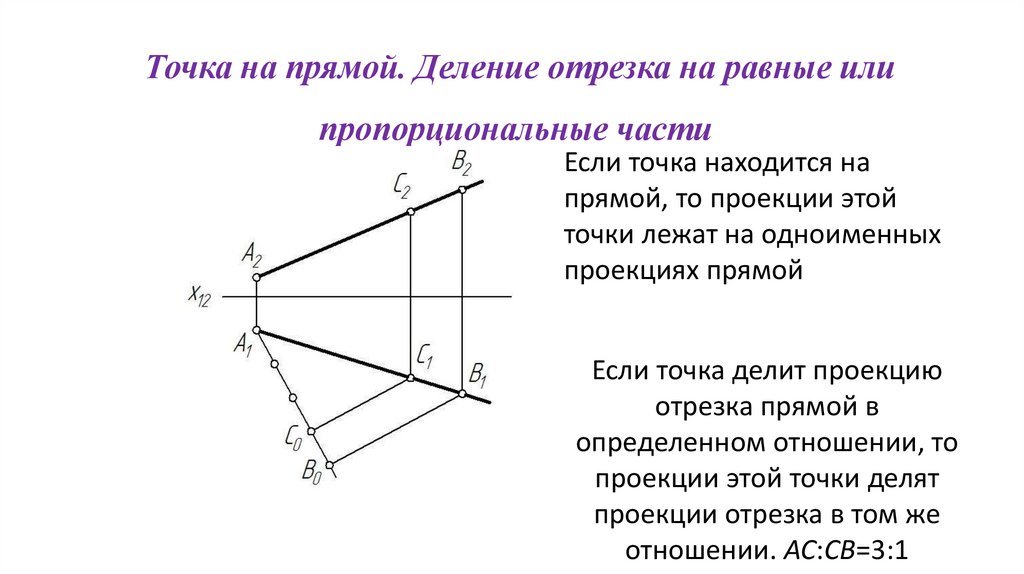
Точка на прямой. Деление отрезка на равные или
пропорциональные части
Если точка находится на
прямой, то проекции этой
точки лежат на одноименных
проекциях прямой
Если точка делит проекцию
отрезка прямой в
определенном отношении, то
проекции этой точки делят
проекции отрезка в том же
отношении. АС:СВ=3:1

15.

Взаимное положение двух
прямых

16.

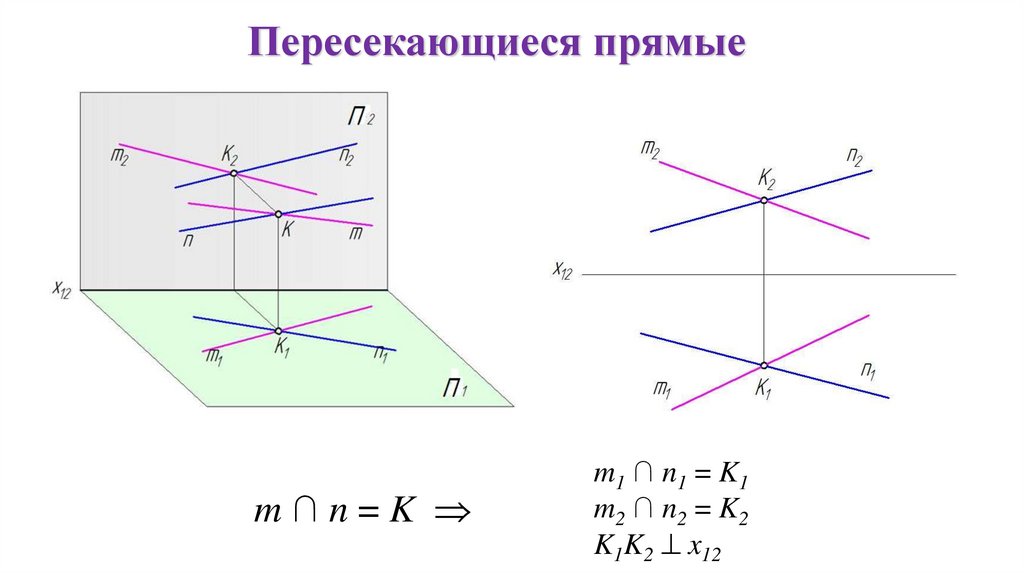
Пересекающиеся прямые
m∩n=K
m1 ∩ n1 = K1
m2 ∩ n2 = K2
K1K2 x12

17.

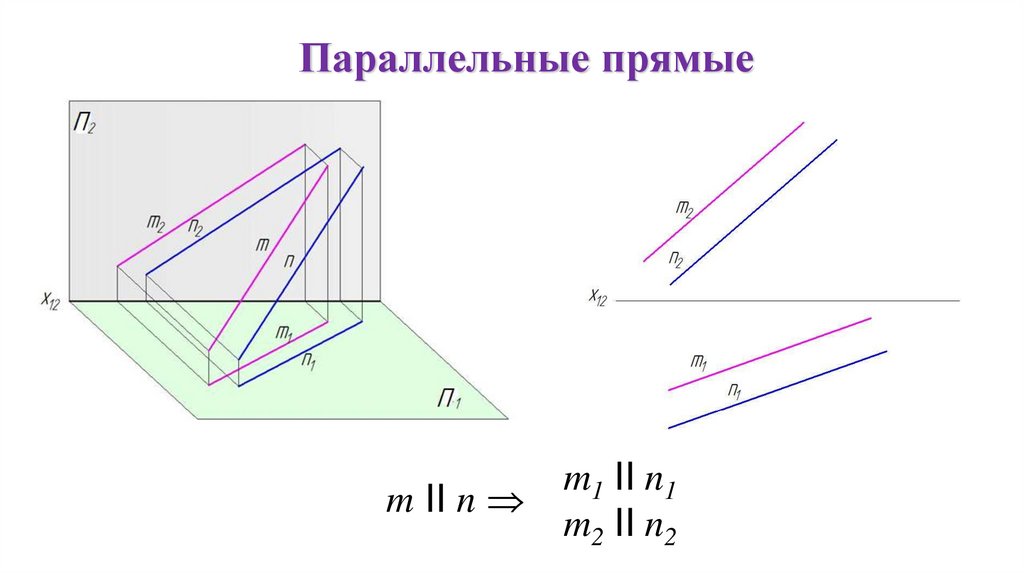
Параллельные прямые
m II n
m1 II n1
m2 II n2

18.

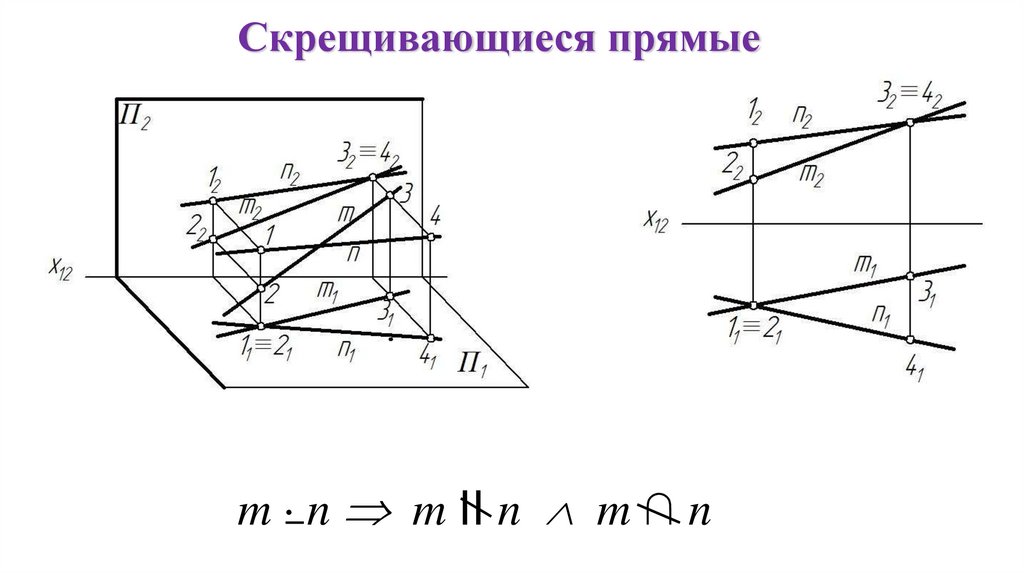
Скрещивающиеся прямые
m n m II n m ∩ n

19.

Проекции
плоскости

20.

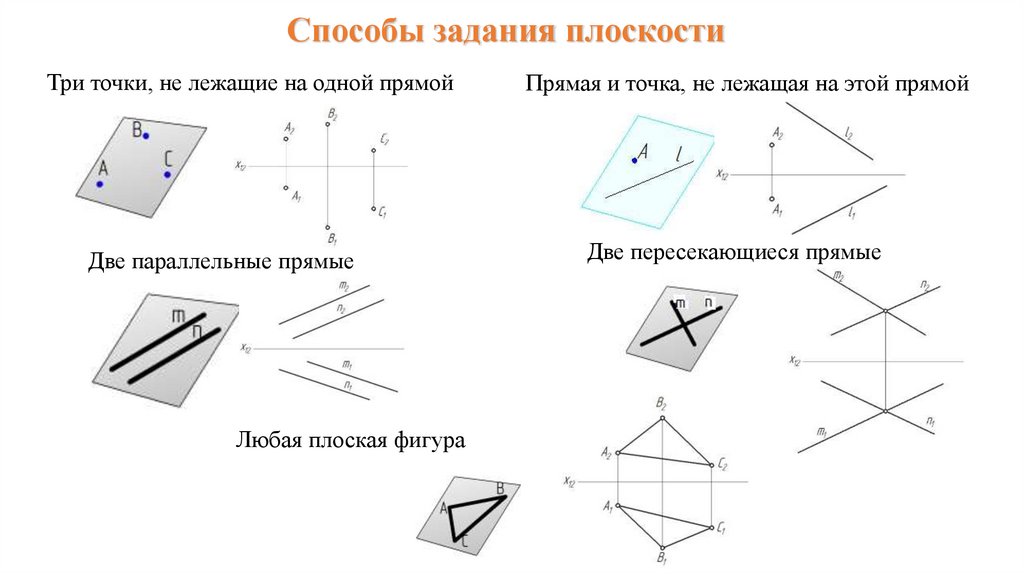
Способы задания плоскости
Три точки, не лежащие на одной прямой
Две параллельные прямые
Любая плоская фигура
Прямая и точка, не лежащая на этой прямой
Две пересекающиеся прямые

21.

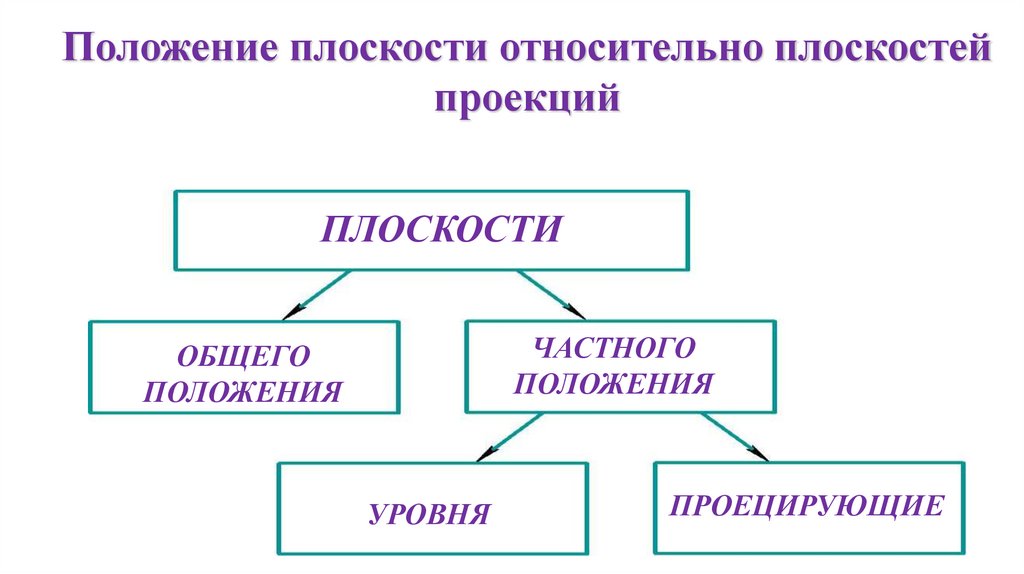
Положение плоскости относительно плоскостей
проекций
ПЛОСКОСТИ
ЧАСТНОГО
ПОЛОЖЕНИЯ
ОБЩЕГО
ПОЛОЖЕНИЯ
УРОВНЯ
ПРОЕЦИРУЮЩИЕ

22.

Плоскость общего положения
Плоскость непараллельная и неперпендикулярная плоскостям проекций

23.

Плоскости частного положения
Это плоскости параллельные или перпендикулярные
одной из плоскостей проекций

24.

Проецирующие плоскости
Это плоскости перпендикулярные одной
из плоскостей проекций

25.

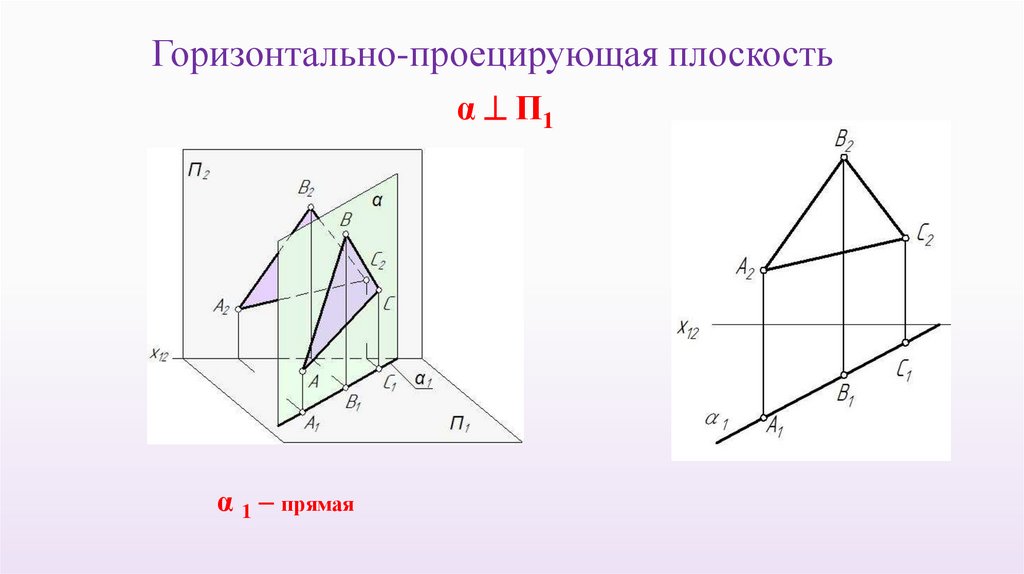
Горизонтально-проецирующая плоскость
α П1
α 1 – прямая

26.

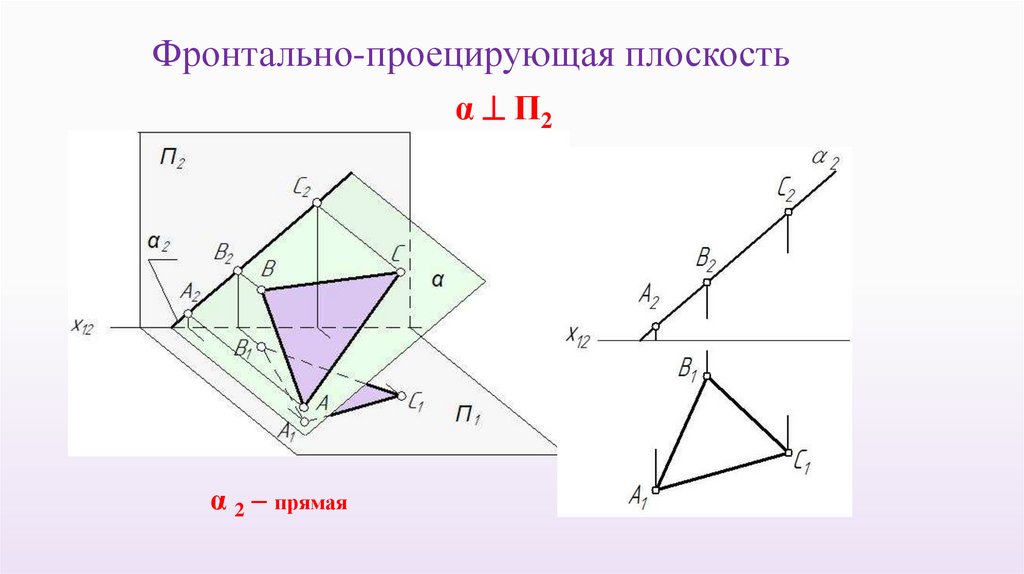
Фронтально-проецирующая плоскость
α П2
α 2 – прямая

27.

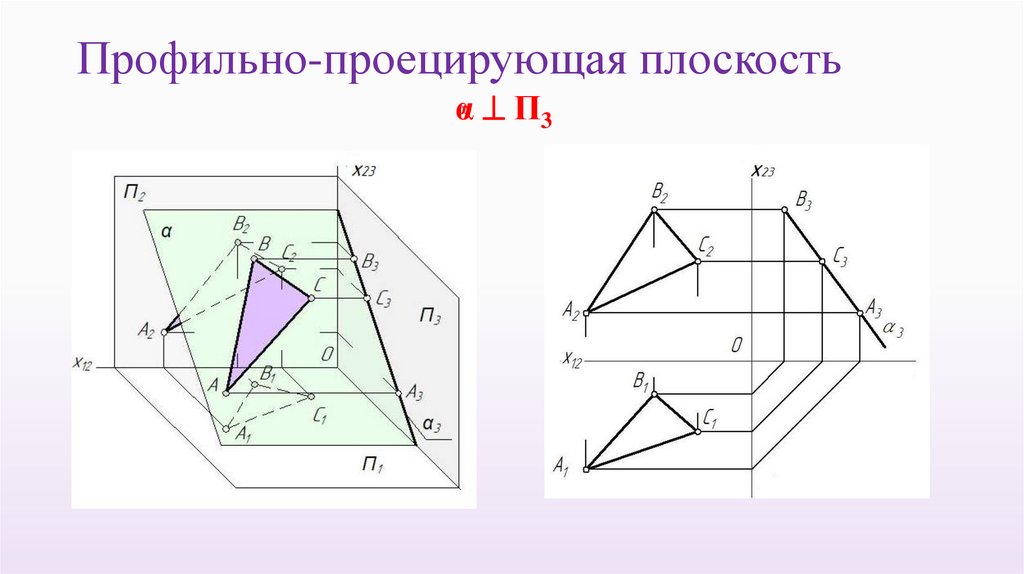
Профильно-проецирующая плоскость
α П
α
3

28.

Плоскости уровня
Это плоскости параллельные одной из
плоскостей проекций

29.

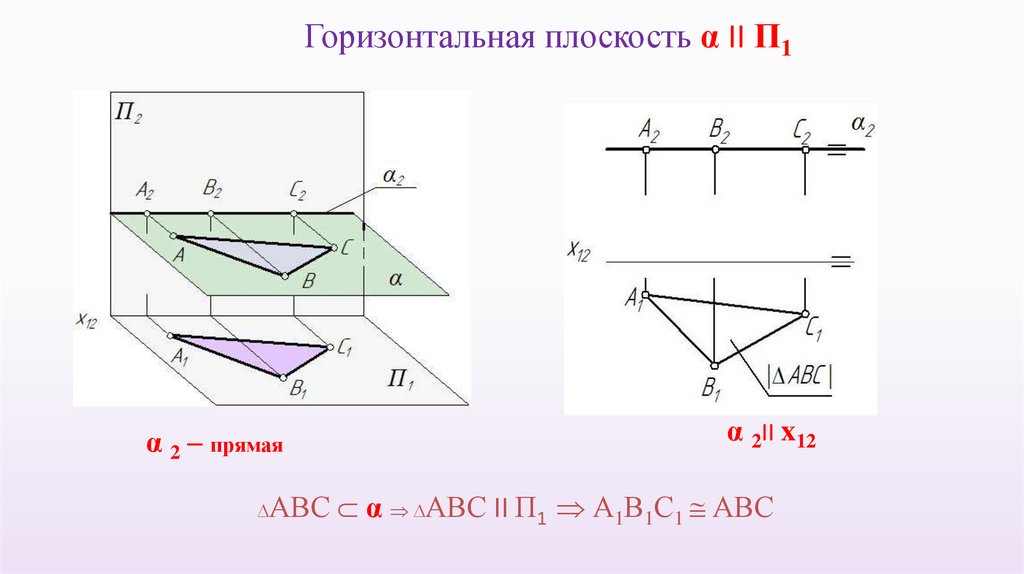
Горизонтальная плоскость α II П1
α 2 – прямая
α 2II x12
АВС α АВС II П1 А1В1С1 АВС

30.

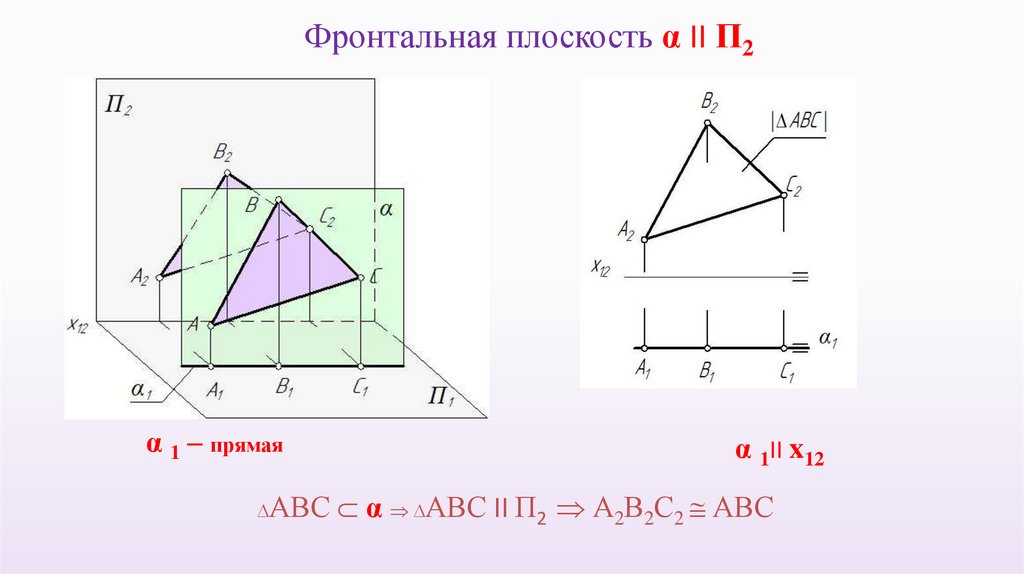
Фронтальная плоскость α II П2
α 1 – прямая
α 1II x12
АВС α АВС II П2 А2В2С2 АВС

31.

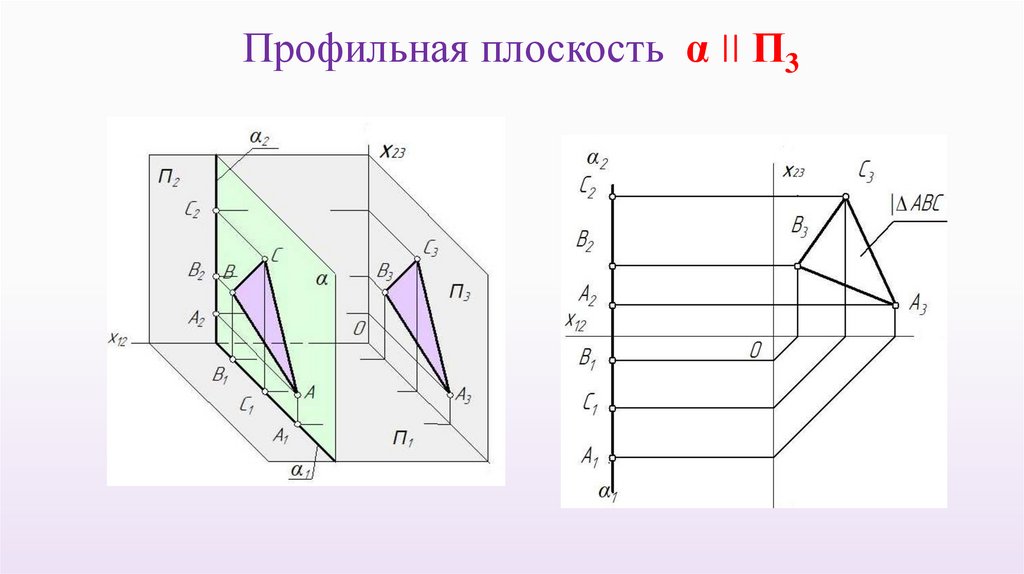
Профильная плоскость α II П3

32.

У плоскости частного положения одна из проекций
обязательно имеет форму прямой линии.

33.

Прямая линия
в плоскости

34.

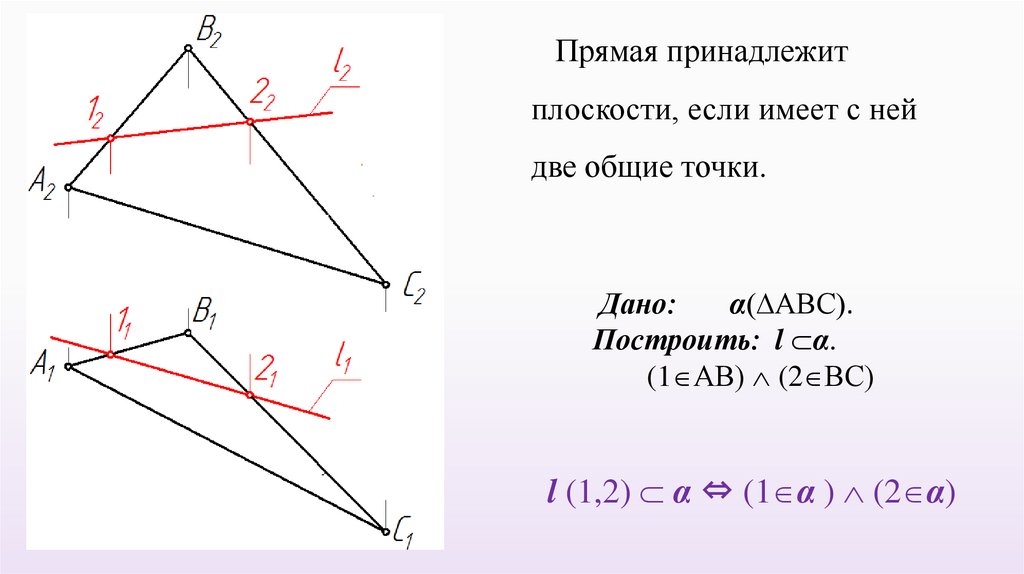
Прямая принадлежит
плоскости, если имеет с ней
две общие точки.
Дано:
α АВС .
Построить: l α.
(1 АВ) (2 ВС)
l (1,2) α ⇔ (1 α ) (2 α)

35.

Прямая принадлежит плоскости, если имеет
с плоскостью одну общую точку и
параллельна какой-либо прямой
расположенной в этой плоскости.
Дано:
α АВС .
Построить: l α.
(1 АВ) (2 АС; 2≡2∞) l ||АС
l (1,s) 1 l l ||s

36.

Главные линии плоскости
К главным линиям плоскости относятся прямые уровня горизонталь, фронталь и линии наибольшего наклона
плоскости.

37.

Горизонталь плоскости
Это прямая, принадлежащая плоскости,
и параллельная горизонтальной плоскости
проекций
Дано:
α АВС .
Построить: h α.
h 1 h2 x12
h (А,1)

38.

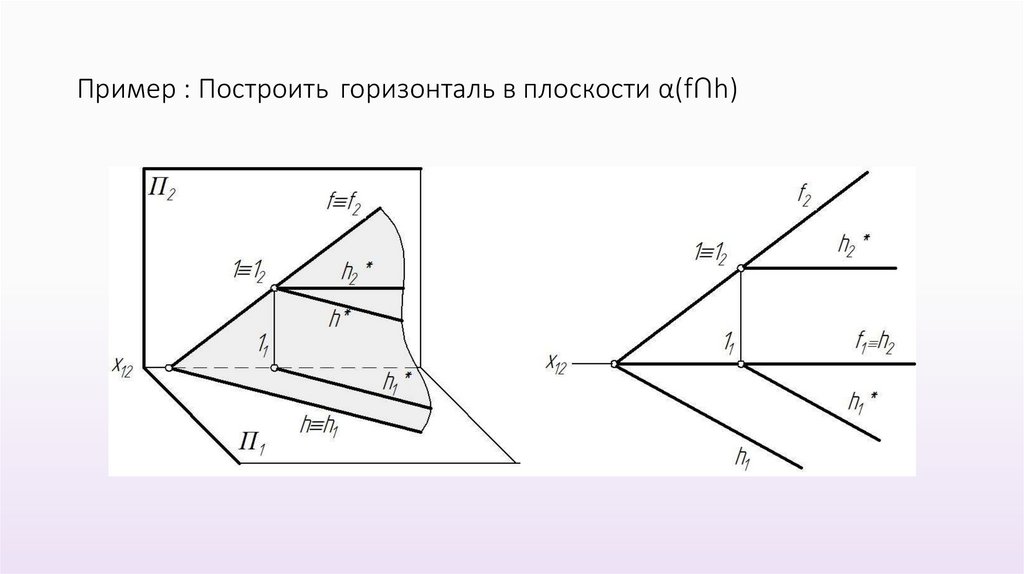
Пример : Построить горизонталь в плоскости α(f∩h)

39.

Фронталь плоскости
Это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости
проекций
Дано:
α АВС .
Построить: f α
f 2 f1 x12
f (А,1)

40.

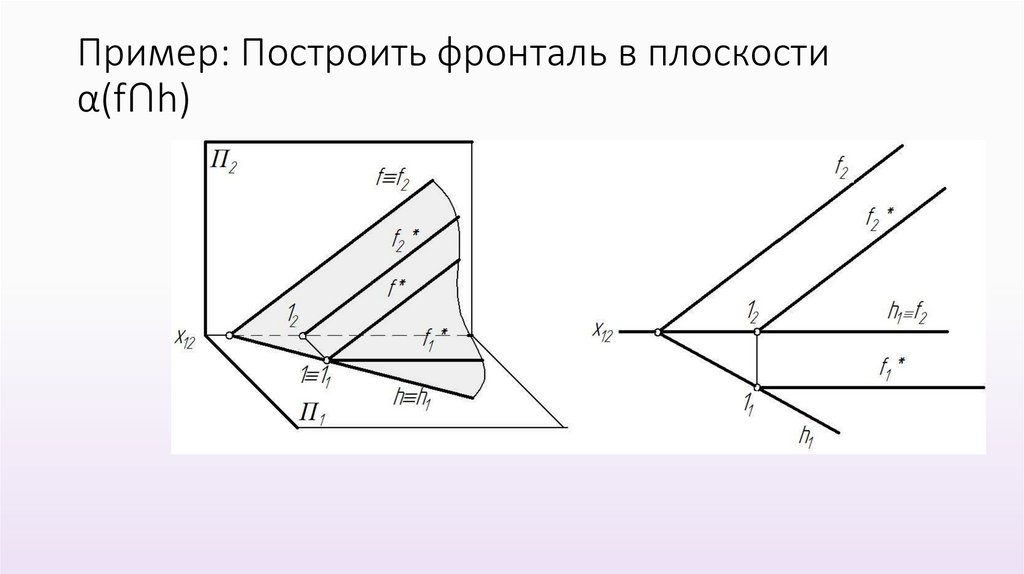
Пример: Построить фронталь в плоскости
α(f∩h)

41.

Точка в плоскости
Точка принадлежит плоскости, если она находится на прямой,
принадлежащей этой плоскости
А γ А l,l γ

42.

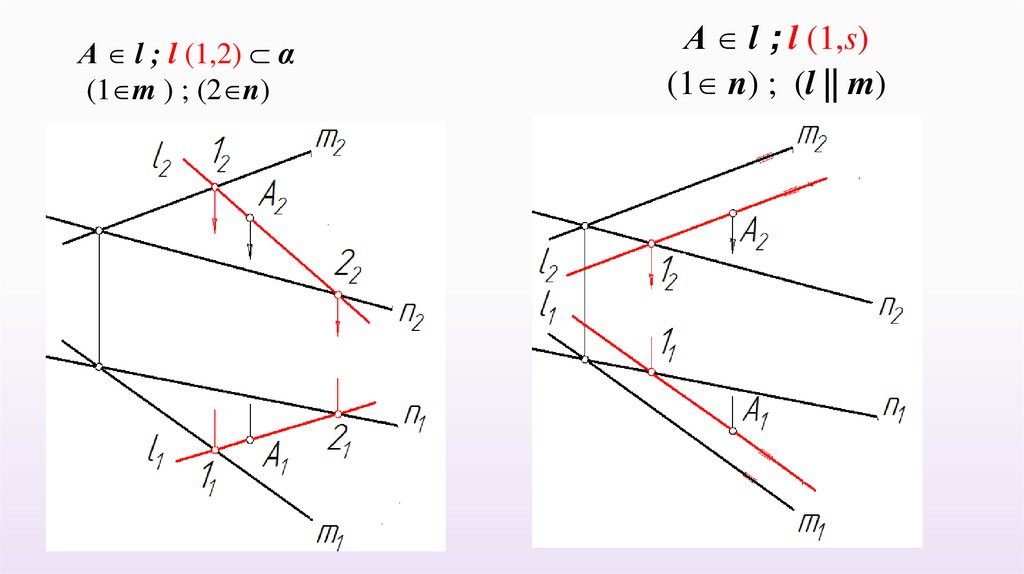
А l ; l (1,2) α
(1 m ) ; (2 n)
А l ; l (1,s)
(1 n) ; (l || m)

43.

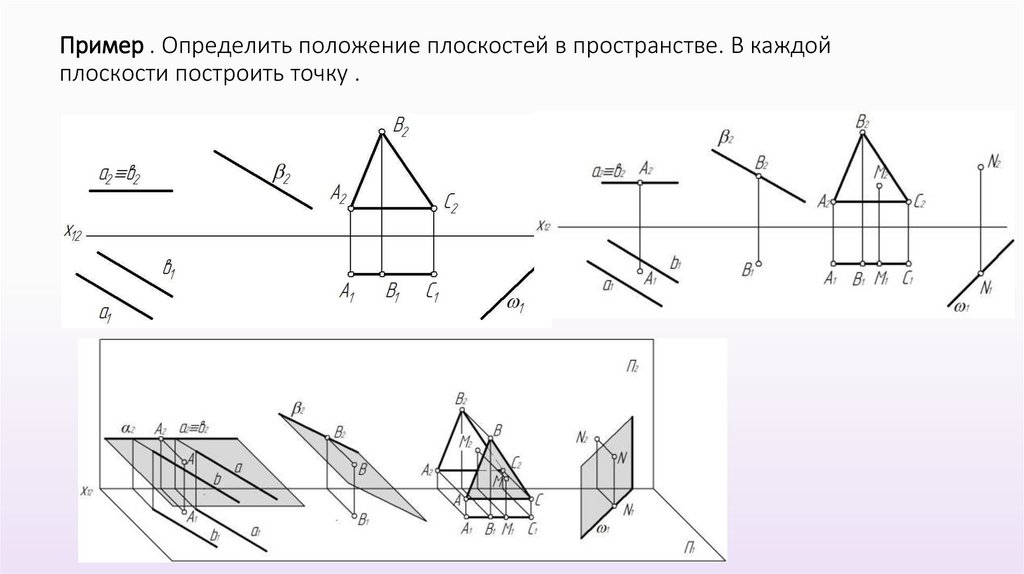
Пример . Определить положение плоскостей в пространстве. В каждой
плоскости построить точку .

44.

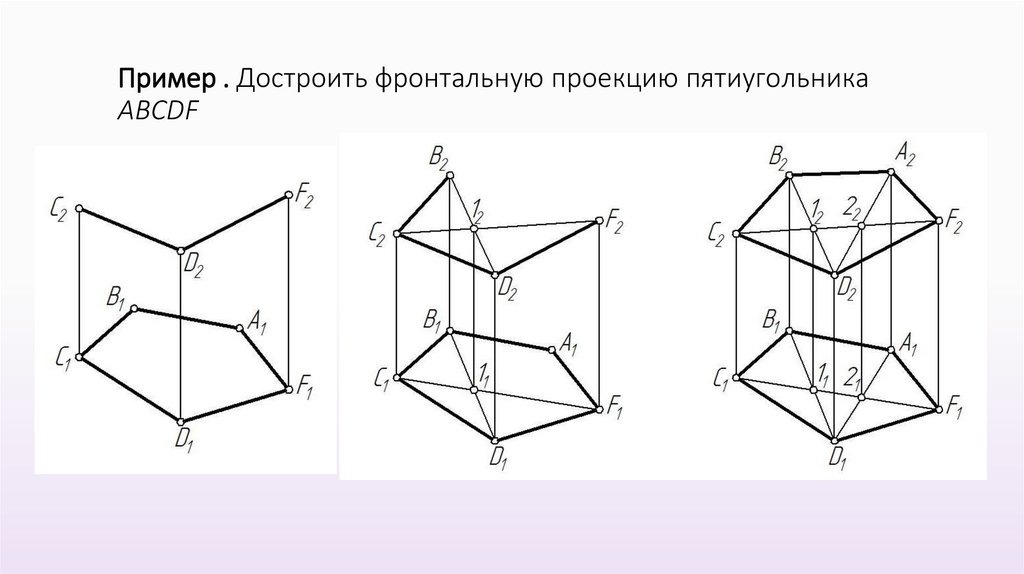
Пример . Достроить фронтальную проекцию пятиугольника
АВСDF

45.

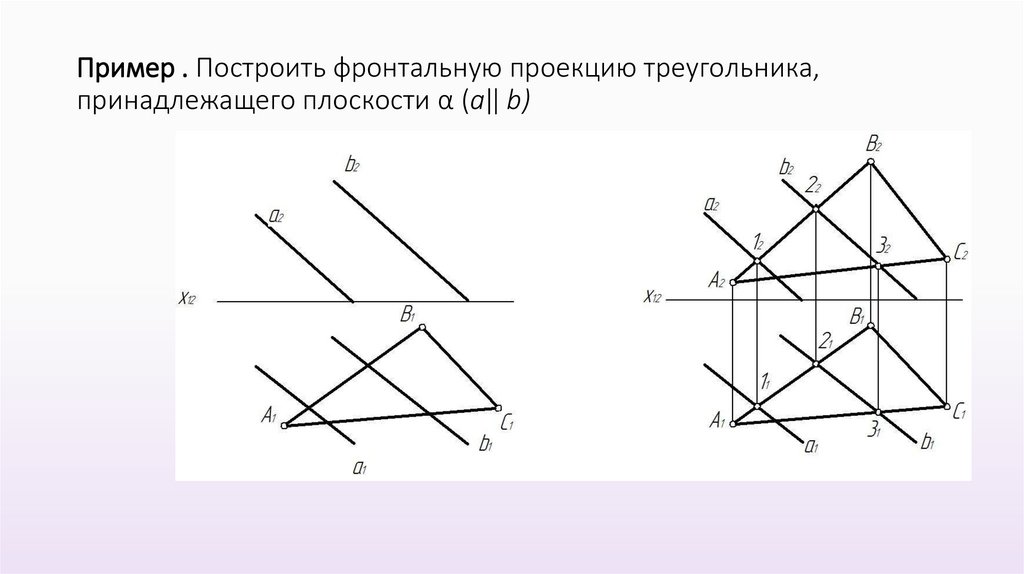
Пример . Построить фронтальную проекцию треугольника,
принадлежащего плоскости α (а‖ b)

46.

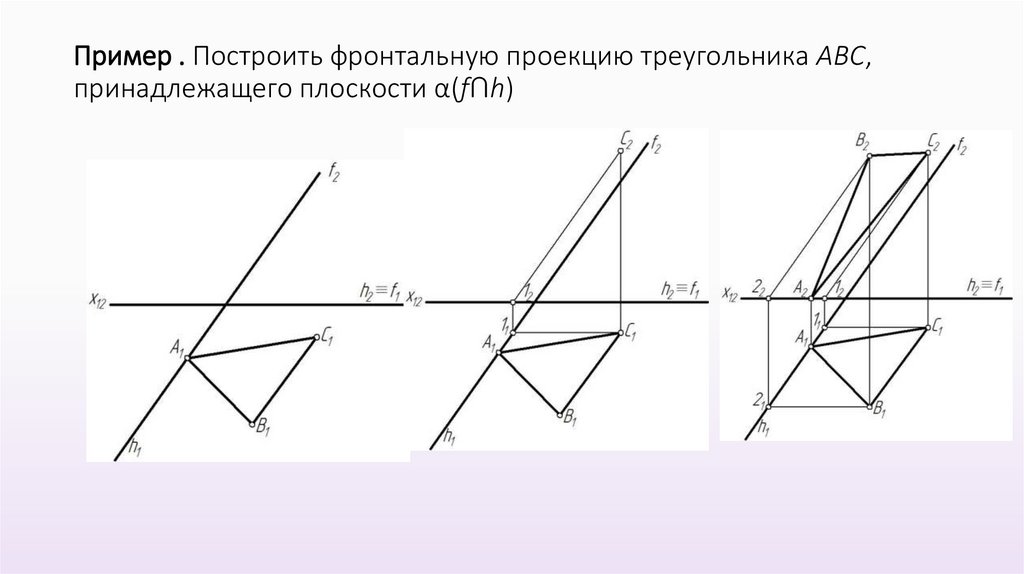
Пример . Построить фронтальную проекцию треугольника АВС,
принадлежащего плоскости α(f∩h)

47.

Взаимное положение двух плоскостей,
прямой и плоскости

48.

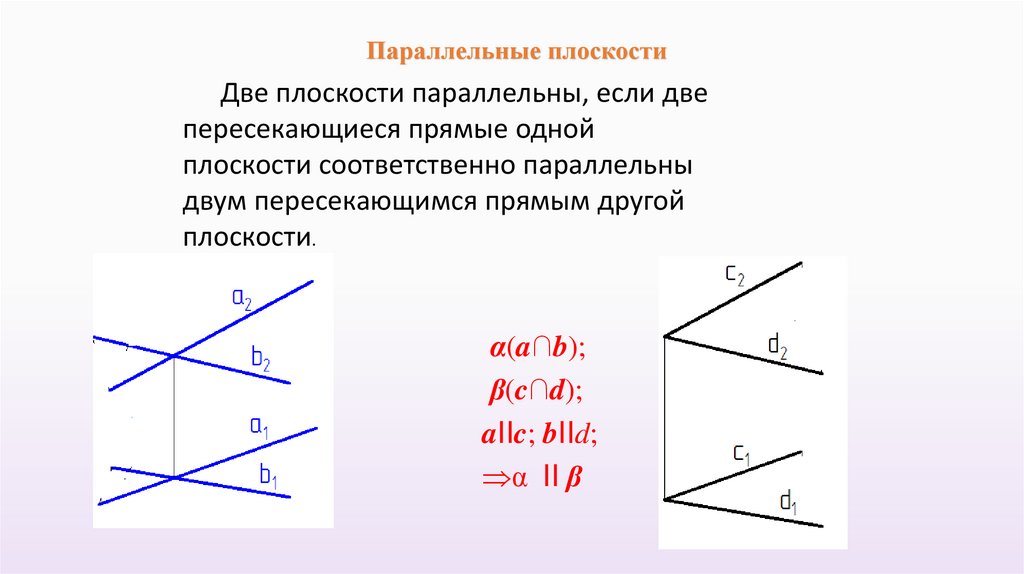
Параллельные плоскости
Две плоскости параллельны, если две
пересекающиеся прямые одной
плоскости соответственно параллельны
двум пересекающимся прямым другой
плоскости.
α(a∩b);
β(c∩d);
aIIc; bIId;
α II β

49.

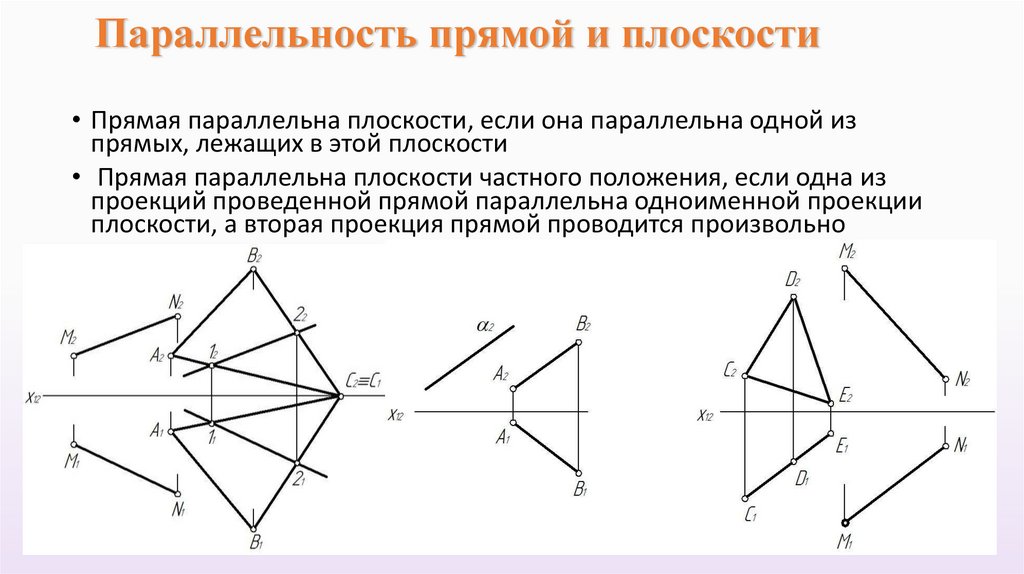
Параллельность прямой и плоскости
• Прямая параллельна плоскости, если она параллельна одной из
прямых, лежащих в этой плоскости
• Прямая параллельна плоскости частного положения, если одна из
проекций проведенной прямой параллельна одноименной проекции
плоскости, а вторая проекция прямой проводится произвольно