Начертательная геометрия. Проекции точки, прямой и плоскости

1. Дисциплина: ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА Раздел: «Начертательная геометрия»

Лекция 2
Уральский федеральный университет
имени первого Президента РФ Б.Н. Ельцина
Кафедра «Инженерная графика»
Дисциплина: ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА
Раздел: «Начертательная геометрия»
Тема 2. Проекции
точки, прямой и
плоскости
Лектор: Стриганова Лариса Юрьевна, к.п.н., доцент

2. Цель и задачи лекции

• Определить основы построения
ортогонального чертежа (эпюра)
• Дать понятия проекций точки, прямой
линии и плоскости на эпюре
• Раскрыть сущность построения точки,
прямой линии и плоскости в системе двух и
трех плоскостей проекций
Лекция 2. Проекции точки, прямой и
плоскости
2

3. В результате изучения темы Вы будете знать

• Сущность построения ортогонального чертежа (эпюра)
точки и прямой линии
• Способы задания прямой линии и плоскости на эпюре
• Приемы построения точки и прямой линии,
принадлежащих плоскости
В результате изучения темы Вы будете уметь:
• Строить и обозначать на эпюре проекции точки, прямой
линии и плоскости
Лекция 2. Проекции точки, прямой и
плоскости
3

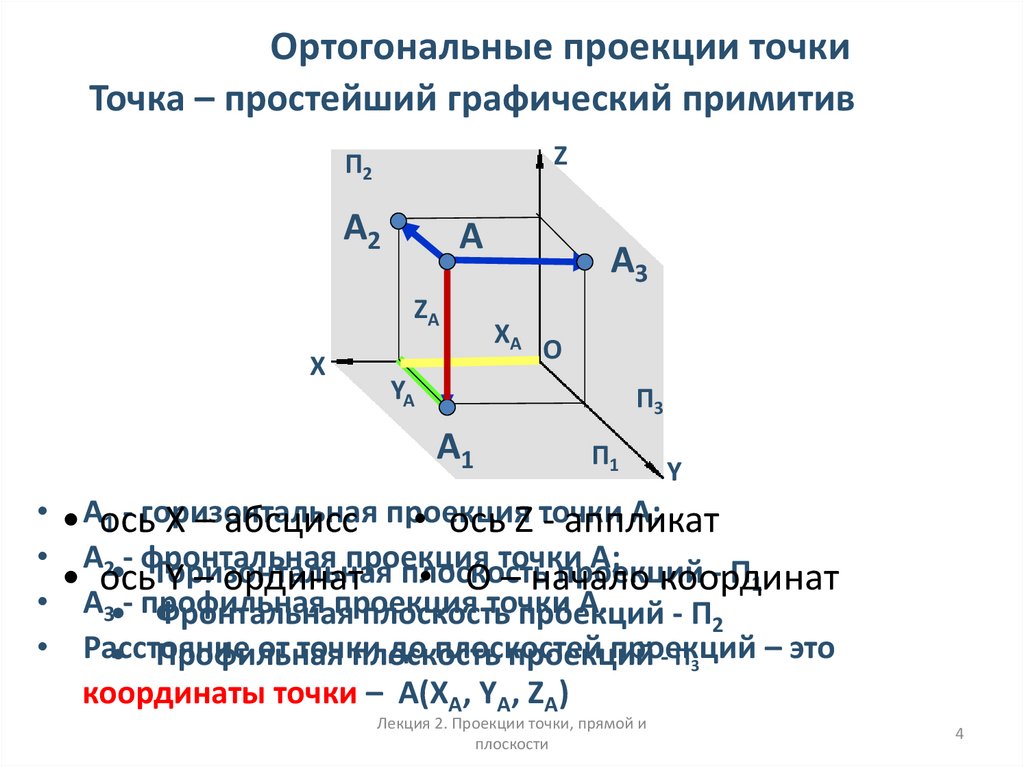
4. Ортогональные проекции точки

Точка – простейший графический примитив
Z
П2
А2
А
ZA
X
XA
O
YA
П3
А1
А3
П1
Y
А;
1 - горизонтальная
• Аось
X – абсцисс проекция
• ось Z точки
- аппликат
А2•- фронтальная
проекция
точки
А;
Горизонтальная
плоскость
проекций
- П1
• ось Y – ординат • О – начало координат
А3•- профильная
проекция
точки
А.
Фронтальная
плоскость
проекций
- П2
Расстояние
от точки
до плоскостей
проекций
– это
• Профильная
плоскость
проекций
- П3
координаты точки – А(XА, YА, ZА)
Лекция 2. Проекции точки, прямой и
плоскости
4

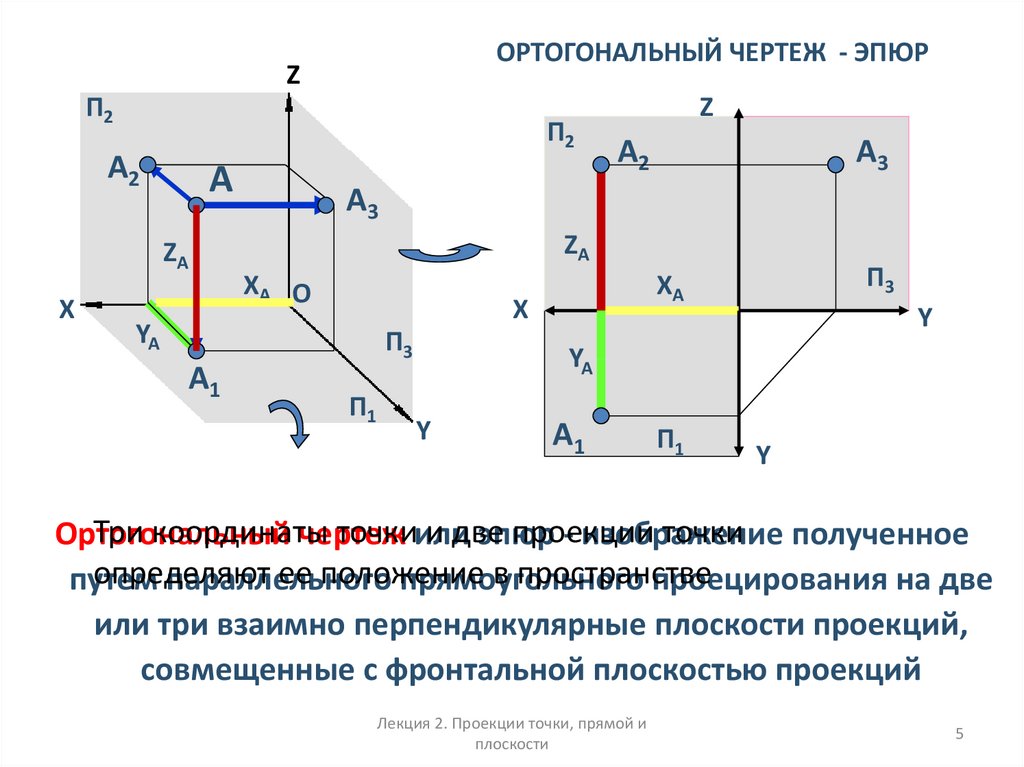
5. ОРТОГОНАЛЬНЫЙ ЧЕРТЕЖ - ЭПЮР

Z
П2
П2
А2
А
ZA
X
А2
А3
А3
ZA
XA O
П3
П1
П3
XA
X
YA
А1
Z
Y
YA
Y
А1
П1
Y
Три координаты
точкиили
и две
проекции
точки полученное
Ортогональный
чертеж
эпюр
- изображение
определяют
ее положение
в пространстве
путем
параллельного
прямоугольного
проецирования на две
или три взаимно перпендикулярные плоскости проекций,
совмещенные с фронтальной плоскостью проекций
Лекция 2. Проекции точки, прямой и
плоскости
5

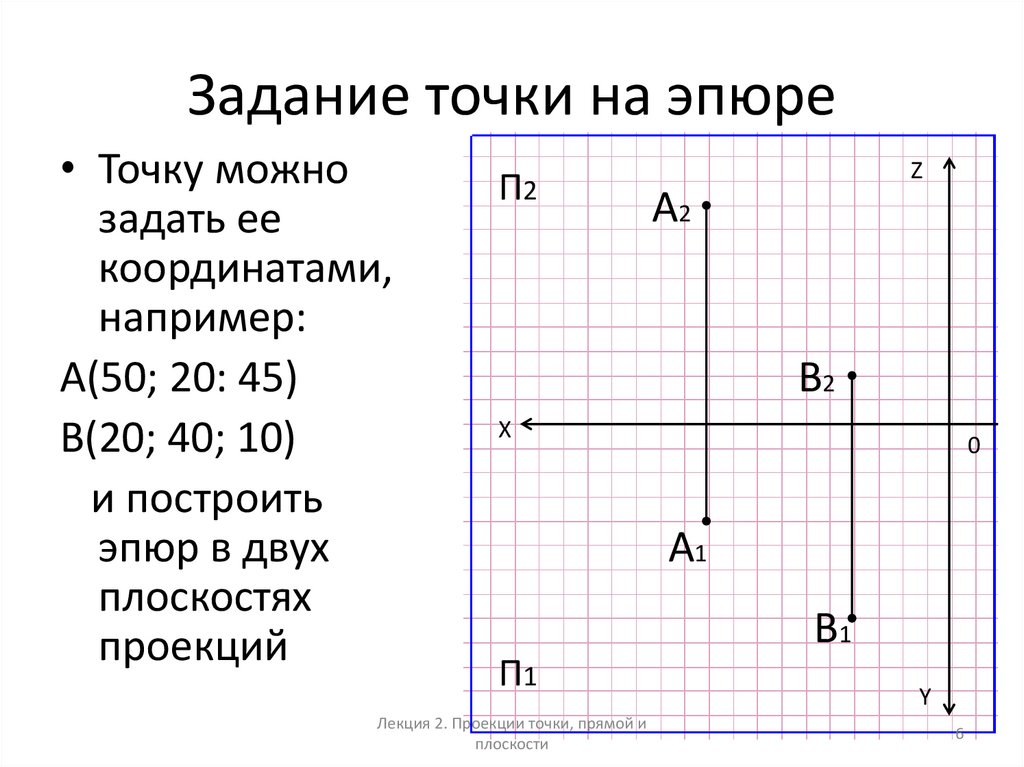
6. Задание точки на эпюре

• Точку можно
задать ее
координатами,
например:
А(50; 20: 45)
В(20; 40; 10)
и построить
эпюр в двух
плоскостях
проекций
П2
Z
A2
B2
X
0
A1
B1
П1
Лекция 2. Проекции точки, прямой и
плоскости
Y
6

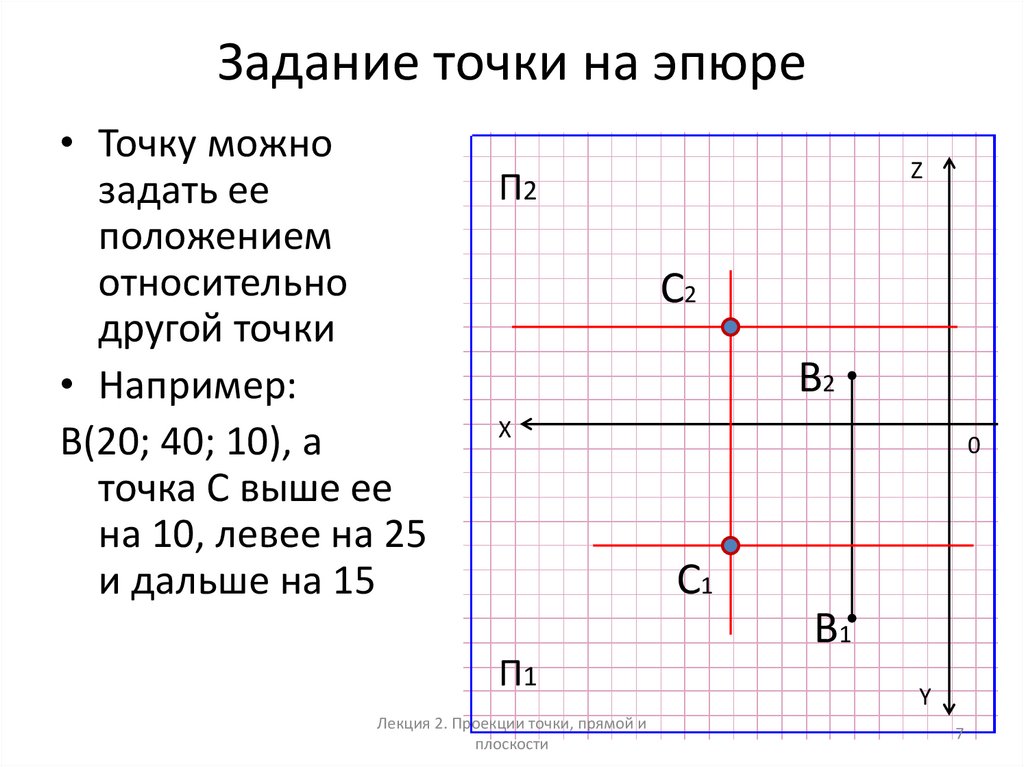
7. Задание точки на эпюре

• Точку можно
задать ее
положением
относительно
другой точки
• Например:
В(20; 40; 10), а
точка С выше ее
на 10, левее на 25
и дальше на 15
Z
П2
С2
B2
X
0
С1
B1
П1
Лекция 2. Проекции точки, прямой и
плоскости
Y
7

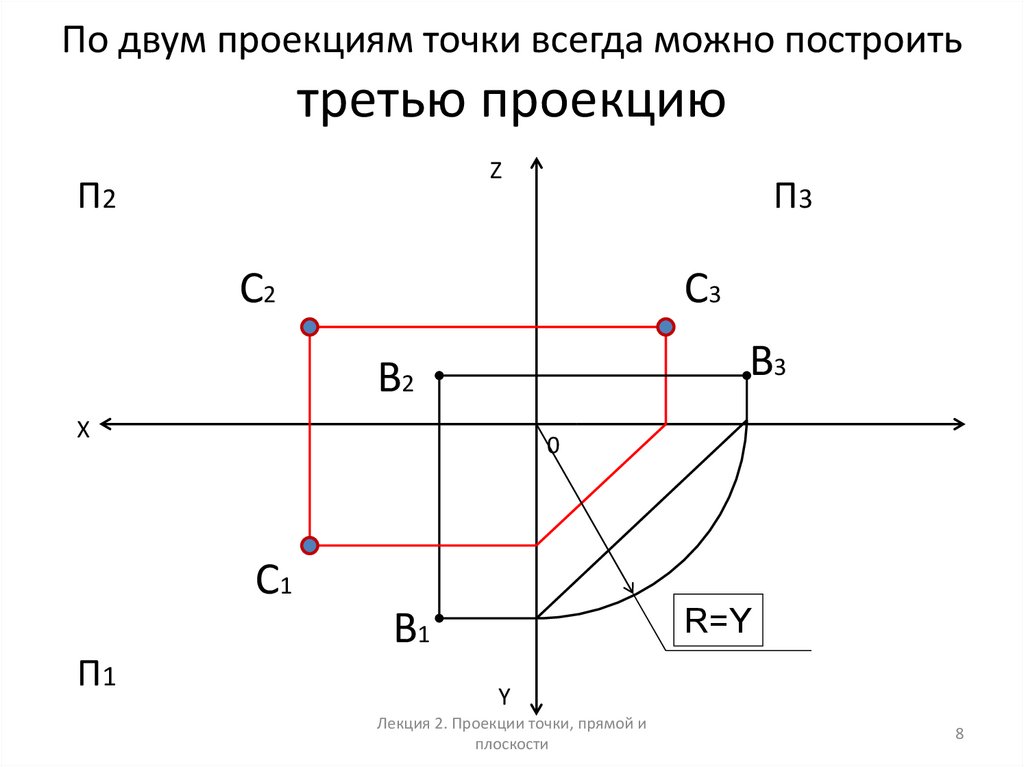
8. По двум проекциям точки всегда можно построить третью проекцию

Z
П2
П3
С2
С3
B3
B2
X
0
С1
B1
П1
R=Y
Y
Лекция 2. Проекции точки, прямой и
плоскости
8

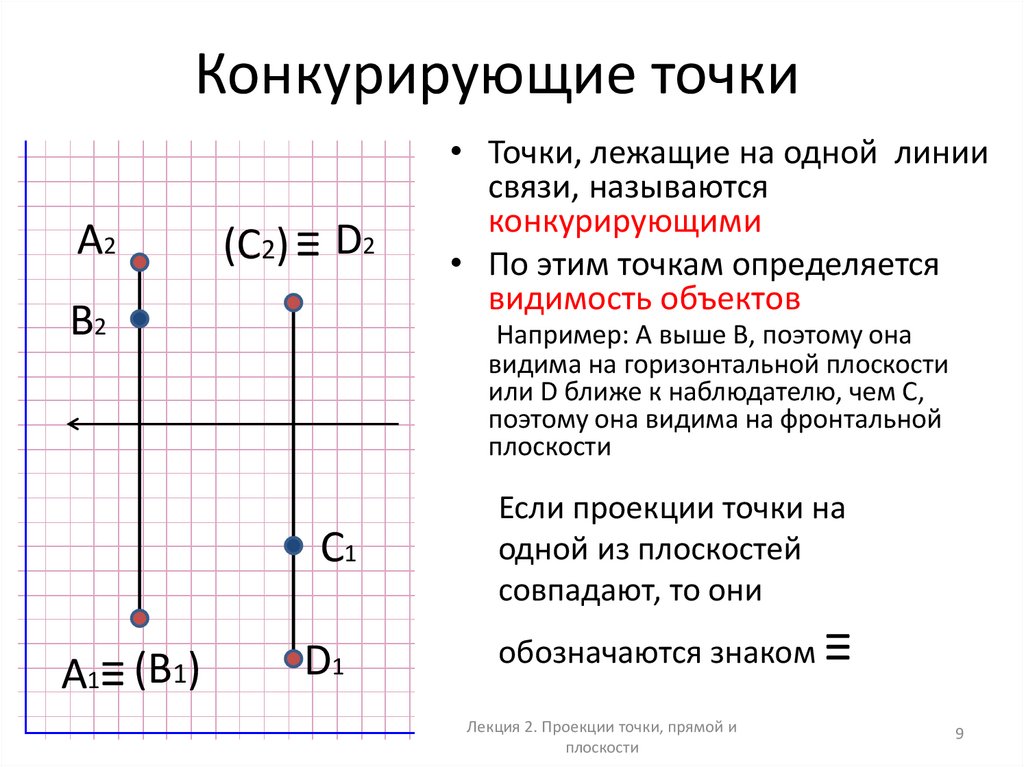
9. Конкурирующие точки

А2
(С2) ≡ D2
В2
Например: А выше В, поэтому она
видима на горизонтальной плоскости
или D ближе к наблюдателю, чем С,
поэтому она видима на фронтальной
плоскости
С1
А1≡ (В1)
• Точки, лежащие на одной линии
связи, называются
конкурирующими
• По этим точкам определяется
видимость объектов
D1
Если проекции точки на
одной из плоскостей
совпадают, то они
обозначаются знаком
Лекция 2. Проекции точки, прямой и
плоскости
≡
9

10. Прямая линия – кратчайшее расстояние между двумя точками

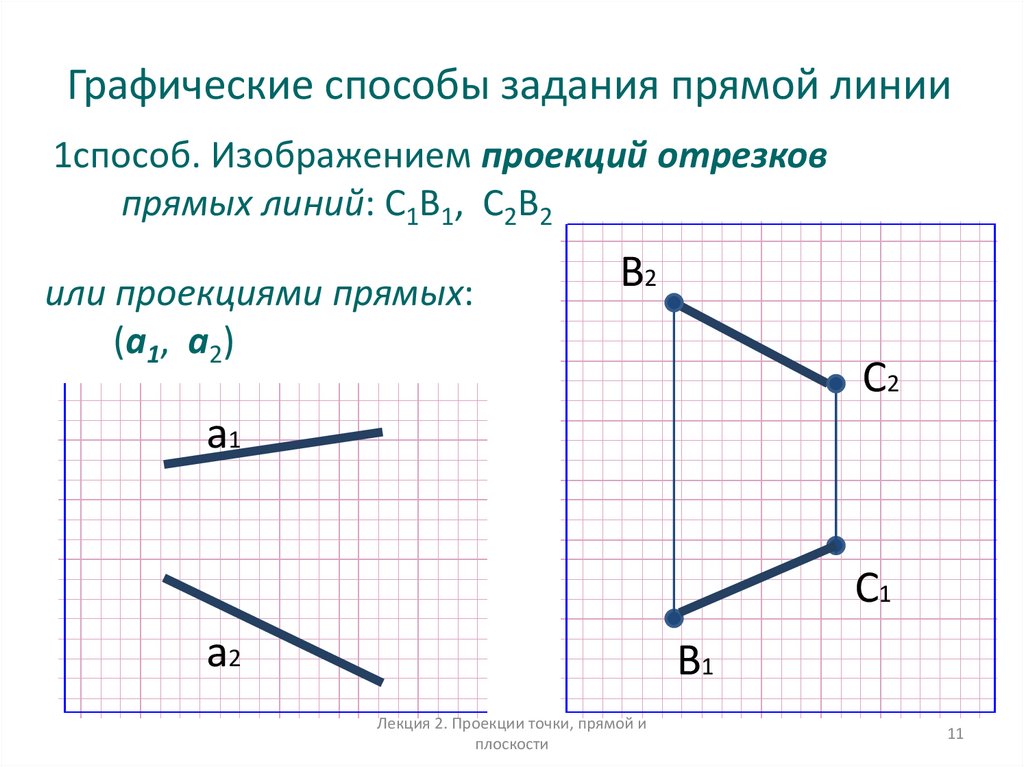
11. Графические способы задания прямой линии

1способ. Изображением проекций отрезков
прямых линий: C1B1, C2B2
или проекциями прямых:
(а1, а2)
B2
С2
а1
С1
а2
B1
Лекция 2. Проекции точки, прямой и
плоскости
11

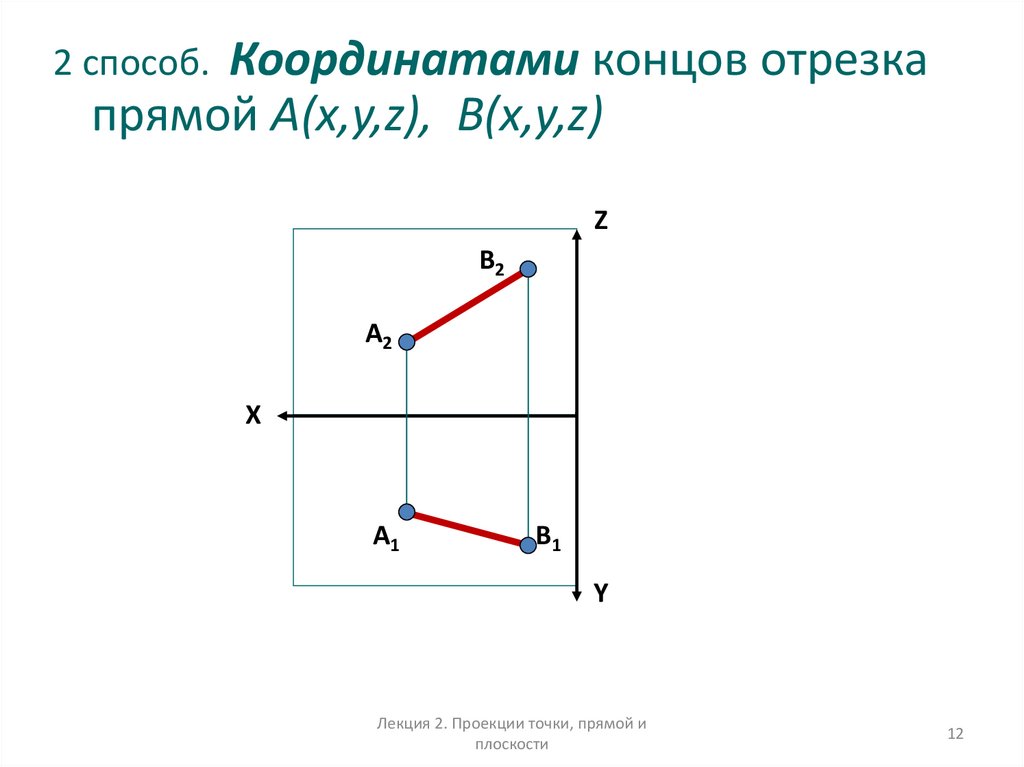
12.

Координатами концов отрезка
прямой А(x,y,z), В(x,y,z)
2 способ.
Z
В2
А2
X
А1
В1
Y
Лекция 2. Проекции точки, прямой и
плоскости
12

13.

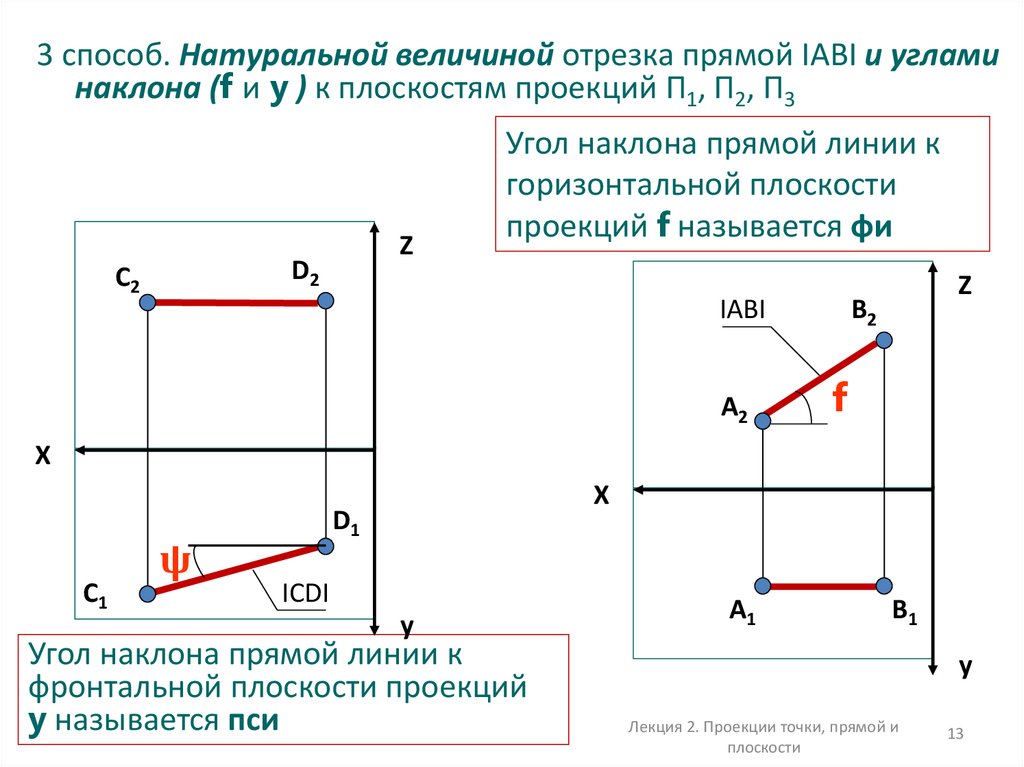
3 способ. Натуральной величиной отрезка прямой IABI и углами
наклона (f и y ) к плоскостям проекций П1, П2, П3
Z
D2
C2
Угол наклона прямой линии к
горизонтальной плоскости
проекций f называется фи
IАВI
А2
Z
В2
f
X
C1
ψ
X
D1
ICDI
y
Угол наклона прямой линии к
фронтальной плоскости проекций
y называется пси
А1
В1
y
Лекция 2. Проекции точки, прямой и
плоскости
13

14. Прямые в пространстве могут занимать общее и частное положение

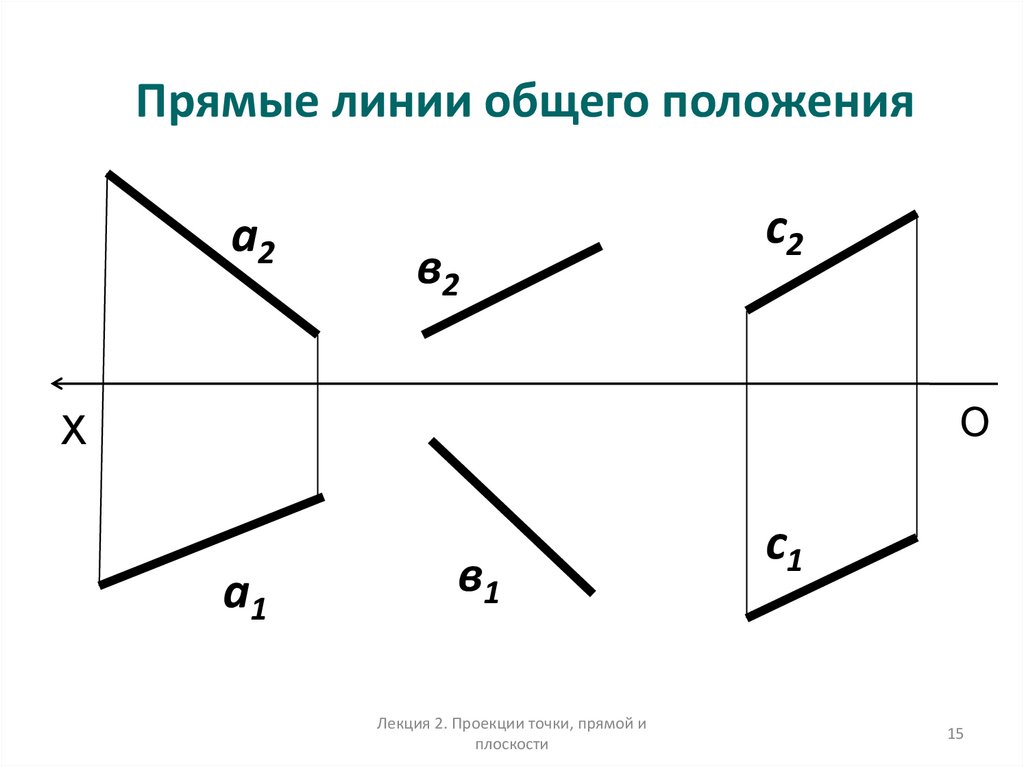
• Прямые общего
положения не
параллельны и не
перпендикулярны ни
одной из плоскостей
проекций
• Прямые частного
положения либо
параллельны, либо
перпендикулярны
плоскостям проекций
Лекция 2. Проекции точки, прямой и
плоскости
14

15. Прямые линии общего положения

а2
в2
с2
О
Х
а1
в1
Лекция 2. Проекции точки, прямой и
плоскости
с1
15

16. Прямые линии частного положения

• прямые перпендикулярные плоскостям проекций
- проецирующие прямые
• прямые параллельные плоскостям проекций –
линии уровня
Лекция 2. Проекции точки, прямой и
плоскости
16

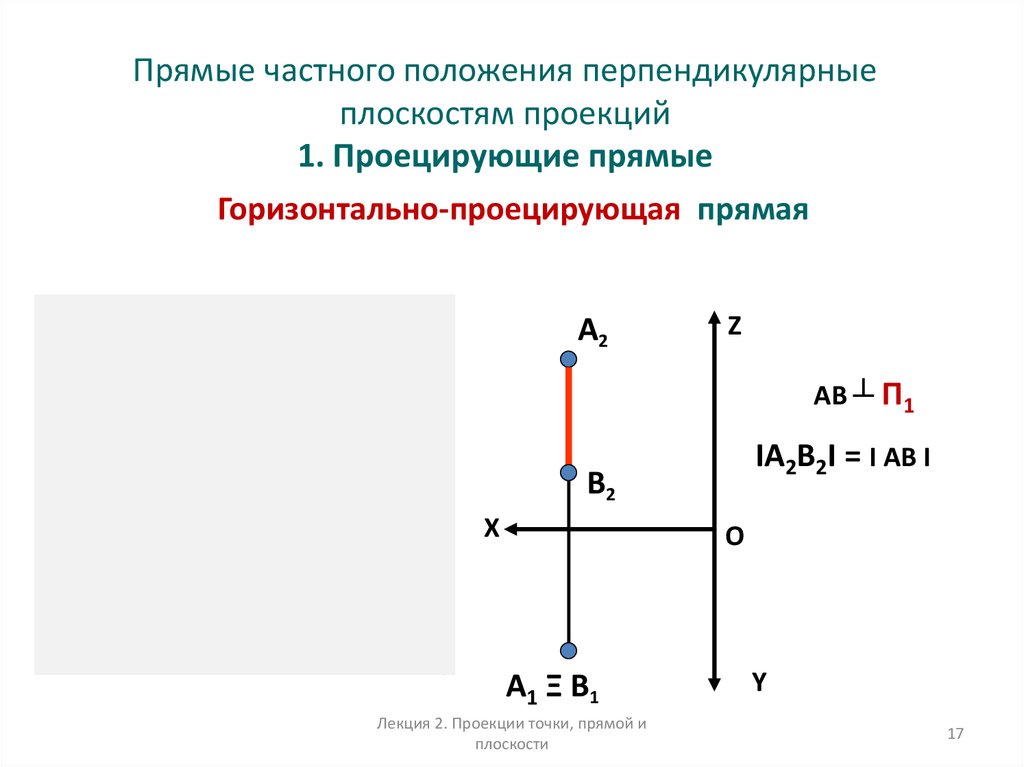
17. Прямые частного положения перпендикулярные плоскостям проекций 1. Проецирующие прямые

Горизонтально-проецирующая прямая
Z
А2
А2
Z
AB ┴ П1
А
B2
X
B
IА2В2I = I АВ I
B2
О
X
О
А1 Ξ B
1
Y
А1 Ξ B1
Лекция 2. Проекции точки, прямой и
плоскости
Y
17

18.

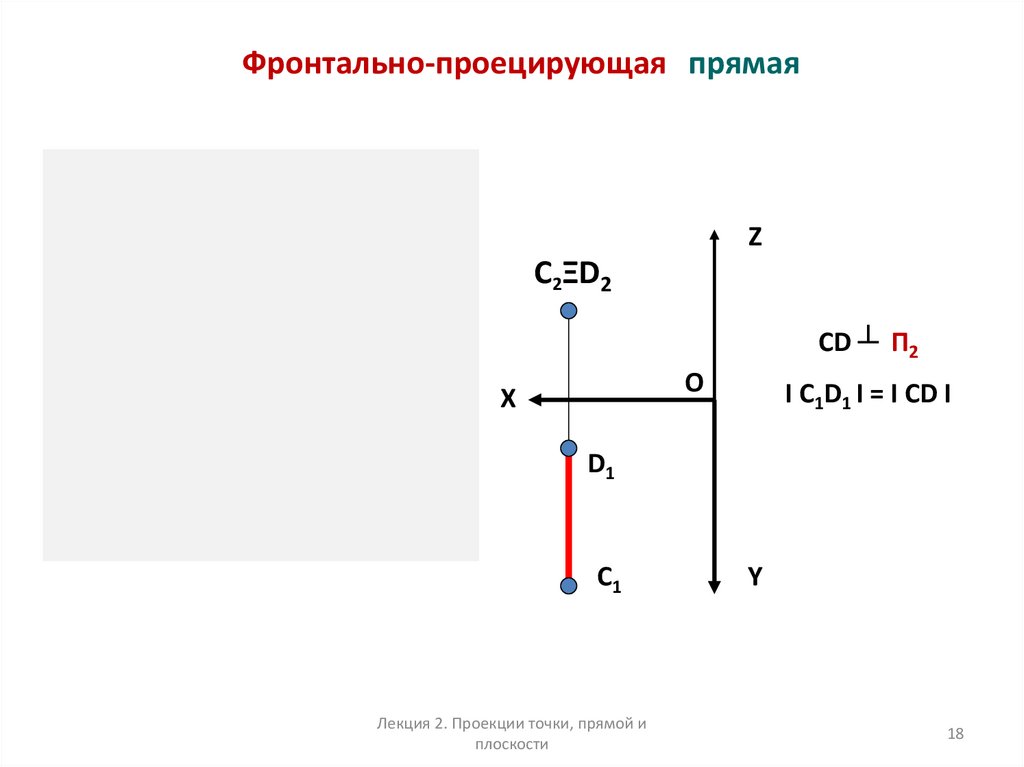
Фронтально-проецирующая прямая
Z
Z
C2ΞD2
C2 Ξ D2
D
CD ┴ П2
C
X
О
X
D1
I C1D1 I = I CD I
D1
C1
Y
C1
Лекция 2. Проекции точки, прямой и
плоскости
Y
18

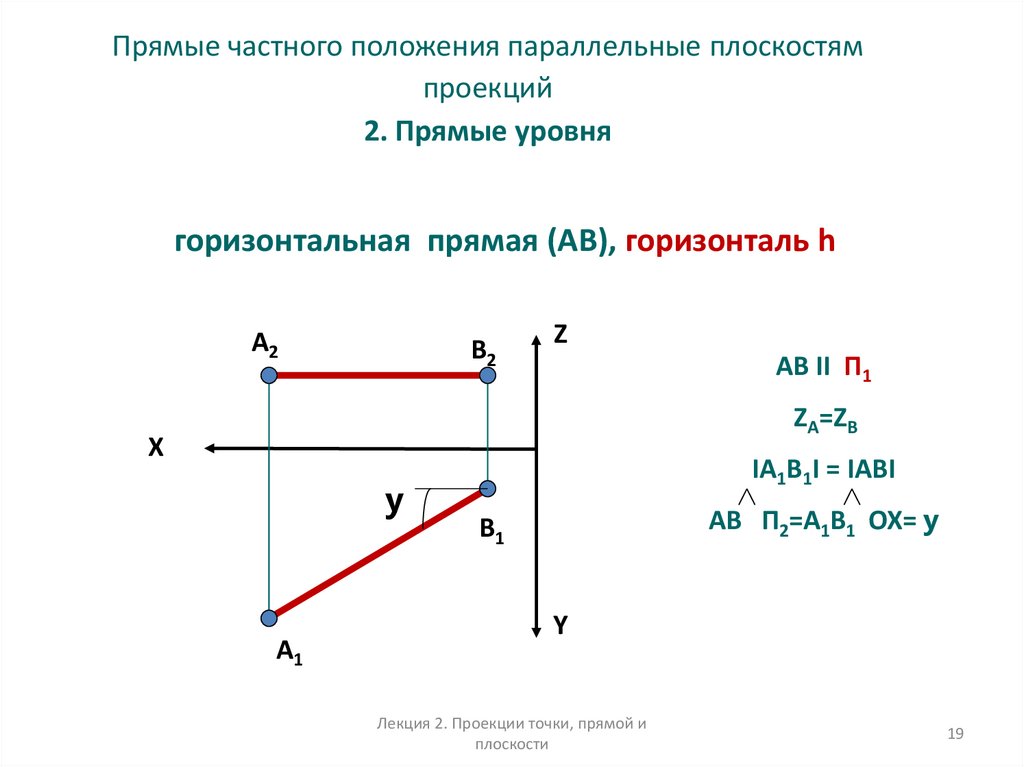
19. Прямые частного положения параллельные плоскостям проекций 2. Прямые уровня

горизонтальная прямая (AB), горизонталь h
А2
В2
Z
AВ II П1
ZА=ZB
X
y
А1
IА1В1I = IАВI
АВ П2=А1В1 OX= y
В1
Y
Лекция 2. Проекции точки, прямой и
плоскости
19

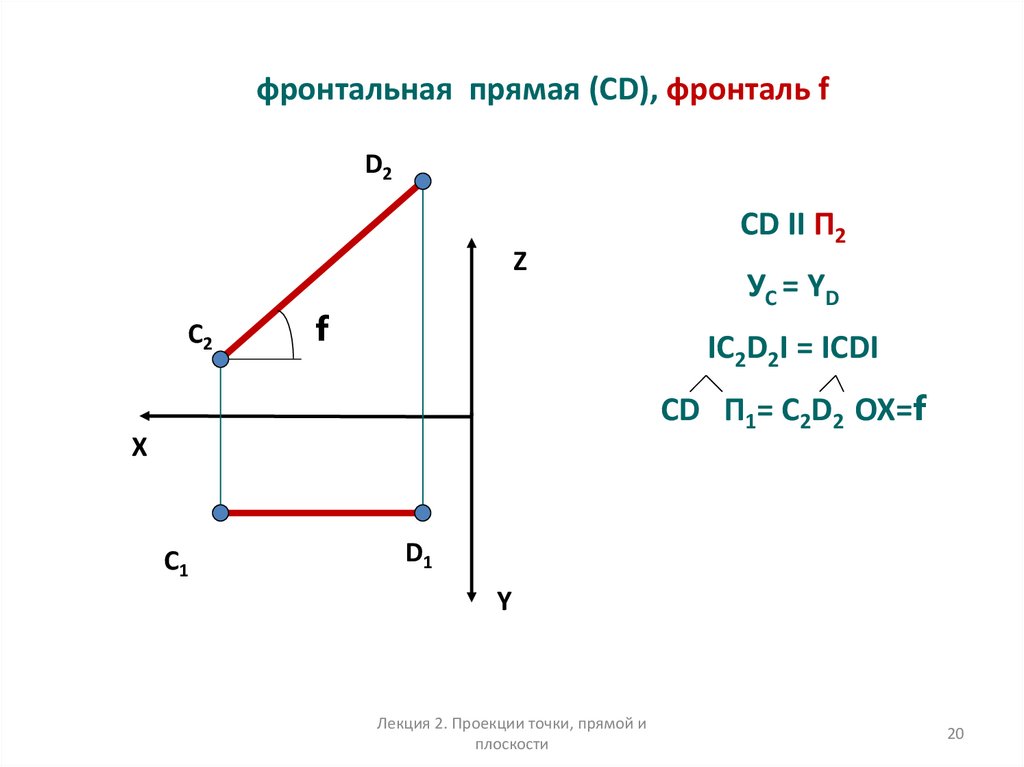
20.

фронтальная прямая (CD), фронталь f
D2
Z
C2
f
CD II П2
УС = YD
IС2D2I = ICDI
CD П1= С2D2 OX=f
X
C1
D1
Y
Лекция 2. Проекции точки, прямой и
плоскости
20

21. Относительное положение прямых

Прямые в пространстве могут быть расположены:
1. Параллельно
2. Перпендикулярно
3. Пересекаться
4. Скрещиваться
Лекция 2. Проекции точки, прямой и
плоскости
21

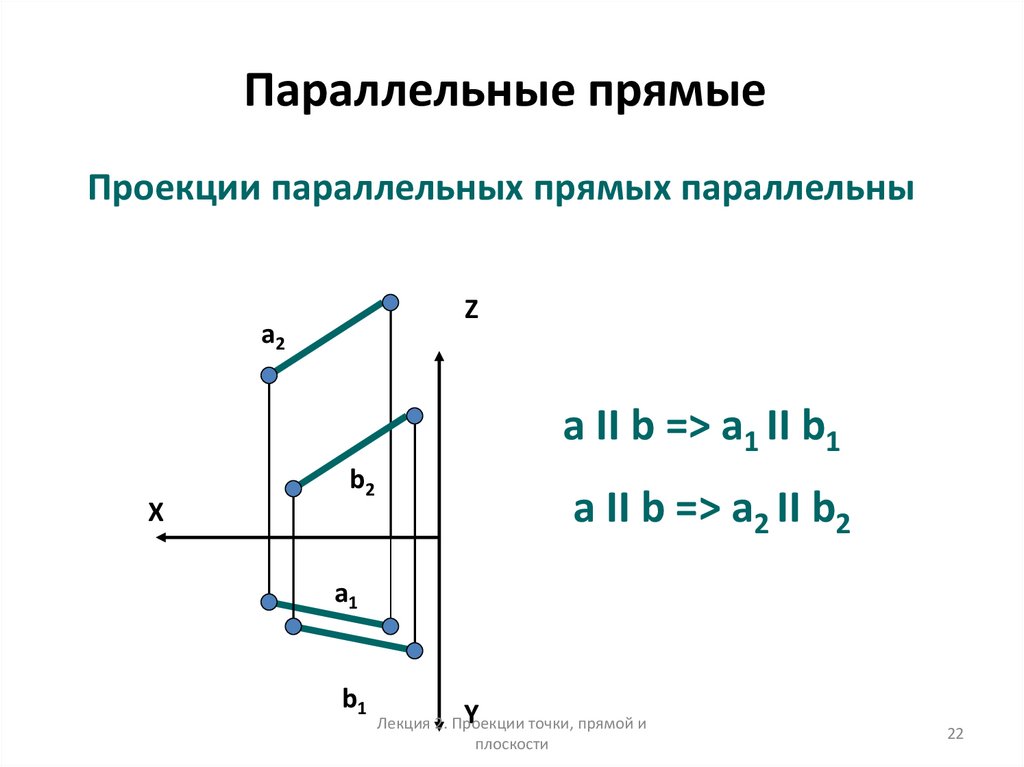
22. Параллельные прямые

Проекции параллельных прямых параллельны
Z
а2
a II b => a1 II b1
X
b2
a II b => a2 II b2
a1
b1
Y
Лекция 2. Проекции точки, прямой и
плоскости
22

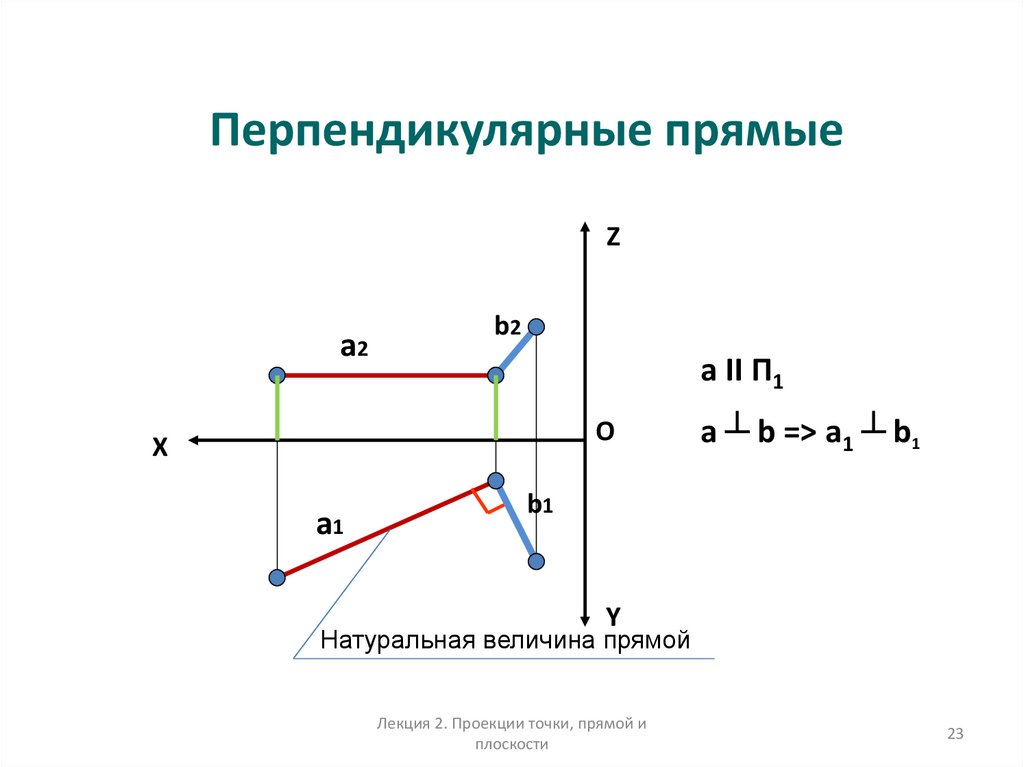
23. Перпендикулярные прямые

Z
a2
b2
a II П1
O
X
a1
a ┴ b => a1 ┴ b1
b1
Y
Натуральная величина прямой
Лекция 2. Проекции точки, прямой и
плоскости
23

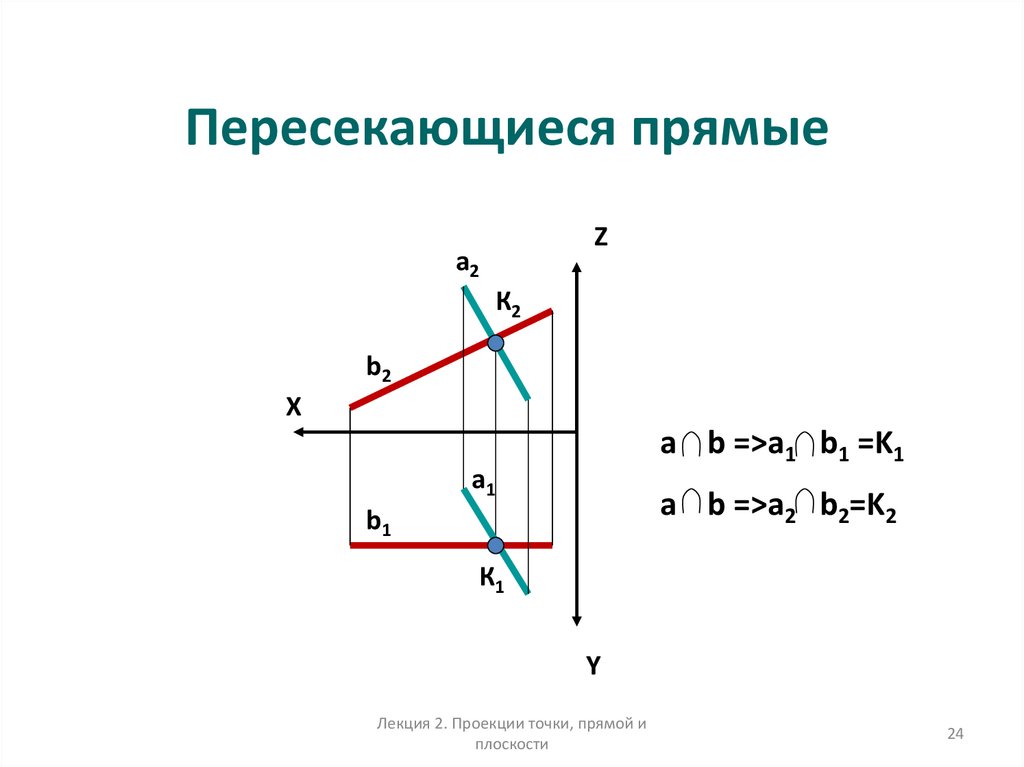
24. Пересекающиеся прямые

Z
a2
К2
b2
X
a b =>a1 b1 =K1
a1
a b =>a2 b2=K2
b1
К1
Y
Лекция 2. Проекции точки, прямой и
плоскости
24

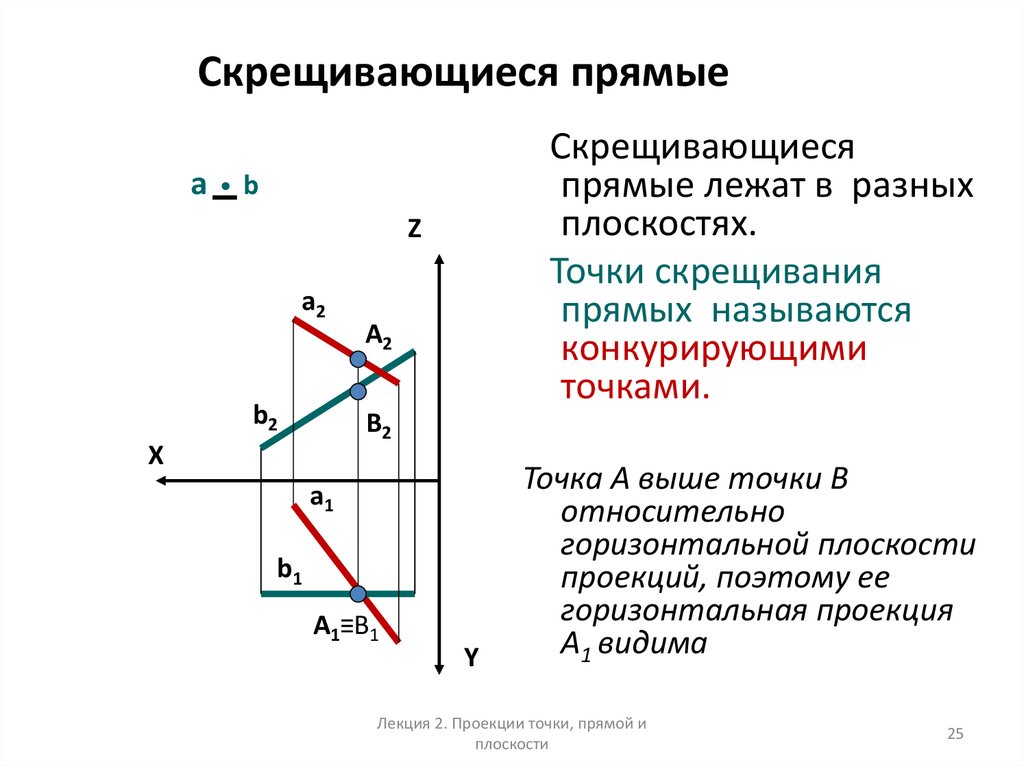
25. Скрещивающиеся прямые

a
Скрещивающиеся
прямые лежат в разных
плоскостях.
Точки скрещивания
прямых называются
конкурирующими
точками.
• b
Z
a2
b2
А2
В2
X
a1
b1
А1≡В1
Y
Точка А выше точки В
относительно
горизонтальной плоскости
проекций, поэтому ее
горизонтальная проекция
А1 видима
Лекция 2. Проекции точки, прямой и
плоскости
25

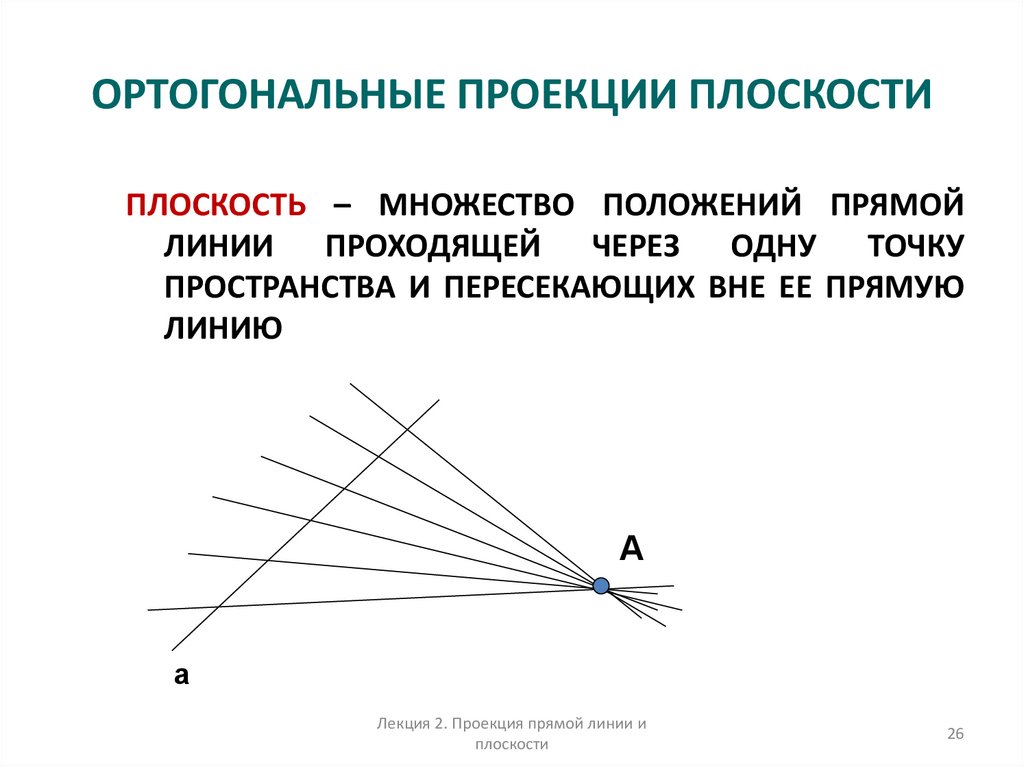
26. ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ПЛОСКОСТИ

ПЛОСКОСТЬ – МНОЖЕСТВО ПОЛОЖЕНИЙ ПРЯМОЙ
ЛИНИИ ПРОХОДЯЩЕЙ ЧЕРЕЗ ОДНУ ТОЧКУ
ПРОСТРАНСТВА И ПЕРЕСЕКАЮЩИХ ВНЕ ЕЕ ПРЯМУЮ
ЛИНИЮ
A
a
Лекция 2. Проекция прямой линии и
плоскости
26

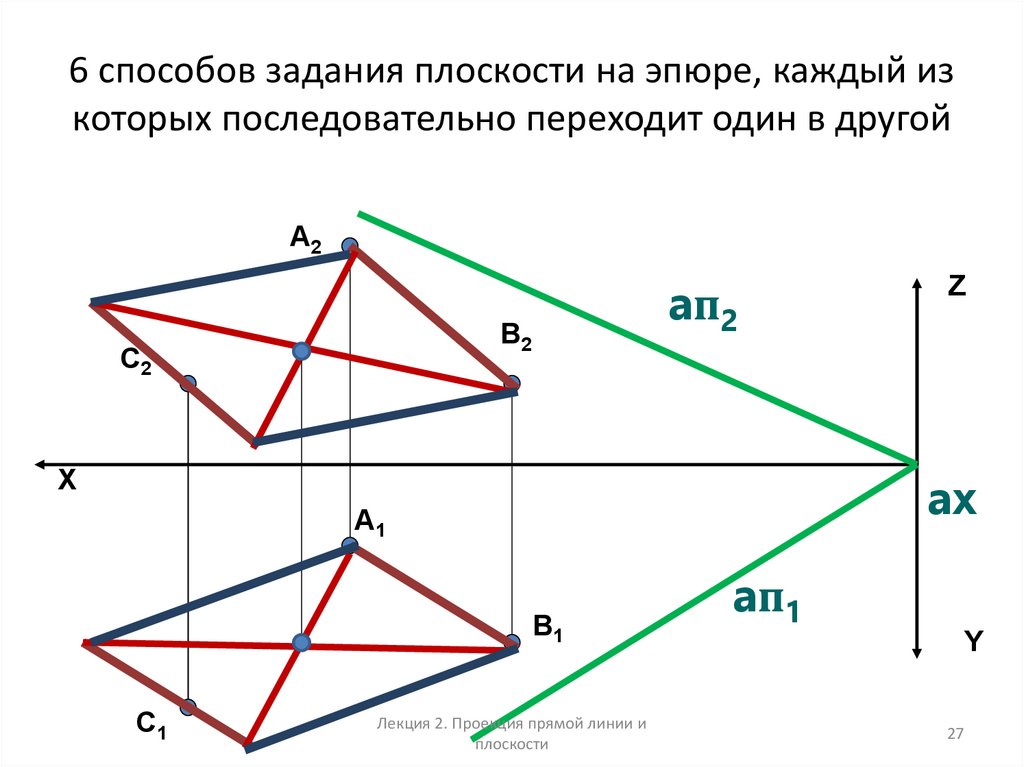
27. 6 способов задания плоскости на эпюре, каждый из которых последовательно переходит один в другой

А2
aп2
В2
C2
ax
X
А1
В1
C1
Z
Лекция 2. Проекция прямой линии и
плоскости
aп1
Y
27

28. Следом плоскости называется линия пересечения заданной плоскости с плоскостями проекций

Лекция 2. Проекции точки, прямой и
плоскости
28

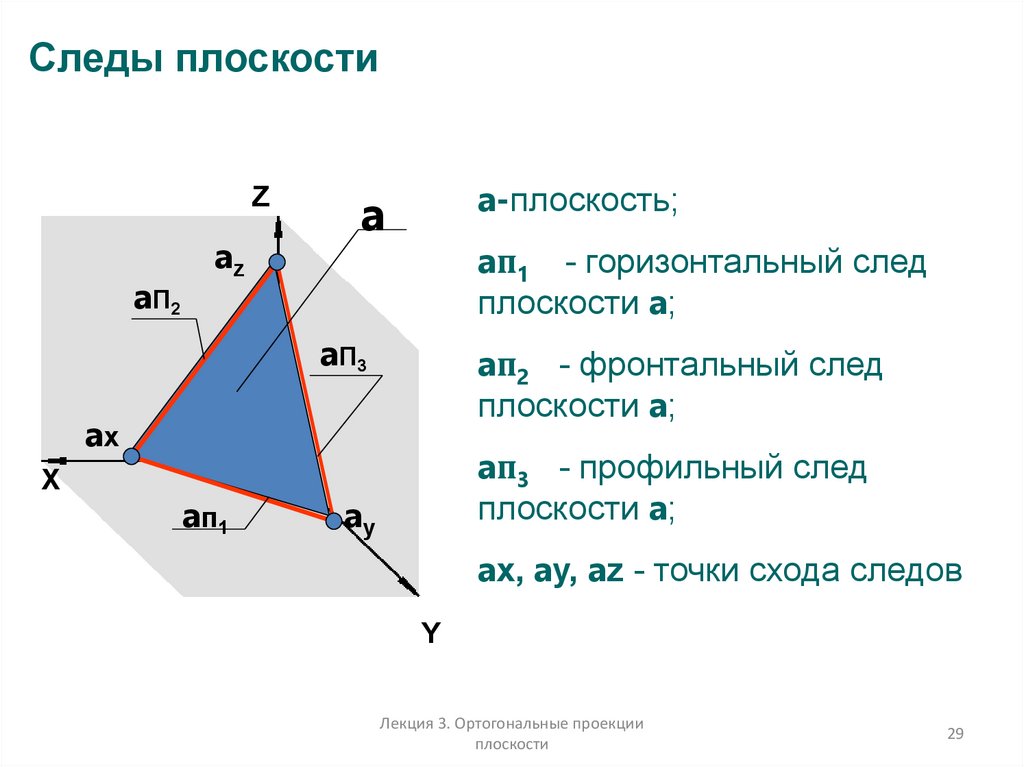
29.

Следы плоскости
Z
a П2
az
a-плоскость;
a
aп1 - горизонтальный след
плоскости a;
a П3
aп2 - фронтальный след
плоскости a;
ax
X
a п1
aп3 - профильный след
плоскости a;
ay
ax, ay, az - точки схода следов
Y
Лекция 3. Ортогональные проекции
плоскости
29

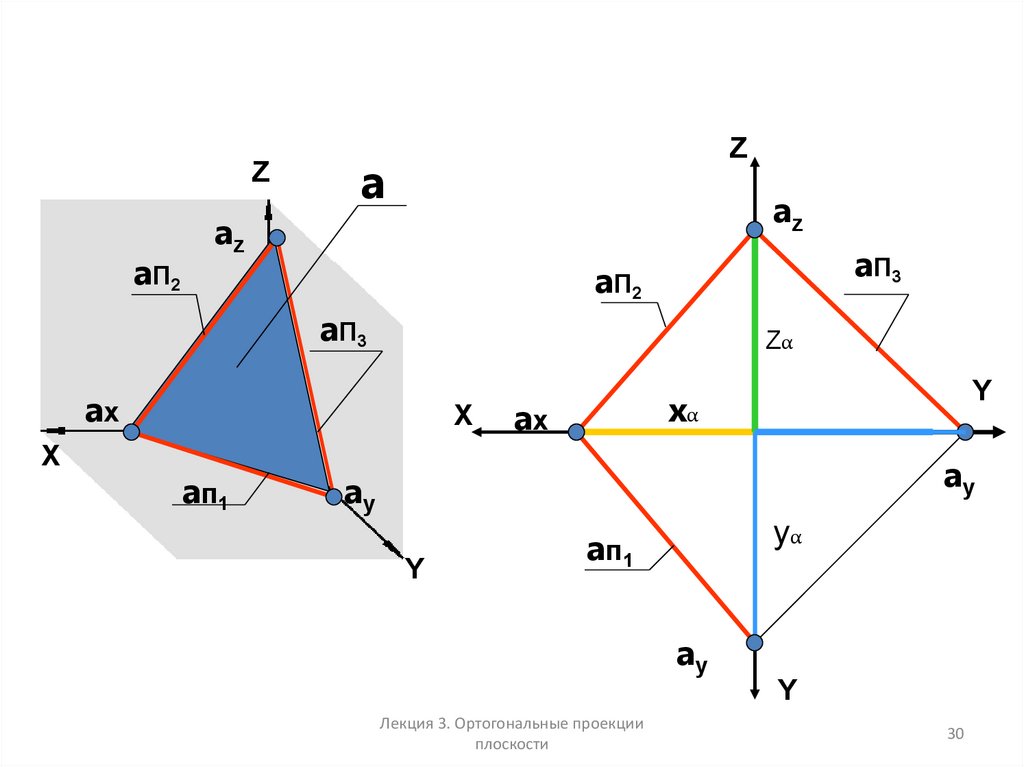
30.

Z
a П2
Z
a
az
az
a П3
a П2
a П3
Zα
ax
X
X
a п1
Y
xα
ax
ay
ay
Y
yα
a п1
ay
Y
Лекция 3. Ортогональные проекции
плоскости
30

31. ПОЛОЖЕНИЕ ПЛОСКОСТЕЙ ОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ

1.
Относительно плоскостей проекций
разделяют:
• плоскости частного положения
• плоскости общего положения
плоскости
2. Плоскости частного положения подразделяют на
• плоскости параллельные плоскостям проекций –
плоскости уровня
• плоскости перпендикулярные плоскостям проекций –
плоскости проецирующие
Лекция 2. Проекция прямой линии и
плоскости
31

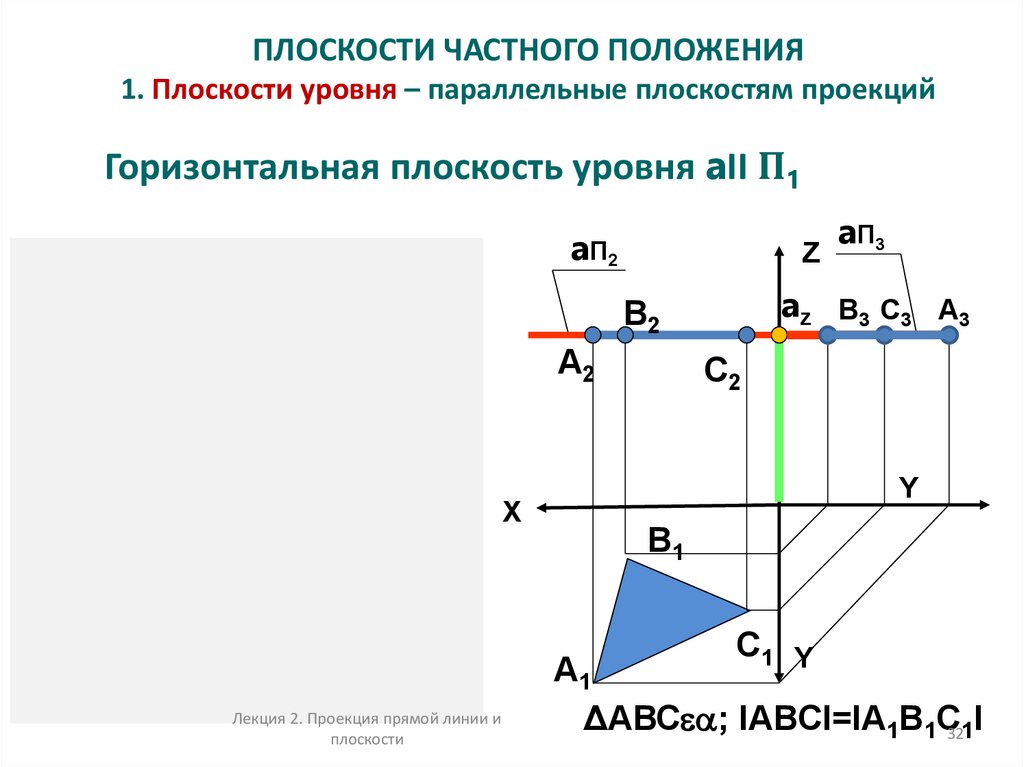
32. ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ 1. Плоскости уровня – параллельные плоскостям проекций

Горизонтальная плоскость уровня aII П1
a П2
a
Z
В2 С az
2
А2
aП2
a П3
А2
В1
А1
С1
Y
Лекция 2. Проекция прямой линии и
плоскости
a П3
az В3 С3 А3
В2
X
X
Z
С2
Y
В1
С1 Y
А1
ΔАВС ; IABCI=IA1B1C321I

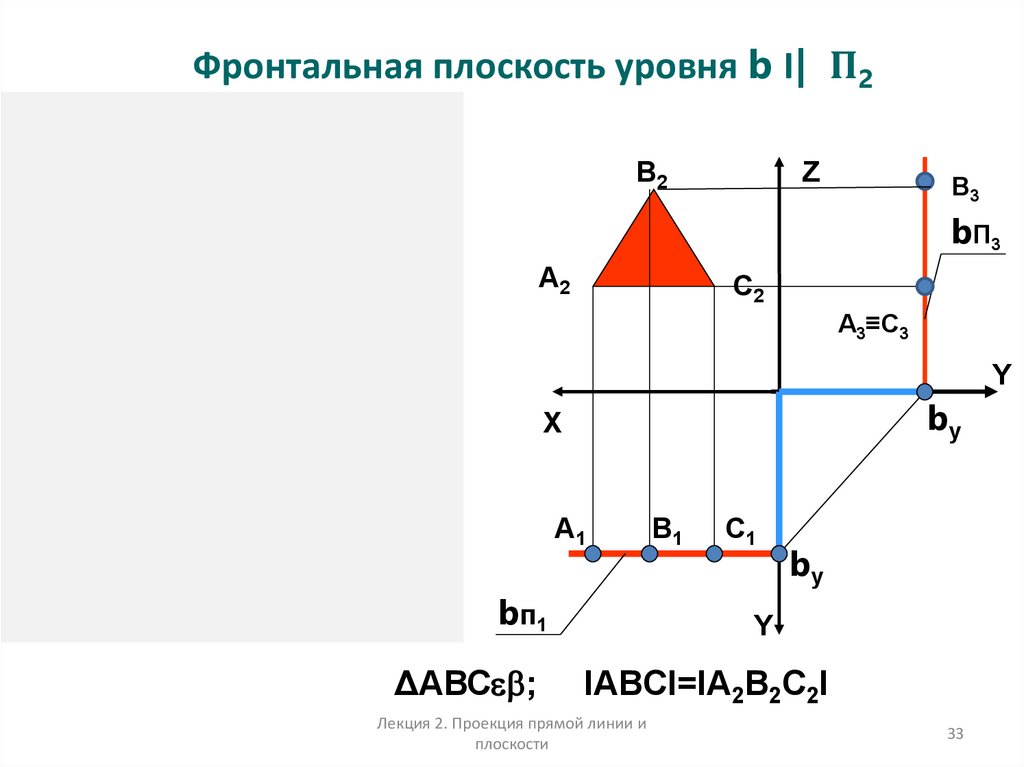
33.

Фронтальная плоскость уровня b I| П2
Z
b
В2
Z
В3
bП 3
А2
С2
bП 3
А3≡С3
Y
X
bп1
by
X
by
А1
Y
bп1
ΔАВС ;
В1
С1
by
Y
IABCI=IA2B2C2I
Лекция 2. Проекция прямой линии и
плоскости
33

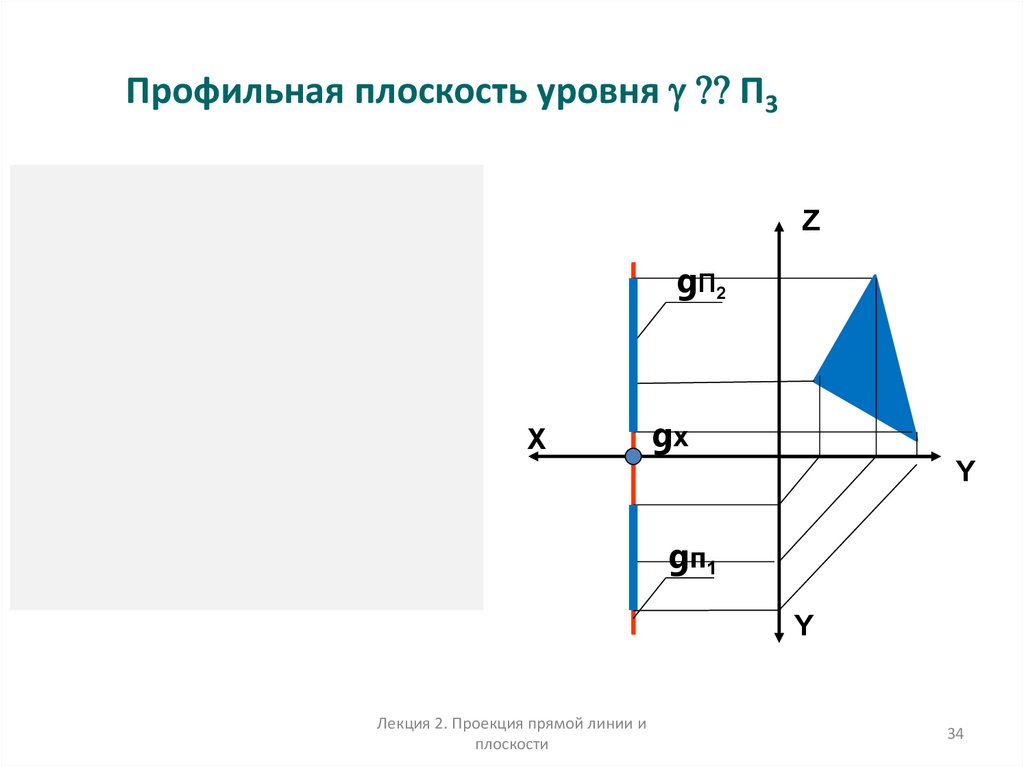
34.

Профильная плоскость уровня П3
Z
g
Z
g П2
g П2
X gx
X
gx
Y
g п1
Y
g п1
Y
Лекция 2. Проекция прямой линии и
плоскости
34

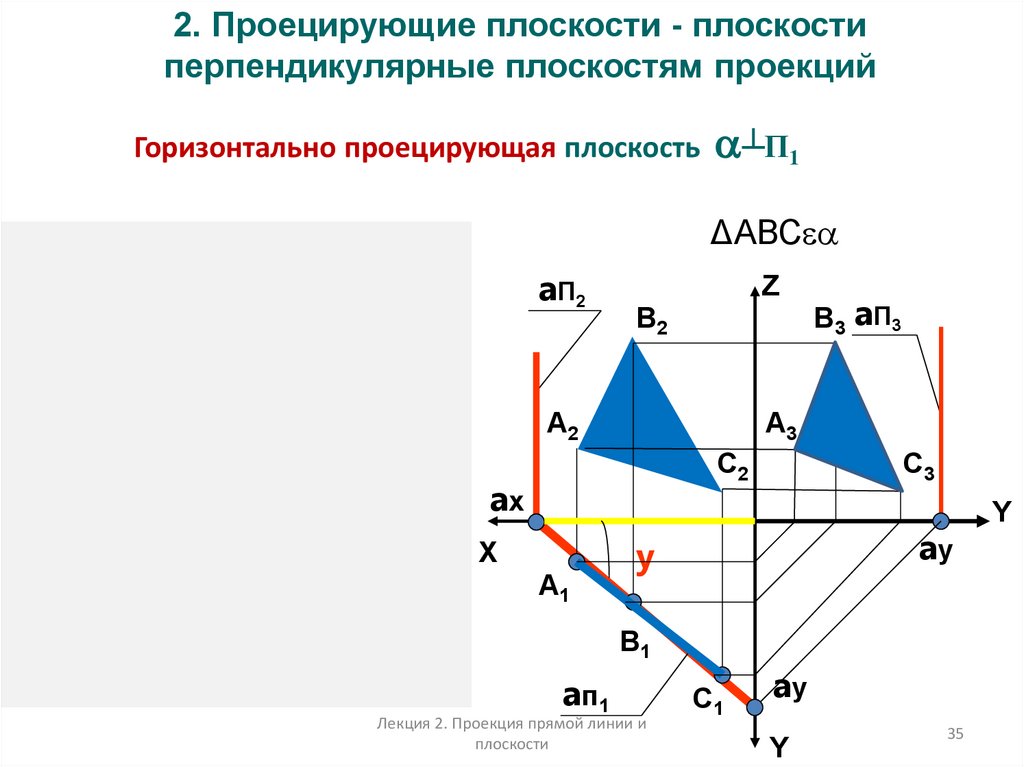
35.

2. Проецирующие плоскости - плоскости
перпендикулярные плоскостям проекций
Горизонтально проецирующая плоскость
┴П1
ΔАВС
Z
a П2
a П2
a
Z
В2
А2
X
a П3
ax
a п1
А3
С2
ax
X
ay
А1
В 3 a П3
С3
ay
y
В1
Y
a п1
Лекция 2. Проекция прямой линии и
плоскости
С1
ay
Y
35
Y

36.

Фронтально проецирующая плоскость ┴ П2
ΔАВС
Z
П2
Z
z
П2
z
С2
В2
П3
x
А2
X
x
X
С3
В3
f
А3
С1
П1
А1
Y
п1
П3
В1
Y
Y

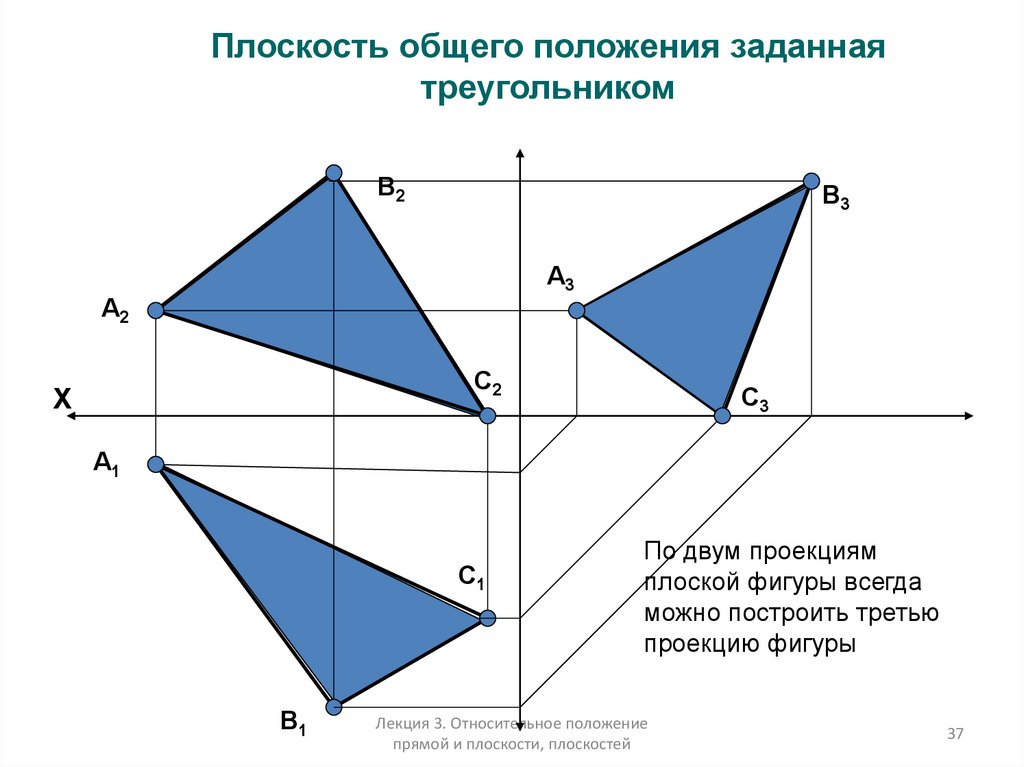
37.

Плоскость общего положения заданная
треугольником
В2
В3
А3
А2
С2
X
С3
А1
С1
В1
По двум проекциям
плоской фигуры всегда
можно построить третью
проекцию фигуры
Лекция 3. Относительное положение
прямой и плоскости, плоскостей
37

38.

ПРИНАДЛЕЖНОСТЬ ТОЧКИ И ПРЯМОЙ
ПЛОСКОСТИ
Точка принадлежит плоскости, если она
принадлежит любой прямой в этой плоскости
Прямая принадлежит плоскости если она проходит:
а) через две точки этой плоскости
б) через точку плоскости параллельно какой-либо
прямой этой плоскости
Лекция 2. Проекция прямой линии и
плоскости
38

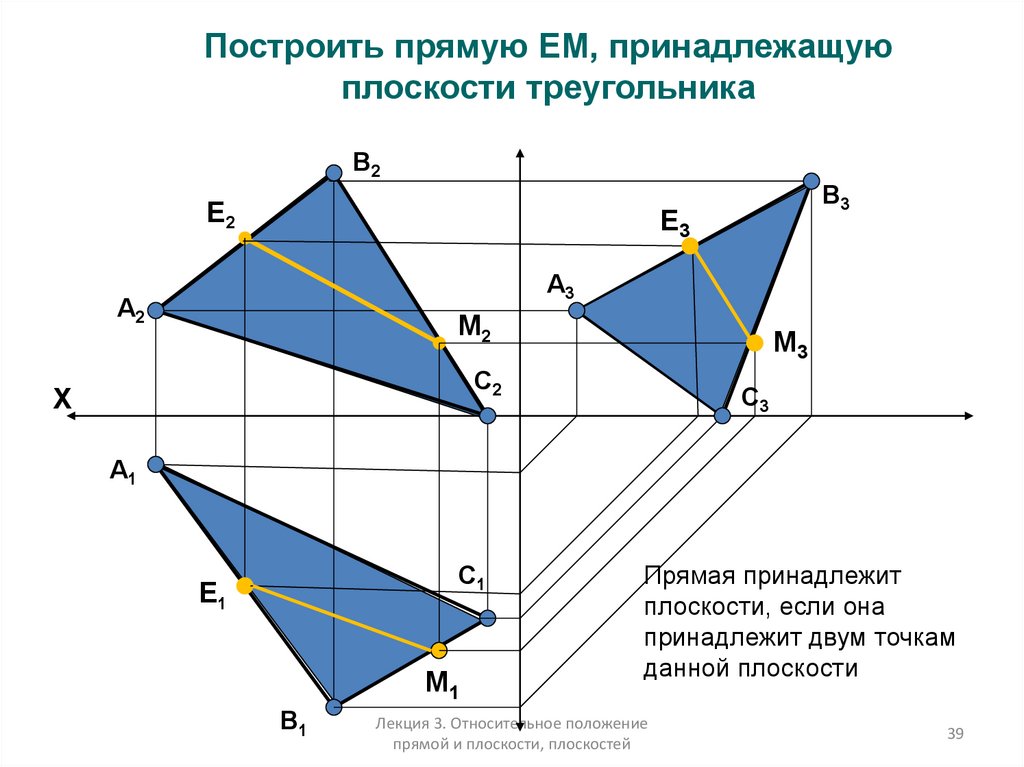
39.

Построить прямую ЕМ, принадлежащую
плоскости треугольника
В2
Е2
В3
Е3
А3
А2
М2
М3
С2
X
С3
А1
С1
Е1
М1
В1
Прямая принадлежит
плоскости, если она
принадлежит двум точкам
данной плоскости
Лекция 3. Относительное положение
прямой и плоскости, плоскостей
39

40. Выводы по теме

• Для создания чертежа (эпюра) применяют
ортогональное (прямоугольное) проецирование
на три плоскости проекций: горизонтальную – П1,
фронтальную – П2, профильную – П3
• Эпюр точки можно построить по координатам,
например А (x, y, z) или по проекциям точки
• Через две точки можно провести прямую линию
• Множество положений прямой линии образуют
плоскость
Лекция 2. Проекции точки, прямой и
плоскости
40

41. Выводы по теме

• Прямые и плоскости подразделяются на прямые и
плоскости общего и частного положения
относительно плоскостей проекций
• Прямые и плоскости частного положения либо
перпендикулярны, либо параллельны плоскостям
проекций
• Прямые и плоскости общего положения не
параллельны и не перпендикулярны плоскостям
проекций
• Прямая линия принадлежит плоскости, если она
принадлежит двум точкам данной плоскости
Лекция 2. Проекции точки, прямой и
плоскости
41

42. Список рекомендуемой литературы

• Королев Ю. И. Начертательная геометрия: учебник
для студентов вузов, обучающихся по направлениям
подгот. бакалавров, магистров и дипломир.
специалистов по курсу "Начертат. геометрия" в техн.
вузах / Ю. И. Королев. - Москва ; Санкт-Петербург ;
Нижний Новгород [и др.]: Питер, 2007. - 252 с.:
• Нартова Л. Г. Начертательная геометрия. Теория и
практика: учеб. для студентов вузов, обучающихся по
направлениям подгот. и специальностям в обл.
техники и технологии / Л. Г. Нартова, В. И. Якунин. Москва: Дрофа, 2008. – 302 с.
Лекция 2. Проекция прямой линии и
плоскости
42

43. Список рекомендуемой литературы

• Бударин О. С. Начертательная геометрия. Краткий
курс: учеб. пособие для студентов вузов,
обучающихся по направлениям в обл. техники и
технологий / О. С. Бударин. - 2-е изд., испр. Санкт-Петербург ; Москва ; Краснодар: Лань,
2009. - 368 с.
• Чекмарев А. А. Начертательная геометрия и
черчение: учеб. для студентов вузов,
обучающихся по техн. специальностям / А. А.
Чекмарев. - 3-е изд., перераб. и доп. - Москва:
Юрайт, 2011. - 471 с.:
Лекция 2. Проекции точки, прямой и
плоскости
43

44. Благодарю за внимание

Лекция 2. Проекции точки, прямой и
плоскости
44