Похожие презентации:
Модели авторегрессии АР(р), авторегрессии скользящего среднего СС(q). Лекция 4 (часть 3)
1. Лекция 4 (часть 3)
Модели авторегрессии АР(р),авторегрессии скользящего
среднего СС(q)
2. Цель лекции
Цель лекции - формирование теоретическихзнаний о моделях стационарных временных рядов
позволяющих
прогнозировать
соиальноэкономические
явления
и
процессы
на
краткосрочную
перспективу,
а
также
формирование навыков реализации указанных
моделей и методов в пакетах прикладных
программ
2
3. План лекции
1.Общий вид модели авторегрессии. Условие стационарности
процесса авторегрессии
2.
Свойства процесса АР
3.
Оценивание параметров модели АР
4.
Прогнозирование по модели АР
5.
Смешанные модели АРСС: идентификация и прогнозирования
6.
Информационные критерии
3
4. Реализуемые компетенции
ОПК-1 готовностью к самостоятельной работеОПК-2 способностью использовать современные математические методы и
современные прикладные программные средства и осваивать современные технологии
программирования
ПК-1 способностью использовать стандартные пакеты прикладных программ для
решения практических задач на электронных вычислительных машинах, отлаживать,
тестировать прикладное программное обеспечение
ПК-9 способностью выявить естественнонаучную сущность проблем, возникающих в
ходе профессиональной деятельности, готовностью использовать для их решения
соответствующий естественнонаучный аппарат
ПК-10 готовностью применять математический аппарат для решения поставленных
задач, способностью применить соответствующую процессу математическую модель и
проверить ее адекватность, провести анализ результатов моделирования, принять
решение на основе полученных результатов
ПК-11 готовностью применять знания и навыки управления информацией
ПК-12 способностью самостоятельно изучать новые разделы фундаментальных наук
4
5. Общий вид модели авторегрессии. Условие стационарности процесса авторегрессии
Вернемся к выражению, где показано, что при выполнении условияобратимости процесс скользящего среднего принимает вид:
t c0 c1 L c2 L2 ... ck Lk ... t .
(1)
Если выразить t через все его предыдущие значения и t , то
получим:
с
с0
с
с0
с
с0
t 1 t 1 2 t 2 .... k t k ...
1
t
с0
(2)
Введя новые обозначения, получаем:
t 1 t 1 2 t 2 ... k t k ... t
(3)
Этот процесс по построению является стационарным.
5
6. Общий вид модели авторегрессии. Условие стационарности процесса авторегрессии
Определение Процесс, значения которого определяются линейнойкомбинацией конечного числа его предыдущих значений и добавлением
белого шума, называется процессом авторегрессии порядка p (АР(p),
AR(p)).
Общий вид модели:
АР(p): t 1 t 1 2 t 2 .... p t p t
(4)
t=p+1,…,N.
Как правило, рассматривают модели невысокого порядка.
Модель авторегрессии первого порядка обозначается АР(1) и
записывается как:
t 1 t 1 t
(5)
АР(1) зачастую называют марковским процессом ( 1 1)).
Модель авторегрессии второго порядка называют процессом Юла.
АР(2): t 1 t 1 2 t 2 t (процесс Юла)
(6)
6
7. Общий вид модели авторегрессии. Условие стационарности процесса авторегрессии
Запишем уравнение процесса, используя оператор сдвига:t 1 t 1 2 t 2 .... р t р t
1 L L ... L
2
1
2
p L t t
(7)
p
p
t
t
(8)
(9)
Получили разностное уравнение относительно со случайной
правой частью t , общее решение которого складывается из общего решения
однородного уравнения (без t , в правой части нуль) и частного решения
неоднородного уравнения.
7
8. Общий вид модели авторегрессии. Условие стационарности процесса авторегрессии
Общее решение однородного уравнения имеет вид:p
t Ci t i t ,
(10)
i 1
где i - различные по величине корни характеристического уравнения,
p 1 P 1 2 p 2 .... p 0
(11)
Ci t - полиномы, степень которых на единицу меньше кратности
соответствующего корня.
Решение однородного уравнения будет устойчиво (не будет уходить в
бесконечность), если i 1, i 1,.., p . Как показано выше, в этом случае
существует обратный оператор p L и имеет смысл выражение
1
t
1
,
p L t
(12)
то есть процесс t принимает вид, соответствующий теореме Вольда.
Если все корни характеристического уравнения 1 , 2 ,..., р по модулю
строго меньше единицы (лежат внутри единичного круга), процесс АР(p)
является стационарным. Это условие является необходимым и достаточным.
8
9. 2 Свойства процесса авторегрессии
Найти математическое ожидание процесса авторегрессии для рядадинамики с нулевым средним.
Записать процесс авторегрессии первого порядка в последовательно
подставляя значения t i
Найти дисперсию.
9
10. 2 Свойства процесса авторегрессии
Найдем математическое ожидание процесса авторегрессии для рядадинамики с нулевым средним:
M ( t ) M ( t 1 t 1 2 t 2 .... p t p ) 0
(13)
Следует отметить, что математическое ожидание будет равно 0 , в
случае не центрированных данных.
Запишем процесс авторегрессии первого порядка в следующем виде:
N 1
t 1 t 1 t = t 2 1 t 1 t ... 1 1i t i
2
1
N
1
(14)
i 0
Найдем дисперсию:
2
D( t ) D( 1 )
1 12
i 0
i 0
N 1
N
1
N 1
i
1 t i
2
2i
1
(15)
10
11. 2 Свойства процесса авторегрессии
Найдем дисперсию процесса авторегрессии порядка р:Воспользуемся выражением:
t
1
p L
t
1
2
D( t ) D(
t )
1 1 L 2 L2 ... p Lp
(1 1 L 2 L2 ... p Lp ) 2
(16)
(17)
Найдем автоковариационную функцию:
Умножим авторегрессию порядка р на t и возьмем математическое
ожидание:
M t t 1 M t 1 t 2 M t 2 t .... p M t p t M t t
(18)
11
12. 2 Свойства процесса авторегрессии
При выполнении условия стационарности t можно выразить каклинейную комбинацию белых шумов t , t 1, t 2, ... . Следовательно,
M t t 0 . Так как ряд t
центрирован, то переходя к обозначению
автоковариации получаем:
1 1 2 2 .... p р
(19)
Учтем, четность автоковариации стационарного ряда:
1 1 и 1 p p 1 .
12
13. 2 Свойства процесса авторегрессии
Тогда элементы автоковариационной функции процесса авторегрессиипорядка p для разных :
(1) 1 0 2 1 3 2 .... p p 1
(
2
)
1
0
1
....
p
2
1
2
3
p
...
p p 1 p 2 p 3 .... 0
1
2
3
p
Запишем
автокорреляционную
функцию
для
АР(р),
(20)
разделив
автоковариации на дисперсию 0 :
1 1 2 2 .... p p
(21)
для 1, 2,..., p получаем:
(1) 1 2 1 3 2 .... p p 1
(
2
)
1
1
....
p
2
1
2
3
p
...
p p 1 p 2 p 3 ....
1
2
3
p
(22)
13
14. 2 Свойства процесса авторегрессии
элементы автокорреляционной функции через ( )( ( ) ( (1), (2)... ( р))Т ). Запишем выражение (2.147) в векторно-матричной
форме:
( ) R ,
(23)
Обозначим
1
где 2 - вектор параметров авторегрессии,
...
p
R - корреляционная матрица размерности р*р:
(1)
(2)
1
1
(1)
(1)
R (2)
(1)
1
рxр
...
...
...
( р 1) ( р 2) ( р 3)
... ( р 1)
... ( р 2)
... ( р 3)
...
...
...
1
(24)
Система (22-23) называется системой Юла-Уокера.
14
15. 2 Свойства процесса авторегрессии
Вернемся к (21)1 1 2 2 .... p p
Элементы автоковариационной функции удовлетворяют разностному
уравнению, совпадающему с однородным уравнением для процесса t .
Можно записать:
p
1 L 0
i
(24)
i 1
Решая это разностное уравнение, можно получить общий вид АКФ для
авторегрессии.
Общее решение этого уравнения (для случая разных корней) имеет вид:
C1 1 C2 2 ... C p p
(25)
15
16. 2 Свойства процесса авторегрессии
Подставим это выражение в (24):1 L C C ... C C 1 L ... C 1 L
p
i
1 1
2
2
p
i 1
p
1 1
p
i
i 1
j 1 j L 1 i L
i 1,i j
p
1)
p
p
p
i
i 1
(26)
если корень i - вещественный, то C i i геометрически убывает с
ростом (затухающая экспонента)
2)
если корень i - комплексный, то i и j - комплексносопряженные корни, дающие член, который является затухающей
синусоидальной волной.
16
17. 2 Свойства процесса авторегрессии
Запишем элементы автокорреляционной функции для авторегрессиипервого порядка. Система Юла-Уокера в этом случае сводится к одному
уравнению, непосредственно определяющему оценку коэффициента 1= (1) .
(2) 1 (1) 2 (1) и т.д.
Найдем
частную
автокорреляционную
функцию
авторегрессии
порядка p. Напомним, что частный коэффициент автокорреляции порядка р
для процесса t – это коэффициент корреляции между t и t р очищенный
от влияния промежуточных уровней t 1 , t 2 , …, t р 1 .
Известно, что коэффициенты уравнения множественной регрессии
можно вычислить как произведение частного коэффициента корреляции на
отношение корней соответствующих остаточных дисперсий.
17
18. 2 Свойства процесса авторегрессии
Учитывая, что 1, N стационарный ряд с постоянным нулевымматематическим ожиданием и постоянной дисперсией, получаем, что
параметры регрессии равны частным коэффициентам корреляции:
t р1 t 1 р 2 t 2 ... рр t р t ,
(27)
Получаем, что частный коэффициент автокорреляции порядка р –
это коэффициент при последнем регрессоре.
Очевидно, что если
процесс t - это процесс АР(p), то рр р .
Составим систему уравнений Юла-Уокера для р 1 р1 рр T .
Эти уравнения связывают коэффициенты АКФ р 1 1 р T и
ЧАКФ р 1 р1 рр T .
18
19. 2 Свойства процесса авторегрессии
11
2
R p p 3
4
k 1
1
1
1
2
3
k 2
2
1
1
1
2
k 3
3
2
1
1
1
k 4
4
3
2
1
1
k 1
k 2
k 3
k 4 (28)
k 5
1
Решая эту систему для р 1,2,3... , находим частные коэффициенты
автокорреляции 1-го, 2-го, 3-го и т.д. порядков.
Частный коэффициент автокорреляции 1-го порядка:
11 1
Частный коэффициент автокорреляции 2-го порядка.
19
20. 2 Свойства процесса авторегрессии
Нас интересует значение только одного неизвестного параметра всистеме уравнений, в этом случае для нахождения 22 удобнее использовать
правило Крамера:
kk
k
,
(29)
где - определитель матрицы системы, то есть R k k , а k определитель матрицы системы, в которой k -ый столбец заменен на столбец
правой части, то есть k 1 1 k . Получаем:
T
1 1
22
1 2
1 1 2 2 1
1 1
1 2 1
(30)
20
21. 2 Свойства процесса авторегрессии
Частный коэффициент автокорреляции 3-го порядка:1
1 1
33 1 1 2
2 1 3
1
1 2
1 1
1
2 1 1
3 3 1 2 2 1 2 1 3 2 1 2
2
2
2
1 2 1 2 2 1 2
(31)
3 3 1 2 2 1 2 1 3 2 1 2
1 2 2 2 2 1 1 2
3 3 1 2 2 1 2 1 3 2 1 2
1 2 2 2 1 1 2
и т.д.
21
22. 2 Свойства процесса авторегрессии
Рассмотрим частную автокорреляционную функцию для авторегрессиипервого порядка.
11 1
2 2 1
22
1 2 1
(32)
Учитывая, что (1) 1 , (2) 12
Получаем, что
12 1 2
22
0
2
1 1
(33)
22
23. 3 Оценивание параметров модели авторегрессии
Оценивание параметров моделей авторегрессии можно производить:1. Методом максимального правдоподобия.
2. Методом, на основе системы Юла-Уокера.
3. Методом наименьших квадратов.
Рассмотрим метод, основанный на соотношениях Юла-Уокера.
Так как матрица R невырождена, то умножив (23) на R 1 получим:
R 1 ( ) .
(34)
Подставляя в это выражение значения соответствующих параметров
получаем:
ˆ Rˆ 1rˆ( ) .
(35)
23
24. 3 Оценивание параметров модели авторегрессии
Рассмотрим метод наименьших квадратов для оценивания параметровмодели
авторегрессии.
Оценка
параметров
модели
авторегрессии
производится по формуле:
ˆ ( X T X ) 1 X T Y ,
(36)
1 y p ... y1
1
y
y
p 1
2
Х
N *( p 1)
...
1 y
... y N p
N 1
(37)
y p 1
y
Y p 2 .
( N p )*1
...
y
N
(38)
где Х реализация матрицы :
МНК рекомендуется применять только при больших N.
24
25. 4 Прогнозирование по модели авторегрессии
Прогнозирование по модели АР(р) осуществляется путемподстановки предшествующих значений временного ряда.
Пусть оценка модели авторегрессии порядка р имеет вид:
yt ˆ1 yt 1 ˆ 2 yt 2 ... ˆ p yt p
(39)
Прогноз на 1 шаг вперед находим как:
y N 1 ˆ1 y N ˆ 2 y N 1 ... ˆ p y N p 1
(40)
На 2 шага вперед
yˆ N 2 ˆ1 yˆ N 1 ˆ 2 y N ... ˆ p y N p 2
(41)
и т.д.
yˆ N p 1 ˆ1 yˆ N p ˆ 2 yˆ N p 1 ... ˆ p yˆ N 1
(42)
Таким образом, для каждого последующего прогноза в оценку
модели подставляются прогнозные значения предшествующих периодов,
таким образом, теоретически прогнозирование может продолжаться
бесконечно, по этой причине модель авторегрессии называют моделью с
бесконечной памятью.
25
26. 4 Прогнозирование по модели авторегрессии
Интервальный прогнозДисперсия ошибки прогноза на 1 шаг вперед:
D N 1 ˆ N 1 D N 1 1 N 1 N D N 1 2
(43)
Дисперсия ошибки прогноза на 2 шага вперед:
D N 2 ˆ N 2 D N 2 1 N 1 1 ˆ N 1 D N 2 1 ( 1 N N 1 ) 1 1 N
D N 2 1 N 1 (1 )
2
1
2
(44)
На три шага:
D N 3 ˆ N 3 D N 3 1 N 2 1 ˆ N 2 D N 3 1 ( 1 N 1 N 2 ) 1 1 N 1
D N 3 1 ( 1 ( 1 N N 1 ) N 2 ) N D N 3 1 N 2 N 1 (1 )
3
1
2
1
2
1
4
1
2
(45)
и т.д.
26
27. 4 Прогнозирование по модели авторегрессии
Для модели АР(р) дисперсия ошибки прогноза на один шаг:D N 1 ˆ N 1 D N 1 1 N 2 N 1 ... p N p 1 1 N 2 N 1 ... p N p
D N 1
на два шага:
2
D N 2 ˆ N 2 D N 2 1 ( 1 N ... p N p N 1 ) 2 N ... p N p 2
( 1 ( 1 N ... p N p ) ... p N p 2 ) D N 2 1 N 1 (1 )
2
1
2
(46)
(47)
И т.д. по аналогии с предыдущим примером.
При прогнозировании дисперсия прогноза постоянно возрастает.
Если остатки модели АР(р) – нормальный белый шум, то доверительный
интервал строится аналогично как и в моделях скользящего среднего.
27
28. 5 Смешанные модели: АРСС(p,q)
Двойственность процессов АР и СС заключается в том, что1) при выполнении условия обратимости конечный процесс СС (q)
может быть представлен в виде бесконечного процесса AR ;
2) при выполнении условия стационарности конечный процесс АР(p)
может быть представлен в виде бесконечного процесса CC .
По этой причине есть смысл вместо, допустим модели авторегрессии
высокого порядка, искать адекватную модель скользящего среднего более
низкого порядка, и наоборот.
28
29. 5 Смешанные модели: АРСС(p,q)
Перейдем к комбинации процессов АР и СС – процессам АРСС(p,q)(ARMA), то есть рассмотрим смешанную модель:
t 1 t 1 2 t 2 .... p t p t 1 t 1 2 t 2 .... q t q
(48)
Или в операторной записи: p L t q L t
(49)
Условия стационарности процесса АРСС
1)
Если все корни полинома p L по модулю меньше 1, то
существует обратный оператор и можно записать:
t p L 1 q L t .
(50)
Вывод: стационарность процесса АРСС определяется только его АРчастью.
2)
Если все корни полинома q L по модулю меньше 1, то
существует обратный оператор и можно записать:
t q L 1 p L t .
(51)
Таким образом обратимость процесса АРСС определяется только его
СС-частью.
29
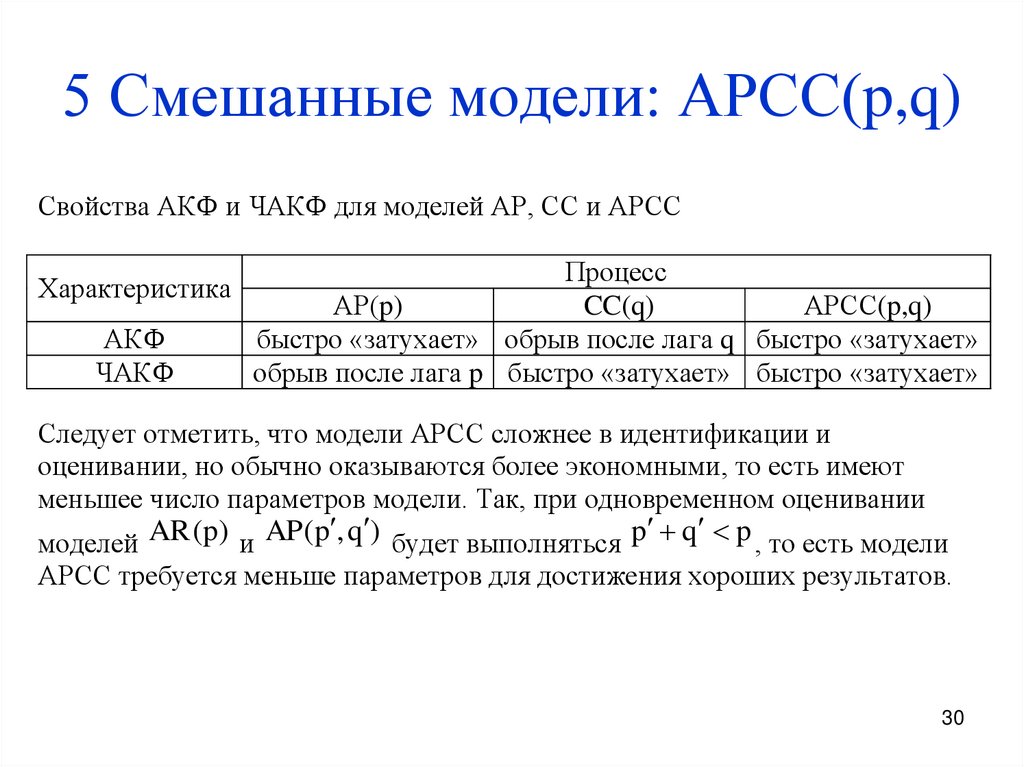
30. 5 Смешанные модели: АРСС(p,q)
Свойства АКФ и ЧАКФ для моделей АР, СС и АРССХарактеристика
АКФ
ЧАКФ
Процесс
АР(p)
CC(q)
АРСС(p,q)
быстро «затухает» обрыв после лага q быстро «затухает»
обрыв после лага p быстро «затухает» быстро «затухает»
Следует отметить, что модели АРСС сложнее в идентификации и
оценивании, но обычно оказываются более экономными, то есть имеют
меньшее число параметров модели. Так, при одновременном оценивании
моделей AR (p) и AP(p , q ) будет выполняться p q p , то есть модели
АРСС требуется меньше параметров для достижения хороших результатов.
30
31. 5 Смешанные модели: АРСС(p,q)
Оценивание параметров модели АРСС рассмотрим на примере моделиАРСС(2,2).
В операторной записи 2 L t 2 L t
Выразим t
(1 1L 2 L2 ) t
t
.
1 1L 2 L2
(52)
t
.
2
1 1L 2 L
(53)
Обозначим
t
Получили выражение связывающее t и t .
t (1 1L 2L2 ) t ,
Фактически перед нами модель СС(2), где роль t играет t .
(54)
31
32. 5 Смешанные модели: АРСС(p,q)
Найдем значения t (обозначим их z) через наблюденные значения t :Z1 у1 , Z2 у 2 1Z1 .
(55)
При этом величину 1 назначим так, чтоб выполнялось условие обратимости
(например, 0,5, а по условию обратимости по модулю меньше 1).
Z3 у3 1Z2 2 Z1
(56)
2 назначим тех же соображений. И так далее, ищут все значения Z.
Запишем выражение:
t 1 t 1 1 t 2 t .
(57)
В обозначениях t перед нами модель AR(2).
Значения t мы нашли, назначив 1 , 2 , найдем неизвестные параметры
1 , 2 методом наименьших квадратов. После каждого назначения пар 1 , 2 и
последующего нахождения 1 , 2 методом наименьших квадратов
рассчитывают суммы квадратов отклонений модельных значений от
наблюденных (остаточная дисперсия). Тот набор параметров, который
обеспечит минимум остаточной дисперсии и будет искомым набором.
32
33. 5 Смешанные модели: АРСС(p,q)
Прогнозирование по модели АРСС.yt ˆ1 yt 1 ˆ 2 yt 2 1 zt 1 2 zt 2
(58)
Прогноз на 1 шаг вперед находим как:
y N 1 ˆ1 y N ˆ 2 y N 1 ˆ1 z N ˆ2 z N 1
(59)
На 2 шага вперед
yˆ N 2 ˆ1 yˆ N 1 ˆ 2 y N ˆ1 * 0 ˆ2 z N
(60)
На 3 шага
yˆ 3 ˆ1 yˆ N 3 ˆ 2 yˆ N 1
(61)
Таким образом, прогноз дальше идет только по АР части.
33
34. Смешанные модели агрегированных рядов
Гренжером и Моррисом доказана теорема о возможности появлениясмешанных моделей в результате агрегирования рядов со сравнительно
простой структурой.
Теорема:
Пусть 1, N и 1, N - два независимых стационарных ряда с нулевым
математическим ожиданием.
Тогда если t ~ АРСС(p1,m), t ~ АРСС(p2,n) и t t t ,
то t ~ АРСС (r,s) : r p1 p 2 и s max p1 n, p 2 m .
Особый интерес представляют два случая агрегирования:
а) ряды агрегируются и образуют один общий (большинство
макроэкономических рядов – ВВП, экспорт, импорт и т.д.)
б) наблюденный ряд
- сумма истинного процесса и ошибки
наблюдения (практически любой макроэкономический ряд).
34
35. Смешанные модели агрегированных рядов
например, авторегрессионный процесс наблюдается в присутствиибелого шума:
AP ( p) +АР(0) = APCC (r, s)
APCC(p,0) APCC(0,0) APCC p, p
r p 0 , s max p 0,0 0 p
Таким образом, меняется тип модели.
Пусть процесс СС наблюдается в присутствии белого шума:
CC q +СС(0)= CC q
APCC 0, q APCC 0,0 APCC(0, q) CC(q)
Мы видим, что не меняется тип и порядок модели
35
36. 6 Информационные критерии выбора модели
для сравнения и выбора лучшей модели используются так называемыеинформационные критерии – Акаике (AIC), байесовский критерий Шварца
(BIC) и Хеннана-Куинна (HQ):
AIC ln S ост 2
2
p q
,
N
pN q ln N ,
BIC ln S ост
2
pN q ln(ln N )
HQ ln S ост
2
где S 2 ост – оценка остаточной дисперсии;
p, q – количество оцениваемых параметров АР и СС;
N – длина временного ряда.
36
37. Задание на практическое занятие
1. Записать АКФ и ЧАКФ для АР(2)2. Показать какие ограничения
накладываются на значения параметров
модели авторегрессии второго порядка
37
38. Задание на лабораторную работу
По методичке• На основе данных об индексах основных
социально-экономических показателях РФ,
представленных на сайтах gks.ru, sophist.hse.ru:
• - исследовать компонентный состав ряда
динамики на основе непараметрических
критериев;
• - осуществить прогнозирование по методу,
соответствующему компонентному составу
временного ряда.
38
39. Литература к лекции
Канторович, Г. Г. Анализ временных рядов//
Экономический журнал ВШЭ– 2002 г. – №1, с.85-116.
Чураков Е.П. Математические методы обработки
экспериментальных данных в экономике: Учеб.пособие.
– М.: Финансы и статистика, 2004.
Чураков Е.П. Прогнозирование эконометрических
временных рядов: Учебное пособие -М.: Фин. и стат.,
2008.(Заказ-2008).
Лукашин, Ю. П. Адаптивные методы
краткосрочного прогнозирования временных
рядов [Текст] : учеб. пособие для вузов / Ю. П.
Лукашин. - М. : Финансы и статистика, 2003. - 416 с.
39






































 Математика
Математика








