Похожие презентации:
Линейные модели (линейная и логистическая регрессия)
1.
Линейные модели (линейнаяи логистическая регрессия)
2.
Математический оффтоп (вектор)3.
Математический оффтоп (матрица)4.
Математический оффтоп (матрица транспонированная)5.
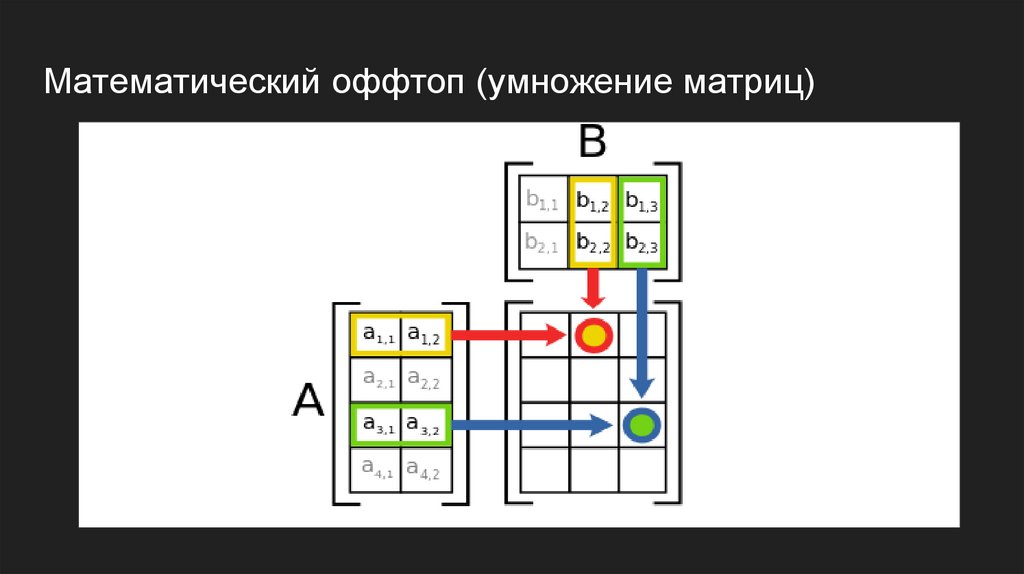
Математический оффтоп (умножение матриц)6.
Математический оффтоп (умножение матриц)7.
Произведение матрицы на вектор8.
Обратная матрица9.
L1 и L2 норма10.
L1 и L2 норма11.
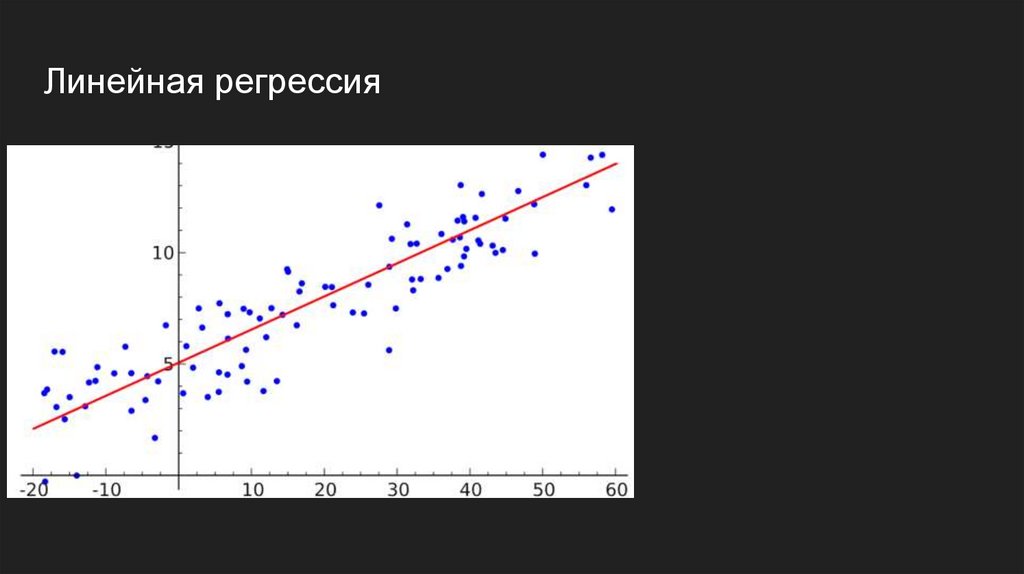
Линейная регрессия12.
Вспомним постановку задачи-
X - множество параметров
Y - множество ответов
Наша задача - построить такую f: X -> Y, причем f должна быть
наилучшей с …
13.
Линейная регрессия14.
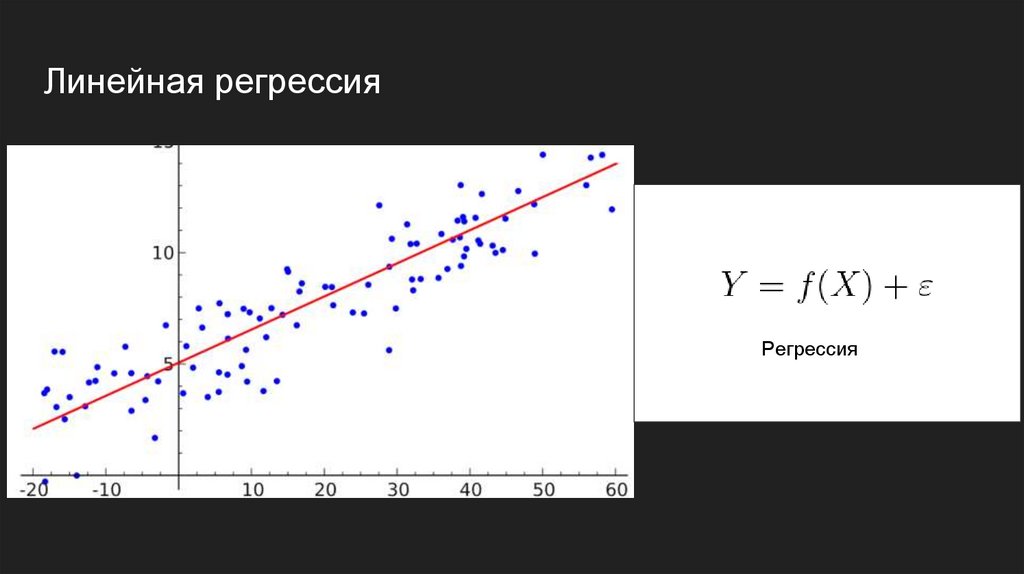
Линейная регрессияРегрессия
15.
Линейная регрессия16.
Линейная регрессия17.
Линейная регрессия18.
Линейная регрессия19.
Линейная регрессия20.
Линейная регрессияМинимизируем W (вектор весов)
21.
Линейная регрессияМинимизируем W (вектор весов)
22.
Линейная регрессия23.
Линейная регрессия24.
Линейная регрессия25.
Линейная регрессия26.
Линейная регрессия27.
Линейная регрессия28.
Линейная регрессия29.
Линейная регрессия-
Но(!) у нас есть обратная матрица, а матрицы не всегда обратимы
Например, если у нас есть сильно скоррелированные фичи
30.
Линейная регрессия-
Но(!) у нас есть обратная матрица, а матрицы не всегда обратимы
Например, если у нас есть сильно скоррелированные фичи
31.
Линейная регрессия-
Но(!) у нас есть обратная матрица, а матрицы не всегда обратимы
Например, если у нас есть сильно скоррелированные фичи
32.
Регуляризация33.
Регуляризация34.
Регуляризация35.
Регуляризация36.
Метрики-
MSE
37.
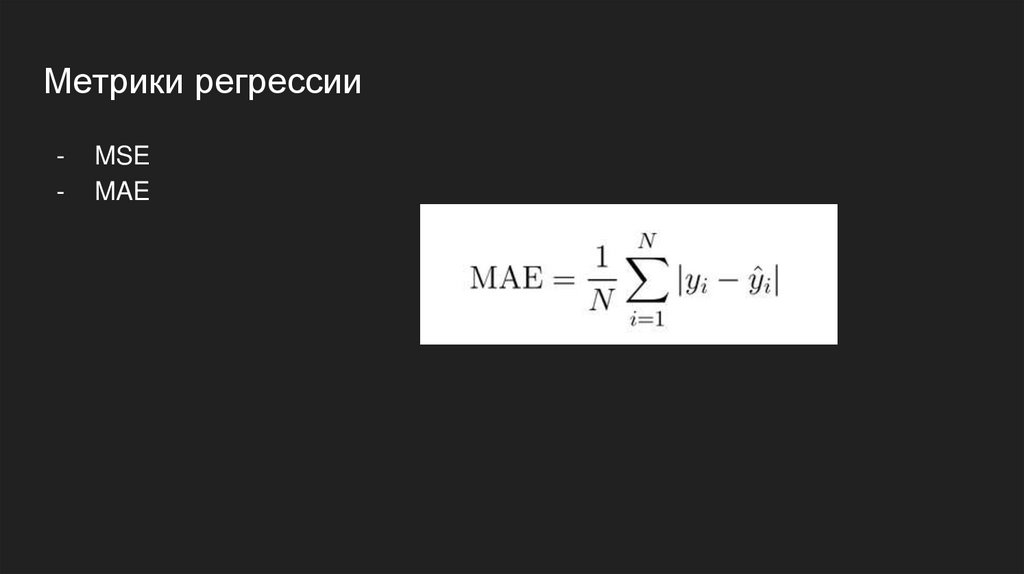
Метрики регрессии-
MSE
MAE
38.
Метрики регрессии-
MSE
MAE
RMSE
39.
Метрики регрессии-
MSE
MAE
RMSE
MAPE
40.
Метрики регрессии-
MSE
MAE
RMSE
MAPE
R2
41.
Логистическая регрессия42.
Логистическая регрессия43.
Логистическая регрессия44.
Логистическая регрессия45.
Логистическая регрессия46.
Логистическая регрессия-
Для начала разберемся с бинарной классификацией, те С = {-1, 1}
47.
Логистическая регрессия-
Для начала разберемся с бинарной классификацией, те С = {-1, 1}
Как используя модель для линейной регрессии, решить задачу бинарной
классификации?
48.
Логистическая регрессия-
Для начала разберемся с бинарной классификацией, те С = {-1, 1}
Как используя модель для линейной регрессии, решить задачу бинарной
классификации?
Выбрать границу и сравнивать с ней (например с 0(?))
49.
Логистическая регрессия-
Для начала разберемся с бинарной классификацией, те С = {-1, 1}
Как используя модель для линейной регрессии, решить задачу бинарной
классификации?
Выбрать границу и сравнивать с ней (например с 0(?))
f(x) = sign(xTw)
50.
Логистическая регрессия51.
Логистическая регрессия (отступ)52.
Логистическая регрессия (отступ)Если отступ положительный - мы
угадали. Отрицательный не
угадали
53.
Логистическая регрессия54.
Логистическая регрессия1. Такой Loss не гладкий
2. Ничего не знаем про уверенность
55.
Логистическая регрессия1. Такой Loss не гладкий
2. Ничего не знаем про уверенность
56.
Логистическая регрессия57.
58.
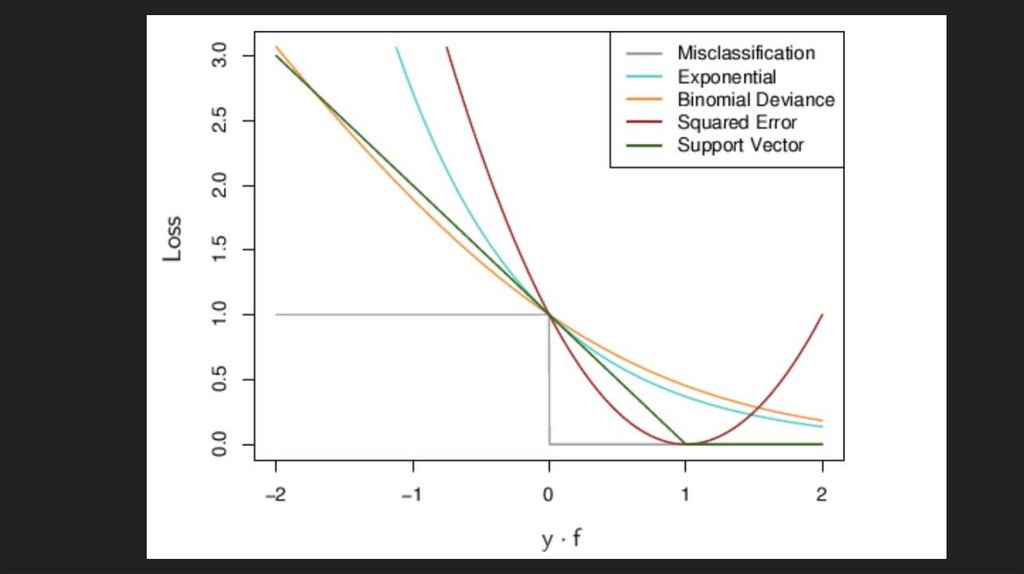
Логистическая регрессия (функции потерь)-
Q(M) = (1 - M)^2
V(M) = (1 - M)_+
E(M) = e^{-M}
L(M) = log(1 + exp(-M))
59.
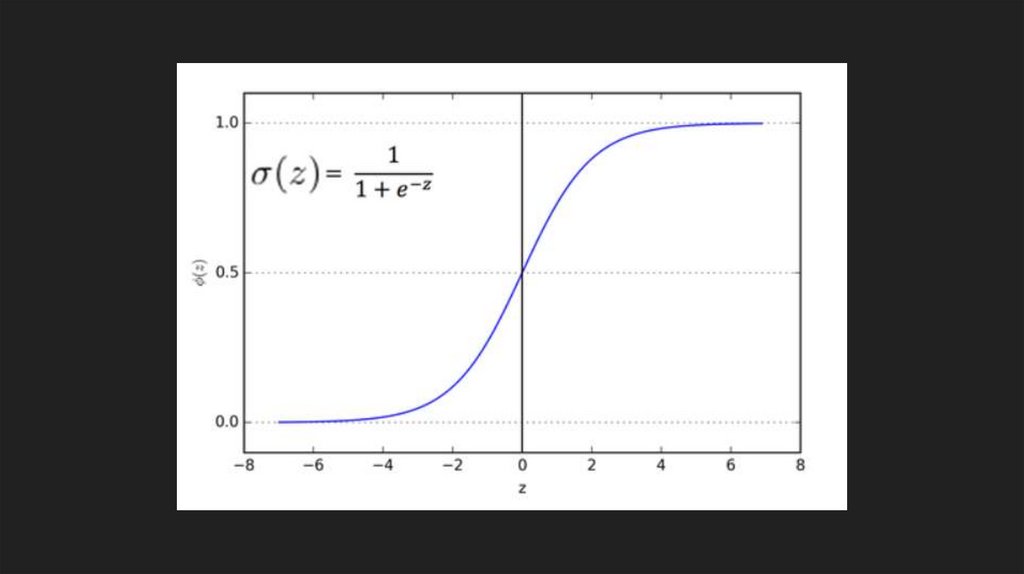
Логистическая регрессия-
Мы хотим предсказывать вероятность принадлежать классу 1
60.
Логистическая регрессия-
Мы хотим предсказывать вероятность принадлежать классу 1
xTw - лежит в R
61.
Логистическая регрессия-
Мы хотим предсказывать вероятность принадлежать классу 1
xTw - лежит в R
62.
63.
Логистическая регрессия(метод максимальногоправдоподобия)
64.
Логистическая регрессия(метод максимальногоправдоподобия)
65.
Многоклассовая классификация-
One vs Rest (для каждого класса тренируем свой классификатор)
66.
Многоклассовая классификация67.
Многоклассовая классификация-
One vs Rest (для каждого класса тренируем свой классификатор)
One vs One (тренируем для каждой пары свой классификатор)
68.
Многоклассовая классификация-
One vs Rest (для каждого класса тренируем свой классификатор)
One vs One (тренируем для каждой пары свой классификатор)
One vs One - дает k(k-1) / 2 - классификатор
69.
Метрики-
Точность
Если большой дисбаланс - точность не работает
70.
Метрики-
Точность
Если большой дисбаланс - точность не работает
Precision - какое кол-во релевантных объектов мы выбрали
71.
Метрики-
Точность
Если большой дисбаланс - точность не работает
Precision - какое кол-во релевантных объектов мы выбрали
Recall - какое кол-во из выбранных нами объектов - релевантно
72.
Метрики73.
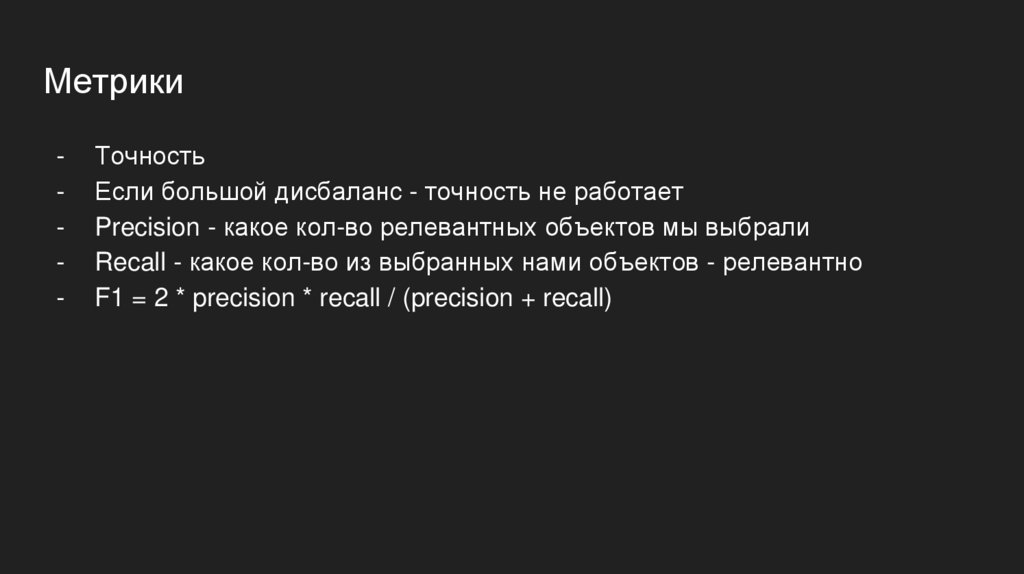
Метрики-
Точность
Если большой дисбаланс - точность не работает
Precision - какое кол-во релевантных объектов мы выбрали
Recall - какое кол-во из выбранных нами объектов - релевантно
F1 = 2 * precision * recall / (precision + recall)
































































 Математика
Математика








