Похожие презентации:
Нелинейная регрессия
1. Нелинейная регрессия
Cтат. методы впсихологии
(Радчикова Н.П.)
Trisha Klass Illinois State University
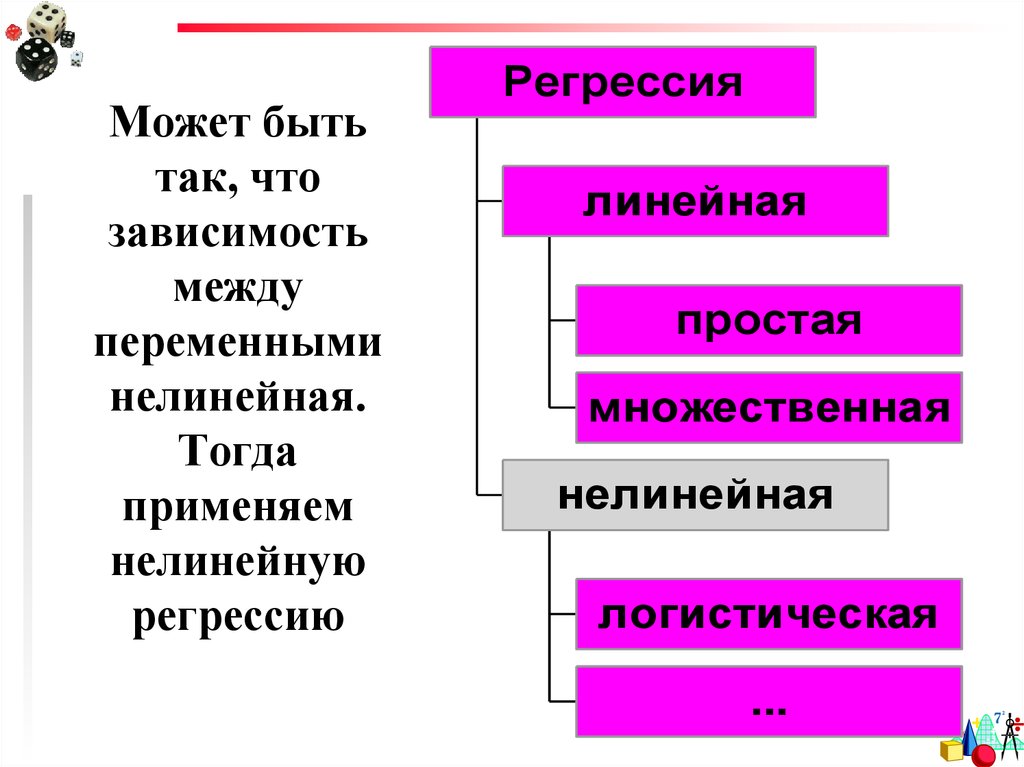
2. Может быть так, что зависимость между переменными нелинейная. Тогда применяем нелинейную регрессию
Регрессиялинейная
простая
множественная
нелинейная
логистическая
...
3.
Бинарная логистическая регрессияпозволяет исследовать зависимость
дихотомических зависимых
переменных от независимых
переменных, имеющих любой вид
шкалы
4.
Бинарная логистическая регрессия отдискриминантного анализа отличается
тем, что связь между зависимой и
независимыми переменными
нелинейная
5. Логистическая регрессия
Мы говорим о некотором событии,которое может произойти или не
произойти. В этом случае вероятность
наступления события рассматривается в
зависимости от значений независимых
переменных.
6. Математическая модель
pгде
1
1 e
z
z=b1x1+b2x2+ …+bnxn+ b0
p – вероятность наступления события, x –
независимые переменные
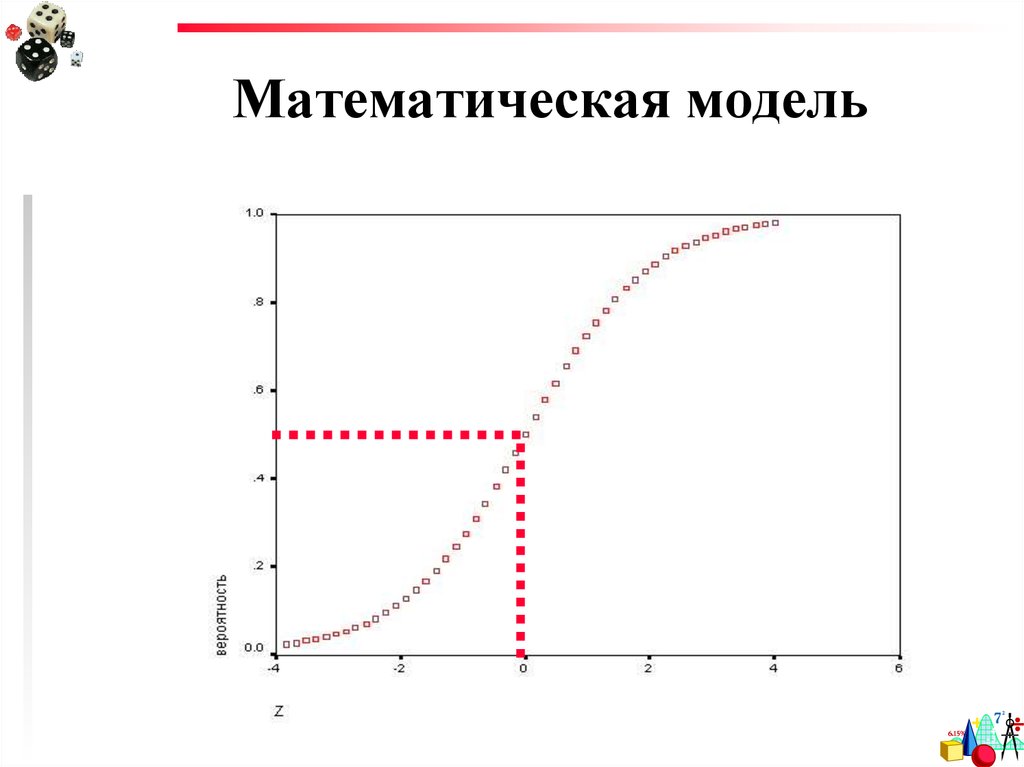
Если р больше 0.5, то можно
предположить, что событие произойдет.
7. Математическая модель
pгде
1
1 e
z
z=b1x1+b2x2+ …+bnxn+b0
Наша задача, как всегда, - оценить
коэффициенты bi
8. Математическая модель
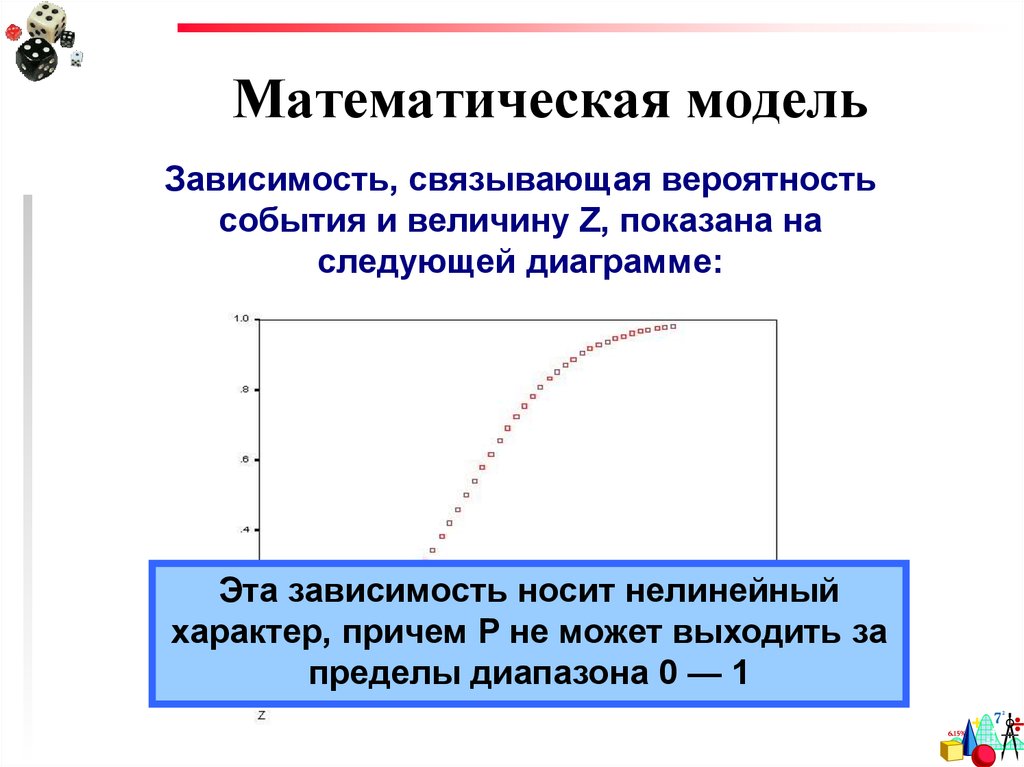
Зависимость, связывающая вероятностьсобытия и величину Z, показана на
следующей диаграмме:
Эта зависимость носит нелинейный
характер, причем P не может выходить за
пределы диапазона 0 — 1
9. Математическая модель
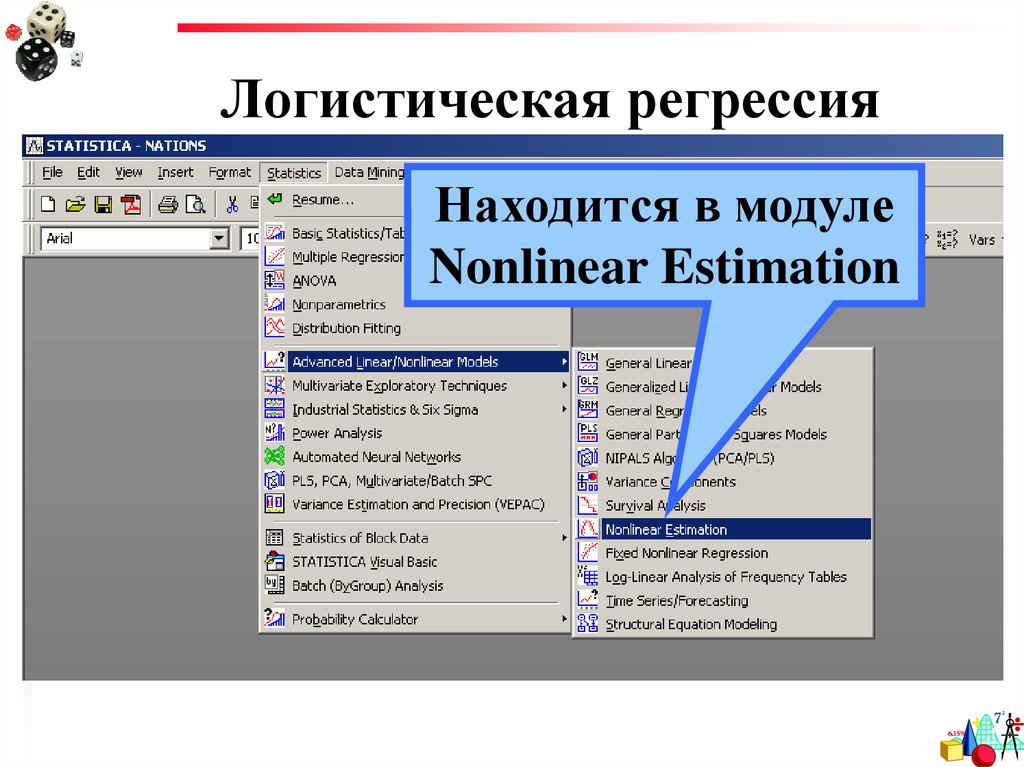
10. Логистическая регрессия
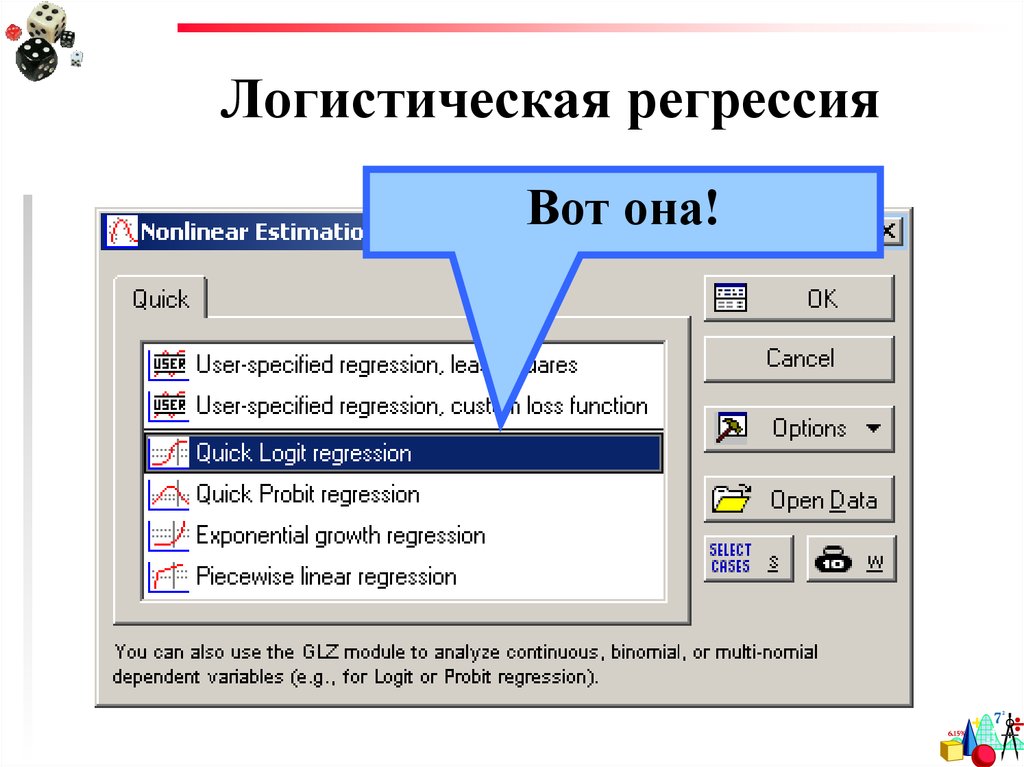
Находится в модулеNonlinear Estimation
11. Логистическая регрессия
Вот она!12. Логистическая регрессия
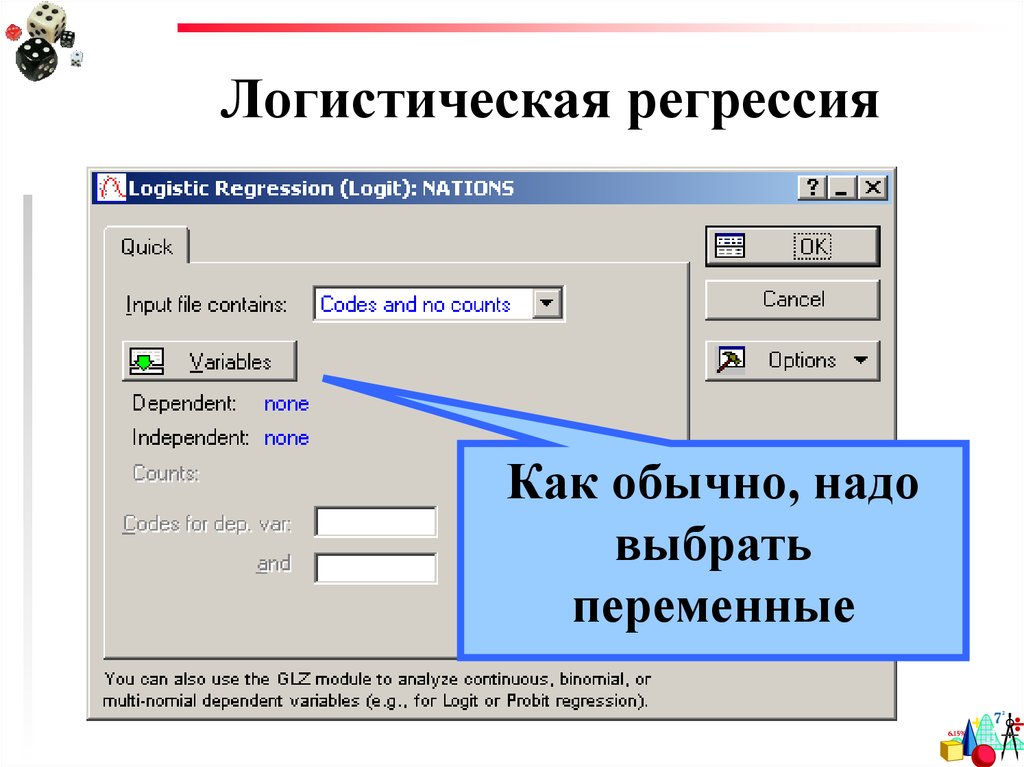
Как обычно, надовыбрать
переменные
13. Пример
Рассмотрим пример из медицины (Breastcancer survival.sta)
Оценим шанс на выживание пациентов
разного возраста с опухолью различных
размеров (две независимые переменные)
14. Пример
Age –Age (years)
Pathsize - Pathologic Tumor Size (cm)
Lnpos -
Positive Axillary Lymph Nodes
…
Status – Censored/Died
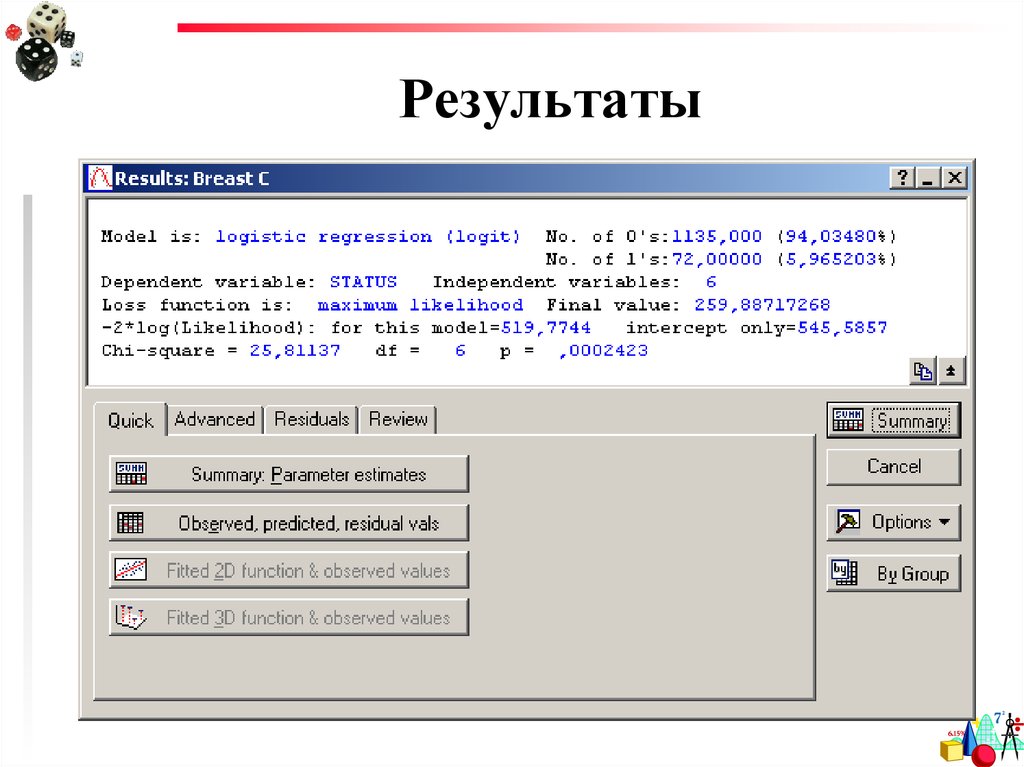
15. Результаты
16. Результаты
Оценка качествамодели
17. Качество модели
Качество приближения регрессионноймодели оценивается при помощи функции
подобия. Мерой правдоподобия служит
отрицательное удвоение значения
логарифма этой функции - -2LL.
В качестве начального значения для -2LL
принимается значение, которое получается
для регрессионной модели, содержащей
только константу.
18. Качество модели
Затем в модель добавляют переменныесогласно выбранному методу и
вычисляют разность (улучшение
качества модели). Разность
обозначают как хи-квадрат и
вычисляют ее значимость.
19. Качество модели
Хи-квадрат20. Результаты
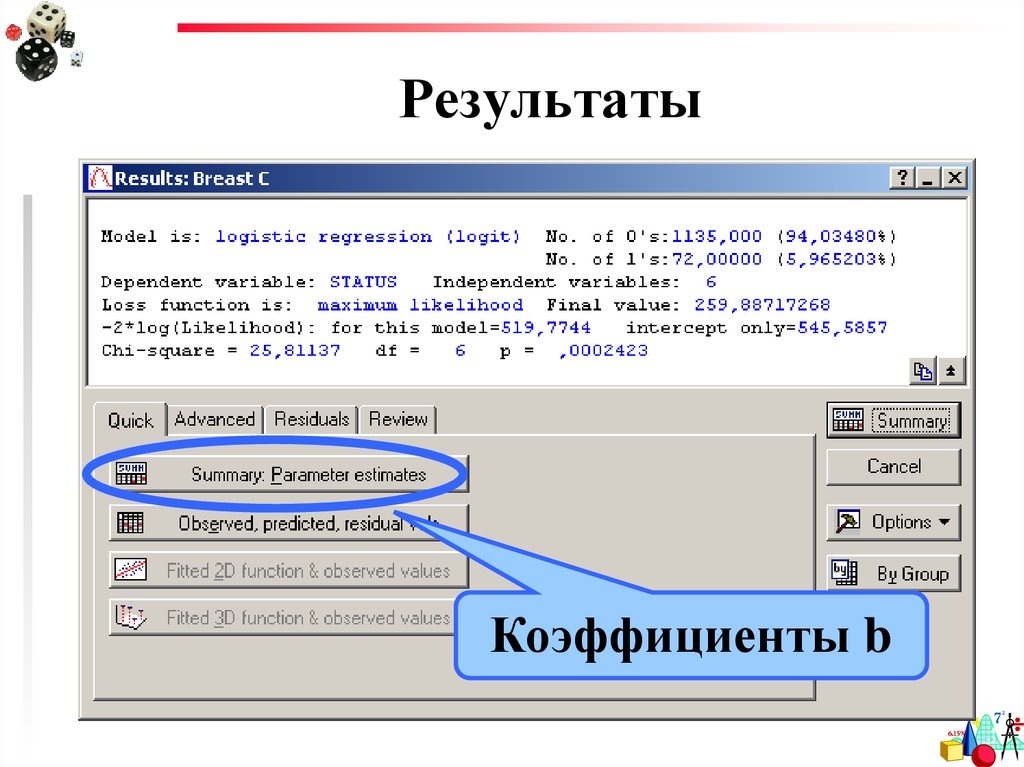
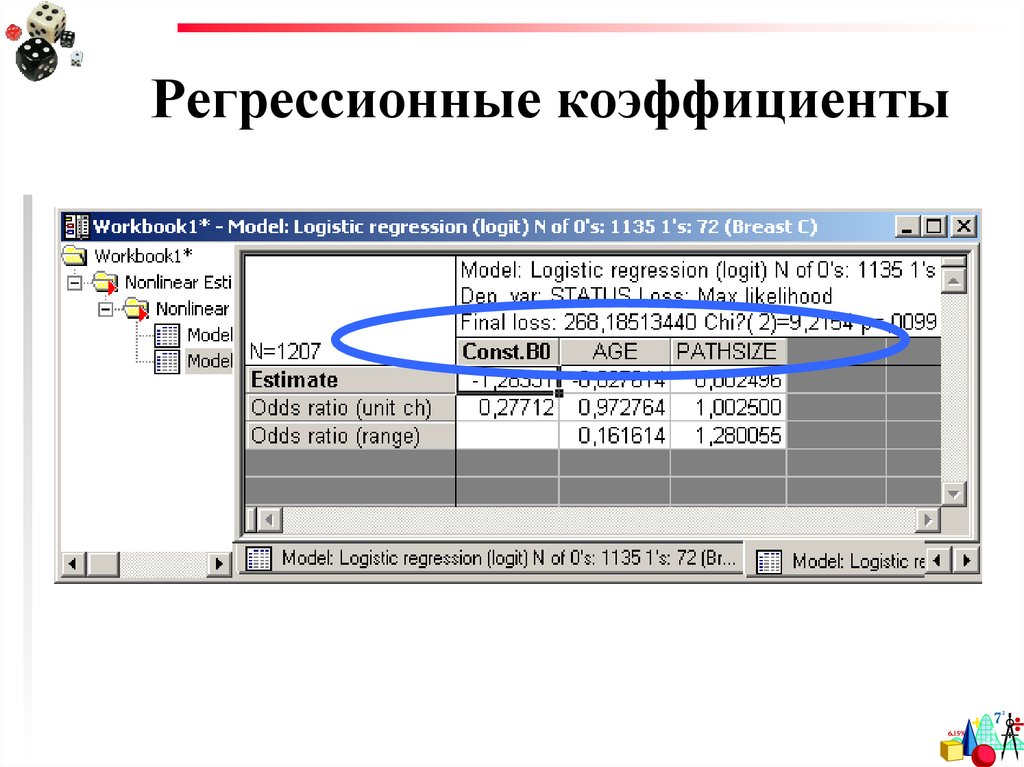
Коэффициенты b21. Регрессионные коэффициенты
22. Результаты
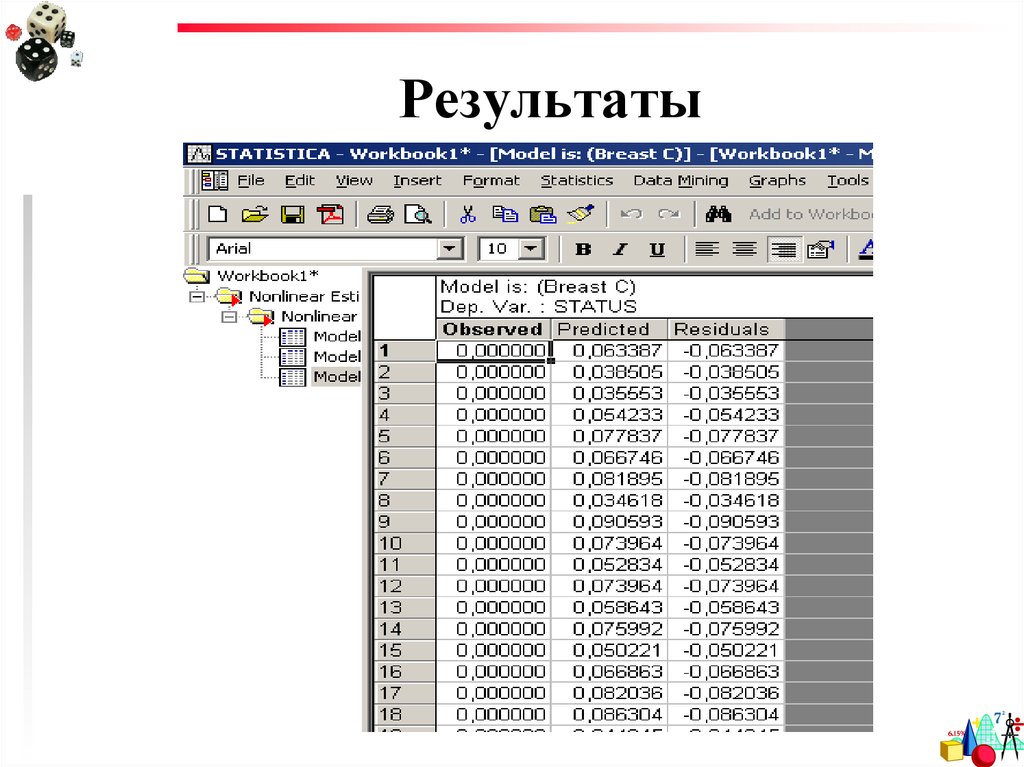
Эмпирические,предсказанные
значения и остатки
23. Результаты
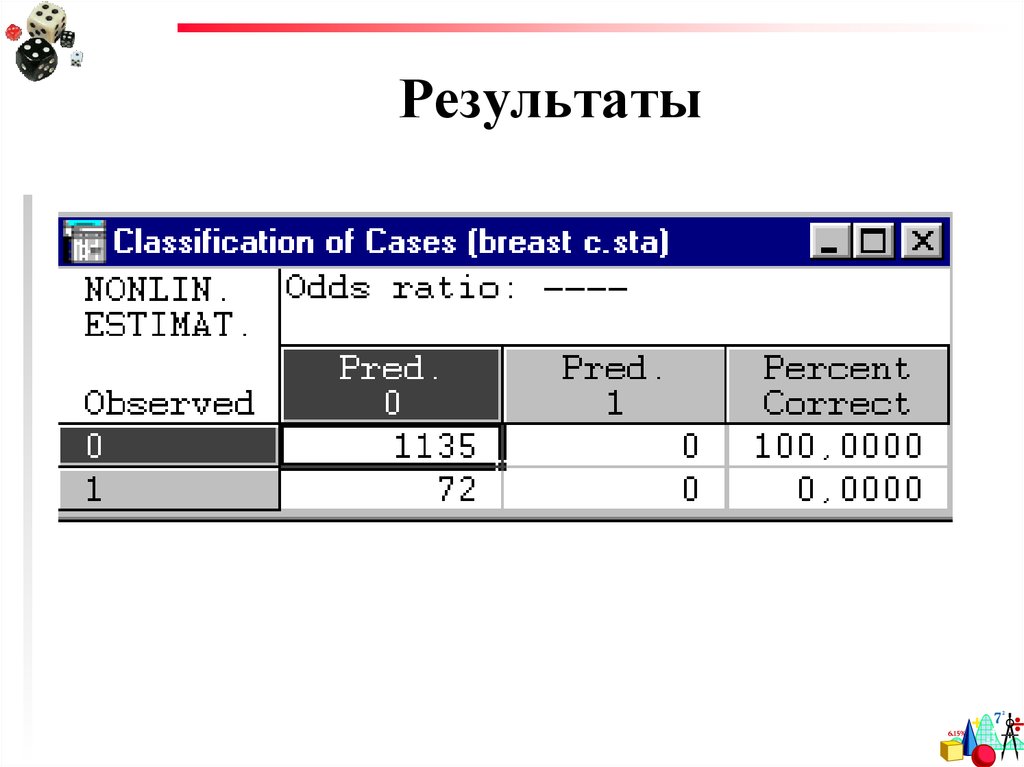
24. Результаты
Матрицаклассификации
25. Результаты
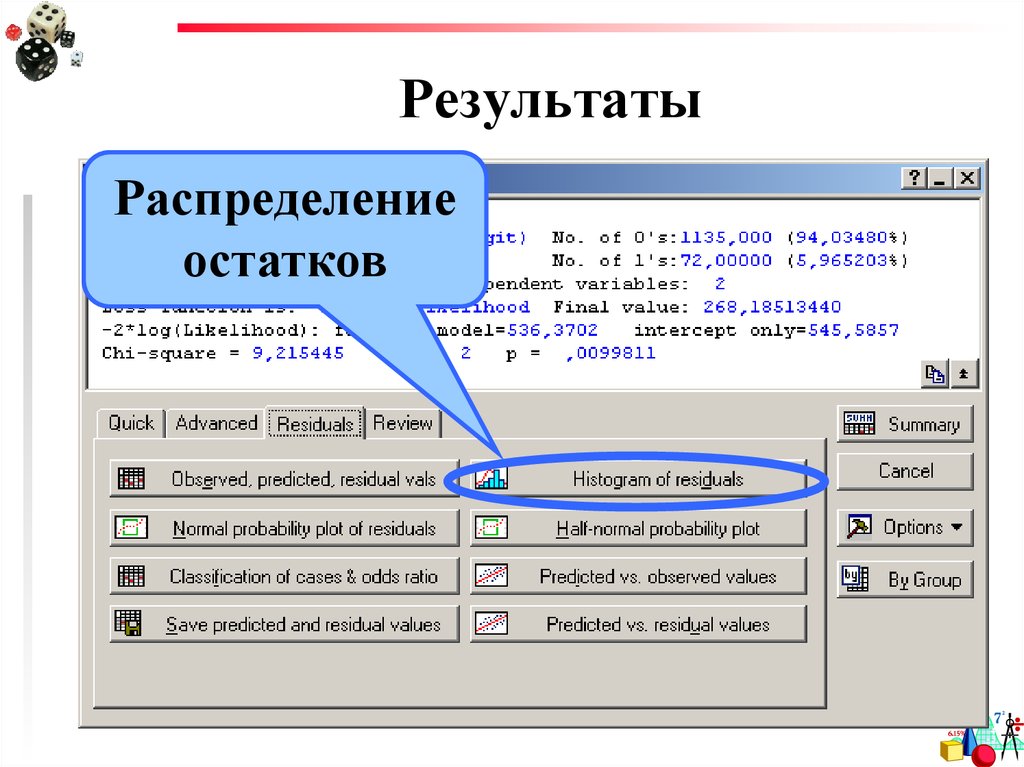
26. Результаты
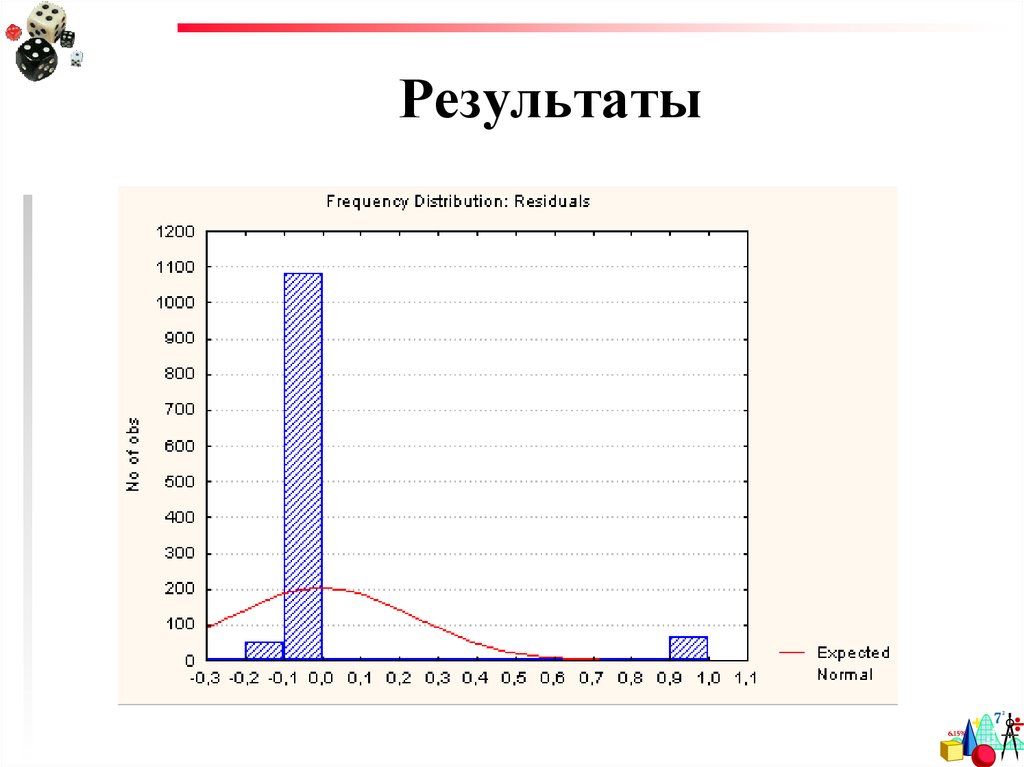
Распределениеостатков
27. Результаты
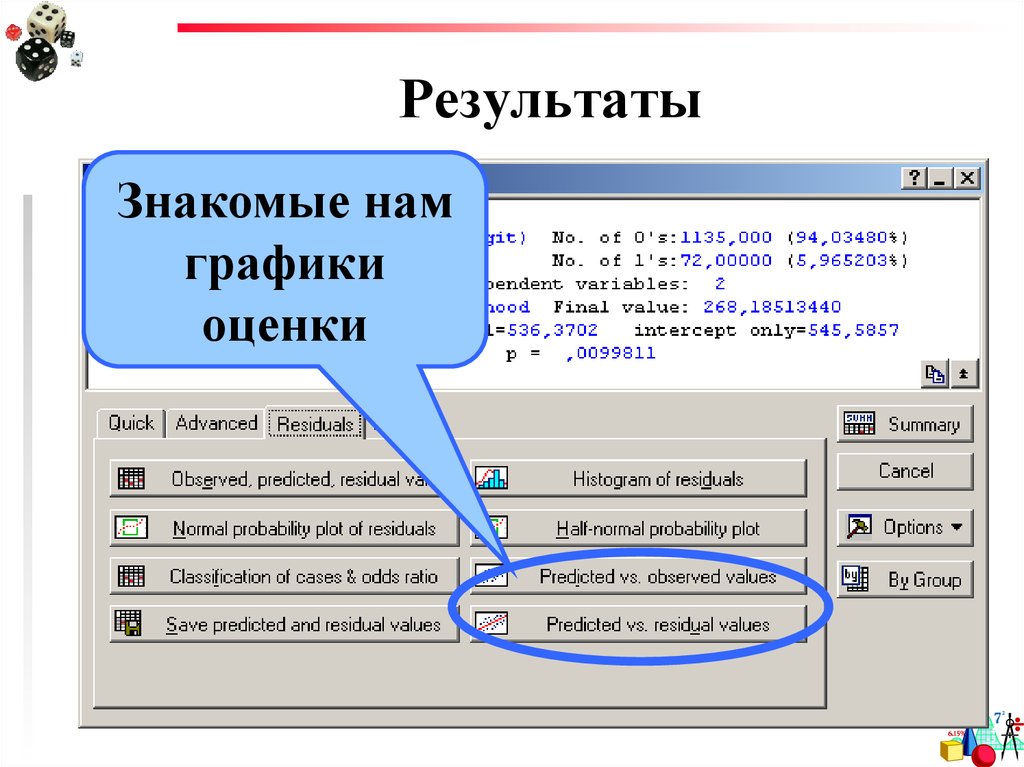
28. Результаты
Знакомые намграфики
оценки
29.
А если уменя такая
зависимость,
какую я сам
придумал ?!
30.
ph(t)h'
c
1 e ia bt
log cov(h(t)g(
c
t)n 1 e
Оценка на экзамене и
мотивация так прямо не
связаны …
a bt
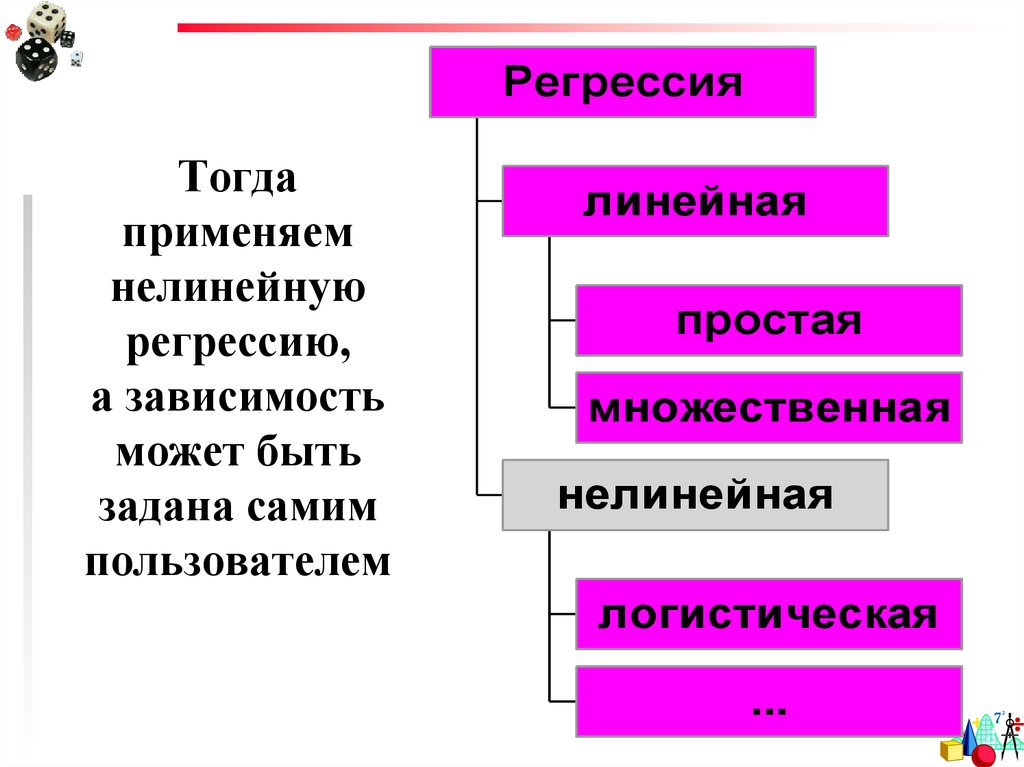
31. Тогда применяем нелинейную регрессию, а зависимость может быть задана самим пользователем
РегрессияТогда
применяем
нелинейную
регрессию,
а зависимость
может быть
задана самим
пользователем
линейная
простая
множественная
нелинейная
логистическая
...
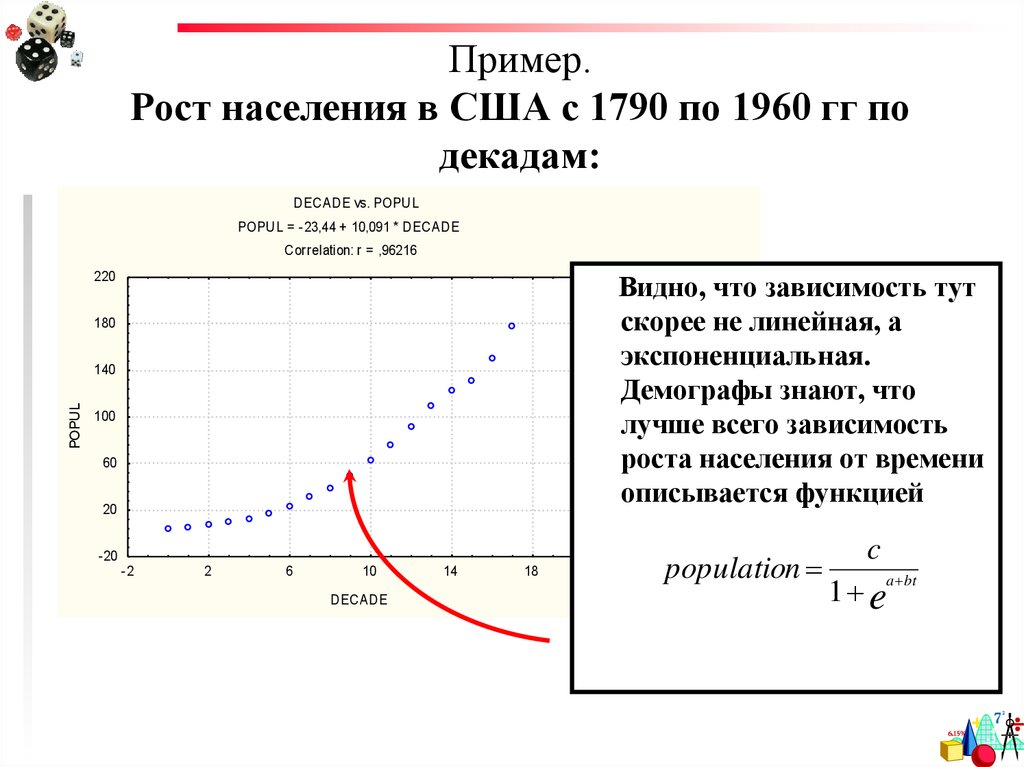
32. Пример. Рост населения в США с 1790 по 1960 гг по декадам:
D EC AD E vs. POPU LPOPU L = -23,44 + 10,091 * D EC AD E
C orrelation: r = ,96216
220
Видно, что зависимость тут
скорее не линейная, а
экспоненциальная.
Демографы знают, что
лучше всего зависимость
роста населения от времени
описывается функцией
180
POPUL
140
100
60
20
-20
-2
2
6
10
D EC AD E
14
18
22
R eg ression
95% confid.
population
c
a bt
1 e
33.
Очевидно, что нашей задачейявляется определение трех
коэффициентов - a, b и c.
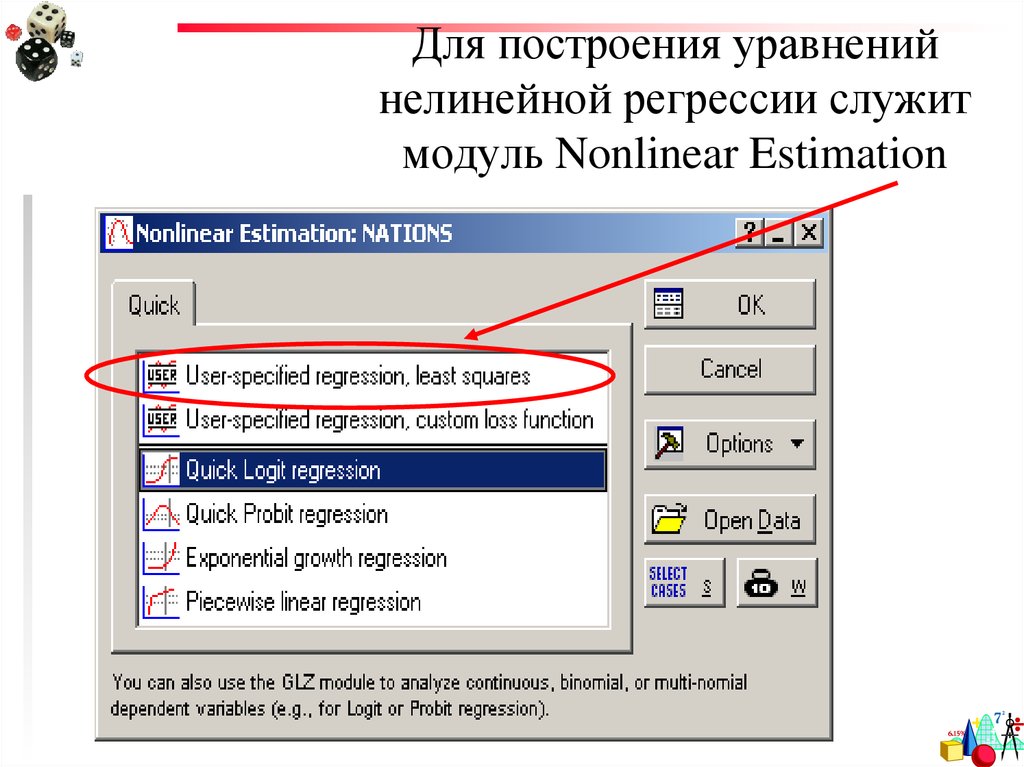
34. Для построения уравнений нелинейной регрессии служит модуль Nonlinear Estimation
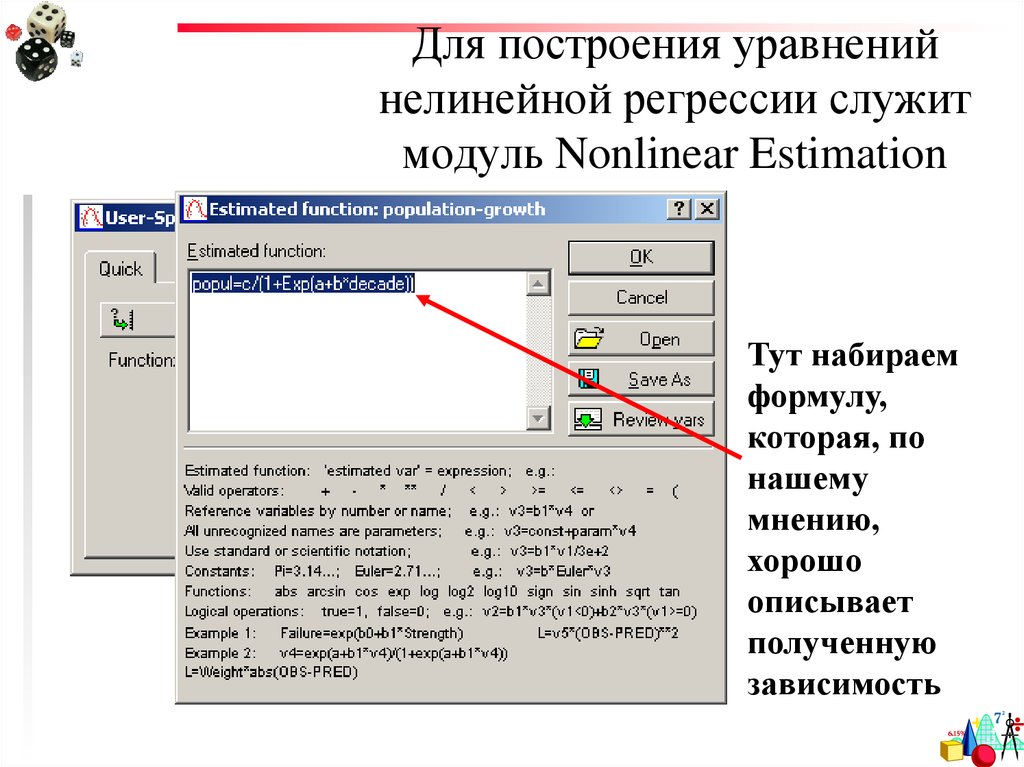
35. Для построения уравнений нелинейной регрессии служит модуль Nonlinear Estimation
Тут набираемформулу,
которая, по
нашему
мнению,
хорошо
описывает
полученную
зависимость
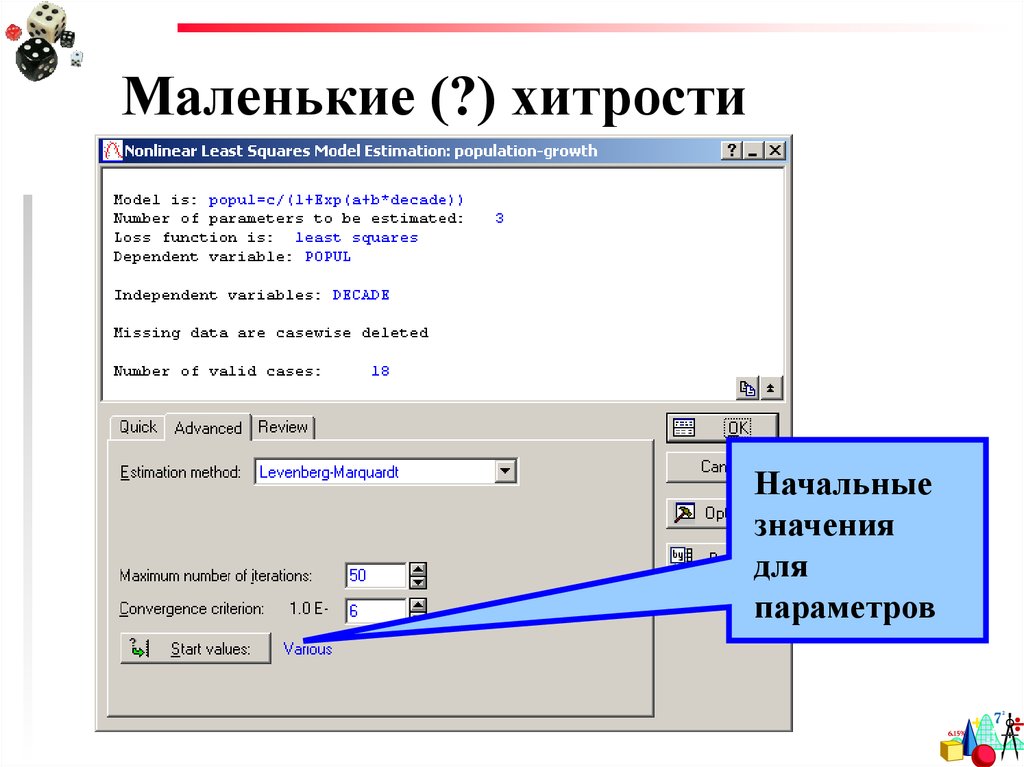
36.
Маленькие (?) хитростиНачальные
значения
для
параметров
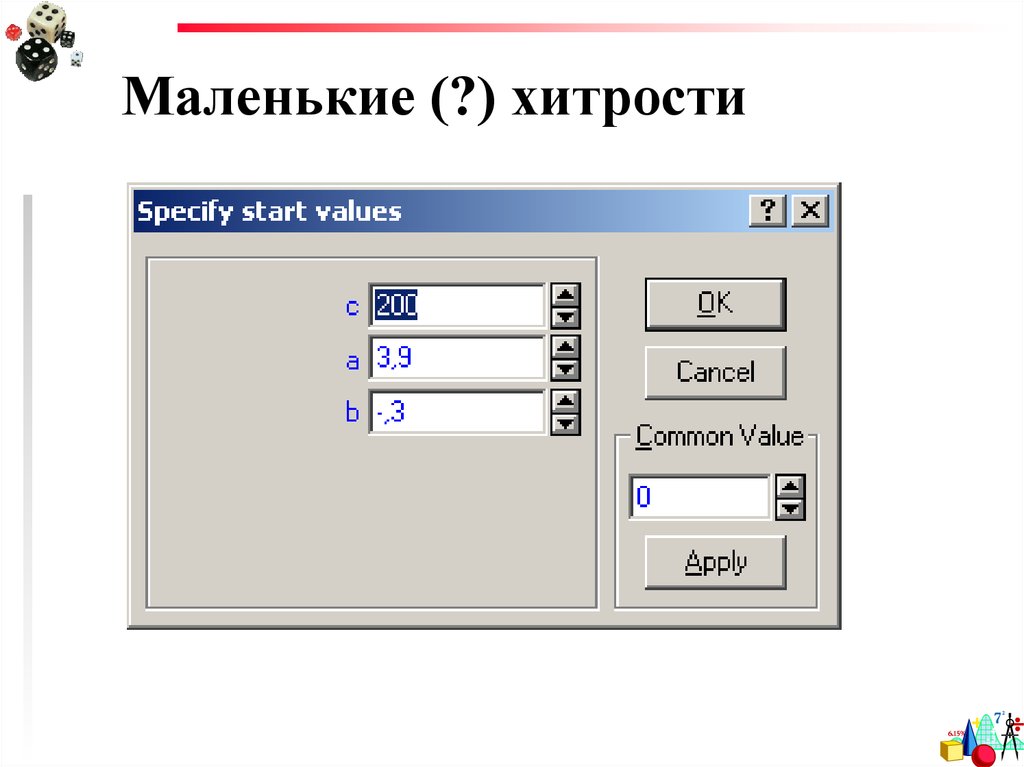
37.
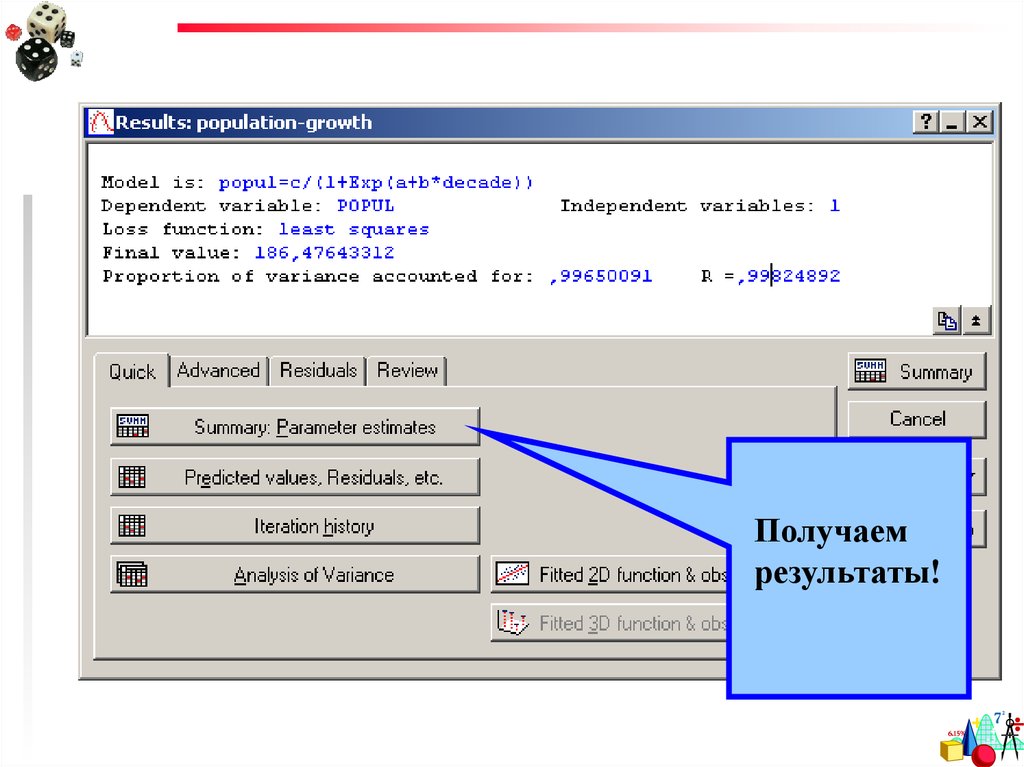
Маленькие (?) хитрости38.
Получаемрезультаты!
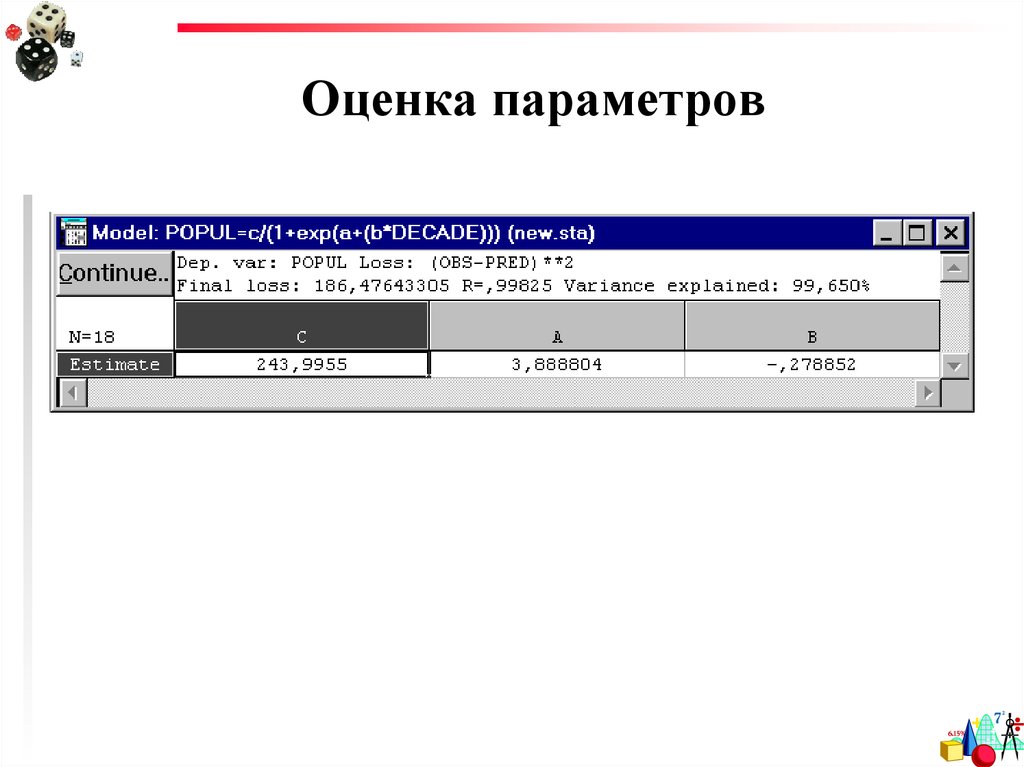
39. Оценка параметров
40.
Теперь,подставив коэффициенты
в исходную формулу
population
244
3, 89 0 , 28t
1 e
,
мы можем оценить население
США в будущем - через 19, 20,
1000 лет…
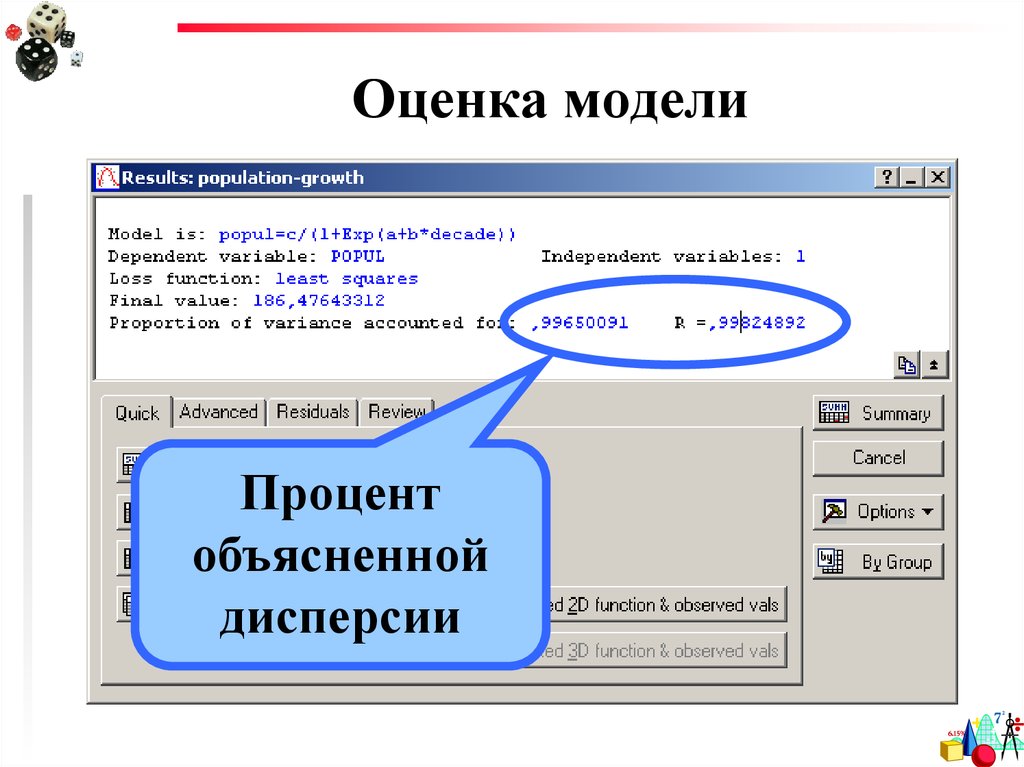
41. Оценка модели
Процентобъясненной
дисперсии
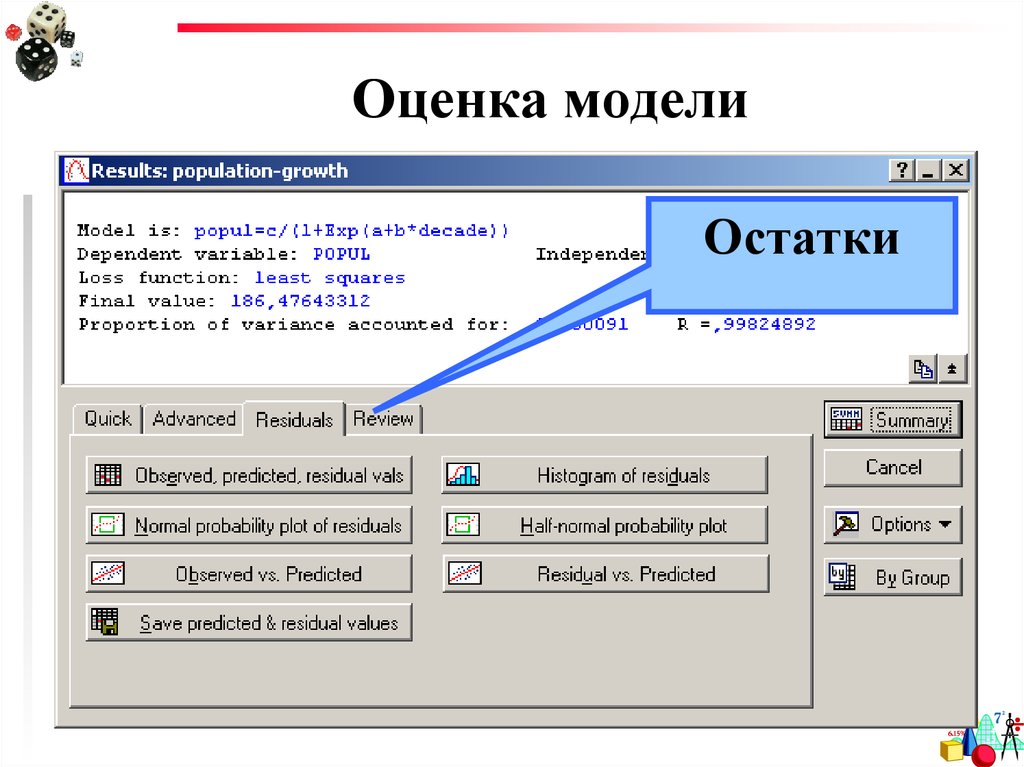
42. Оценка модели
Остатки43. Оценка модели
Эмпирические,предсказанные
значения и
остатки
44. Оценка модели
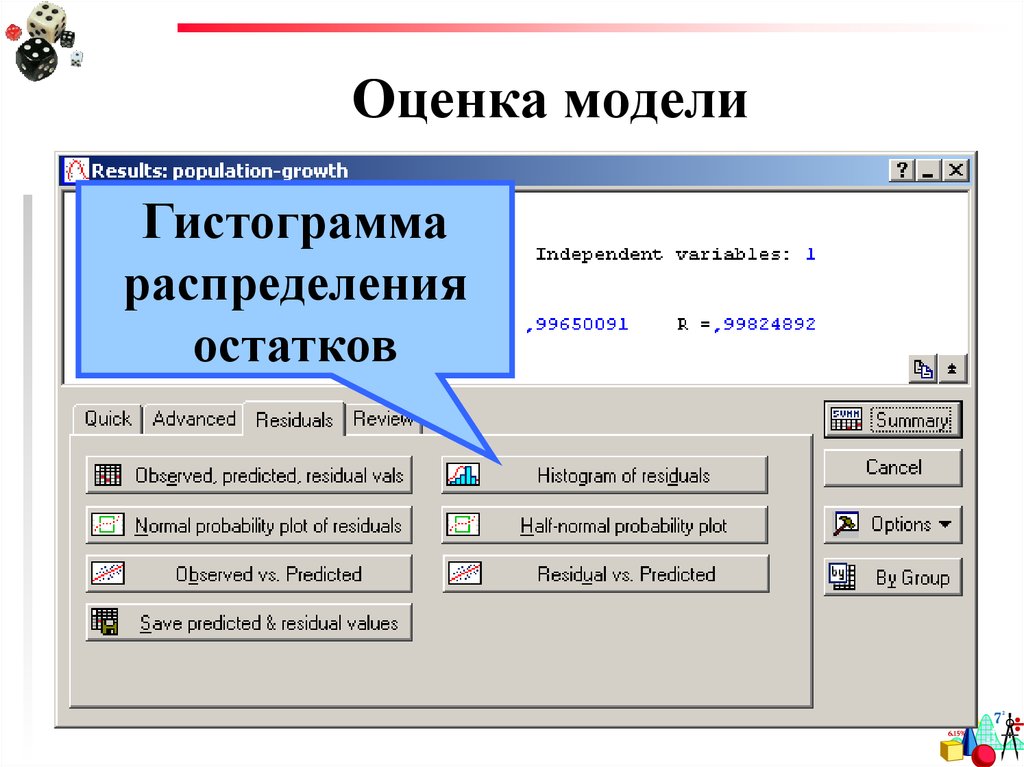
Гистограммараспределения
остатков
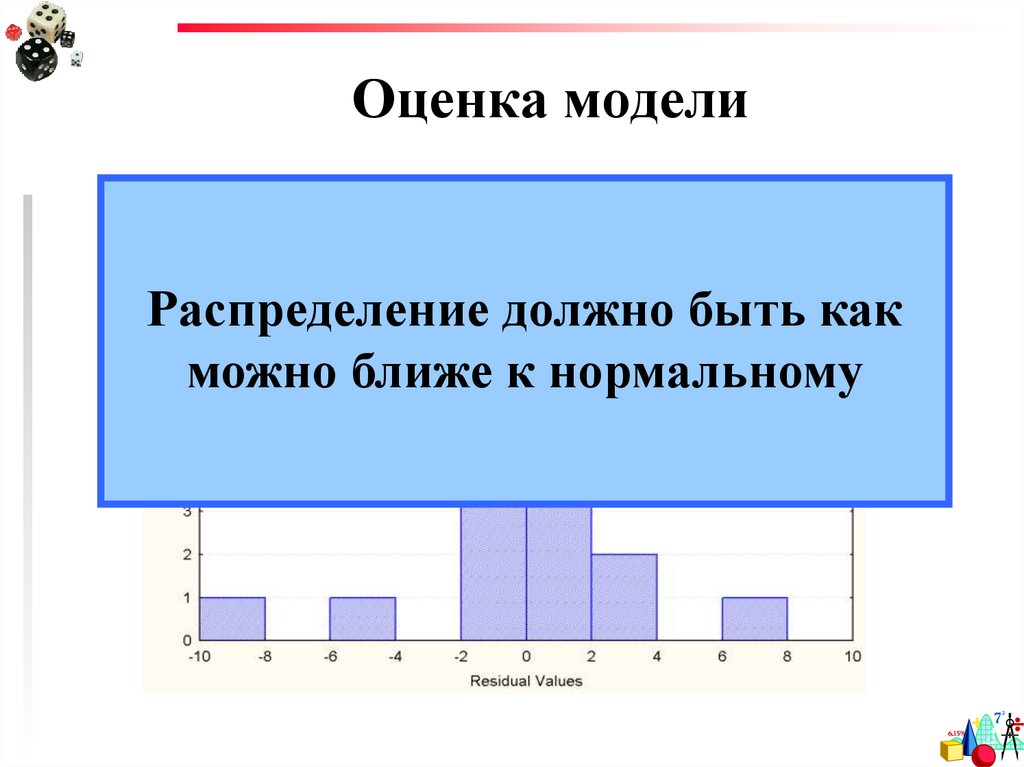
45. Оценка модели
Распределение должно быть какможно ближе к нормальному
46. Оценка модели
ТожеГистограмма
знакомые
распределения
нам графики
остатков
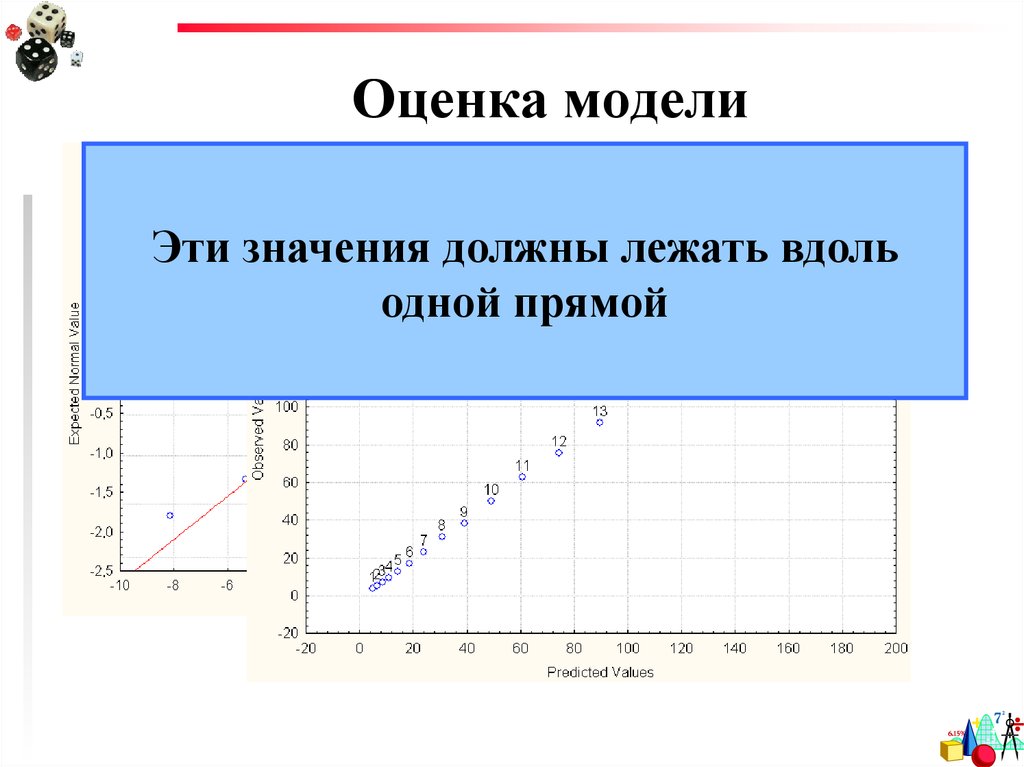
47. Оценка модели
Эти значения должны лежать вдольодной прямой
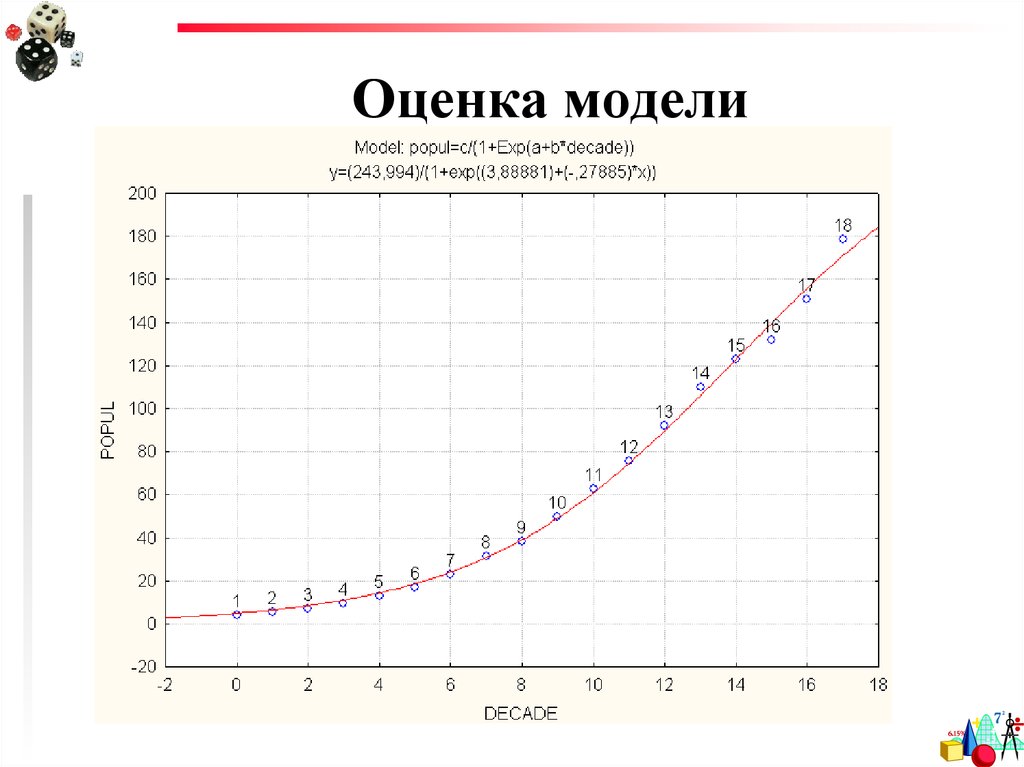
48. Оценка модели
График эмпирическихзначений и функции,
описывающей модель
49. Оценка модели
50.
Вот и все!Задавайте любые зависимости
и проверяйте любые модели!






















 Математика
Математика








