Паралельне перенесення

1. Паралельне перенесення

2.

Паралельним перенесенням називають
таке перетворення фігури, при якому всі її
точки зміщуються в одному й тому самому
напрямі на одну й ту саму відстань.
р

3.

Паралельним перенесенням називають таке
перетворення фігури, при якому її довільна точка
М(х; у) переходить у точку М'(х + а; у + b), де а і b одні й ті самі для всіх точок фігури.
Якщо точка Мʹ має координати (хʹ; уʹ), то отримаємо формули
паралельного перенесення
хʹ = х + а
уʹ = у + b

4.

Розв'язання: 1)Якщо точка А переходить в точку Аʹ, то точка Аʹ матиме
координати хʹ = х + 2; уʹ = у – 3, отже Аʹ(5 + 2; 4 – 3) = Аʹ(7; 1).
2) Якщо точка В переходить в точку Вʹ, і точка Вʹ має координати хʹ = х + 2;
уʹ = у – 3, то точка В(х; у) матиме координати х = хʹ – 2; у = уʹ + 3.
Отже, В(– 7 – 2; –3 +3) = В(– 9; 0).
Розв'язання: Вектор паралельного перенесення можна визначити за формулами
хʹ = х + а; уʹ = у + b, де а = 4 – 2 = 2, b = 9 – (– 5) =14. Отже, шукані формули
матимуть вигляд: хʹ = х + 2; уʹ = у + 14

5.

ВЛАСТИВОСТІ ПАРАЛЕЛЬНОГО
ПЕРЕНЕСЕННЯ
1. Паралельне перенесення є переміщенням
2. Паралельне перенесення є рухом.
3. При паралельному перенесенні точки переміщуються
вздовж паралельних прямих (або однієї прямої) на ту
саму відстань.
4. Пряма переходить у паралельну пряму (або в себе);
промінь переходить у співнапрямлений промінь.

6.

тканини
шпалери
рушники

7.

8.

9.

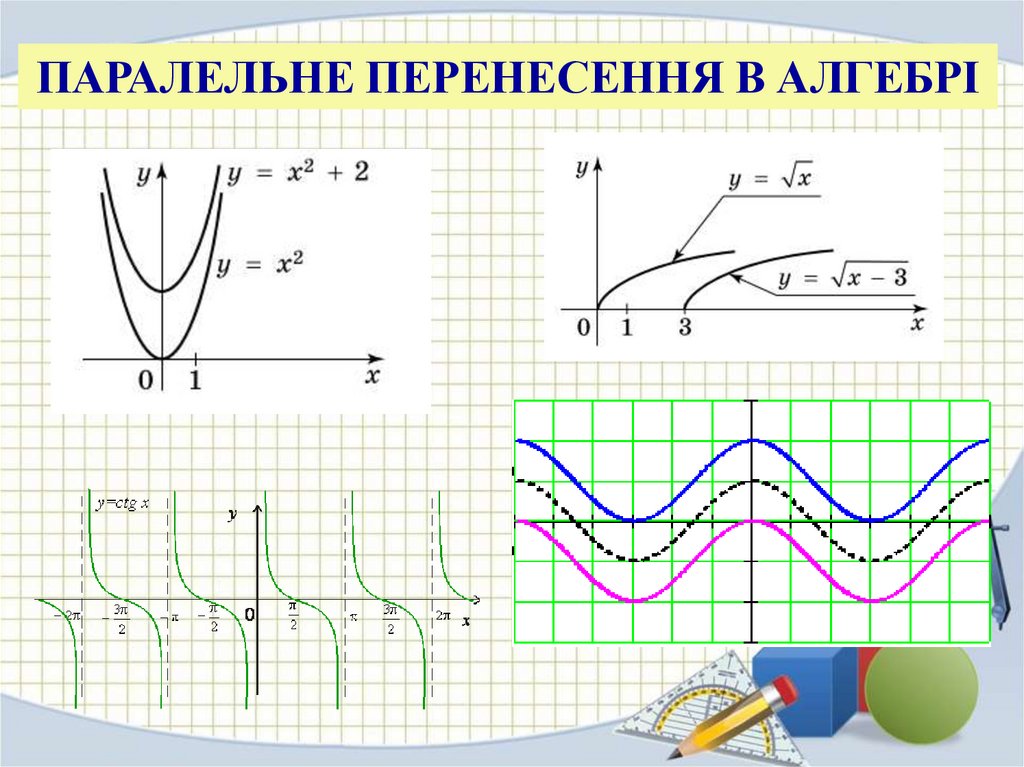
ПАРАЛЕЛЬНЕ ПЕРЕНЕСЕННЯ В АЛГЕБРІ

10.

НІ
ТАК
НІ
ТАК
Оʹ(-2; 5)
Аʹ(1; 4)
Вʹ(0; 0)
Сʹ(8; 6)

11.

Розв'язання: 1) Якщо точка А переходить в точку Аʹ, то вектор
переносу ААʹ буде мати координати ААʹ: а = –4 – 2 = –6, b = 5 – 7 = – 2,
отже формули паралельного перенесення можна записати у вигляді
хʹ = х – 6; уʹ = у – 2.
2) Якщо точка А переходить в точку Аʹ, то вектор переносу ААʹ буде
мати координати ААʹ: а = 2 + 1 = 3, b = –5 –3 = –8, отже формули
паралельного перенесення можна записати у вигляді хʹ = х + 3;
уʹ = у – 8.
Відповідь: 1) хʹ = х – 6; уʹ = у – 2;
2) хʹ = х + 3; уʹ = у – 8.

12.

Розв'язання: 1)Якщо точка А переходить в точку В, то її вектор переносу буде
АВ( 4 – 2; – 7 –(– 1)) = АВ(2; – 6). Якщо точка С переходить в точку D, то її
вектор переносу буде СD( 2–0; – 3 – 2) = СD(2; – 5). Вектори АВ і СD не рівні,
отже, такого паралельного перенесення не існує.
2)Якщо точка М переходить в точку N, то її вектор переносу буде MN(0 – 4; –
3+2) = MN(– 4; – 1). Якщо точка К переходить в точку L, то її вектор переносу
буде КL(– 1 – 3; – 1 – 0) = КL(– 4; –1). Вектори MN і КL рівні, отже, таке
паралельне перенесення існує.
Відповідь: 1) не існує; 2) існує

13.

Домашнє завдання
Опрацювати § 11.
Виконати №360-365 - графічні вправи,
№371 - розв'язати.