Основные уравнения электростатики в вакууме или математическое описание электростатического поля. Лекция 2

1.

Лекция № 2
ОСНОВНЫЕ УРАВНЕНИЯ
ЭЛЕКТРОСТАТИКИ В ВАКУУМЕ
ИЛИ МАТЕМАТИЧЕСКОЕ
ОПИСАНИЕ
ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ
58
1

2.

ВОПРОСЫ
6. Поток вектора напряжённости
электрического поля. Теорема
Остроградского-Гаусса.
7. Циркуляция вектора Е.
Теорема Стокса.
8. Проводники в электрическом поле.
Явление электростатической
индукции.
58
2

3.

6. Поток вектора напряжённости
электрического поля.
Теорема Остроградского-Гаусса и её
применение для расчёта полей
заряженных плоскости, цилиндра и
сферы.
58
3

4.

Градиент – вектор, направленный в
сторону наибольшего возрастания
потенциала поля
gradφ φ E
58
4

5.

Напряжённость вектора Е
направлена в сторону убывания
потенциала φ.
Оператор «набла» или Гамильтона
(гамильтониан)
i
j k
x
y
z
58
5

6.

Эквипотенциальные поверхности –
поверхности равного потенциала или
поверхности где потенциал имеет
одно и тоже значение (φ = const).
58
6

7.

Из выражения
gradφ E
следует, что в электростатическом
поле линии напряжённости
пересекают эквипотенциальные
поверхности под прямым углом.
58
7

8.

Поток вектора напряжённости
электрического поля называют
интеграл по поверхности от
скалярного произведения векторов
Е и dSn.
Ф E dS n EdS cos α En dS
E
S
S
S
58
8

9.

α – угол между векторами Е и n.
58
9

10.

Теорема Остроградского-Гаусса
(Гаусса) в интегральной форме:
Поток вектора Е сквозь
произвольную замкнутую
поверхность, охватывающую заряд,
пропорционален алгебраической
сумме зарядов:
1
Q
Ф E dS n qi
E
ε0
ε 0 i 1
S
N
58
10

11.

Введём понятия плотности заряда:
объёмной ρ, поверхностной σ,
линейной λ (или τ).
1
ρ q
V
1
σ q
S
1
λ q
L
где V – объём пространства,
S – площадь поверхности,
L – длина линии.
58
11

12.

Если полный поток вектора
напряжённости ФЕ поделить на
объём V, который стремится к нулю,
то получим плотность зарядов
делённую на постоянную ε0.
Полученное выражение называться
теоремой Гаусса в
дифференциальной форме или
дивергенцией вектора Е.
58
12

13.

1
ρ
divE lim E dSn
V 0 V
ε0
S
58
13

14.

Дивергенция – это плотность
источников поля.
С точки зрения математики имеем
оператор – сумма частных
производных по трём направлениям
(оператор набла, но в отличии от
градиента, действие совершаем над
вектором и получаем скаляр)
Ex E y Ez
ρ
E
divE
x
y
z
ε0
58
14

15.

Применение теоремы Гаусса
58
15

16.

Электрическое поле равномерно
заряженной бесконечной плоскости.
Дана бесконечная плоскость,
равномерно заряженная с
поверхностной плотностью заряда
σ = q/S.
58
16

17.

Из свойств симметрии следует, что
вектор напряжённости
электрического поля, созданного
этой плоскостью, всюду
перпендикулярен ей и имеет
постоянное значение E = const.
58
17

18.

Исходя из этого, выберем замкнутую
поверхность, например
цилиндрическую, и располагаем её
так, что вектор Е перпендикулярен
плоскости оснований и параллелен
боковой поверхности.
58
18

19.

58
19

20.

Таким образом, поток вектора Е
через боковую поверхность равен
нулю.
Полный поток вектора Е,
пронизывающий цилиндрическую
поверхность
ФЕ = 2ЕS + 0 = 2ЕS.
58
20

21.

Согласно теореме Гаусса
1 N
Ф E dSn qi
Е S
ε 0 i 1
где
n
q qi σS
i 1
σS
σ
следовательно 2 ES
, E
2ε 0
ε0
58
21

22.

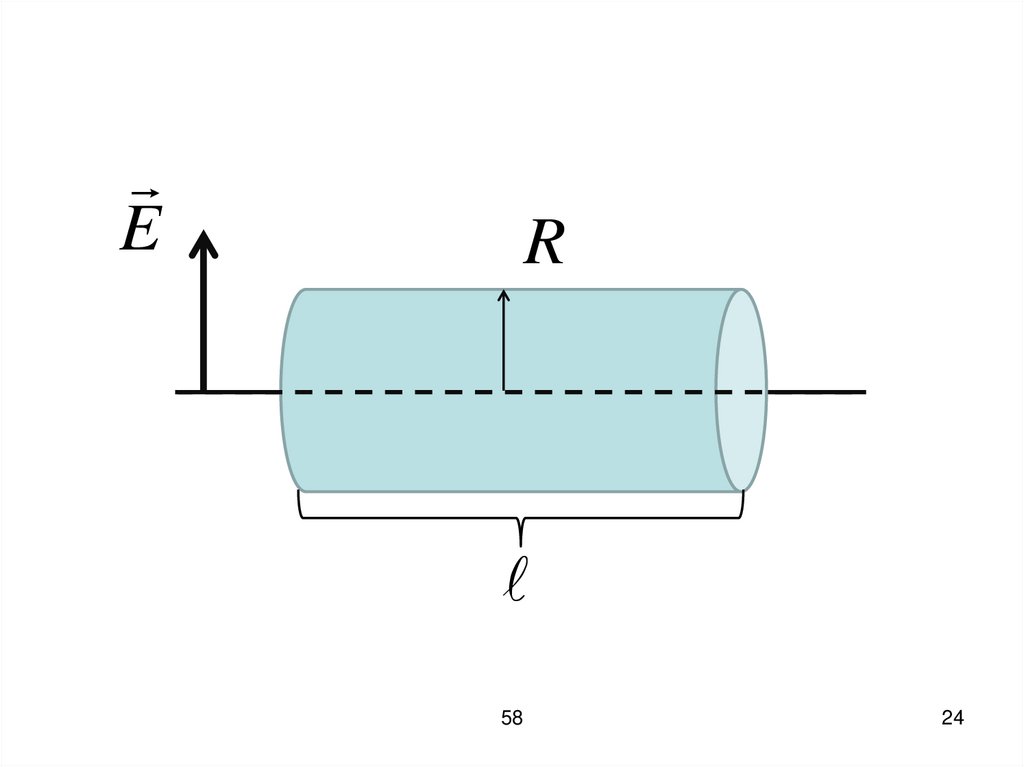
Электрическое поле равномерно
заряженной бесконечной нити.
Дана бесконечная нить с линейной
плотностью заряда
q
λ τ
58
22

23.

Исходя из свойств симметрии
выбираем цилиндрическую
поверхность, ось которой совпадает
с нитью.
В данном случае вектор Е
перпендикулярен боковой
поверхности, параллелен
основанию.
Следовательно, поток вектора Е
через основания будет равен нулю.
58
23

24.

E
R
58
24

25.

Согласно теореме Гаусса
1 N
Ф E dSn ES qi
Е S
ε 0 i 1
n
где q qi τ , S 2πR
i 1
следовательно
E 2πR
τ
E
2πRε 0
τ
ε0
58
25

26.

Поле равномерно заряженной
сферы
Пусть сферическая поверхность
радиуса R заряжена равномерно с
поверхностной плотностью заряда
+ .
Электрическое поле заряженной
сферы центрально-симметричное.
58
26

27.

Силовые линии напряженности
направлены от поверхности на
продолжение радиусов, а модуль
вектора Е должен зависеть только от
расстояния до поверхности сферы.
58
27

28.

В качестве замкнутой поверхности
проще всего использовать
концентрическую сферу радиуса r,
проходящую через ту точку
электрического поля, в которой
требуется определить
напряженность этого поля.
58
28

29.

Рассмотрим три случая:
а) r R.
Внутри сферы зарядов нет.
Все заряды расположены на
внешней поверхности сферы, т. е. в
любой точке внутри сферы Е = 0.
58
29

30.

58
30

31.

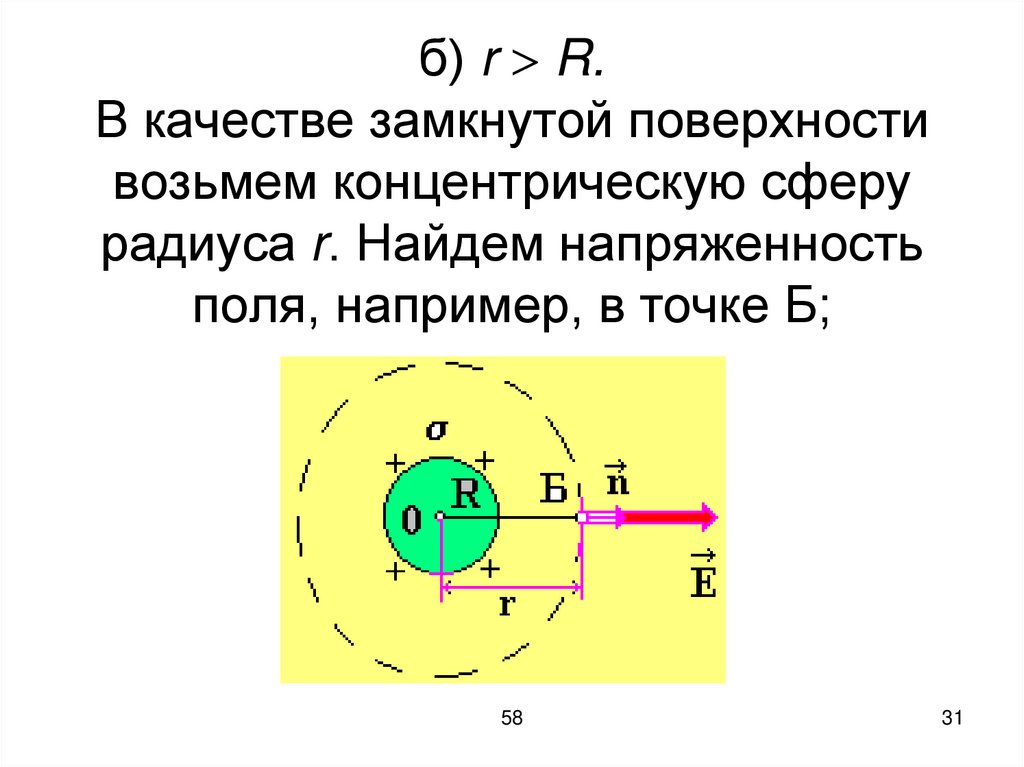
б) r R.
В качестве замкнутой поверхности
возьмем концентрическую сферу
радиуса r. Найдем напряженность
поля, например, в точке Б;
58
31

32.

Поток вектора Е, т. е. ФЕ = Е·Sr
(Е = Еn, Е n ),
где Sr = 4 r2 площадь сферической
поверхности радиуса r.
Согласно теореме Гаусса поток
вектора Е
1
1 N
Ф E dSn qi σSсферы
E S
ε 0 i 1
ε0
58
32

33.

Таким образом
1
2 1
E 4πr q σ 4πR
ε0
ε0
2
q
σ R
E или E
2
4π ε 0 R
ε0 r
2
где q суммарный заряд.
58
33

34.

График изменения напряженности
электрического поля заряженной
сферической поверхности от
расстояния.
58
34

35.

58
35

36.

Вопрос 7.
Циркуляция вектора Е.
Теорема Стокса.
58
36

37.

Циркуляцией вектора Е по
произвольному замкнутому пути L
называют интеграл
(*)
E d
L
58
37

38.

Домножим интеграл (*) на величину
заряда q, который перемещаем по
пути L:
q
F
d
A
E
d
d
L
L
(**)
L
58
38

39.

Электростатическое поле –
потенциальное поле, а силы
электростатического поля –
консервативные силы.
Следовательно, циркуляция вектора
Е электростатического поля равна
нулю
(интегралы (*), (**) равны нулю):
E d 0.
L
58
39

40.

Интеграл по незамкнутому пути L
также равен нулю, если
перемещение идёт по
эквипотенциальной поверхности или
перпендикулярно вектору Е.
58
40

41.

Ротор – величина, равная
отношению
интеграла
к
площади
S,
охватываемой
E
d
L
контуром L, при S→0:
1
rotE lim
E
d
S 0
SL
58
41

42.

i
rotE E
x
Ex
58
j
y
Ey
k
z
Ez
42

43.

Теорема Стокса
E d rotE dS n
L
S
58
43

44.

58
44

45.

Вопрос 8.
Проводники в электрическом поле.
Явление электростатической
индукции.
Граничные условия.
58
45

46.

Проводники – вещества, заряды
которых способны перемещаться
внутри проводника на
макроскопические расстояния.
58
46

47.

Носители электрического тока в
металлах – квазисвободные
электроны:
в электролитах – положительные и
отрицательные ионы;
в ионизированных газах – ионы и
свободные электроны.
58
47

48.

Рассмотрим однородное
электростатическое поле (Е=const).
58
48

49.

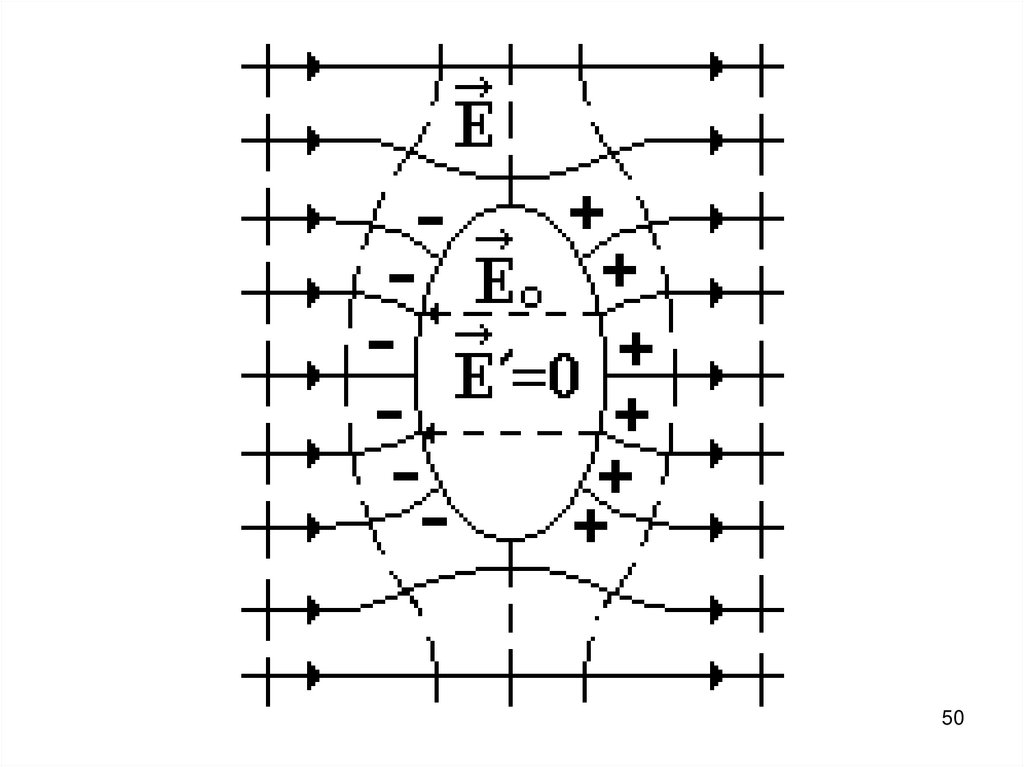
Внесем проводник во внешнее
электрическое поле. Под действием
внешнего электрического поля
электроны будут перемещаться
против поля, создавая избыточный
отрицательный заряд на левой
поверхности проводника. Справа
останется избыточный
положительный заряд.
58
49

50.

58
50

51.

Внутри проводника возникнет
собственное электрическое поле Е0.
Вектор напряженности Е0
собственного электрического поля Е0
противоположно направлен вектору
напряженности внешнего
электрического поля Е. Электроны в
проводнике будут перемещаться до
тех пор, пока напряженность
результирующего поля не станет
равной нулю (Е/ = Е – Е0 = 0, Е0=–Е0).
58
51

52.

Следовательно, при внесении
проводника в электрическое поле,
внутри проводника поле отсутствует,
и нет избыточных зарядов.
Таким образом, влияние вещества
на внешнее электрическое поле
приводит к возникновению
индуцированных зарядов в
веществе, создающие
дополнительное электрическое поле.
58
52

53.

Полное поле есть суперпозиция
электрических полей, возбуждённых
всеми первичными и
индуцированными зарядами.
Явление возникновения
индуцированных зарядов на
поверхности проводника во внешнем
электрическом поле называют
электростатической индукцией.
58
53

54.

Согласно (Е = grad ) отсутствие
поля внутри проводника означает,
что потенциал в проводнике
одинаков во всех его точках –
эквипотенциален.
58
54

55.

Следовательно, любой проводник в
электростатическом поле
представляет собой
эквипотенциальный объем, а его
поверхность является
эквипотенциальной.
Поэтому непосредственно у этой
поверхности вектор напряженности
электрического поля направлен по
нормали к ней в каждой ее точке.
58
55

56.

58
56

57.

С помощью теоремы Гаусса можно
доказать, что нормальная
составляющая напряженности
электрического поля на границе
проводник-вакуум определяется
следующим выражением:
σ
En
ε0
58
57

58.

Это выражение можно получить с
помощью теоремы Гаусса, с учётом
того, что всё поле направлено
наружу:
1
σS
E E Sn En S q
ε0
ε0
58
58

59.

58
59