Похожие презентации:
Электростатическое поле в вакууме. Принцип суперпозиции. Проводники в электростатическом поле
1. Занятие 1. Электростатическое поле в вакууме. Принцип суперпозиции. Проводники в электростатическом поле
МГТУ им.Н.Э. Баумана
∙ Напряжённость электростатического поля.
Принцип суперпозиции
∙ Теорема Гаусса в интегральной, дифференциальной формах
∙ Потенциал от системы дискретно и непрерывно распределённых
в пространстве неподвижных зарядов
∙ Метод изображений
∙ Ауд.: Иродов И.Е. Задачи по общей физике.- М.: Бином,
1998 2010. №№ 2.18, 2.27, 2.36, 2.69
2. Напряжённость электростатического поля. Принцип суперпозиции
МГТУ им.Н.Э. Баумана
Результирующий вектор Eр напряжённости электростатического поля в
вакууме от системы неподвижных точечных q1, q2 ,..., qn зарядов:
1 n qi ri (1)
,
Er
2
4 0 i 1 ri ri
где ri – вектор, направленный от i – го точечного qi заряда в
рассматриваемую точку пространства; ri /ri – единичный вектор для
ri вектора.
Вектор dE напряжённости электростатического поля в вакууме,
создаваемого в рассматриваемой точке пространства
1 dq r
элементарным dq зарядом: dE
(2)
2
4 0 r r
3.
МГТУ им.Н.Э. Баумана
Результирующий вектор Eр напряжённости электростатического поля в
вакууме в рассматриваемой точке пространства, создаваемого
непрерывно распределёнными в V объёме элементарными dq
зарядами и не находящимися в этой точке пространства:
1
dq r
Eр
, (3)
2
4 0 ( q ) r r
где r– вектор, направленный от элементарного dq заряда в точку
пространства, где вычисляется результирующий
вектор Eр напряжённости электростатического
поля в вакууме; r /r – единичный вектор для ri вектора.
4. Теорема Гаусса в интегральной, дифференциальной формах
dSn
S
+
- +
S
q+
ФE > 0
dS
E
Рис. 1
n
+ - E
q-
ФE < 0
Поток ФE результирующего Eр вектора напряжённости в вакууме
электростатического поля сквозь произвольную замкнутую
воображаемую поверхность S площадью, проведённую в
поле и охватывающую непрерывно распределённый в V
объёме q заряд, пропорционален интегралу по V объёму
с подинтегральной функцией, равной объёмной ρ = dq/dV
плотности этих q зарядов:
МГТУ им.
Н.Э. Баумана
5.
1ФE E р dS
(S )
0
n
qi
i 1
1
0
(4)
dV
МГТУ им.
Н.Э. Баумана
V
Дифференциальная форма теоремы Гаусса: дивергенция divEр
результирующего Eр вектора напряжённости в вакууме
электростатического поля, которое обозначается также ΔEр, численно
равен сумме приращений проекций на OX, OY, OZ координат Eр вектора
напряжённости на единице длины каждой из координат в
рассматриваемой точке некоторого объёма и пропорциональна
объёмной ρ = dq/dV плотности в рассматриваемой точке
некоторого объёма q зарядов:
E X EY EZ
E р divE р
. (5)
x
y
z 0
6. Потенциал от системы дискретно и непрерывно распределённых в пространстве неподвижных зарядов
МГТУ им.Н.Э. Баумана
Принцип суперпозиции: при наложении электростатических полей φj
потенциал в j – ой точке пространства является алгебраической суммой
от каждого одиночного qi заряда из системы n точечных q1, q2 ,..., qn
n
n
q
1
зарядов:
i
(6)
,
j
4 0
r
i 1
ij
i 1
ij
где rij – модули rij векторов, направленных от каждого qi заряда в эту j
– ую точку пространства.
1
dq
Для непрерывно распределённых зарядов: j 4 r , (7)
0 (q)
где r– модули r векторов, направленных от каждого
элементарного dq заряда в j – ую точке пространства, где
определяется φj потенциал.
7. Метод изображений
φ2 > φ 1+
q+
φ2
+
q+
φ2
-
-
- -
φ2 > φ1
φ1
φ1
φ=0
МГТУ им.
Н.Э. Баумана
φ=0
-
-φ1
Рис. 2
- q
-
-φ2
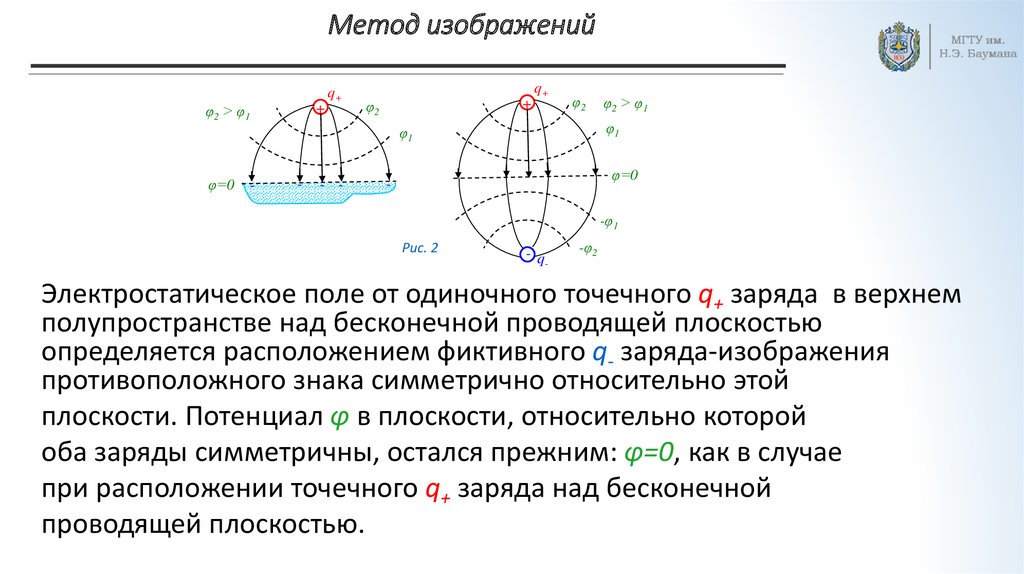
Электростатическое поле от одиночного точечного q+ заряда в верхнем
полупространстве над бесконечной проводящей плоскостью
определяется расположением фиктивного q- заряда-изображения
противоположного знака симметрично относительно этой
плоскости. Потенциал φ в плоскости, относительно которой
оба заряды симметричны, остался прежним: φ=0, как в случае
при расположении точечного q+ заряда над бесконечной
проводящей плоскостью.
8. Задача № 2.18
МГТУ им.Н.Э. Баумана
Задача № 2.18
Находящийся в вакууме тонкий прямой стержень 2а длиной заряжен
равномерно q зарядом.
Найти модуль напряжённости электрического поля как функцию r
расстояния от центра стержня до точки прямой, а) перпендикулярной
стержню и проходящей через его центр; б) совпадающей с осью
стержня, если r > a. Исследовать выражения при r >> a.
q
.
Ответ: а) E
б)
;
2
2
4 0 ( r a )
4 0 r r 2 a 2
q
В обоих случаях при r>>a напряжённость E 4 r 2 .
0
q
E
9. Решение:
а) Дано: 2а,q, r/ EM(r)=?МГТУ им.
Н.Э. Баумана
2a
dy(dq)
dy(dq)
O
j
α
A
i
r
rM
rMA
rMB
M
dEMB
α
α
dEMA
dEMA + dEMB
X
Рис.3
B
Y
10.
МГТУ им.Н.Э. Баумана
Вектор напряжённости электростатического поля в плоскости,
перпендикулярной оси стержня и проходящей через его центр,
сонаправлен rM радиусу-вектору, а величина его E модуля постоянна,
поэтому достаточно определить E модуль в M точке. Векторы dEMA, dEMB в
M точке от симметрично расположенных в т.т. A, B элементарных dq =
(q/2a)dy зарядов, где q/2a - линейная плотность зарядов на стержне:
dq
rMA
dq
rMB
dEMA
(
); dEMB
(
). (8)
2
2
4 0 rMA rMA
4 0 rMB rMB
11.
МГТУ им.Н.Э. Баумана
Согласно принципу суперпозиции результирующий вектор dEMр
напряженности электростатического поля, направленный по OX оси, в
M точке на боковой поверхности цилиндра r радиусом с учётом r2 MA =
= r2 MB = y2 + r2; dq = (q/2a)dy :
dEMр dEMA dEMB
qdy
8a 0 ( y r )
2
2
3
2
(rMA rMB )
i , (9)
qrdy
4a 0 ( y r )
2
2
3
2
где r MA + r MB = 2ri - сумма двух векторов, а i – единичный
вектор OX оси;
12.
МГТУ им.Н.Э. Баумана
dEMр
qrdy
4a 0 ( y r )
2
2
3
2
модуль вектора dEMр напряженности
электростатического поля.
Согласно принципу суперпозиции EMр модуль результирующего вектора
EMр напряженности электростатического поля, направленный по OX оси,
от всех симметрично расположенных относительно этой OX оси
элементарных зарядов:
E Mр
dE Mр
(q)
qr
4a 0
q
4 0 r
a
2
r
2
.
a
0
dy
(y2 r2 )
3
2
(10)
13.
МГТУ им.Н.Э. Баумана
При r >> a модуль EMр результирующего вектора EMр напряженности
электростатического поля:
q
E Mр
. (11)
2
4 0 r
б) Дано: 2а,q, r/ EM(r)=?
2a
dy(dq)
A
rMA
O
j
i
dEMA
r
a+r-y
a+r
X
M
Рис.4
Y
14.
МГТУ им.Н.Э. Баумана
Модуль dEMA вектора dEMA в M точке от расположенного в т. A
элементарного dq = (q/2a)dy заряда, где q/2a - линейная плотность
qdy
зарядов на стержне:
(12)
dE M
.
2
8a 0 (a r y )
Согласно принципу суперпозиции EM модуль вектора EM напряженности
электростатического поля, направленный по OY оси, от всех
элементарных зарядов на стержне:
2a
q
dy
q
(13)
E M dE M
.
2
2
2
8
a
(
a
r
y
)
4
(
r
a
)
0 0
0
(q)
При r >> a модуль EM вектора EM напряженности
q
электростатического поля:
E Mр
. (14)
2
4 0 r
15. Задача №2.27
МГТУ им.Н.Э. Баумана
Бесконечно длинная круглая цилиндрическая поверхность заряжена
равномерно в вакууме по длине с поверхностной плотностью
σ = σ0 cosφ, где φ - полярный угол цилиндрической системы координат,
ось OZ которой совпадает с осью данной поверхности. Найти
E модуль и направление E вектора напряжённости электростатического
поля на оси OZ.
Ответ:
0
E
,
2 0
вектор E направлен под углом φ = π.
16. Решение:
-Дано: σ=σ0cosφ/EOZ=?
МГТУ им.
Н.Э. Баумана
-
-
-
-ρ
-
E = E1 + E2
-
E1
E2
r2
a
a
r1
M
Y
Y
π
+
φ
+
+
+
+
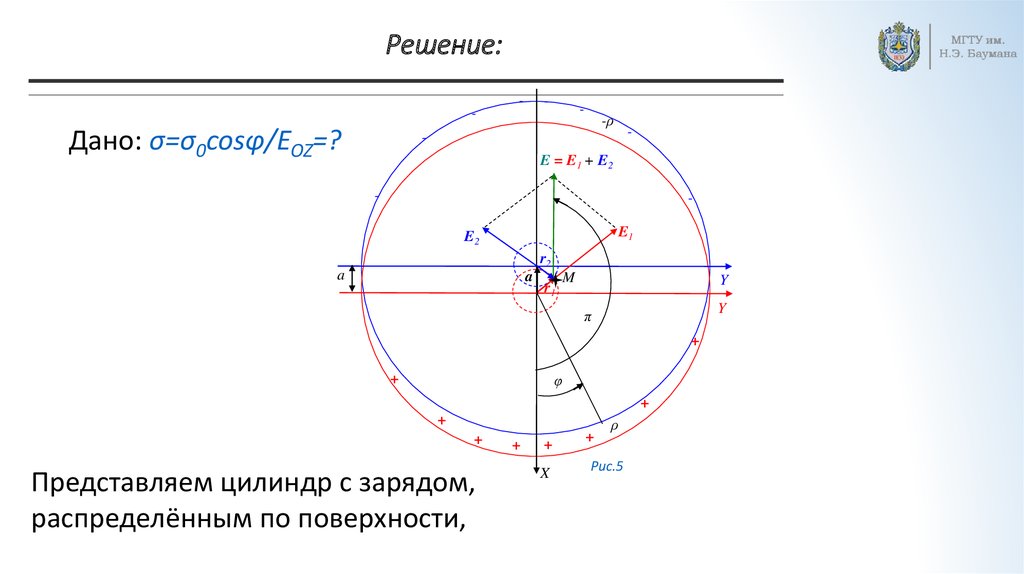
Представляем цилиндр с зарядом,
распределённым по поверхности,
+
+
X
+
ρ
Рис.5
17.
МГТУ им.Н.Э. Баумана
двумя одинаковыми цилиндрами с положительным и отрицательным
зарядами с ρ и -ρ объёмными плотностями, наложенными друг на друга
с малым смещением их центров на длину a вектора. Тогда в
пересечении этих цилиндров заряд отсутствует, а его поверхностная
плотность заряда соответствует заданной.Согласно теореме Гаусса
модули E1, E2 векторов E1, E2 на боковой поверхности в M точке каждого
заряженного цилиндров r1, r2 радиусами:
1
r1, 2 2
r1, 2
(15)
E
d
S
dV
E
2
r
H
H
E
,
1
,
2
1
,
2
1
,
2
1
,
2
0
2 0
0 V
(S )
где H – высота цилиндра.
Вследствие отрицательного заряда, охватываемого боковой
поверхностью цилиндра r2 радиусом, E2 вектор направлен
18.
r1r2 (16)
; E2
.
противоположно r2 радиусу-вектору: E1
2 0
2 0
Вектор E = E1 + E2 напряжённости электростатического поля в M точке,
находящейся на оси OZ бесконечно длинного цилиндра, как
суперпозиция векторов E1, E2 от каждого заряженного цилиндра
r1 ,r2
a
радиусами:
E E1 E2 (r1 r2 ) ,
(17)
2 0
2 0
где r1 – r2 = a.
Вектор E сонаправлен a вектору и составляет π угол с OX осью.
Поверхностную плотность σ0 заряда бесконечно длинного цилиндра при
φ = 0 нормируем: σ0 = ρa.Тогда E модуль вектора E на оси
OZ бесконечно длинного заряженного цилиндра:
0
E
. (18)
2 0
МГТУ им.
Н.Э. Баумана
19. Задача № 2.36
МГТУ им.Н.Э. Баумана
Имеются два тонких проволочных кольца R радиуса
каждое, оси которых совпадают. Заряды колец равны
q и –q. Найти разность потенциалов между центрами колец, отстоящими
друг от друга на расстоянии l, если R = 30 см, l = 52 см и q = 0,40 мкКл.
Ответ:
1
1
1 ( l )2
R
2 0 R
q
12кВ.
20.
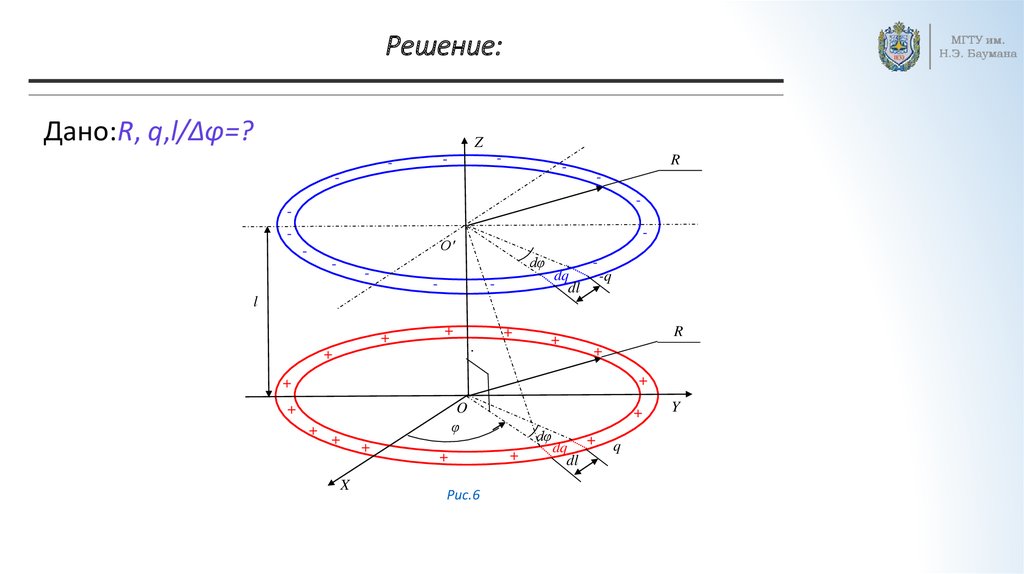
Решение:Дано:R, q,l/Δφ=?
МГТУ им.
Н.Э. Баумана
Z
-
-
-
R
-
-
-
-
-
-
O′
-
-
dφ
-
dq
dl
-
-
-q
l
+
+
+
.
+
+
R
+
+
+
O
φ
+
+
+
+
X
+
Рис.6
+
dφ
+
dq
dl
+
q
Y
21.
МГТУ им.Н.Э. Баумана
Положительный q заряд распределён равномерно по окружности 2πR
q
длиной, поэтому τ линейная плотность этого заряда:
.
(19)
2 R
Элементарный dq заряд на длине dl = Rdφ кольца: dq dl qd .
2
(20)
Потенциал dφ0+ в т.O от элементарного положительного dq заряда,
находящегося на расстоянии R от центра кольца:
dq
qd
d 0
4 0 R
8 0 R
2
.
(21)
Согласно принципу суперпозиции суммарный потенциал φΣO+ в т.O от
элементарных положительных зарядов:
0
2
q
q
d 0 2
d
(22)
4 0 R
8 0 R 0
(q)
22.
МГТУ им.Н.Э. Баумана
Согласно принципу суперпозиции суммарный потенциал φΣO - в т.O от
элементарных отрицательных зарядов:
2
q
q
O d 0
d
. (23)
2
2
2
2
2
(q)
8 0 R l
0
4 0 R l
Суммарный потенциал φΣO в т.O от элементарных положительных и
отрицательных зарядов:
1
0 O O
1
l )2
1
(
q
q
R
4 0 R 4 0 R 2 l 2
4 0 R
Суммарный потенциал φΣO′ в т.O′ от элементарных
отрицательных и положительных зарядов:
q
.
(24)
23.
МГТУ им.Н.Э. Баумана
0 O O
1
1
l )2
1
(
q
q
R
2
2
4 0 R 4 0 R l
4 0 R
Разность Δφ потенциалов между центрами колец т.т.O,O′:
0 0
1
1
1 ( l )2
R
2 0 R
q
1
1
4 10 7
1 (0,52
) 2
0,30
2 3,14 8,85 10 12 0,30
Кл
12кВ.
Ф м
м
(26)
q
.
(25)
24. Задача №2.69
Тонкое проволочное кольцо R = 7,5 см радиуса имеетq = 5,2 мкКл заряд. Кольцо расположено параллельно проводящей
плоскости на l = 6,0 см расстоянии от неё. Найти σ поверхностную
плотность заряда в точке плоскости, расположенной симметрично
относительно кольца.
Ответ:
ql
2 (l R )
2
2
3
2
мкКл
56 2
м
МГТУ им.
Н.Э. Баумана
25. Решение:
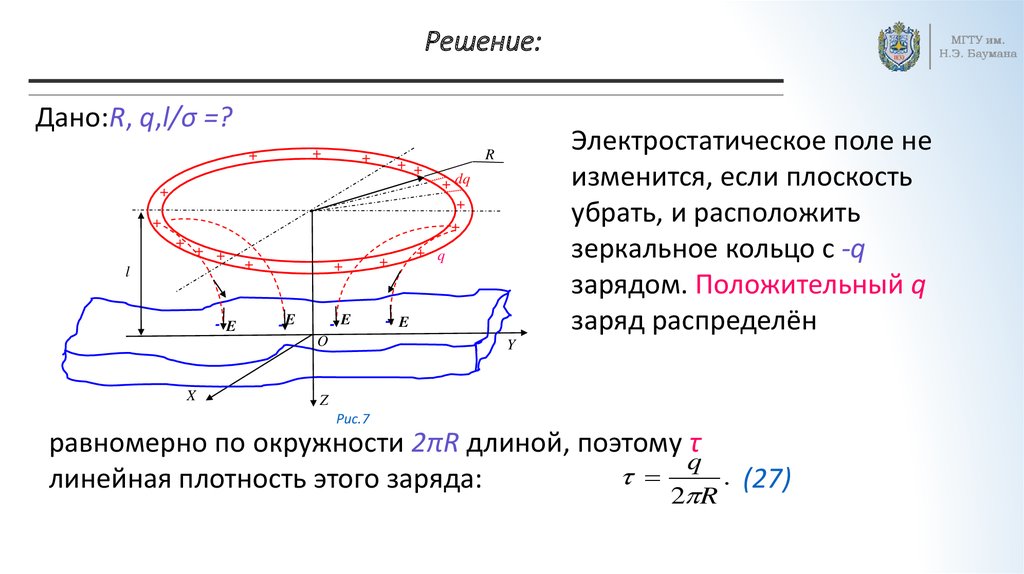
Дано:R, q,l/σ =?+
+
+
+ +
+
Электростатическое поле не
изменится, если плоскость
убрать, и расположить
зеркальное кольцо с -q
зарядом. Положительный q
заряд распределён
R
+ dq
+
+
+
+
+ +
l
-E
+
+
-E
-E
O
X
+
МГТУ им.
Н.Э. Баумана
+ q
- E
Y
Z
Рис.7
равномерно по окружности 2πR длиной, поэтому τ
q
. (27)
линейная плотность этого заряда:
2 R
26.
++
R
+
+
+
dq
υ
φ
dφ
+++
+
l
+
q
+
+
МГТУ им.
Н.Э. Баумана
+ +
+
dl
dφ dq
+
r
O idEX
- jdEY
l
i
k j
υ
kdEZ
-
-
-
Y
dφ
-
X
dE
dq dφ
dl
- -
dq
-
-
-
-
-q
R
Z
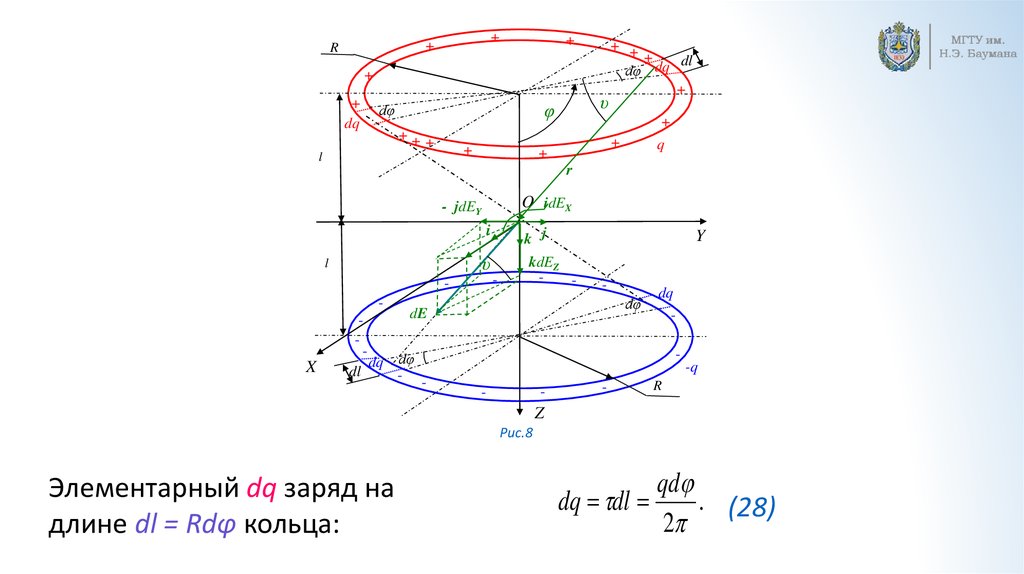
Рис.8
Элементарный dq заряд на
длине dl = Rdφ кольца:
qd
dq dl
. (28)
2
27.
Вектор dE напряжённости электростатического поля в т.O отэлементарного положительного dq заряда, находящегося
на расстоянии R 2 l 2 от центра кольца:
dq
r
qd
dE
4 0
R l r
2
2
8 0
2
МГТУ им.
Н.Э. Баумана
r
.
2
2 r
R l
(29)
Составляющая вектора kdEZ по OZ оси в т.O от элементарного
l
положительного dq заряда c учётом sin 2 2 угла ν, под которым r
R l
радиус-вектор направлен в т.O :
k dE Z k
dq
4 0 R l
2
2
sin k
Другие составляющие dE вектора напряжённости
электростатического поля от элементарного
положительного dq заряда можно не учитывать,
qld
8 2 0 ( R 2 l 2 )
3
. (30)
2
28.
МГТУ им.Н.Э. Баумана
поскольку каждому элементарному заряду соответствует
симметричный заряд относительно O точки, составляющие dE
вектора idEX по OX оси и jdEY по OY оси которого равны по модулю и
противоположны по направлению.
Согласно принципу суперпозиции суммарная проекция EZ на OZ ось
dE вектора напряжённости электростатического поля в т.O от всех
элементарных положительных зарядов на кольце:
EZ dEZ
(q)
2
ql
8 0 ( R l )
2
2
2
3
d
2 0
ql
4 0 ( R l )
2
Согласно принципу суперпозиции суммарная проекция EZΣ
на OZ ось EZΣ вектора напряжённости электростатического
поля в т.O от всех элементарных положительных
2
3
.
2
(31)
29.
и отрицательных зарядов на действительном и зеркальномкольце:
ql
EZ
2 0 ( R l )
2
2
3
.
2
МГТУ им.
Н.Э. Баумана
(32)
Вектор EZΣ напряжённости электростатического поля в т.O - это
напряжённость электростатического поля в точке проводящей
плоскости, расположенной симметрично относительно кольца и
имеющей одну составляющую вектора kEZΣ по OZ оси. Поэтому
поверхностная плотность σ заряда в точке плоскости, расположенной
симметрично относительно кольца:
ql
5,2 10 6 0,06
Кл м
мкКл
(33)
0 EZ
56
3
3
3
2 .
2 ( R 2 l 2 )
2
2 3,14 (0,075 2 0,06 2 )
2
м
Дома: Иродов И.Е. Задачи по общей физике.М.: Бином, 1998 2010. №№ 2.17, 2.44
Спасибо за внимание!
м
























 Физика
Физика








