Уравнение Пуассона. Электростатическое поле в вакууме

1.

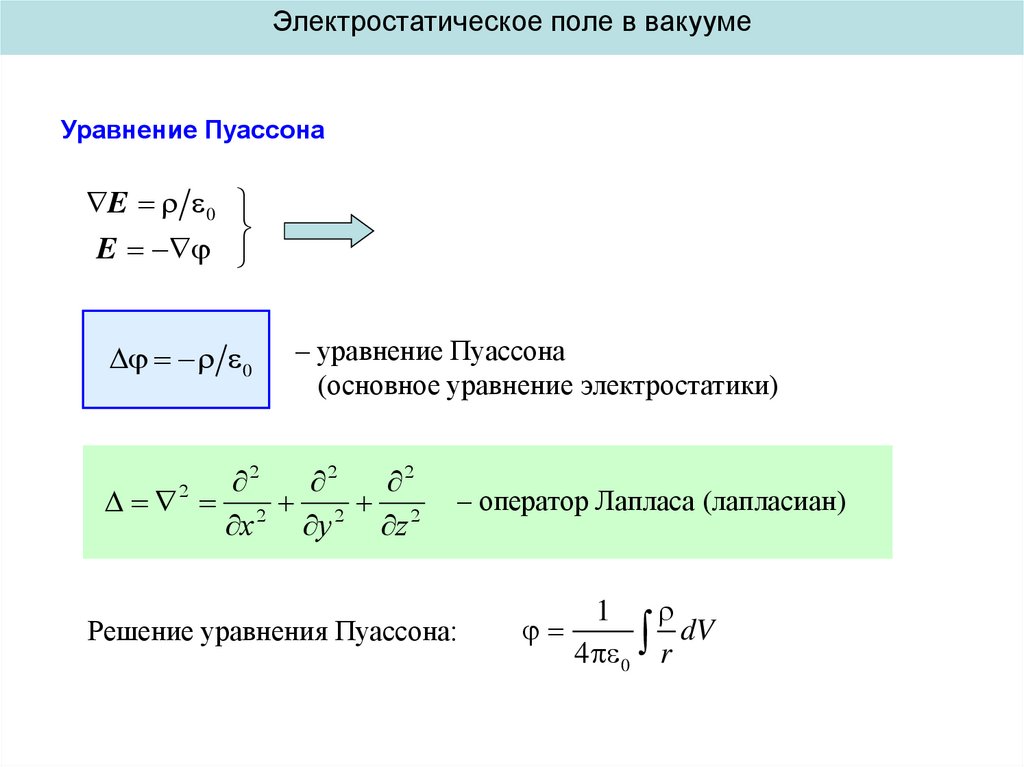
Электростатическое поле в вакууме
Уравнение Пуассона
E 0
E
0
– уравнение Пуассона
(основное уравнение электростатики)
2
2
2
2 2 2 2
x
y
z
– оператор Лапласа (лапласиан)
Решение уравнения Пуассона:
1
dV
4 0 r

2.

Электростатическое поле в вакууме
Уравнение Пуассона
Частный случай
0
– уравнение Лапласа
0
Проводник
0
1
1
Проводник
2
2

3.

Электростатическое поле в вакууме
Свойства потенциала
A12 – работа по перемещению q
1)
2
2
2
1
1
A12 Fdr q Edr q ( 1 2 )
q
A12 q ( 1 2 )
1
С другой стороны
A12 U1 U 2 , где U – потенциальная энергия
U q

4.

Электростатическое поле в вакууме
Свойства потенциала
2)
Вычисление потенциала
1
dV
4 0 r
– 1 интеграл
Вычисление напряженности
1
r
E
dV
3
4 0 r
Из
– 3 интеграла
E

5.

Электростатическое поле в вакууме
Геометрическое описание электрического поля
Для изображения электрического поля используются:
1) Силовые линии (СЛ)
E
Силовая линия – кривая, в каждой точке
которой касательный вектор совпадает по
направлению с вектором E.
Уравнение силовой линии :
СЛ
dx dy dz ds
Ex E y Ez E
s – длина силовой линии

6.

Электростатическое поле в вакууме
Геометрическое описание электрического поля
2) Эквипотенциальные поверхности (ЭП)
Эквипотенциальные поверхности – поверхности,
все точки которых имеют одинаковый потенциал.
Уравнение эквипотенциальной поверхности:
ЭП
( x, y, z ) 0

7.

Электростатическое поле в вакууме
Геометрическое описание электрического поля
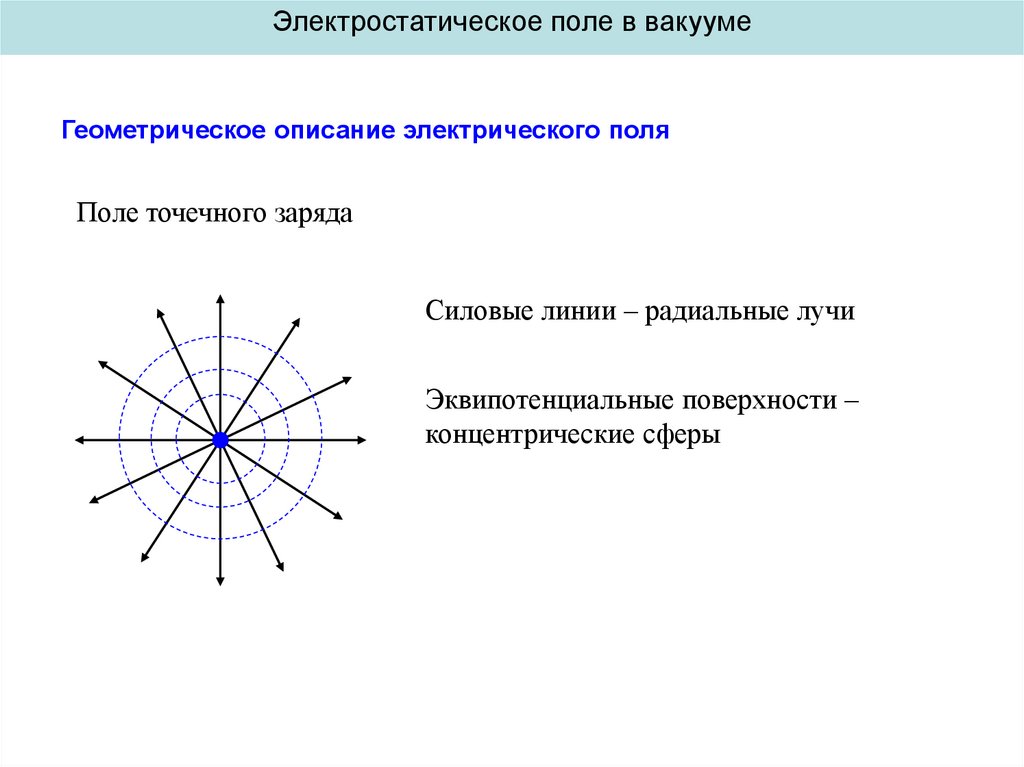
Поле точечного заряда
Силовые линии – радиальные лучи
Эквипотенциальные поверхности –
концентрические сферы

8.

Электростатическое поле в вакууме
Геометрическое описание электрического поля
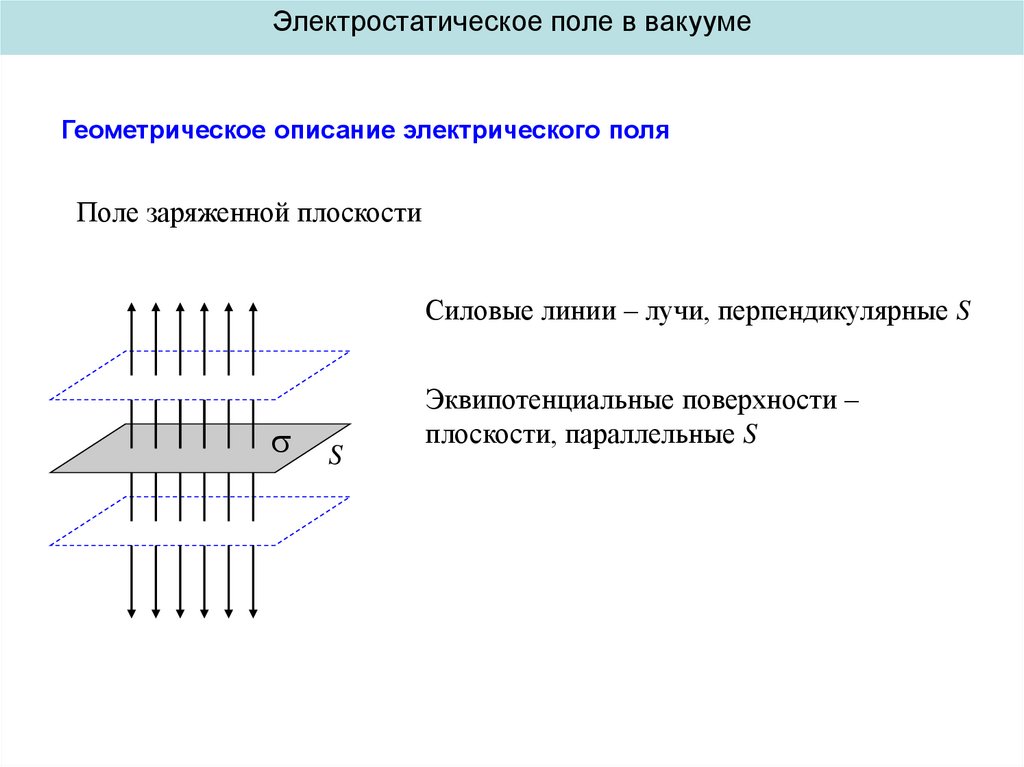
Поле заряженной плоскости
Силовые линии – лучи, перпендикулярные S
S
Эквипотенциальные поверхности –
плоскости, параллельные S

9.

Электростатическое поле в вакууме
Геометрическое описание электрического поля
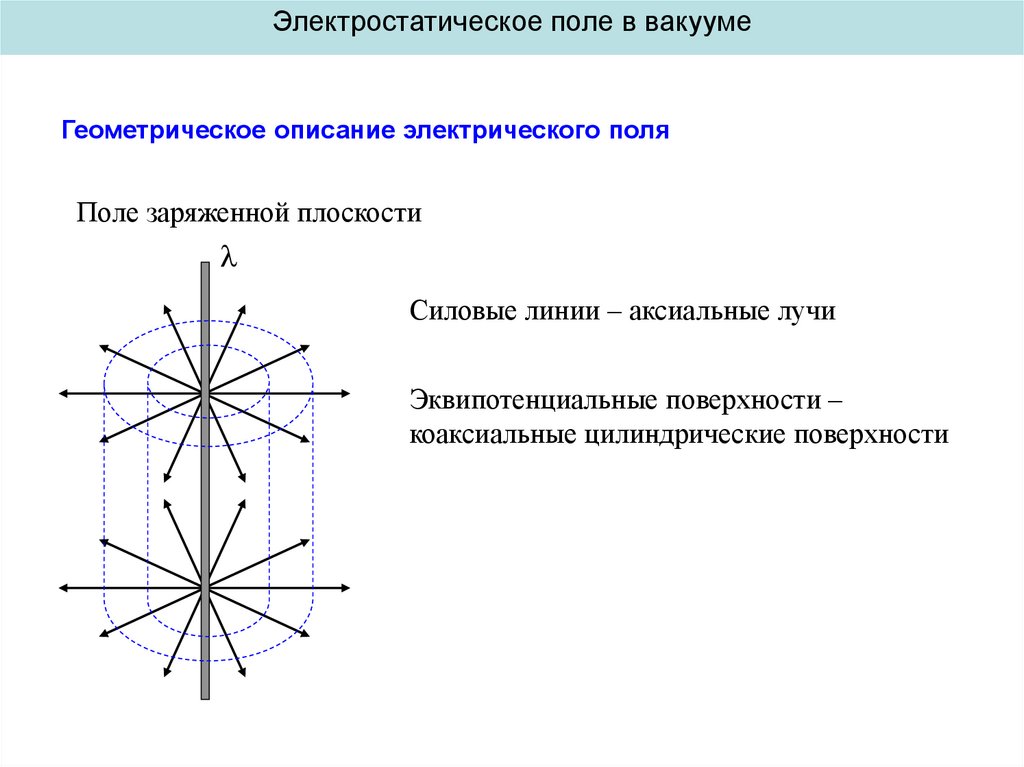
Поле заряженной плоскости
Силовые линии – аксиальные лучи
Эквипотенциальные поверхности –
коаксиальные цилиндрические поверхности

10.

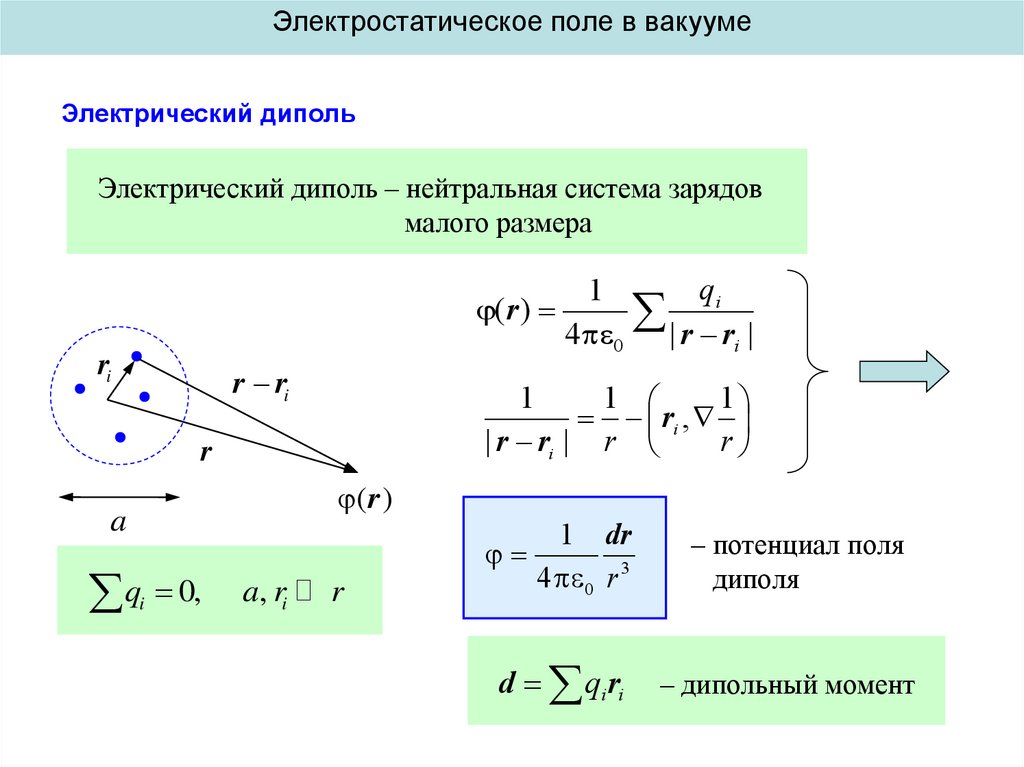
Электростатическое поле в вакууме
Электрический диполь
Электрический диполь – нейтральная система зарядов
малого размера
qi
1
( r )
4 0 | r ri |
ri
r ri
1
1
1
ri ,
| r ri | r
r
r
( r )
a
q 0,
i
a, ri
r
1 dr
4 0 r 3
d qi ri
– потенциал поля
диполя
– дипольный момент

11.

Электростатическое поле в вакууме
Электрический диполь
Пример диполя
Напряженность поля диполя:
l
q
q
d ql
E
E
1
4 0
d 3(dr )r
r 3 r 5
Сила, действующая на диполь:
F qi E (ri )
d
x
F Fx d
F (d ) E
E x
x
диполь втягивается
в поле

12.

Электростатическое поле в вакууме
Электрический диполь
Момент сил, действующий на диполь:
M [ri , qi E (ri )]
M d E
d
E
Энергия “жесткого ” диполя в поле: d const
U qi (ri )
U d E

13.

Электростатическое поле в вакууме
Энергия электрического поля
j
qi
qj
Энергия взаимодействия двух точечных зарядов:
1 qi
Uij q j j , j
4 0 rij
1 qi q j
U ij
4 0 rij
Энергия взаимодействия системы зарядов:
U U ij
i j
1
U ij
2 i j
1
1 qi q j 1
U
qi i
2 i j 4 0 rij
2 i

14.

Электростатическое поле в вакууме
Энергия электрического поля
Энергия взаимодействия системы зарядов:
дискретное распределение:
U
1
qi i
2 i
объемное распределение:
U
1
dV
2
0 E 2
U
dV
2
0 E 2
u
2
– плотность энергии
электрического поля

15.

Проводник в электростатическом поле
Влияние вещества на поле
Eвн 0
Eвн
Электростатическая индукция –
смещение зарядов вещества
под воздействием внешнего
поля и появление
индуцированных зарядов
E Eвн Eинд – результирующее поле
Eвн
– внешнее поле (внешних зарядов)
Eинд – поле индуцированных зарядов

16.

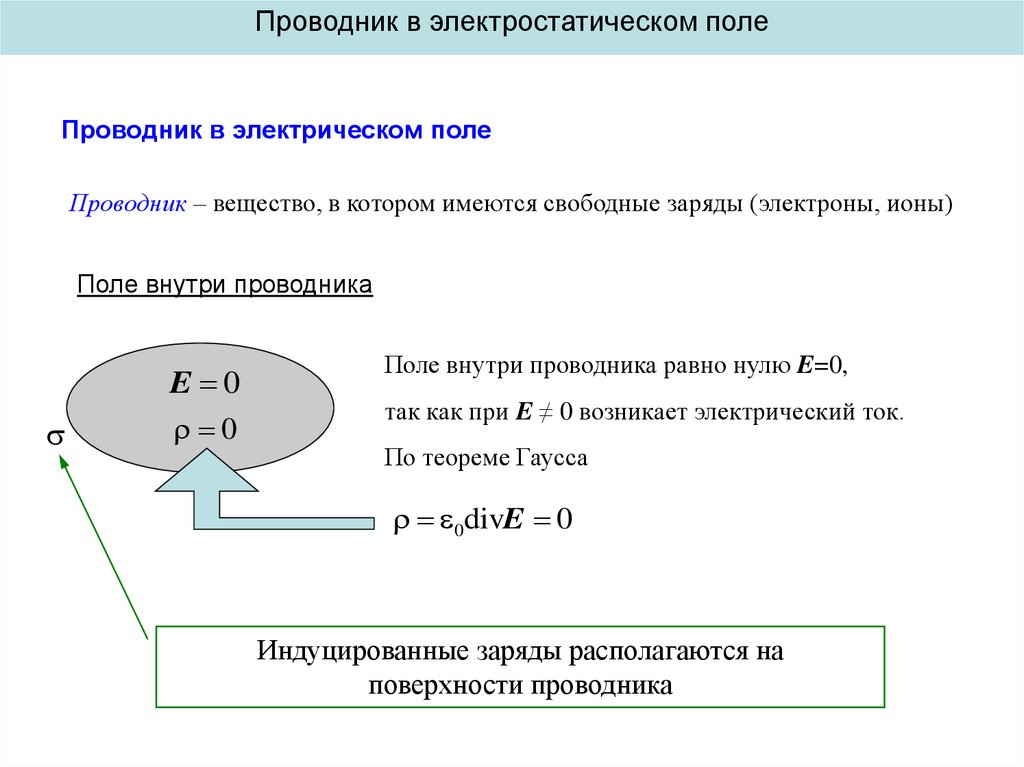
Проводник в электростатическом поле
Проводник в электрическом поле
Проводник – вещество, в котором имеются свободные заряды (электроны, ионы)
Поле внутри проводника
E 0
0
Поле внутри проводника равно нулю E=0,
так как при E ≠ 0 возникает электрический ток.
По теореме Гаусса
0divE 0
Индуцированные заряды располагаются на
поверхности проводника

17.

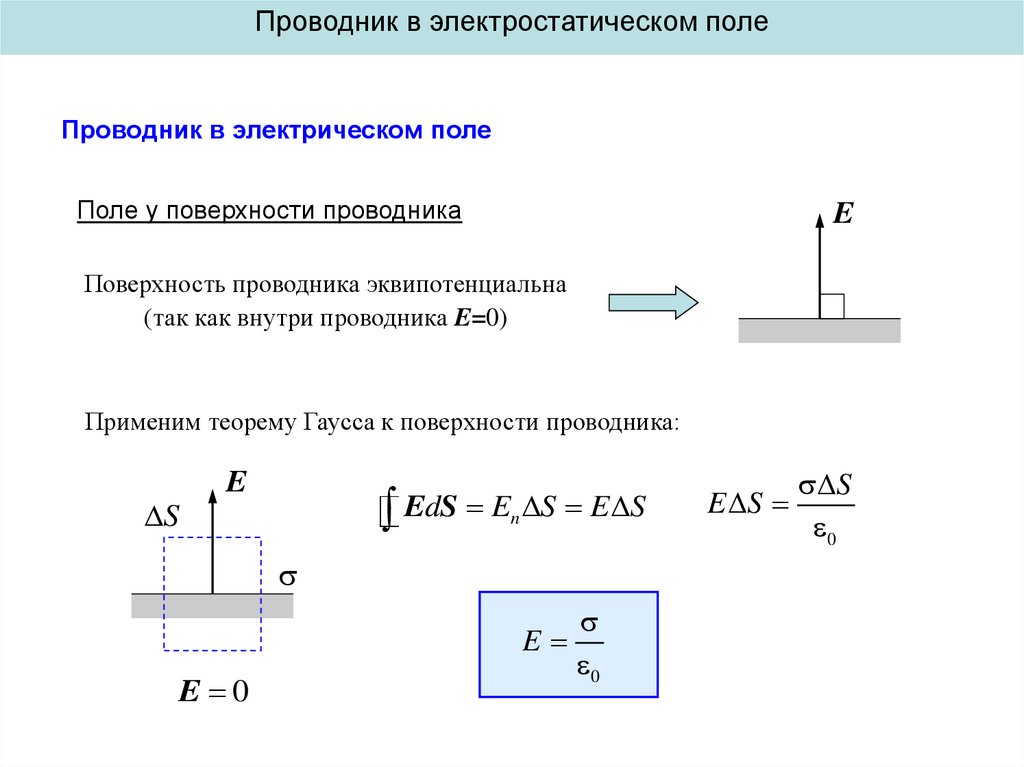
Проводник в электростатическом поле
Проводник в электрическом поле
Поле у поверхности проводника
E
Поверхность проводника эквипотенциальна
(так как внутри проводника E=0)
Применим теорему Гаусса к поверхности проводника:
S
E
EdS E S E S
n
E 0
E
0
S
E S
0

18.

Проводник в электростатическом поле
Проводник в электрическом поле
Поверхностная сила, действующая на проводник
x
dF
dS
dF
Edx
dS
( x )
dx
dS
По теореме Гаусса
dE
dx 0
E
dF
dE
0
E dx 0 EdE
dS
dx
0
dF 0 E 2 E
dS
2
2