Похожие презентации:
Проводники в электрическом поле. Лекция3
1. Лекция № 3 ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
731
2. 9. Распределение зарядов в проводнике. Общая задача электростатики.
732
3. 10. Конденсаторы. Электроёмкость конденсаторов плоского, сферического, цилиндрического. Соединение конденсаторов параллельное и
последовательное.11. Ёмкостные коэффициенты.
Энергия заряженного конденсатора.
Объёмная плотность электрической
энергии. Сила взаимодействия
обкладок конденсатора.
73
3
4. 9. Распределение зарядов в проводнике. Общая задача электростатики.
734
5. Если телу сообщить избыточный заряд q, то он распределится так, чтобы соблюдалось равновесие. Это означает, поток вектора
электрической напряжённости черезлюбую замкнутую поверхность
внутри проводника равен нулю, то
есть, весь заряд распределился по
поверхности проводника внутри
проводника не может быть никаких
зарядов.
73
5
6. Даже если удалить полость внутри проводника, это никаким образом не повлияет на электростатическое поле, так как все заряды
находятсяснаружи.
73
6
7. Рассмотрим потенциал φ и поверхностную плотность заряда σ для шара (R – радиус шара):
1 qφ
q 4 πε 0 Rφ
4 πε 0 R
q
q
1
1
σ
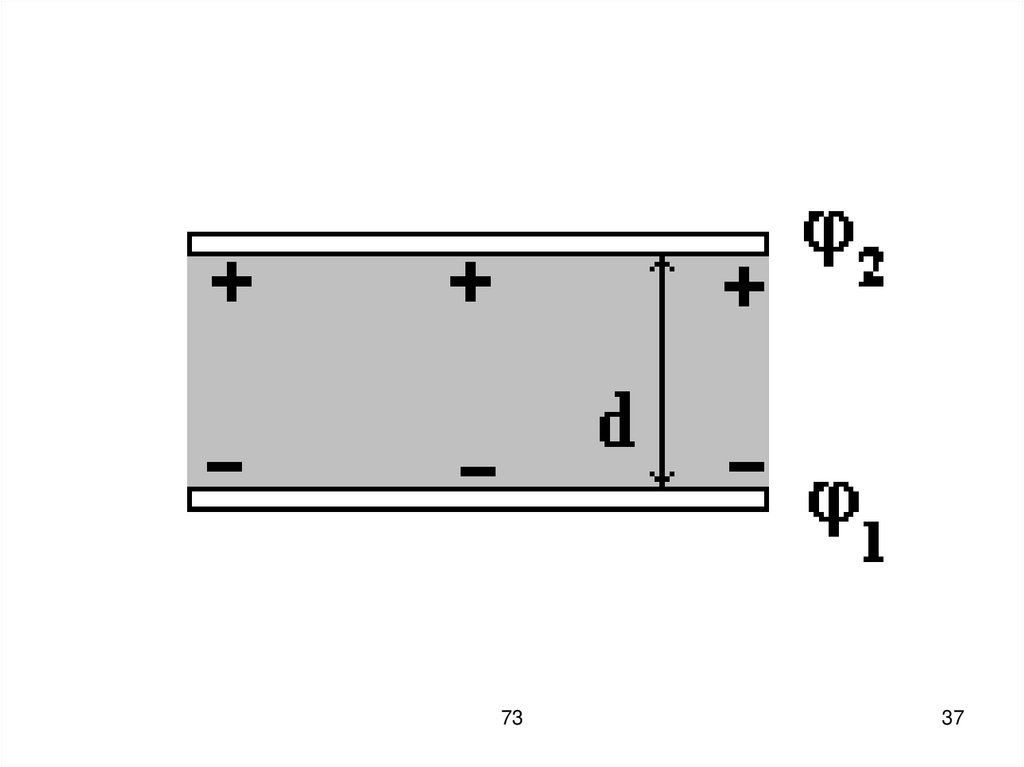
ε 0φ σ ~
2
S 4πR
R
R
73
7
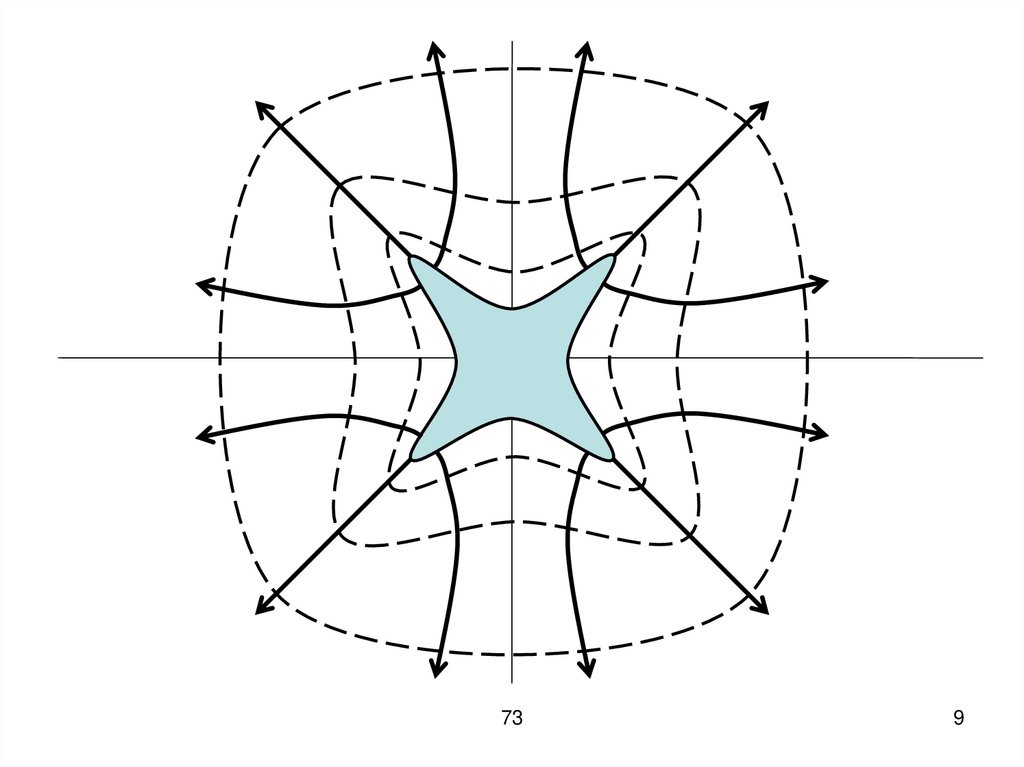
8. То есть, чем «острее» данный участок проводника, тем больше на нём скапливается зарядов. Этот вывод соответствует минимуму
энергии: чем дальше заряды друг отдруга, тем меньше сила
взаимодействия и меньше
потенциальная энергия.
73
8
9.
739
10. Большей плотности поверхностного заряда соответствует большая напряжённость поля и большее число силовых линий. Вблизи
проводникаэквипотенциальные линии
повторяют поверхность тела.
73
10
11. Чем дальше от проводника, тем больше они напоминают сферу, то есть с ростом расстояния поле всё больше походит на поле от
точечного заряда.73
11
12. Общая задача электростатики. Уравнения Пуассона и Лапласа.
7312
13. В диэлектрическое среде заданы расположение и форма всех проводников. Известна диэлектрическая проницаемость среды ε между
проводниками и объёмная плотностьсвободных электрических зарядов во
всех точках диэлектриков.
73
13
14. Кроме того, известны: а) либо потенциалы всех проводников; б) либо заряды всех проводников; в) либо заряды некоторых
проводников и потенциалы всехостальных проводников.
73
14
15. Требуется определить напряжённость электрического поля во всех точках пространства по поверхностям проводников.
7315
16. Задача сводится к нахождению потенциала φ как функции пространственных координат (x, y, z). Найдём дифференциальное уравнение,
которому должнаудовлетворять эта функция.
73
16
17. Берём теорему Гаусса
ρdiv εE ,
ε0
ρ
div ε gradφ
ε0
73
17
18. Если диэлектрик однороден (ε не зависит от координат), то
ρdiv gradφ
ε 0ε
73
18
19. Или уравнение Пуассона оператор Лапласа
Или уравнение Пуассонаρ
φ
ε 0ε
оператор Лапласа
2 2 2
x y z
2
2
2
2
73
19
20. Если нет свободных зарядов, то получаем уравнение Лапласа: Решение дифференциального уравнения единственное.
Если нет свободных зарядов, тополучаем уравнение Лапласа:
φ 0
Решение дифференциального
уравнения единственное.
73
20
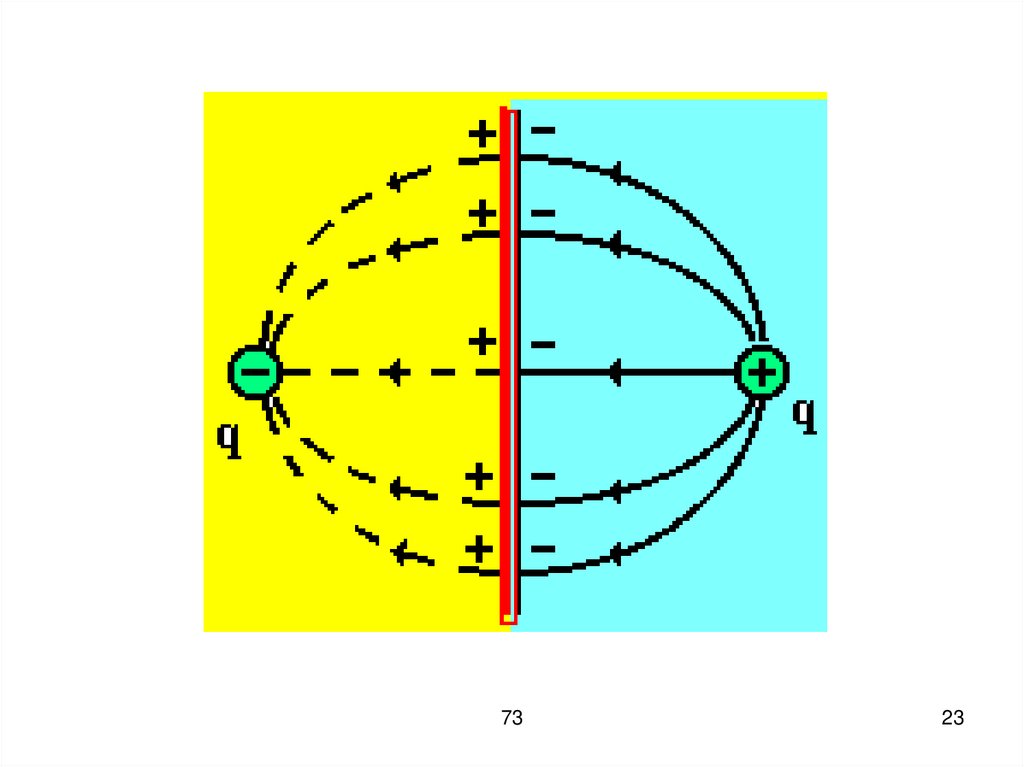
21. Зеркальное изображение электрических полей Пусть положительный точечный заряд +q находится на расстоянии r от безграничной
проводящейнезаряженной плоскости.
73
21
22. Этот заряд индуцирует на бесконечной проводящей плоскости заряд противоположного знака, где сплошными линиями показаны линии
напряженности электростатическогополя.
Сама проводящая плоскость
является эквипотенциальной с = 0.
73
22
23.
7323
24. Метод электрического (зеркального) изображения основан на том, что замена любой эквипотенциальной поверхности электрического
полябесконечной проводящей плоскости
с тем же потенциалом не вызывает
изменения этого поля.
73
24
25. Если на расстоянии, равном расстоянию заряда +q, от плоскости слева поместить «фиктивный» отрицательный точечный заряд q*= q
Если на расстоянии, равномрасстоянию заряда +q, от плоскости
слева поместить «фиктивный»
отрицательный точечный заряд
q*= q [он является «зеркальным»
отражением заряда +q относительно
плоскости], то картина линий
напряженности слева от плоскости
зеркально совпадет с линиями
напряженности действительного
электрического поля справа.
73
25
26. В этом случае вектор напряженности результирующего поля зарядов +q и q во всех точках плоскости будет перпендикулярен ей
В этом случае вектор напряженностирезультирующего поля зарядов +q и
q во всех точках плоскости будет
перпендикулярен ей (картина линий
напряженности точно такая же, как и
для электрического поля, созданного
системой двух равных по величине,
но противоположных по знаку
точечных зарядов).
73
26
27. Следовательно, электрическое поле справа от плоскости определяется только зарядами +q и q. Сила притяжения заряда +q к
Следовательно, электрическое полесправа от плоскости определяется
только зарядами +q и q.
Сила притяжения заряда +q к
проводящей плоскости равна
кулоновской силе, которая действует
между зарядами +q и q по закону
Кулона, ( q зеркальное
изображение заряда +q).
Где расстояние между зарядами
равно удвоенному расстоянию 2r.
73
27
28.
7328
29. 10. Конденсаторы. Электроёмкость конденсаторов плоского, сферического, цилиндрического. Соединение конденсаторов параллельное и
последовательное.73
29
30. Рассмотрим проводник, изолированный от влияния других проводников и заряженных тел. При сообщении заряда q проводнику возникает
потенциал ,пропорциональный этому заряду
( q).
73
30
31. Опыт показывает, что отношение заряда проводника к его потенциалу не зависит ни от заряда, ни от потенциала, является для
данногопроводника величиной постоянной,
которую называют электрической
ёмкостью проводника С (ёмкостью),
т.е.
С = q / .
73
31
32. Найдем ёмкость проводящего шара радиуса R. Потенциал на поверхности заряженного шара можно найти следующим образом (φ∞ = 0, Δφ
Найдем ёмкость проводящего шарарадиуса R. Потенциал на
поверхности заряженного шара
можно найти следующим образом
φ φ R E d Er dr
R
R
q
q
dr
2
4π ε 0 εr
4π ε 0 εR
R
(φ∞ = 0, Δφ = φ∞ – φR)
73
32
33. Отсюда, ёмкость металлического шара или сферы: С = q/φ =40R, где – диэлектрическая проницаемость окружающей среды, R –
Отсюда, ёмкость металлическогошара или сферы:
С = q/φ =4 0 R, где –
диэлектрическая проницаемость
окружающей среды, R – радиус
шара.
Следовательно, ёмкость проводника
зависит только от размеров и
формы, диэлектрической
проницаемости окружающей среды и
наличия вблизи других проводников.
73
33
34. В СИ емкость измеряют в Фарадах. Например, электроемкость Земного шара – С 0,7 мкФ.
В СИ емкость измеряют в Фарадах.Например, электроемкость Земного
шара – С 0,7 мкФ.
73
34
35. Если вблизи заряженного проводника находятся другие проводники, то ёмкость его будет увеличиваться, так как электрическое поле
вызываетпоявление на других проводниках
индуцированных зарядов.
73
35
36. Например, если заряд проводника положительный, то отрицательные индуцированные заряды на других телах располагаются ближе к
проводнику, что приведет куменьшению потенциала данного
проводника, а ёмкость увеличится.
73
36
37.
7337
38. Систему двух разноименно заряженных плоскостей (обкладок) называют плоским конденсатором. Их заряды равны по абсолютной
величине ( + q = – q = q).73
38
39. Если расстояние между обкладками много меньше их размеров, то электрическое поле является практически однородным и
сосредоточено между обкладками.Вне конденсатора поле практически
равно нулю.
73
39
40. Основной характеристикой конденсатора является электрическая емкость C = q / , где – разность потенциалов между его
Основной характеристикойконденсатора является
электрическая емкость
C = q / ,
где – разность потенциалов
между его обкладками.
73
40
41. Напряженность электрического поля между его обкладками Е = σ / ε0 ε, где q = S, – поверхностная плотность заряда на
Напряженность электрического полямежду его обкладками
Е = σ / ε0 ε,
где q = S, – поверхностная
плотность заряда на обкладках
конденсатора;
S – площадь его обкладок.
73
41
42. Используя связь напряженности с разностью потенциалов, в виде = Е d, получим d – расстояние между обкладками конденсатора,
Используя связь напряженности сразностью потенциалов, в виде
= Е d, получим
ε o εS
C
d
d – расстояние между обкладками
конденсатора, если между
обкладками вакуум, то ε = 1.
73
42
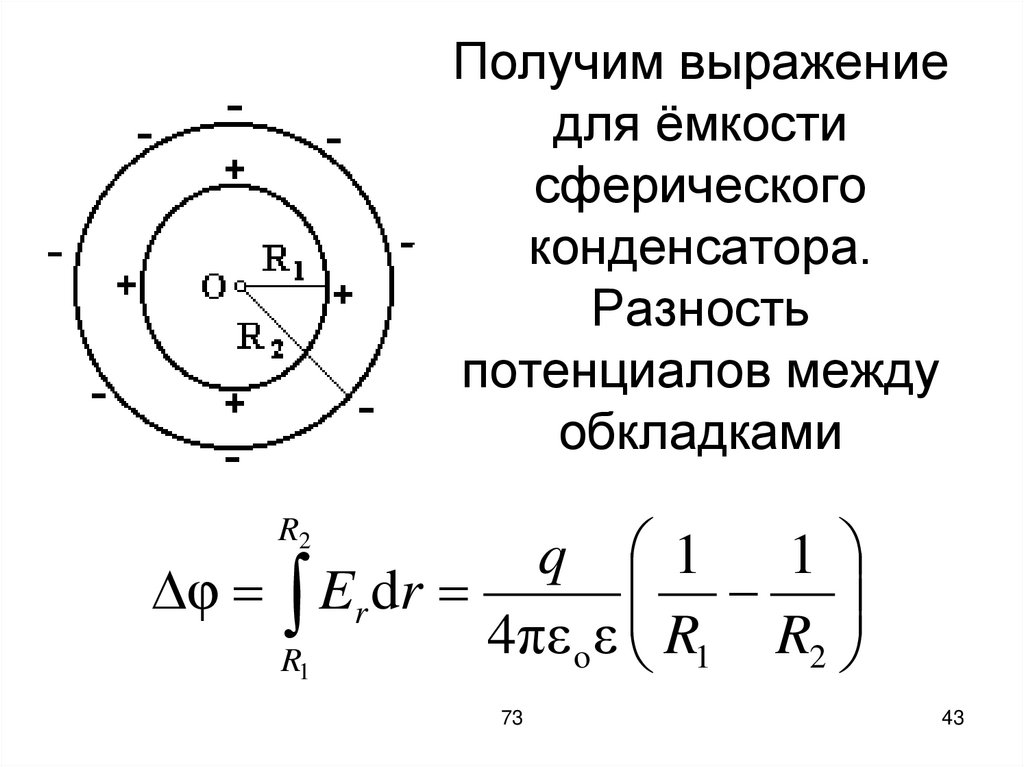
43. Получим выражение для ёмкости сферического конденсатора. Разность потенциалов между обкладками
q 11
φ Er dr
4πε o ε R1 R2
R1
R2
73
43
44. Следовательно, емкость сферического конденсатора, с учетом того, что пространство между обкладками заполнено диэлектрической
средой спроницаемостью :
R1R2
C 4πε0ε
R2 R1
73
44
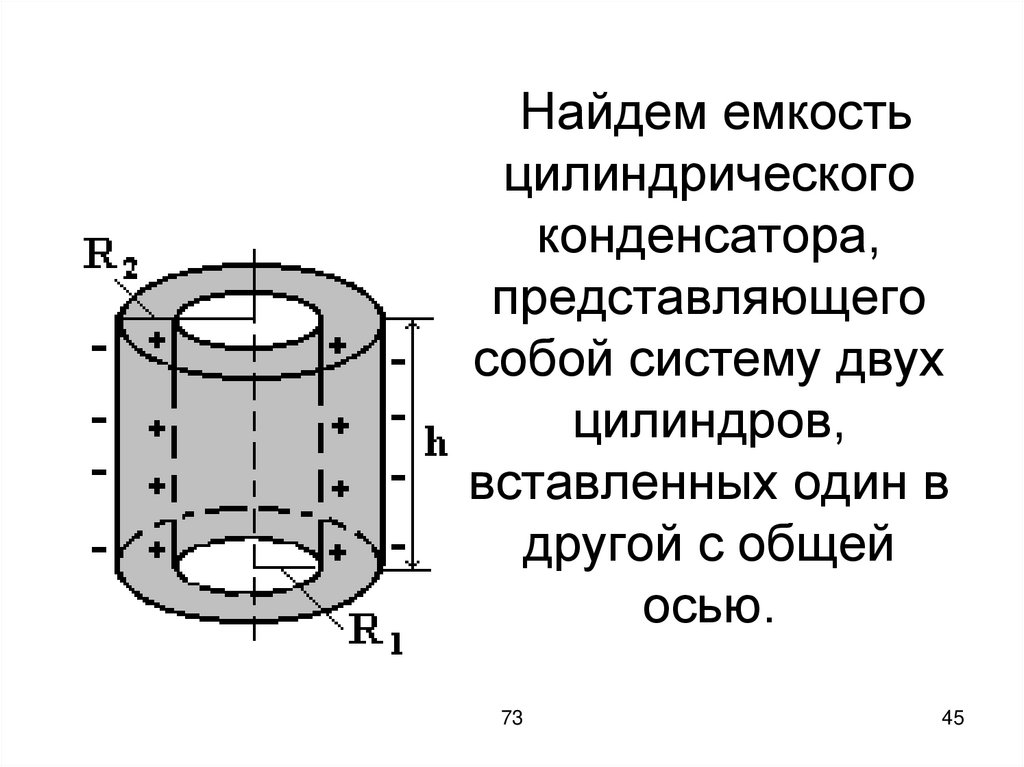
45. Найдем емкость цилиндрического конденсатора, представляющего собой систему двух цилиндров, вставленных один в другой с общей
осью.73
45
46. Проводя аналогичные рассуждения, как и в случае со сферическим конденсатором, получим
2πε0εhC
R2
ln
R1
73
46
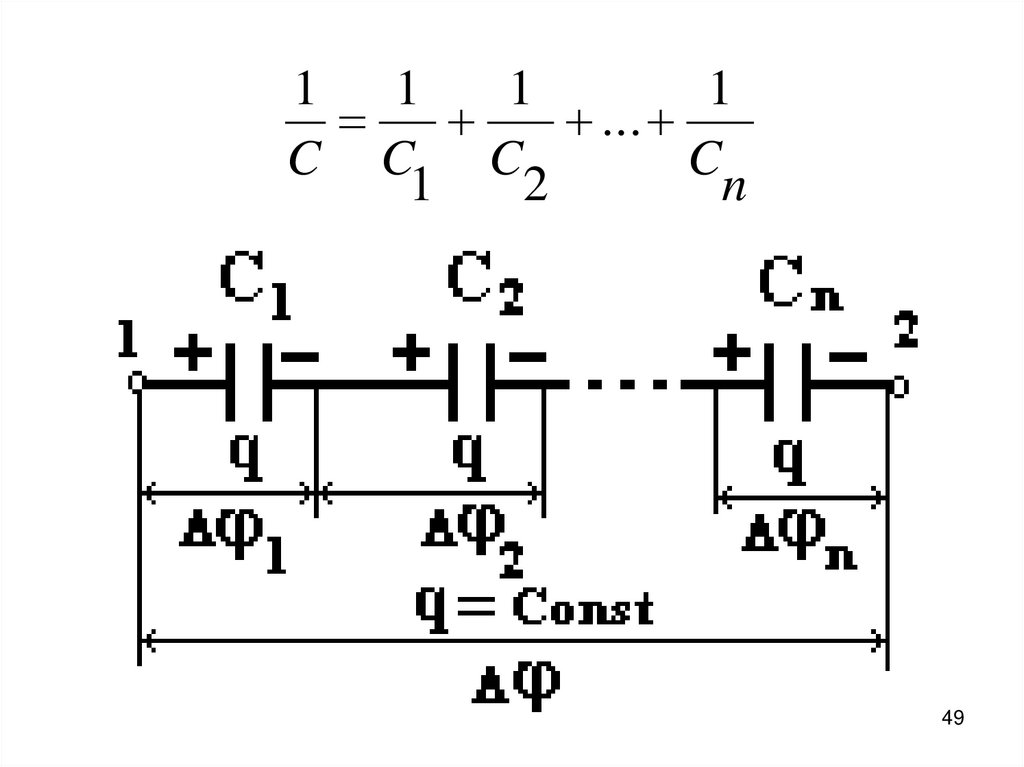
47. Последовательное соединение конденсаторов. Все внутренние обкладки при последовательном соединении электризуются через влияние.
Их заряды равны по величине, нопротивоположны по знаку
( + q = – q = q).
73
47
48. Следовательно, заряды на всех конденсаторах при последовательном их соединении равны, а потенциалы складываются = 1 – 2 =
Следовательно, заряды на всехконденсаторах при
последовательном их соединении
равны, а потенциалы складываются
= 1 – 2 = 1 + 2 + ... + n
73
48
49.
11
1
1
...
C C C
C
1
2
n
73
49
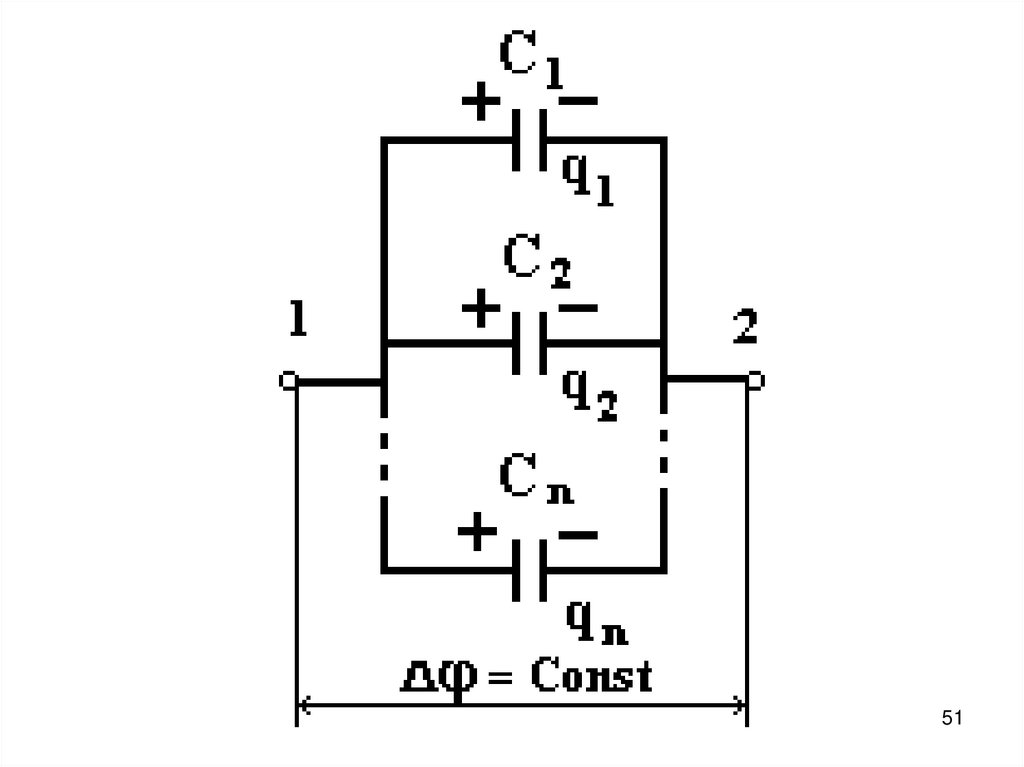
50. При параллельном соединении все конденсаторы имеют постоянную разность потенциалов 1 – 2 = const. Полный заряд батареи
При параллельном соединении всеконденсаторы имеют постоянную
разность потенциалов
1 – 2 = const.
Полный заряд батареи
конденсаторов складывается
q = q1 + q2 +...+ qn.
Ёмкость батареи конденсаторов
С = С1 + С2 + ... + Сn.
73
50
51.
7351
52.
7352
53. 11. Ёмкостные коэффициенты. Энергия заряженного конденсатора. Объёмная плотность электрической энергии. Сила взаимодействия
обкладокконденсатора.
73
53
54. Решения задачи о нахождении электрических полей в системе N статических заряженных проводников упрощаются, если воспользоваться
следующимсвойством: заряды проводников
являются линейными, однородными
функциями их потенциалов, а
потенциалы линейными,
однородными функциями зарядов.
73
54
55. Коэффициенты этих линейных зависимостей называют емкостными коэффициентами, которые определяются размерами, формой и взаимным
расположениемпроводников.
73
55
56. Если пространство между проводниками заполнено однородным диэлектриком, в котором нет свободных зарядов, то емкостные
коэффициенты прямопропорциональны его
диэлектрической проницаемости.
73
56
57. Согласно линейности и однородности уравнений электростатики (например, уравнение Лапласа) аналитически это свойство
записывается в видеN
qi Cij φ j
j 1
73
57
58. где qi заряд i-го проводника; j потенциал j-го проводника; Сij емкостные коэффициенты (индексы i, j = 1, 2, ... , N).
где qi заряд i-го проводника;j потенциал j-го проводника;
Сij емкостные коэффициенты
(индексы i, j = 1, 2, ... , N).
73
58
59. В свою очередь, емкостные коэффициенты характеризуются следующими свойствами: 1) Сij = Сji; 2) Сii 0 для всех i.
В свою очередь, емкостныекоэффициенты характеризуются
следующими свойствами: 1) Сij = Сji;
2) Сii 0 для всех i. Действительно,
емкостные коэффициенты Сij с
одинаковыми индексами (i = j)
положительны. Заземлим все
проводники, кроме i-го,
тогда qi = Cii i. Но величины qi и i
имеют одинаковые знаки.
Следовательно, Сii 0.
73
59
60. 3) Сij 0, если i j, т. е. емкостные коэффициенты с различными индексами отрицательны. Действительно, заземлим все
3) Сij 0, если i j, т. е. емкостныекоэффициенты с различными
индексами отрицательны.
Действительно, заземлим все
проводники, кроме i-го и j-го.
Сообщим i-му проводнику
положительный заряд (qi 0), а j-й
останется не заряженным (qj = 0),а
потенциалы i и j будут
положительными.
73
60
61. Причем qj = Сjii + Cjjj = 0, что возможно, если Сji 0. Во всех случаях потенциал поля в бесконечности равен нулю. Если
Причем qj = Сji i + Cjj j = 0, чтовозможно, если Сji 0. Во всех
случаях потенциал поля в
бесконечности равен нулю.
Если число проводников (обкладок
конденсатора) равно двум, то
q1 = C11 1 + C12 2,
q2 = C21 1 + C22 2,
+q = q = q.
73
61
62. Решая эти уравнения относительно 1 и 2, находим разность потенциалов и емкость конденсатора
Решая эти уравнения относительно1 и 2, находим разность
потенциалов и емкость конденсатора
C11C22 C12C21
C
C11 C12 C21 C22
73
62
63.
7363
64. Потенциальная энергия заряда q0 в поле системы зарядов и потенциальная энергия системы зарядов, соответственно:
qi q j1
Wp
2 i j 4 πε0 rij
qi q0
Wp
i 1 4 πε0 ri
n
73
64
65. Первое выражение можно представить в виде (энергия одного заряда в системе зарядов) Wpi = qi i, где qi – i-й заряд системы; i
Первое выражение можнопредставить в виде (энергия одного
заряда в системе зарядов) Wpi = qi i,
где qi – i-й заряд системы; i –
результирующий потенциал,
создаваемый всеми остальными
зарядами системы в месте
нахождения заряда qi.
73
65
66. Просуммировав энергию каждого заряда можно получить энергию всей системы
1 NW qi φ i
2 i 1
73
66
67. Если заряды распределены по объему с объемной плотностью заряда , то систему зарядов можно представить как совокупность
Если заряды распределены пообъему с объемной плотностью
заряда , то систему зарядов можно
представить как совокупность
элементарных зарядов
dq = dV, т. е. dW = dq = dV.
С учетом этого предыдущая
формула принимает вид
1
W φρdV
2V
73
67
68. Используя эту формулу найдем энергию изолированного (уединенного) проводника. Если проводник имеет заряд q и потенциал =
Используя эту формулу найдемэнергию изолированного
(уединенного) проводника.
Если проводник имеет заряд q и
потенциал = const во всех точках,
где распределен заряд, то
1
qφ q
Cφ
W φ ρdV
2 V
2 2C
2
2
73
2
68
69. Так как для плоского конденсатора (два заряженных проводника) q = C , то Для нахождения энергии мы использовали только заряды
Так как для плоского конденсатора(два заряженных проводника)
q = C , то
q φ q
C φ
W
2
2C
2
2
2
Для нахождения энергии мы
использовали только заряды и
потенциалы.
73
69
70. Основной характеристикой электрического поля является вектор напряженности Е. Тогда энергию электрического поля между
обкладками плоского конденсатораможно найти, преобразуя
предыдущую формулу с учетом того,
что = Е d, C = ε0 ε S / d и V = S d:
ε oεE
W
V
2
2
73
70
71. Если поделить энергию заряженного конденсатора W на его объём V, то получим объёмную плотность энергии для электростатического
поля (выражение получено изусловий для однородного поля, но
оно справедливо и для
неоднородных полей)
ε 0ε E
w
2
73
2
71
72. Возьмём выражение для энергии заряженного плоского конденсатора и продифференцируем его по направлению перпендикулярному
плоскости обкладок2
2
q
q
W
d
2C 2ε 0εS
73
72
73. Мы получили силу, с которой обкладки конденсатора притягивают друг друга.
F grad W2
2
d
d
q
d
q
Fx W
d
x
dx
dx 2ε 0εS
dx 2ε 0εS
2
q
F
2ε 0εS
Мы получили силу, с которой
обкладки конденсатора притягивают
друг друга.
73
73
















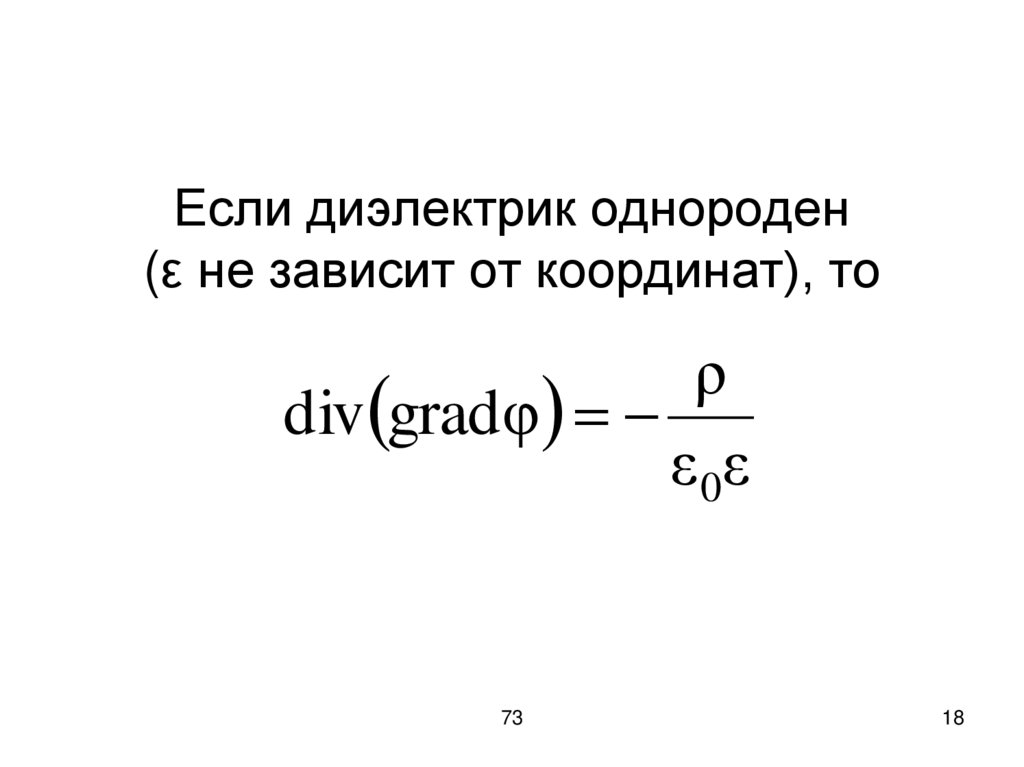

















































 Физика
Физика