Похожие презентации:
Треугольники общего вида
1.
Работу выполнили Афонина А., Вельш Л., Гуляева В.,Коновалова А., Кристюк А.
2.
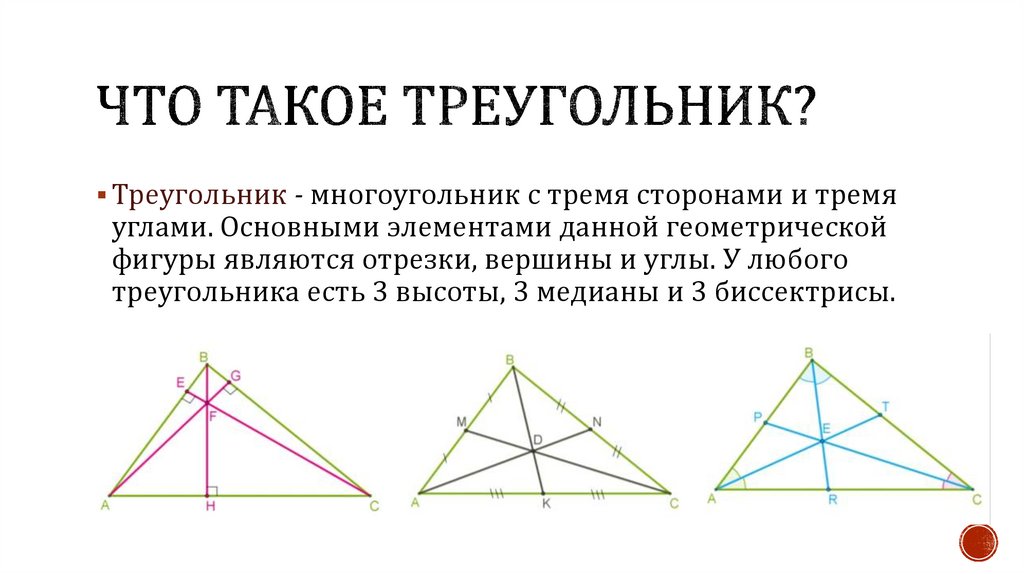
Треугольник - многоугольник с тремя сторонами и тремяуглами. Основными элементами данной геометрической
фигуры являются отрезки, вершины и углы. У любого
треугольника есть 3 высоты, 3 медианы и 3 биссектрисы.
3.
СУММА УГЛОВИ ВНЕШНИЕ УГЛЫ
4.
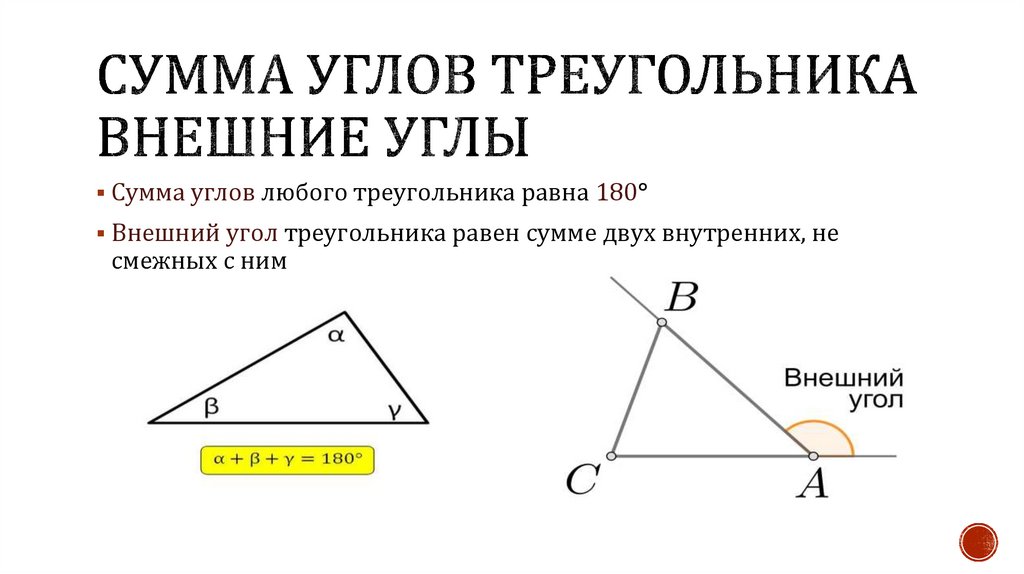
Сумма углов любого треугольника равна 180°Внешний угол треугольника равен сумме двух внутренних, не
смежных с ним
5.
ВИДЫТРЕУГОЛЬНИКОВ
6.
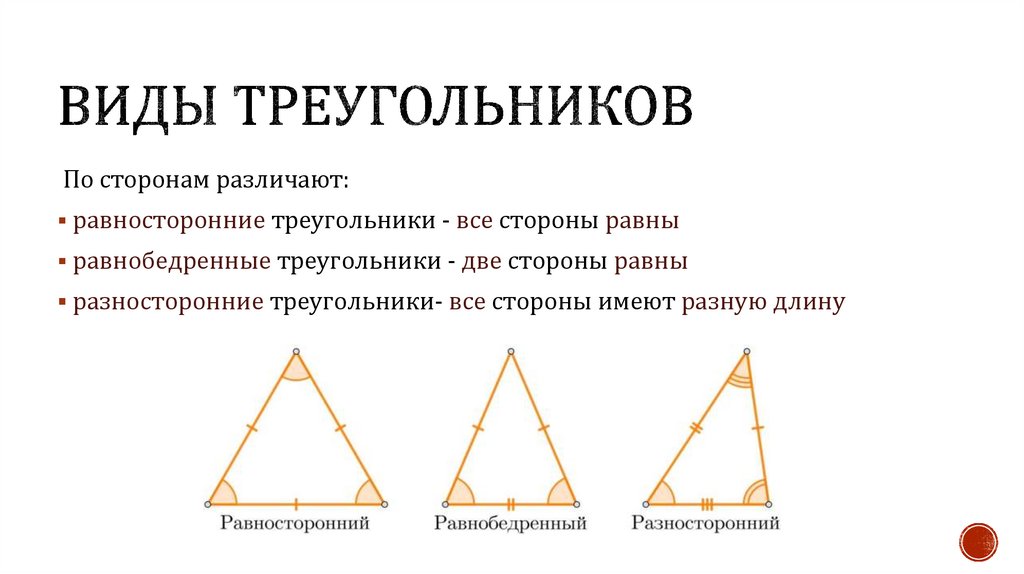
По сторонам различают:равносторонние треугольники - все стороны равны
равнобедренные треугольники - две стороны равны
разносторонние треугольники- все стороны имеют разную длину
7.
РАВНОСТОРОННИЙ △8.
ТРЕУГОЛЬНИКАЕсли у треугольника все три угла равны,
то этот треугольник - равносторонний
Если медианы, высоты и биссектрисы
пересекаются в центре треугольника, то
этот треугольник - равносторонний
9.
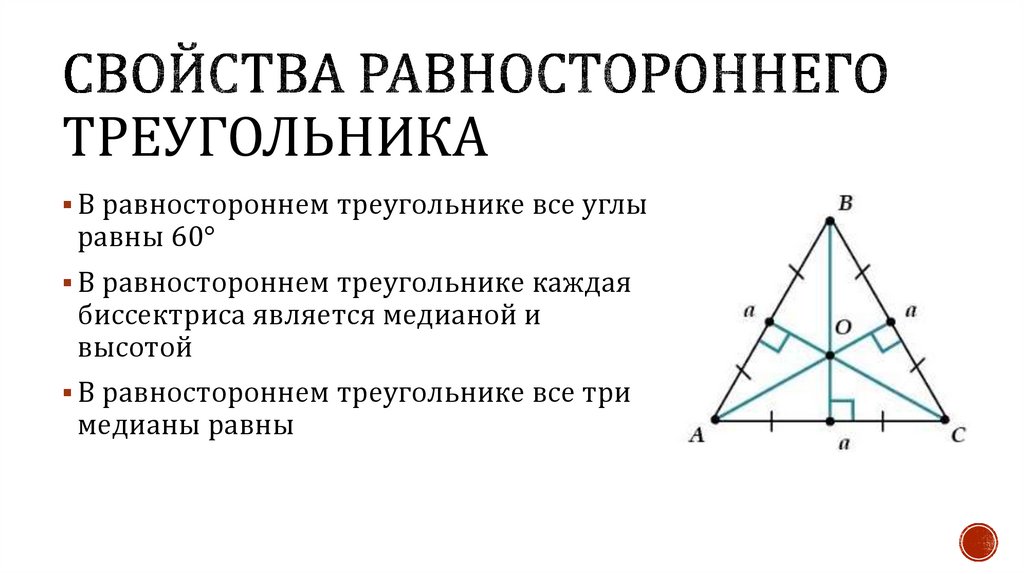
ТРЕУГОЛЬНИКАВ равностороннем треугольнике все углы
равны 60°
В равностороннем треугольнике каждая
биссектриса является медианой и
высотой
В равностороннем треугольнике все три
медианы равны
10.
РАВНОБЕДРЕННЫЙ △11.
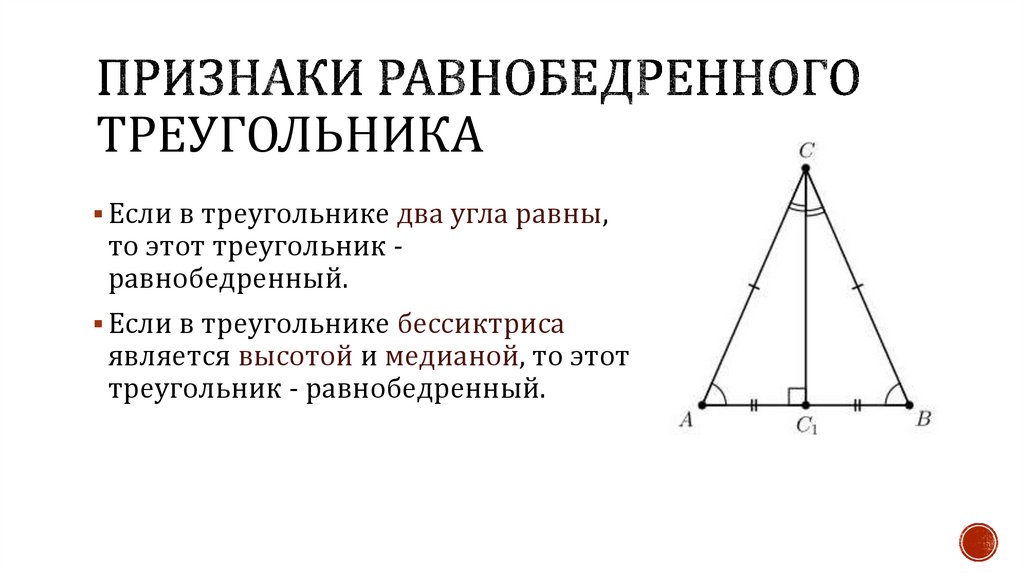
ТРЕУГОЛЬНИКАЕсли в треугольнике два угла равны,
то этот треугольник равнобедренный.
Если в треугольнике бессиктриса
является высотой и медианой, то этот
треугольник - равнобедренный.
12.
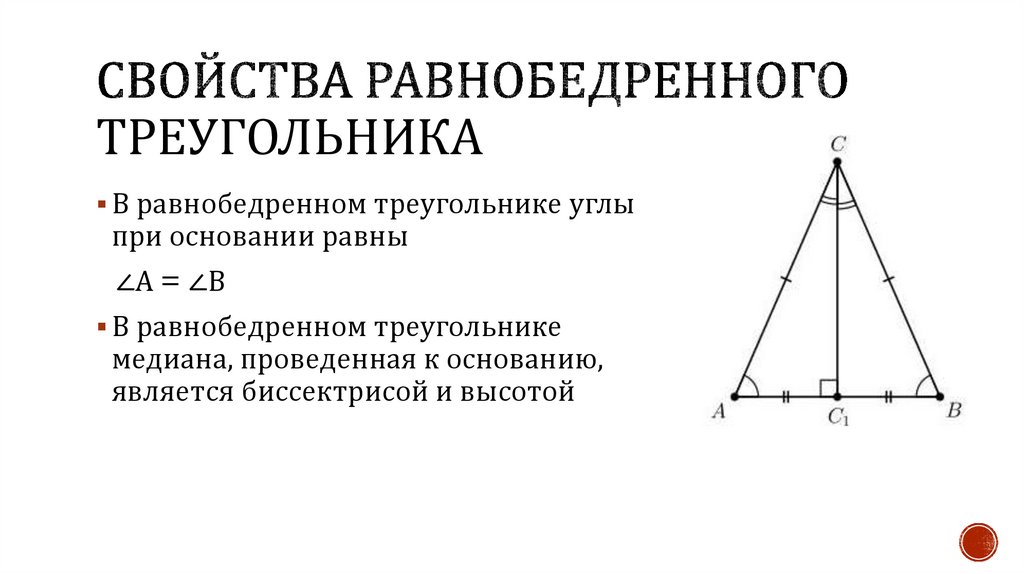
ТРЕУГОЛЬНИКАВ равнобедренном треугольнике углы
при основании равны
∠A = ∠B
В равнобедренном треугольнике
медиана, проведенная к основанию,
является биссектрисой и высотой
13.
ПРИЗНАКИ РАВЕНСТВА14.
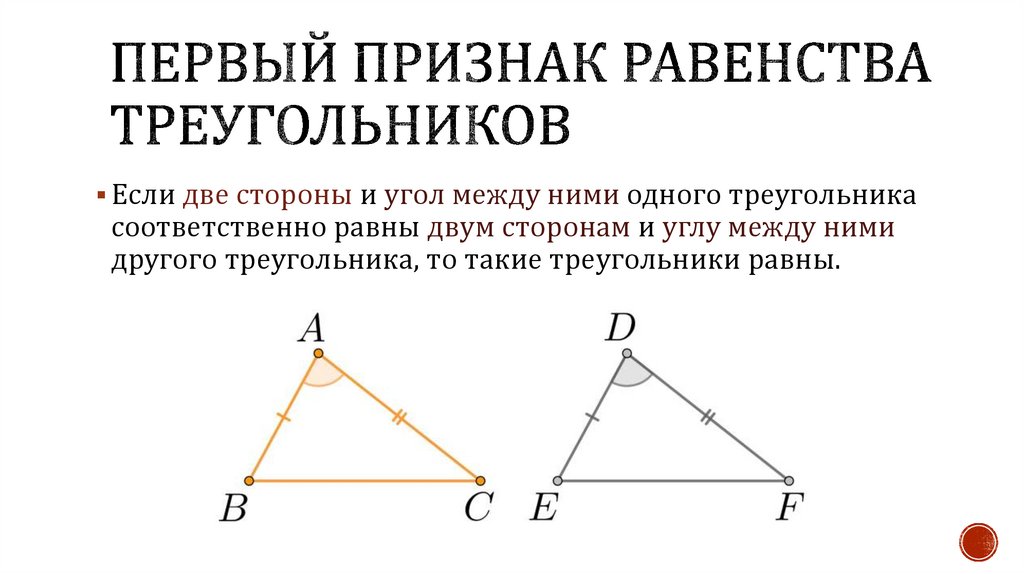
Если две стороны и угол между ними одного треугольникасоответственно равны двум сторонам и углу между ними
другого треугольника, то такие треугольники равны.
15.
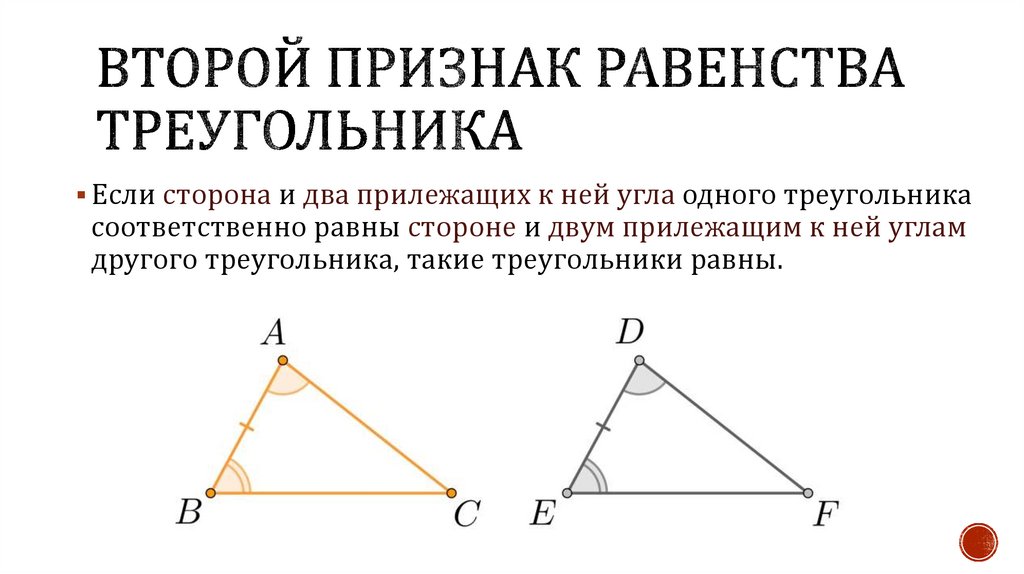
Если сторона и два прилежащих к ней угла одного треугольникасоответственно равны стороне и двум прилежащим к ней углам
другого треугольника, такие треугольники равны.
16.
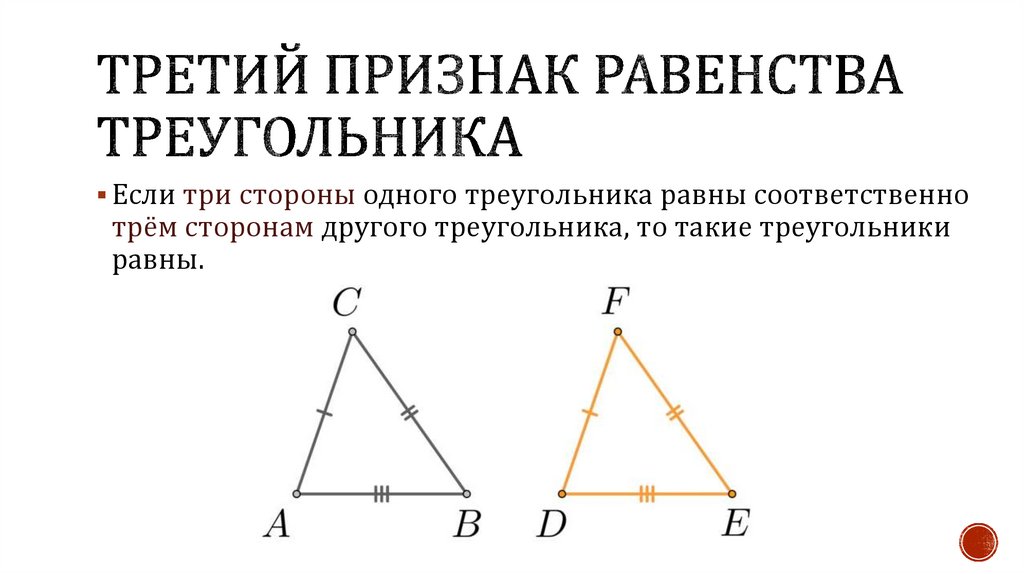
Если три стороны одного треугольника равны соответственнотрём сторонам другого треугольника, то такие треугольники
равны.
17.
ПРИЗНАКИ ПОДОБИЯ18.
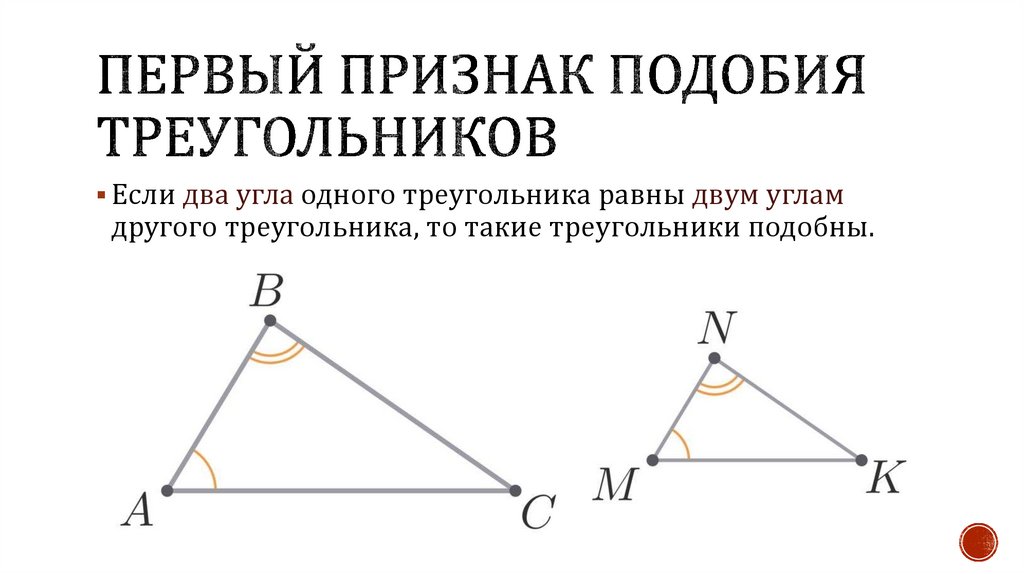
Если два угла одного треугольника равны двум угламдругого треугольника, то такие треугольники подобны.
19.
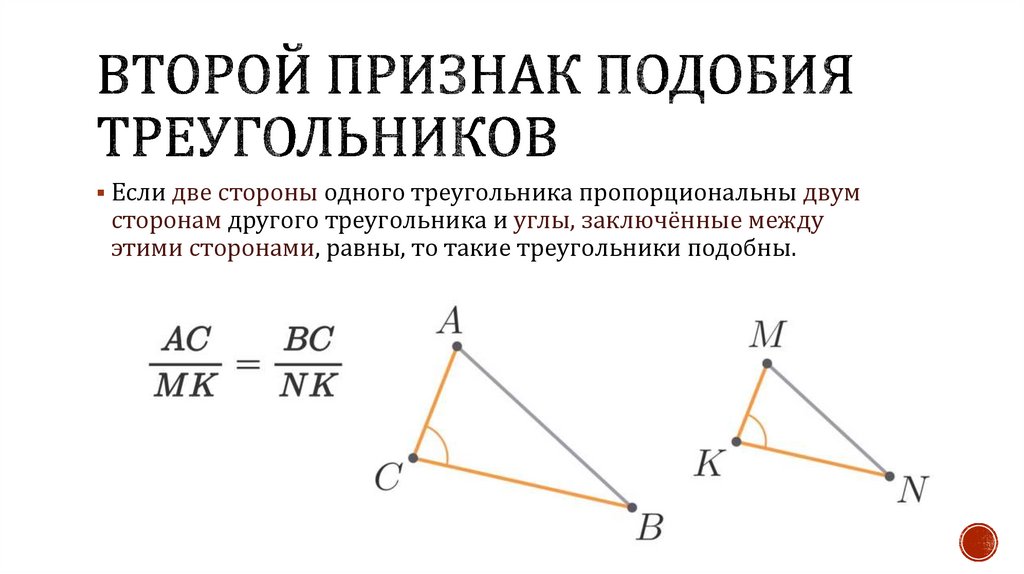
Если две стороны одного треугольника пропорциональны двумсторонам другого треугольника и углы, заключённые между
этими сторонами, равны, то такие треугольники подобны.
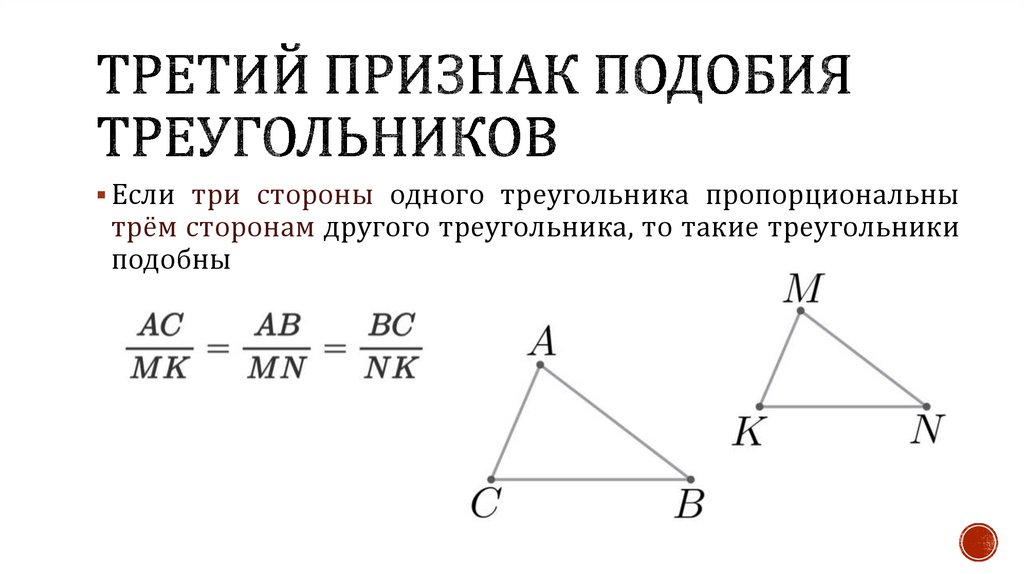
20.
Если три стороны одного треугольника пропорциональнытрём сторонам другого треугольника, то такие треугольники
подобны
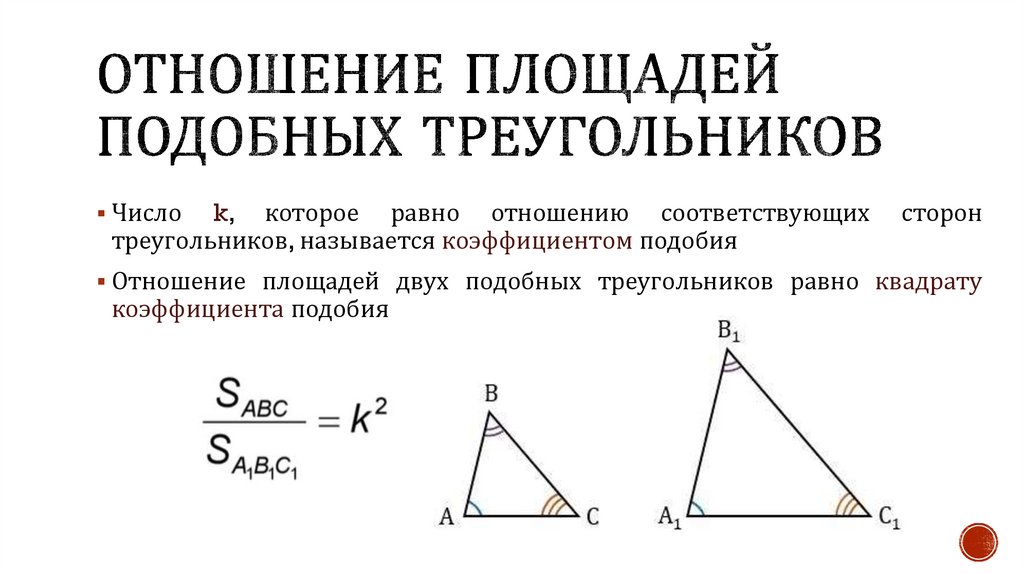
21.
Числоk, которое равно отношению соответствующих
треугольников, называется коэффициентом подобия
сторон
Отношение площадей двух подобных треугольников равно квадрату
коэффициента подобия
22.
СРЕДНЯЯ ЛИНИЯ △23.
Средняя линия – отрезок, соединяющий середины двух его сторонСредняя линия равна половине стороны, которой параллельна
24.
ПЛОЩАДЬ △25.
Площадь треугольника равнаполовине произведения его
основания на высоту
26.
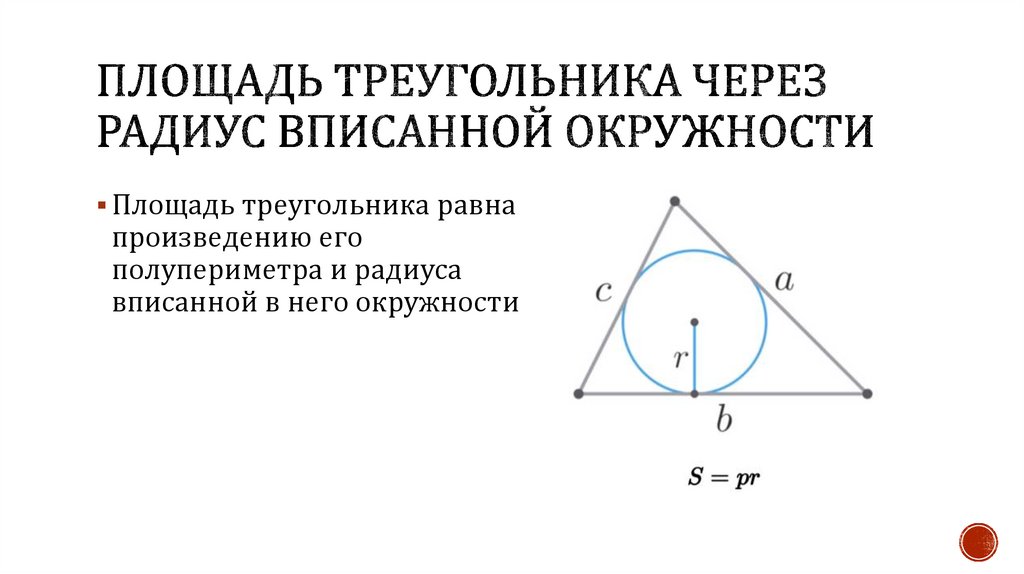
Площадь треугольника равнапроизведению его
полупериметра и радиуса
вписанной в него окружности
27.
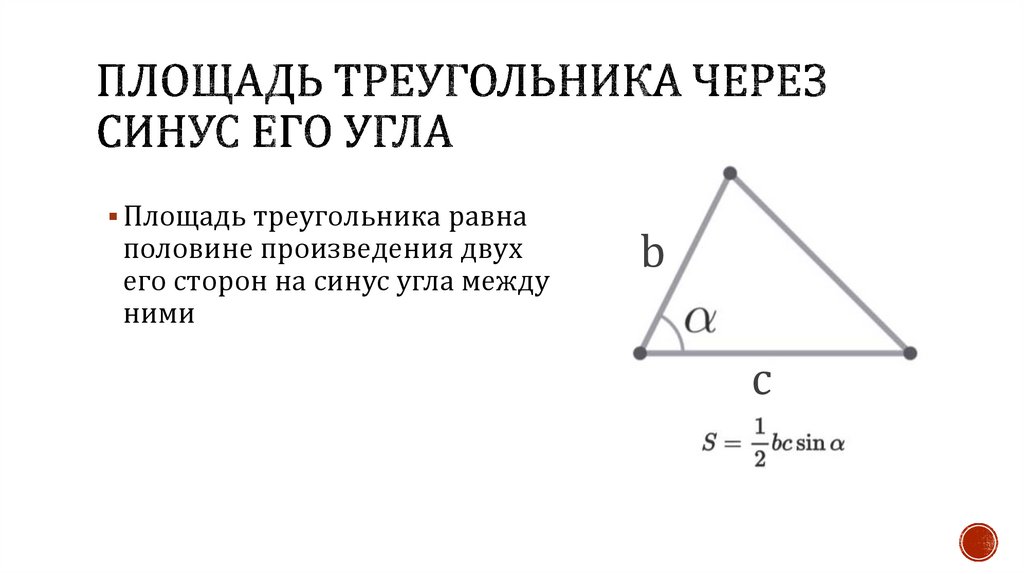
Площадь треугольника равнаполовине произведения двух
его сторон на синус угла между
ними
b
c
28.
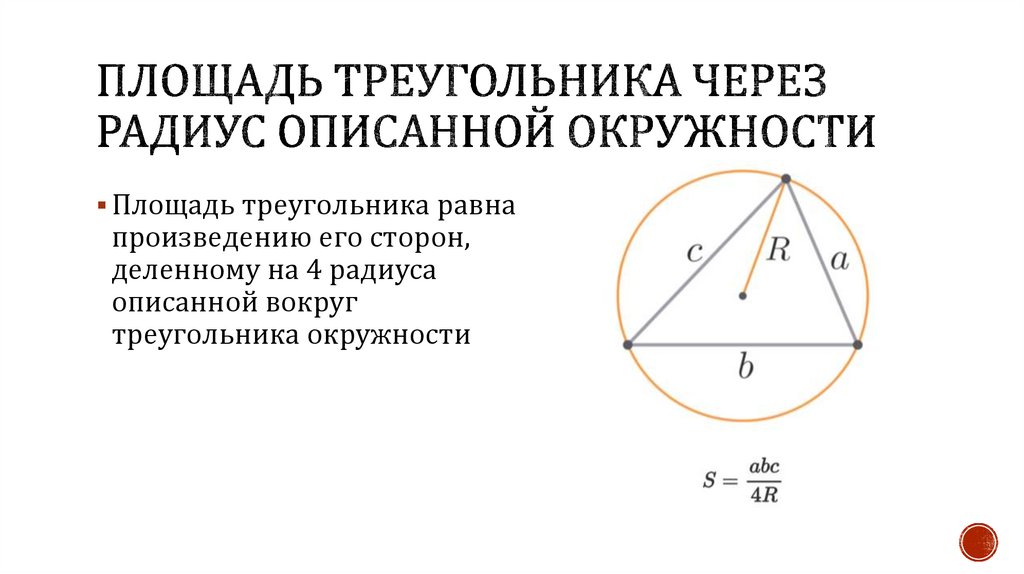
Площадь треугольника равнапроизведению его сторон,
деленному на 4 радиуса
описанной вокруг
треугольника окружности
29.
a, b, c - стороныp - полупериметр
30.
ТЕОРЕМА СИНУСОВ ИКОСИНУСОВ
31.
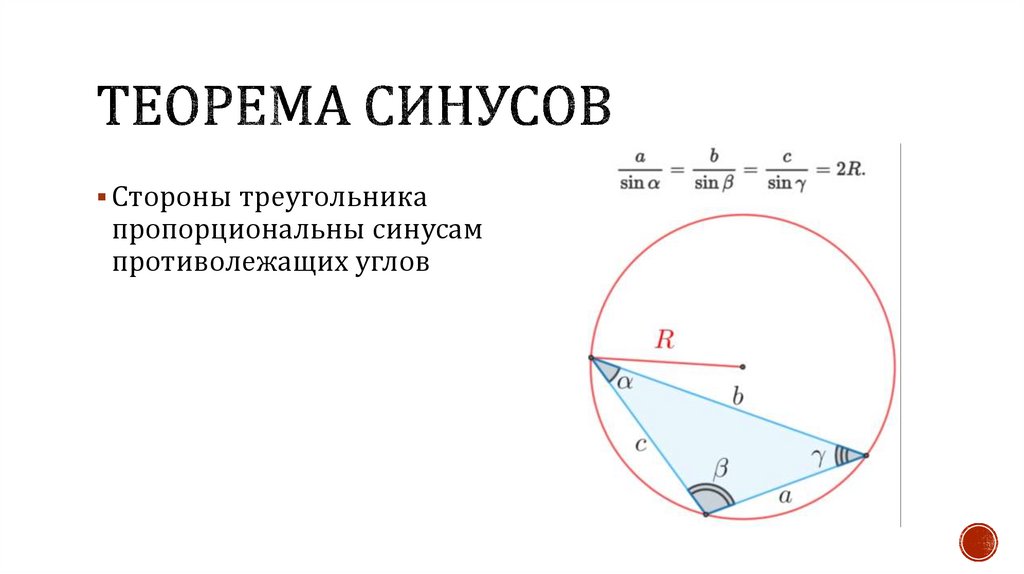
Стороны треугольникапропорциональны синусам
противолежащих углов
32.
Квадрат стороны треугольникаравен сумме квадратов двух
других его сторон минус
удвоенное произведение этих
сторон на косинус угла между
ними
33.
ВПИСАННЫЙ ИОПИСАННЫЙ △
34.
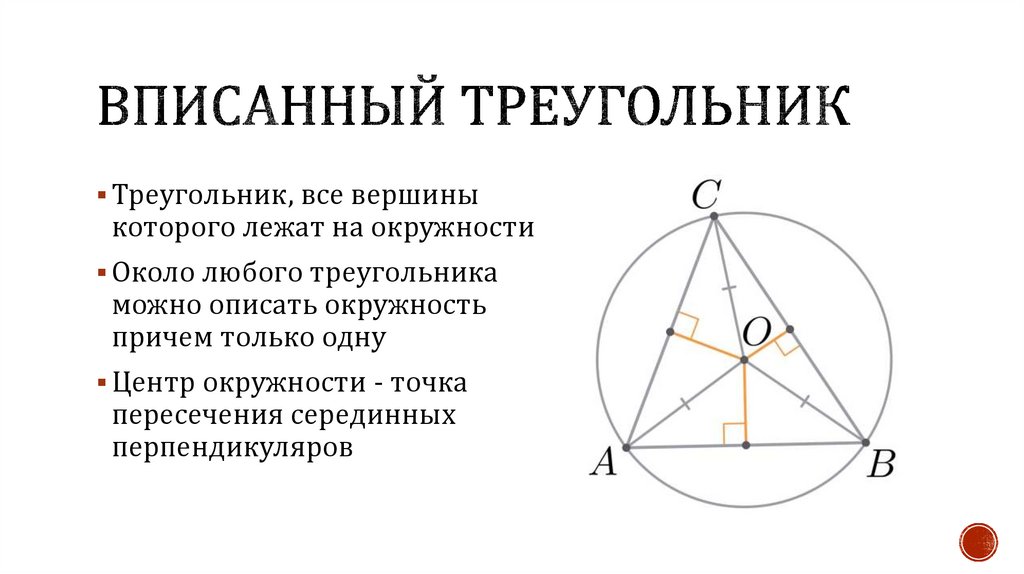
Треугольник, все вершиныкоторого лежат на окружности
Около любого треугольника
можно описать окружность
причем только одну
Центр окружности - точка
пересечения серединных
перпендикуляров
35.
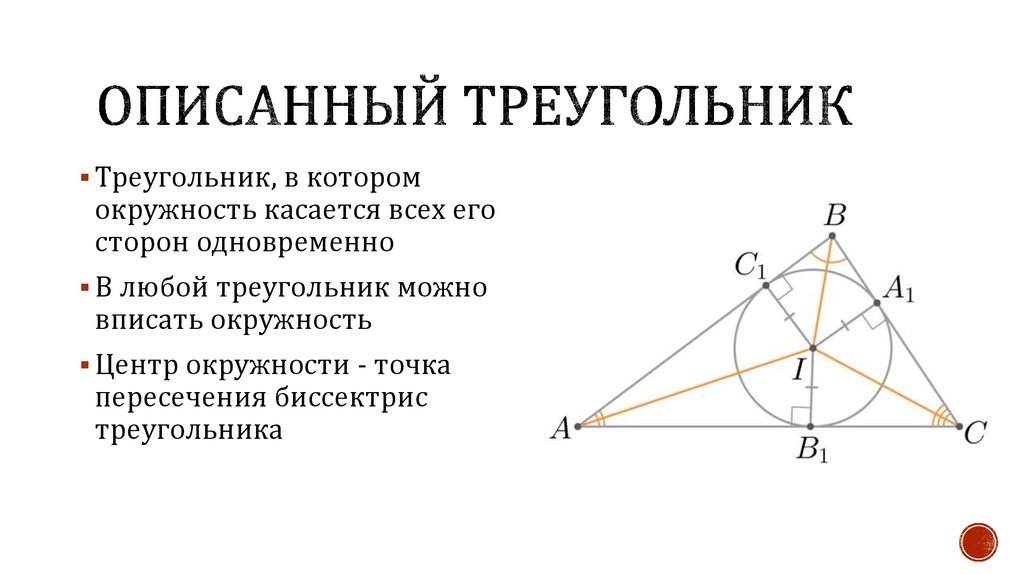
Треугольник, в которомокружность касается всех его
сторон одновременно
В любой треугольник можно
вписать окружность
Центр окружности - точка
пересечения биссектрис
треугольника










 Математика
Математика