Похожие презентации:
Метрические задачи. (Лекция 3)
1.
Лекция 3. Метрические задачи.К метрическим задачам относятся :
•Задачи на определение действительного вида отрезка
прямой или плоской фигуры;
•Задачи на определение углов наклона отрезка прямой
линии и плоской фигуры;
•Задачи на определение расстояний между объектами
проецирования ( точкой и прямой, двумя прямыми,
прямой и плоскостью, двумя плоскостями)
1
2.
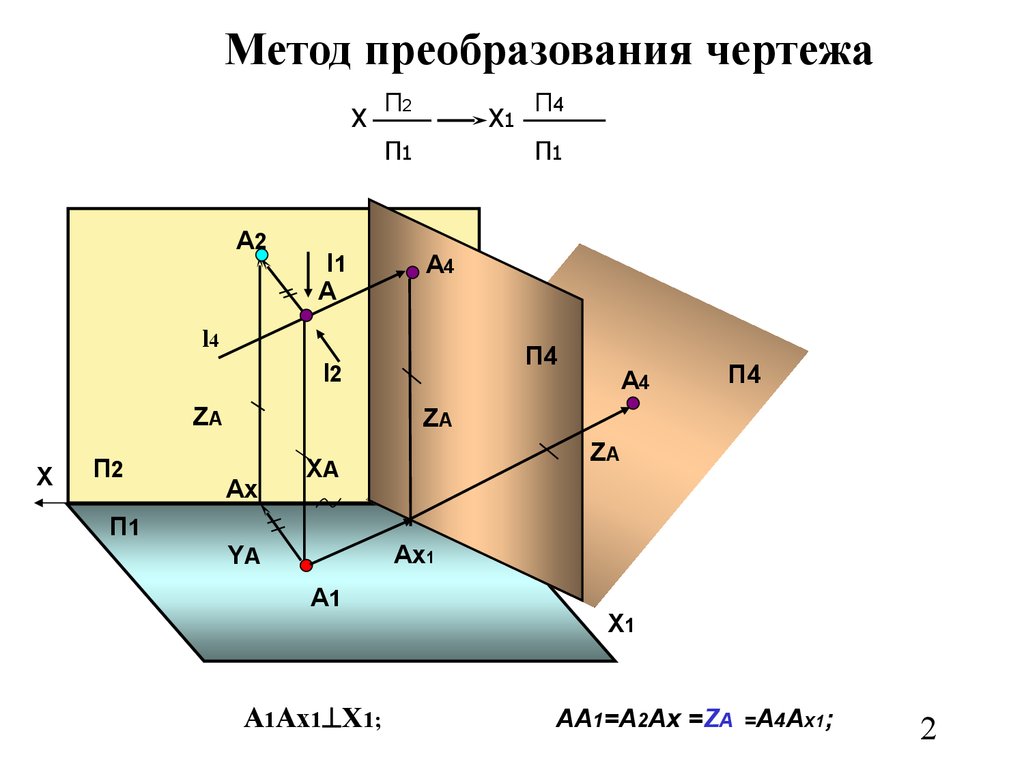
Метод преобразования чертежаХ
П2
Х1
П1
А2
l1
А
П1
А4
l4
П4
l2
ZА
Х
П2
П4
А4
П4
ZА
Ах
ZА
ХА
П1
0
Ах1
YА
А1
А1Ах1 Х1;
Х1
АА1=А2Ах =ZА =А4Ах1;
2
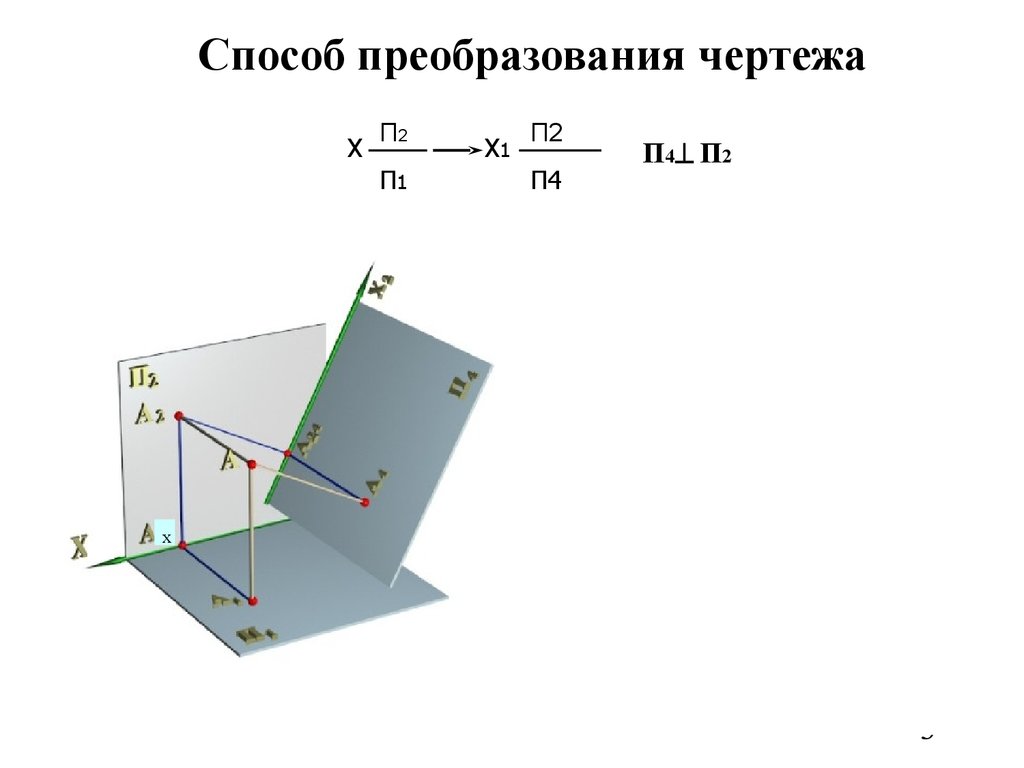
3. Способ преобразования чертежа
ХП2
П1
Х1
П2
П4
П4 П2
х2
х
х
3
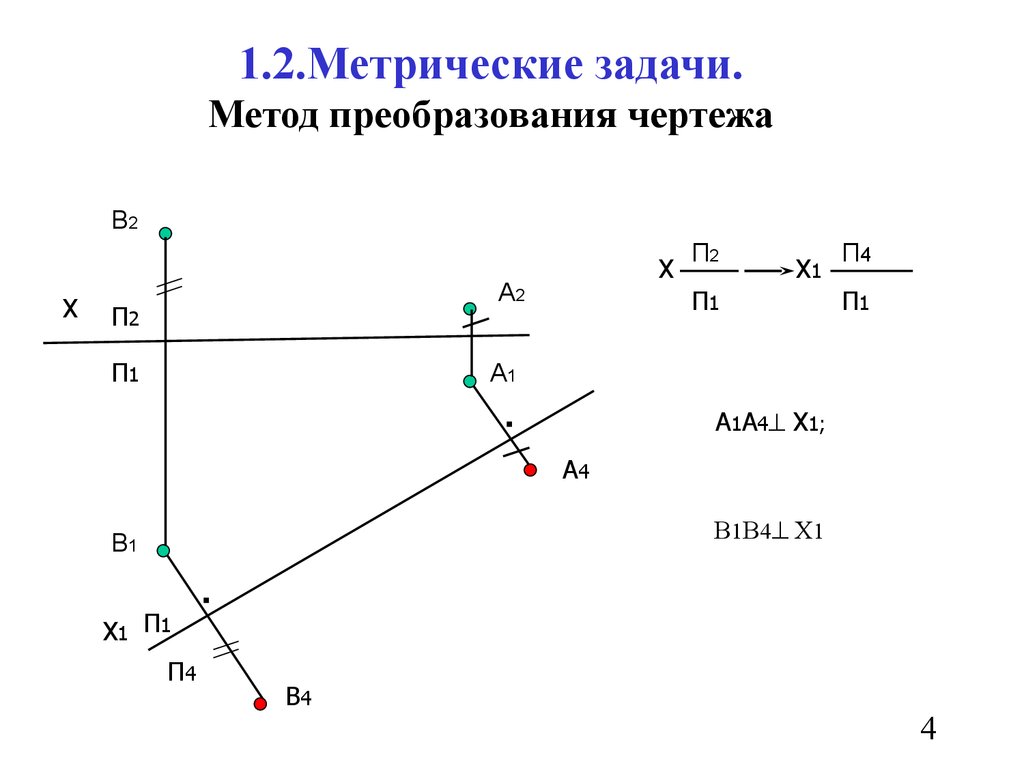
4. 1.2.Метрические задачи. Метод преобразования чертежа
В2Х
Х
А2
П2
П1
П2
Х1
П1
П4
П1
А1
А1А4 Х1;
▪
А4
В1В4 Х1
В1
Х1 П1
П4
▪
В4
4
5. 1.2.Метрические задачи. Метод преобразования чертежа
В2Х
Х
А2
П2
П1
П2
Х1
П1
П4
П1
Х1//А1В1
А1
А1А4 Х1; В1В4 Х1
А4
В1
Н.в.
Х1 П1
П4
В4
5
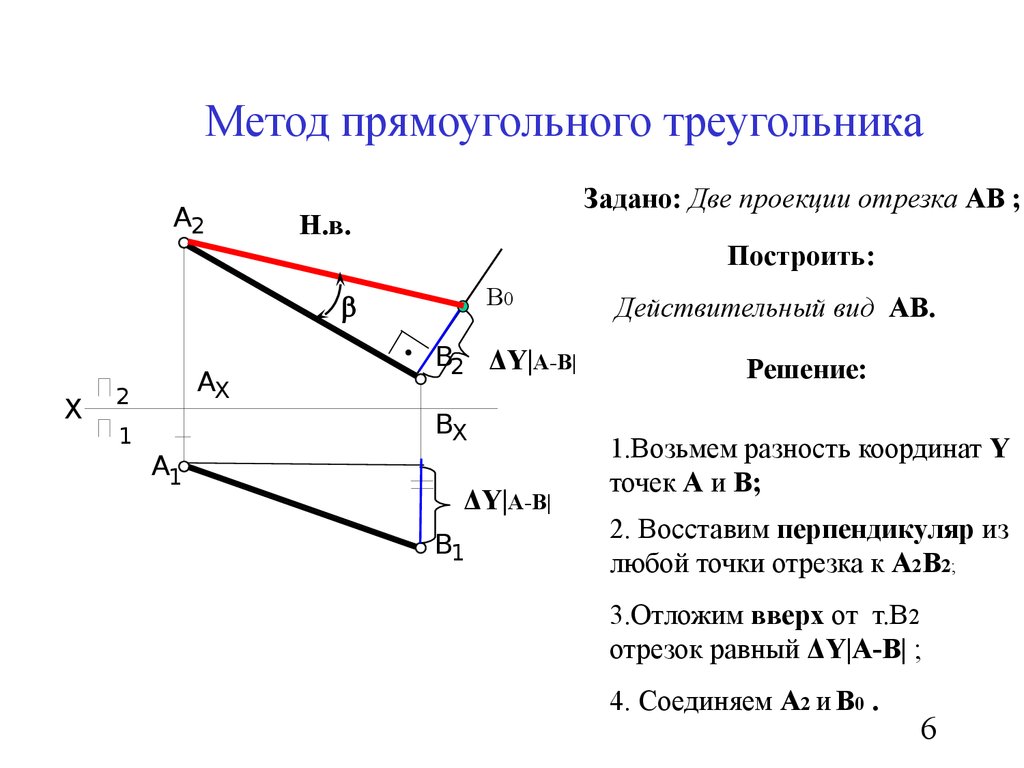
6. Метод прямоугольного треугольника
A2Задано: Две проекции отрезка АВ ;
Н.в.
Построить:
В0
X
AX
2
B2 ΔY|А-В|
BX
1
A1
ΔY|А-В|
B1
Действительный вид АВ.
Решение:
1.Возьмем разность координат Y
точек А и В;
2. Восставим перпендикуляр из
любой точки отрезка к А2В2;
3.Отложим вверх от т.В2
отрезок равный ΔY|А-В| ;
4. Соединяем А2 и В0 .
6
7. Определение углов наклона отрезка прямой линии
ZА5
Х2
C2
A2
X
C5
х
D2
γ
D3
BX
D5
A1
Y
B1
AX 1
BX 1
A4
C3
В5
B2
AX
2
1
β
X3
B4
HB
1
4
X1
7
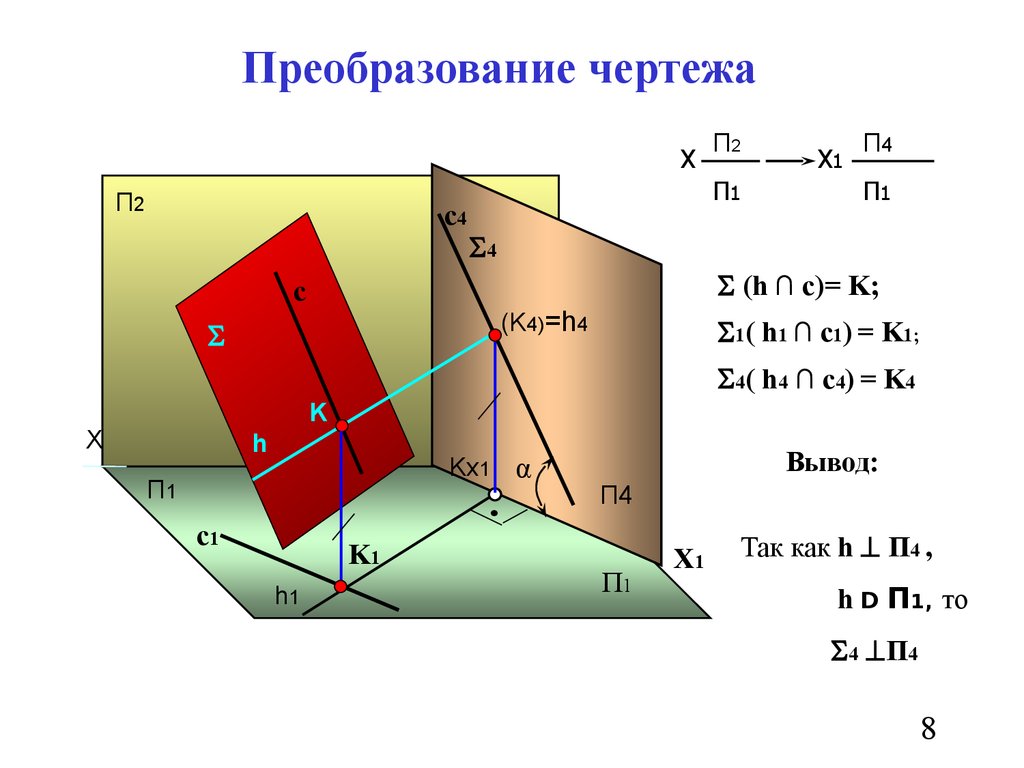
8. Преобразование чертежа
ХП2
c4
П2
Х1
П1
П4
П1
4
(h ∩ c)= K;
c
(K4)=h4
1( h1 ∩ c1) = K1;
4 ( h 4 ∩ c4 ) = K 4
K
Х
h
Kx1 α
П1
c1
K1
h1
Вывод:
П4
П1
X1
Так как h П4 ,
h D П1, то
4 П4
8
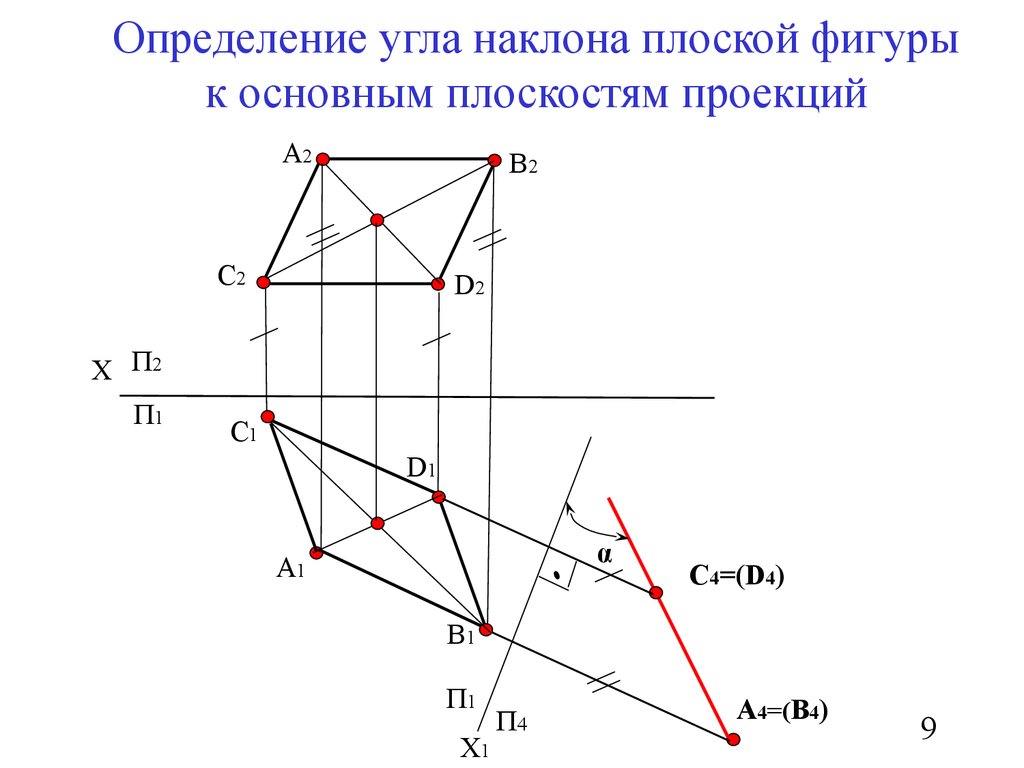
9. Определение угла наклона плоской фигуры к основным плоскостям проекций
А2В2
С2
D2
Х П2
П1
С1
D1
α
А1
С4=(D4)
В1
П1
Х1
П4
А4=(В4)
9
10. Определение действительного вида плоской фигуры
С4А4
В4
10
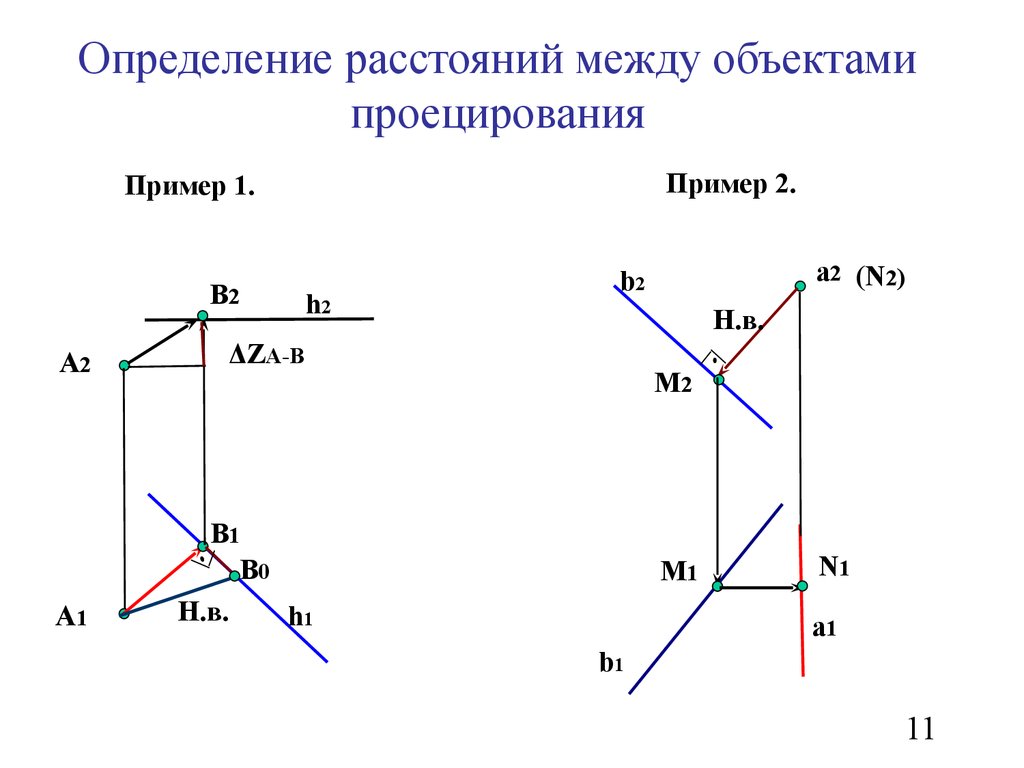
11. Определение расстояний между объектами проецирования
Пример 2.Пример 1.
В2
А2
А1
h2
а2 (N2)
b2
Н.в.
ΔZА-В
M2
В1
В0
Н.в.
h1
M1
N1
а1
b1
11
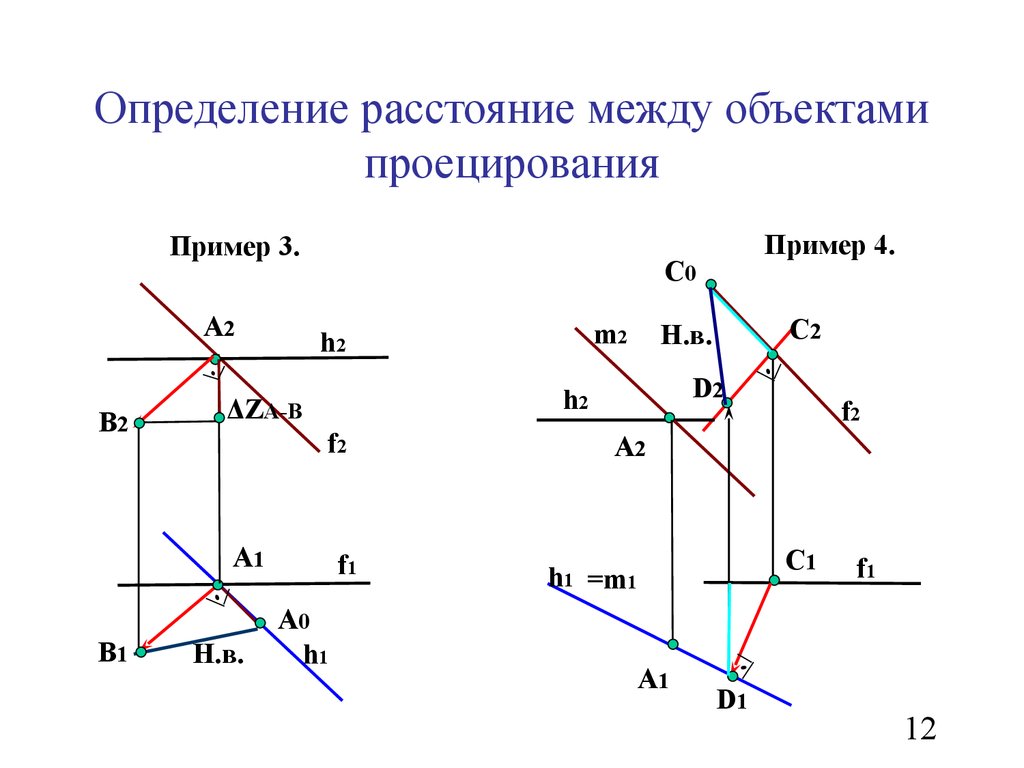
12. Определение расстояние между объектами проецирования
Пример 3.А2
В2
С0
f2
f1
А0
h1
С2
Н.в.
D2
h2
ΔZА-В
Н.в.
m2
h2
А1
В1
Пример 4.
f2
А2
С1
h1 =m1
А1
D1
f1
12
13.
Пример решения метрических задач13





 Математика
Математика Инженерная графика
Инженерная графика








