Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр

1. §5. Системы линейных уравнений

2. 6.1. Основные понятия

Системой
линейных
алгебраических
уравнений, содержащей m уравнений и n
неизвестных называется система вида
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
21 1
22 2
2n n
2
(1)
am 1 x1 am 2 x2 amn xn bm ,
где a ik – коэффициенты системы, bi
свободные члены (i 1, m, k 1, n ).
–

3.

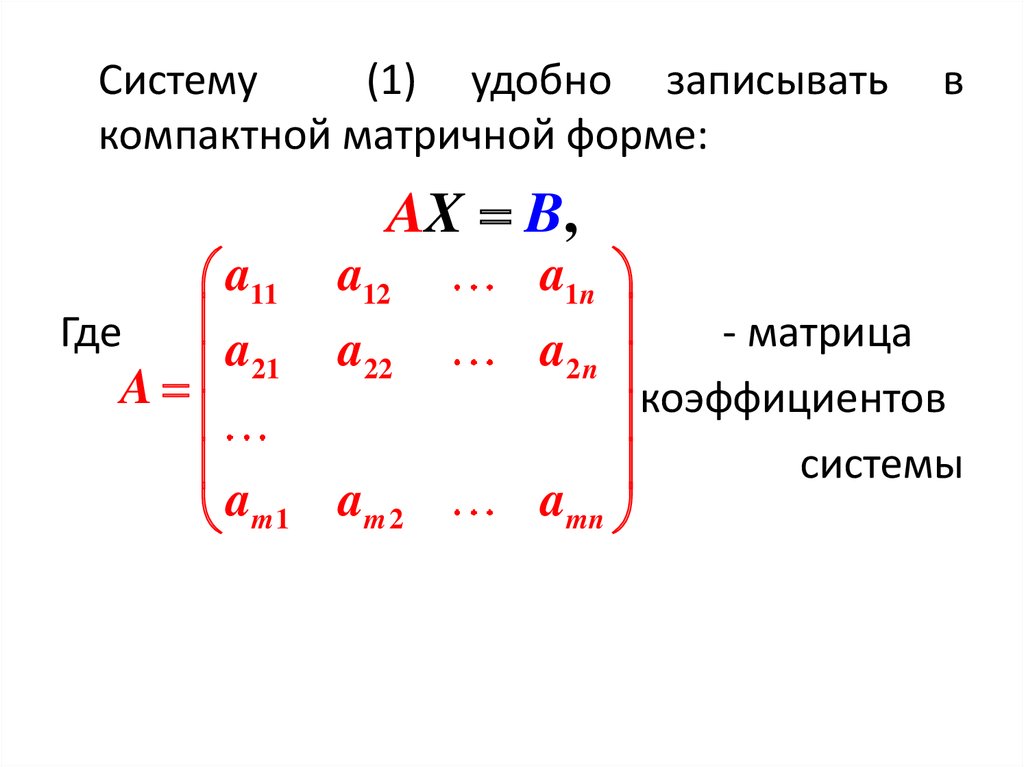
Систему
(1) удобно записывать
компактной матричной форме:
AX B,
a11 a12
Где
a
a
21
22
A
am 1 am 2
в
a1n
- матрица
a2 n
коэффициентов
системы
amn

4.

x1
x
2
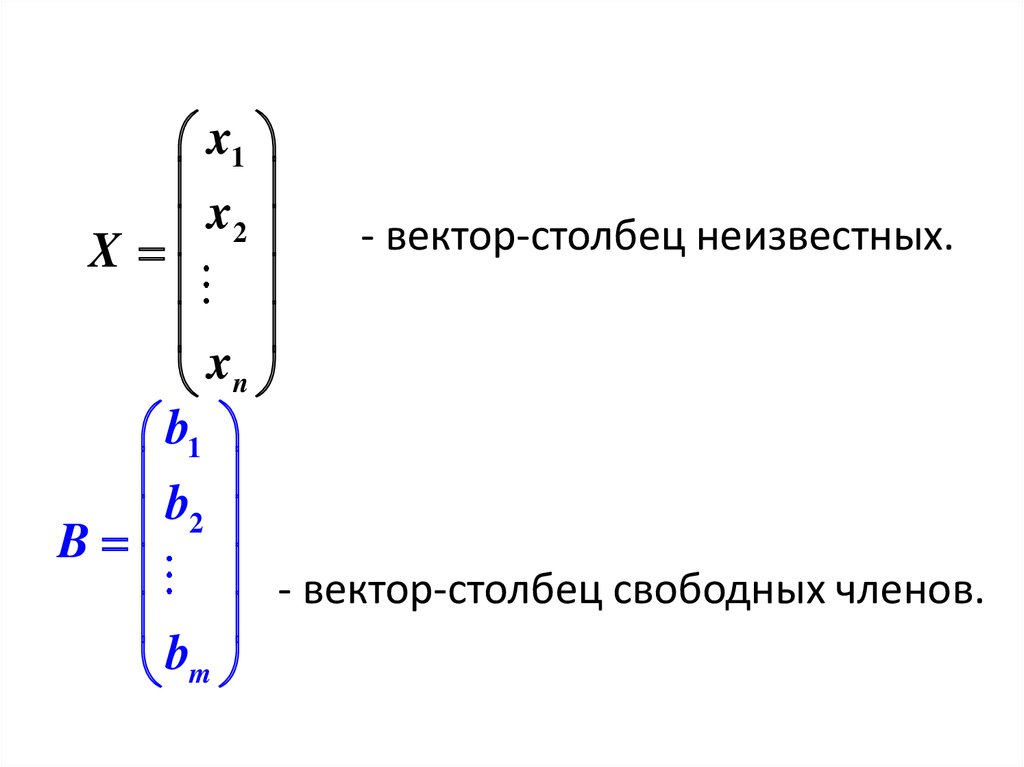
- вектор-столбец неизвестных.
X
xn
b1
b
2
B
- вектор-столбец свободных членов.
bm

5.

ОПР. Расширенной матрицей системы (1)
называется матрица системы, дополненная
столбцом свободных членов
a11 a12
a
a
21
22
A
am 1 am 2
a1n b1
a2 n b2
amn bm

6. Решение системы

Упорядоченное множество чисел (c1 ; c2 ; ; cn )
называется решением системы (1), если
каждое из уравнений системы обращается
в верное равенство после подстановки
вместо x1 , x2 , , xn соответственно чисел
(c1 ; c2 ; ; cn ).
Система
уравнений
называется
совместной, если она имеет хотя бы одно
решение. Система, не имеющая ни одного
решения, называется несовместной.

7.

Совместная
система
уравнений
называется определенной, если она имеет
единственное
решение,
и
неопределенной, если она имеет более
одного решения.
В последнем случае каждое ее решение
называется частным решением системы.
Совокупность всех частных решений
называется общим решением.

8.

Решить систему – это значит выяснить
совместна она или несовместна. Если
система совместна, найти ее общее
решение.
Две
системы
называются
эквивалентными, если они имеют одно и
то же общее решение.

9.

Система
линейных
уравнений
называется
однородной,
если
все
свободные члены равны нулю:
a11 x1 a12 x2
a x a x
m2 2
m1 1
a1n xn 0,
amn xn 0.
Однородная система всегда совместна,
x1 x2 xn 0 является
так как
решением
системы.
Это
решение
называется нулевым или тривиальным.

10. 6.2. Решение невырожденных линейных систем. Формулы Крамера

Рассмотрим систему n
уравнений с n неизвестными
a11 x1 a12 x2
a x a x
n2 2
n1 1
линейных
a1n xn b1 ,
ann xn bn .
Данная система может быть записана в
матричной форме: AX B.

11.

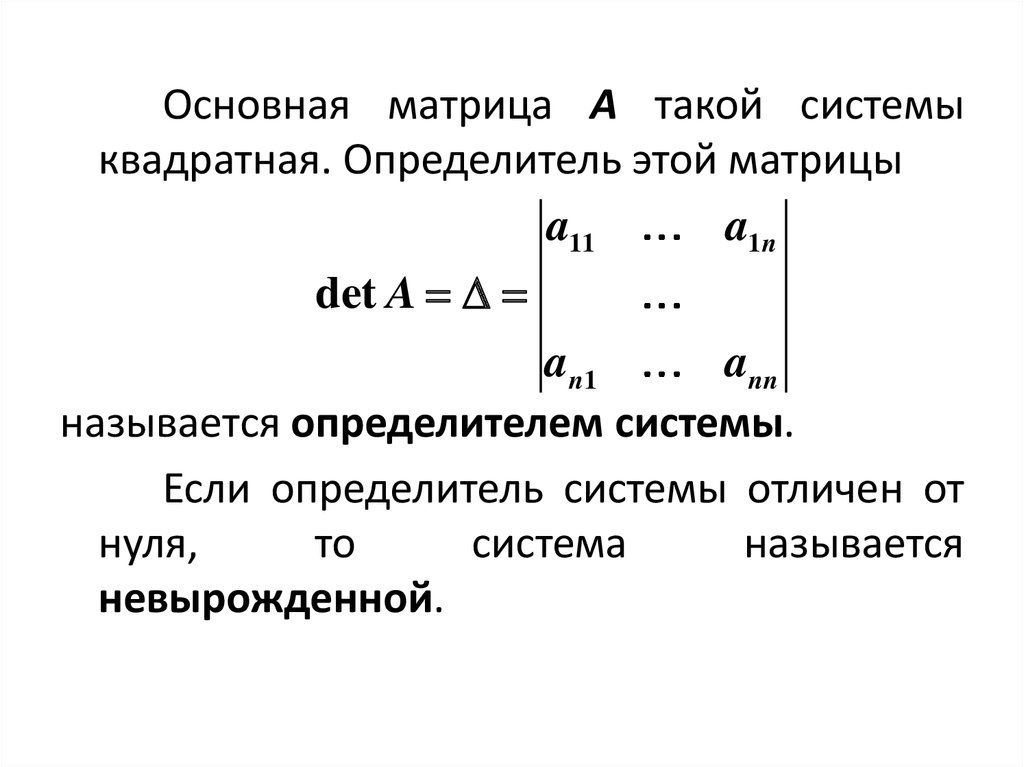
Основная матрица A такой системы
квадратная. Определитель этой матрицы
a11
a1n
det A
a n1
ann
называется определителем системы.
Если определитель системы отличен от
нуля,
то
система
называется
невырожденной.

12. Решение системы трех уравнений с тремя неизвестными

Система трёх уравнений
неизвестными имеет вид
a11 x a12 y a13 z b1 ,
a21 x a22 y a23 z b2 ,
a x a y a z b .
32
33
3
31
с
(2)
тремя

13.

Определитель системы
a11
a21
a12
a22
a13
a23 .
a31
a32
a33
Вспомогательные определители x , y , z :
b1
x b2
a12
a22
b3
a32
a13
a11
a23 , y a21
a33
a31
a11
z a21
a31
a12
a22
a32
b1
b2 .
b3
b1
b2
b3
a13
a23 ,
a33

14.

Система (2) может быть представлена в
x x ,
виде
y y ,
z z.
Откуда следует, что при 0 система
(2) имеет единственное решение, которое
находится по формулам Крамера:
x
x
,
y
y
,
z
z
.

15.

При 0 и хотя бы одном из x , y , z
отличном от нуля система (2) несовместна.
При
x y z 0
система
(2)
имеет
бесчисленное
множество решений.

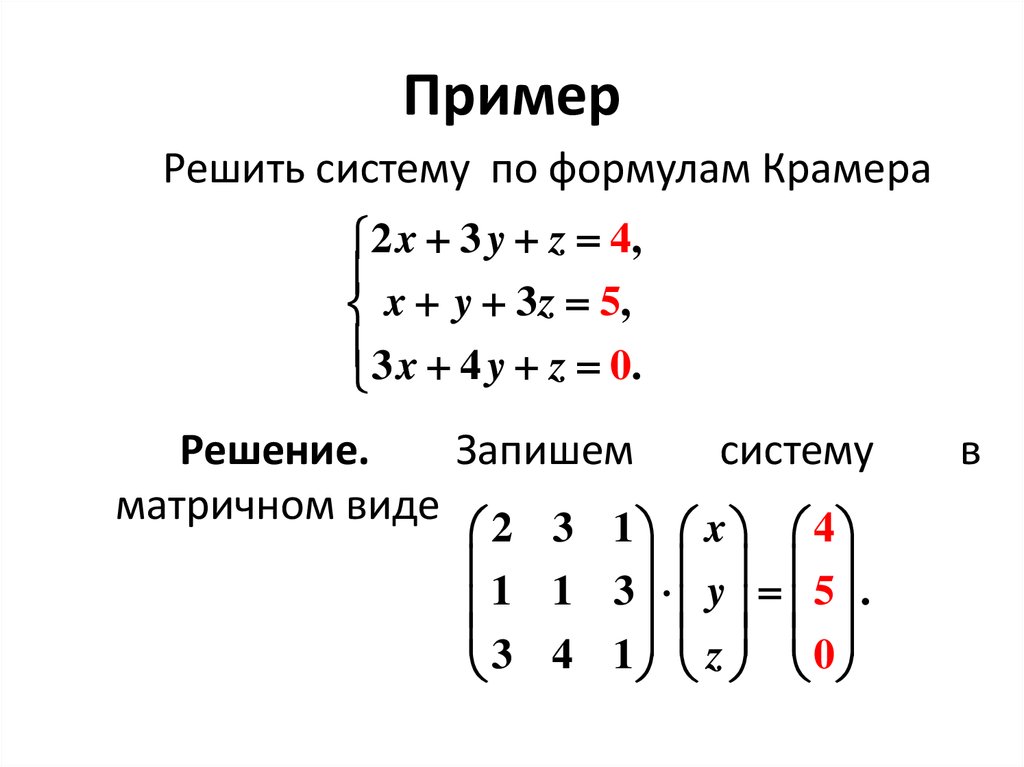
16. Пример

Решить систему по формулам Крамера
2 x 3 y z 4,
x y 3 z 5,
3 x 4 y z 0.
Решение.
Запишем
матричном виде 2 3 1
систему
x 4
1 1 3 y 5 .
3 4 1 z 0
в

17.

Найдем определитель системы
2 3 1
1 3
1 3
1 1
1 1 3 2
3
1
4 1
3 1
3 4
3 4 1
2 (1 12) 3 (1 9) 1 (4 3) 22 24 1 3 0
Так как определитель системы отличен от
нуля,
то система имеет единственное
решение.

18.

Вычислим x , y , z :
4 3 1
1 3
5 3
5 1
x 5 1 3 4
3
1
4 1
0 1
0 4
0 4 1
4 (1 12) 3 (5 0) 1 (20 0) 44 15 20 39
2 4 1
5 3
1 3
1 5
y 1 5 3 2
4
1
0 1
3 1
3 0
3 0 1
2 (5 0) 4 (1 9) 1 (0 15) 10 32 15 27

19.

2 3 4
1 5
1 5
1 1
z 1 1 5 2
3
4
4 0
3 0
3 4
3 4 0
2 (0 20) 3 (0 15) 4 (4 3) 40 45 4 9
По формулам Крамера находим
x 39
y 27
z 9
x
13, y
9, z
3.
3
3
3
Ответ: 13;9;3 .

20. 6.3. Исследование и решение СЛАУ. Теорема Кронекера-Капелли

Рассмотрим произвольную СЛАУ (1)
содержащую
m уравнений
и n
неизвестных.
Теорема 6.1. СЛАУ совместна тогда и
только тогда, когда ранг расширенной
матрицы системы равен рангу основной
матрицы:
rank A rankA.

21.

Теорема 6.2. Если ранг совместной
системы равен числу неизвестных, то
система имеет единственное решение.
Если ранг совместной системы меньше
числа неизвестных, то система имеет
бесчисленное множество решений.

22. 6.4. Метод Гаусса

Метод
Гаусса
(или
метод
последовательного
исключения
неизвестных) является универсальным
методом решения систем линейных
алгебраических уравнений.

23.

С
помощью
элементарных
преобразований
система
уравнение
приводится к равносильной системе
ступенчатого
вида,
из
которой
последовательно, начиная с последних (по
номеру) переменных находятся все
остальные переменные.

24.

Процесс решения по методу Гаусса состоит из
двух этапов:
1. На первом этапе (прямой ход) система
приводится к ступенчатому виду.
2. На втором этапе (обратный ход) идет
последовательное
определение
неизвестных из полученной ступенчатой
системы.

25. Элементарные преобразования

1. Перестановка уравнений местами.
2. Умножение
какого-либо
уравнения
системы на число, отличное от нуля.
3. Умножение
какого-либо
уравнения
системы на число, отличное от нуля и
прибавление
его
к
какому-либо
уравнению системы.

26.

Рассмотрим метод Гаусса для системы
третьего порядка, определитель которой не
равен нулю:
a11x1 a12 x2 a13 x3 b1 ,
a21x1 a22 x2 a23 x3 b2 ,
a x a x a x b .
31 1 32 2 33 3 3

27.

Исключим x1 из второго и третьего
уравнений,
используя
элементарные
преобразования системы а затем в
полученной системе исключим x2 из
третьего уравнения. Мы приведем систему
к «треугольному» виду:
a11x1 a12 x2 a13 x3 b1 ,
c22 x2 c23 x3 d 2 ,
c33 x3 d3.

28.

После этого начинается обратный ход
метода Гаусса: из последнего уравнения
находим x3 , из второго - x2 , из первого - x1 .
Замечание. Если коэффициент a11 в
системе равен нулю, то можно поменять
местами уравнения или неизвестные.

29.

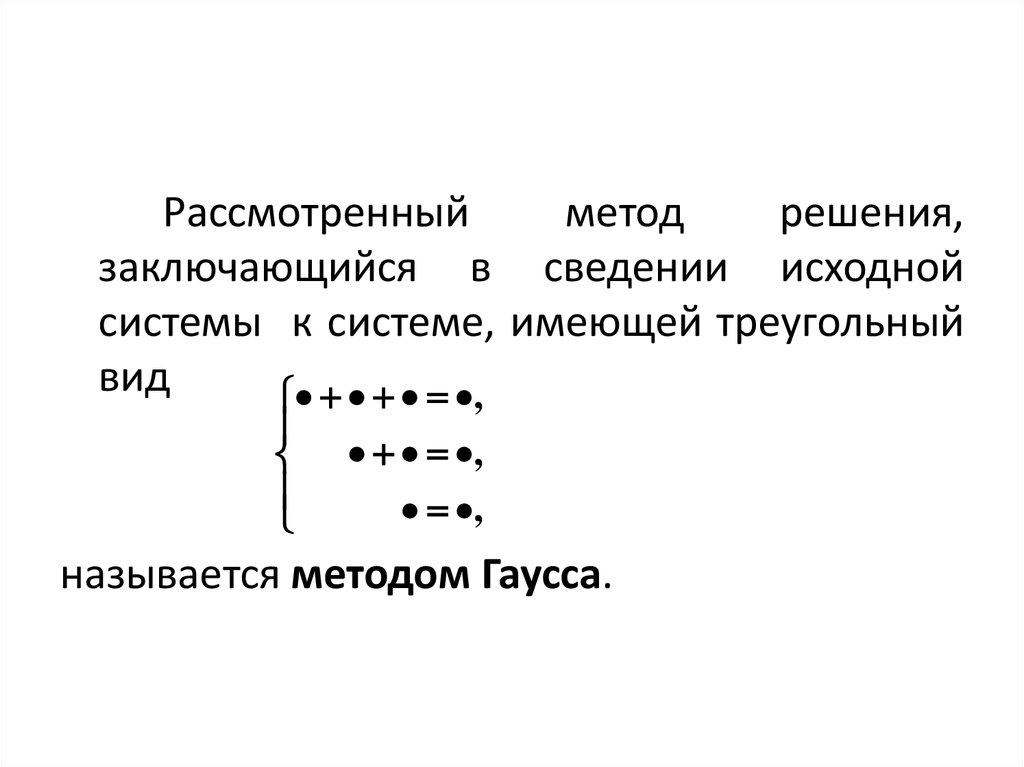
Рассмотренный
метод
решения,
заключающийся в сведении исходной
системы к системе, имеющей треугольный
вид
,
,
,
называется методом Гаусса.

30. Пример

Рассмотрим систему
x y 3 z 5,
2 x 3 y z 4,
3 x 4 y z 0.

31.

Исключим x из второго и третьего
уравнения. Для этого первое уравнение
умножим на –2 и сложим со вторым, затем
первое уравнение умножим на –3 и сложим
с третьим.
x y 3 z 5, ( 2)
2 x 3 y z 4,
3 x 4 y z 0.
2 x 2 y 6 z 10
2x 3 y z 4
y 7 z 6
( 3)
3 x 3 y 9 z 15
3x 4 y z 0
y 8 z 15

32.

Получим систему, равносильную данной:
x y 3 z 5,
y 7 z 6, ( 1)
y 8 z 15.
Далее исключим y из третьего
уравнения, для чего второе уравнение
полученной системы умножим на –1 и
сложим с третьим. Получим систему
x y 3 z 5,
y 7 z 6,
z 9.

33.

Из третьего уравнения z 9, подставим
во второе y 7 9 6
и найдем y 57.
Подставив найденные значения z 9 и
y 57 в первое уравнение x 57 3 9 5
получим x 79.
Ответ: 79;57;9 .

34. Пример

Решить систему методом Гаусса
3 x 4 y z 7,
x 2 y 3 z 0,
7 x 10 y 5 z 2.
Решение. Поменяем местами первое и
второе уравнения системы (т. к. удобно
иметь коэффициент при равный 1):
x 2 y 3 z 0, ( 3); ( 7)
3 x 4 y z 7,
7 x 10 y 5 z 2.

35.

x 2 y 3 z 0,
Получим систему 2 y 8 z 7, ( 2)
4 y 16 z 2.
x 2 y 3 z 0,
2 y 8 z 7,
0 12,
Последнее равенство неверно.
Следовательно, система несовместна.
.
Ответ:

36. Пример

2 x 3 y 1,
Решить систему методом Гаусса
4 x 6 y 2.
Решение. Умножим первое уравнение
на (-2) и сложим со вторым:
4 x 6 y 2
4x 6 y 2
0 0
Таким образом, в системе остается одно
уравнение 2 x 3 y 1.

37.

Такая система имеет бесчисленное
множество решений. Эти решения можно
записать в виде:
1 3c
y c, x
,
2
1 3
x c,
2 2
y c,
c

38. Пример

1. Установить, совместна ли система и,
если она совместна, найти ее решение по
формулам Крамера.
3x 2 y 5,
4 x 5 y 2,

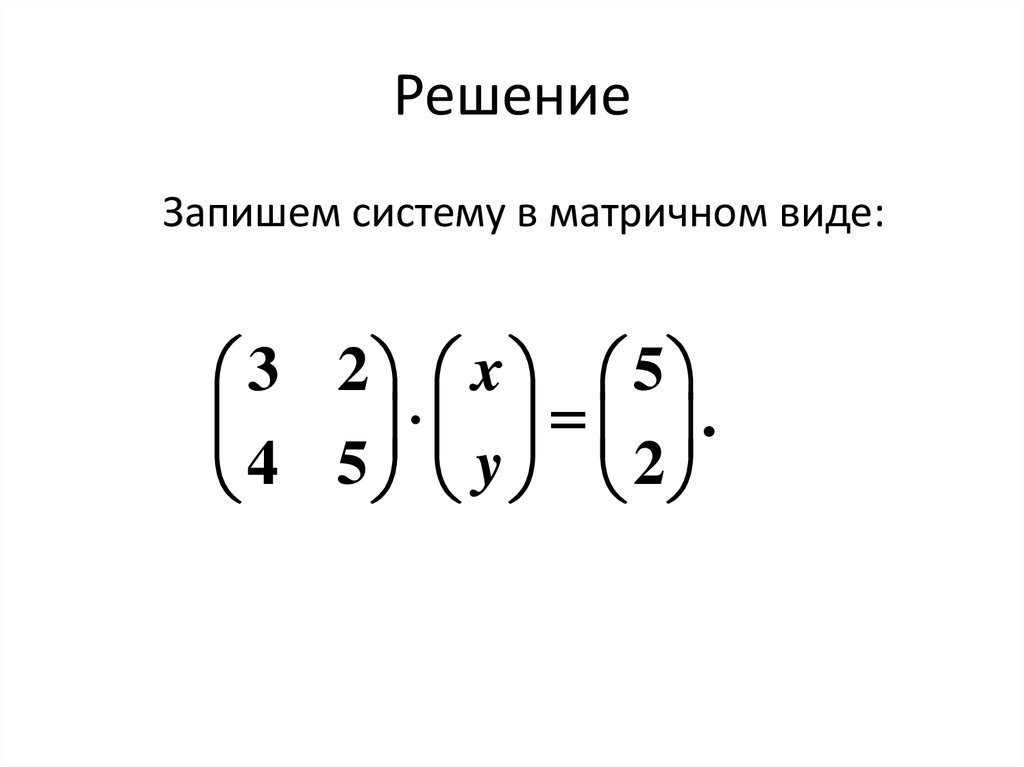
39. Решение

Запишем систему в матричном виде:
3 2 x 5
.
4 5 y 2

40.

Определитель системы равен
3 2
4 5
15 8 7 0
Следовательно, система имеет
единственное решение. Так как
1
то
5 2
2 5
25 4 21,
1 21
x 3,
7
Ответ: (3; 2)
2
3 5
14,
4 2
2
14
y
2.
7

41.

Найденное решение (3; 2) - это точка
пересечения прямых
3x 2 y 5 и 4 x 5 y 2

42.

2. Установить, совместна ли система и, если
она совместна, найти ее решение по
формулам Крамера.
2 x 3 y 1,
4 x 6 y 8,
Решение. Запишем систему в матричном
виде:
2 3 x 1
.
4 6 y 8

43.

Определитель системы:
2 3
4 6
12 12 0.
Определитель
x
1 3
6 24 18 0,
8 6
отличен от нуля, следовательно система
несовместна (т.е. не имеет решений).

44.

Так как каждое уравнение системы – это
уравнение прямой и система не имеет
решения, то это значит, что прямые
2x 3 y 1 и 4x 6 y 8
параллельны и не имеют общих точек.

45. Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ на плоскости

Тема: АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ НА ПЛОСКОСТИ

46.

Линия на плоскости часто задается как
множество точек, обладающих некоторым
только им присущим геометрическим
свойством.
Замечание: геометрическим образом
заданного уравнения не всегда является
линия.
2
2
x y 1

47.

ОПР. Уравнением линии (или кривой)
на плоскости Оху называется такое
уравнение F ( x; y ) 0 с
двумя
переменными, которому удовлетворяют
координаты x и y каждой точки линии и не
удовлетворяют координаты любой точки,
не лежащей на этой линии.
ОПР. Переменные x и y в уравнении
линии
называются
текущими
координатами точек линии.

48. §1. Уравнения прямой на плоскости

Простейшей из линий является прямая.
Каждая прямая на плоскости OXY
определяется уравнением первой степени с
двумя неизвестными.
Обратно: каждое линейное уравнение
первого порядка с двумя неизвестными
определяет
некоторую
прямую
на
плоскости.

49. 1.1. Различные виды уравнений прямой

Уравнение Ax By C 0, A 2 B 2 0
называется общим уравнением прямой.
Каждая прямая на плоскости Oxy
определяется линейным уравнением
первой степени с двумя неизвестными вида
Ax By C 0,
A
2
B2 0
и каждое линейное уравнение определяет
некоторую прямую.

50. Уравнение прямой в отрезках

Пусть дана прямая Ax By C 0 . Если
A B C 0 , то, разделив на ( C ):
A
B
x
y 1 0,
C
C
x
y
1,
C C
A
B
C
C
Обозначив a , b ,
A
B
x y
Получим a b 1
уравнение прямой в
отрезках; a и b – отрезки, которые она
отсекает на осях координат.

51. Пример

Записать уравнение прямой 2 x 6 y 12 0
в отрезках. Построить прямую.
y
Решение. 2 x 6 y 12
2 x 6 y 12
,
12 12 12
x y
1
6 2
0
2
6
x

52. Уравнение прямой с угловым коэффициентом k

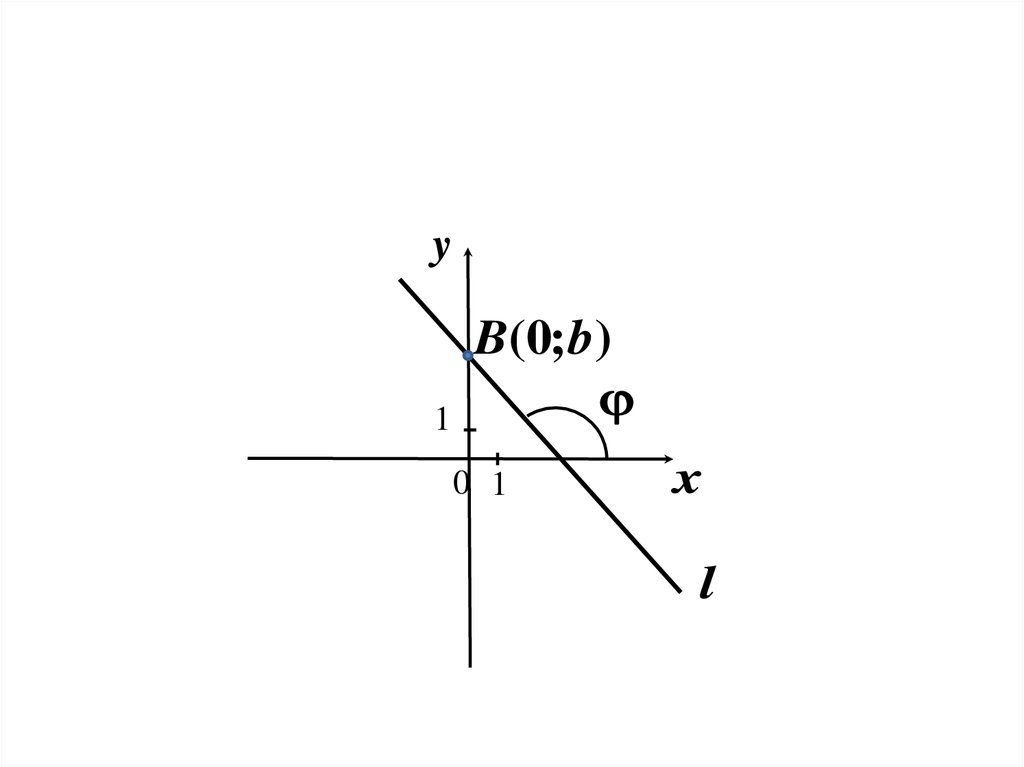
Дана прямая l , которая пересекает оси
координат и не параллельна ни одной из
них. Пусть угол наклона к положительному
направлению оси Ox равен
. Точка
пересечения с Oy – B(0; b) .

53.

y
1
B(0; b)
0 1
x
l

54.

Пусть M ( x; y ) – произвольная точка прямой.
y kx b
– уравнение прямой с
угловым коэффициентом k , где k tg .
Частные случаи:
1). k 0, y b – уравнение прямой,
параллельной оси Ох и отстоящей от нее на ;
2). b 0, y kx – прямая проходит через b
начало координат;
3). y 0
– уравнение оси Ox;
4).
x 0
– уравнение оси Oy;
5). x a – уравнение прямой, параллельной оси Oy и отстоящей от нее на a ;

55. Уравнение прямой, проходящей через данную точку в данном направлении k

Уравнение прямой, проходящей через
данную точку M ( x1 , y1 )
в данном направлении k
Пусть дана точка M ( x1 , y1 ) и задан угловой
коэффициент k. Тогда уравнение прямой
имеет вид:
y k ( x x1 ) y1 .

56. Уравнение прямой, проходящей через две данные точки и

Уравнение прямой, проходящей через две
данные точки M1 ( x1 ; y1 ) и
M 2 ( x 2 ; y2 )
y y1 y2 y1
x x1 x2 x1

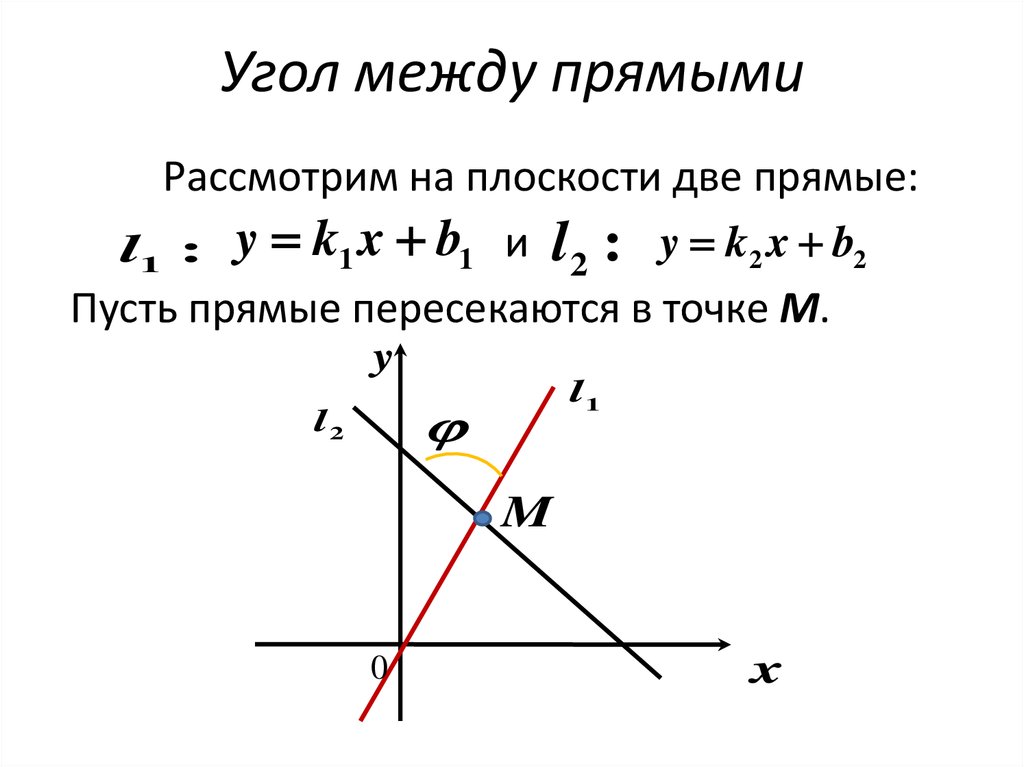
57. Угол между прямыми

Рассмотрим на плоскости две прямые:
l1 : y k1 x b1 и l 2 : y k2 x b2
Пусть прямые пересекаются в точке M.
y
l1
l2
M
0
x

58.

Углом между прямыми l1 и l 2 будем
называть наименьший угол, на который
надо повернуть l1 вокруг точки M против
часовой стрелки до совпадения ее со
второй прямой l 2 .

59.

Угол между прямыми: tg k2 k1
1 k2 k1
Взаимное расположение двух прямых:
k1 k2 ,
1. Прямые совпадают:
b1 b2 ,
k1 k2 ,
2. Прямые параллельны: b b ,
1
2
1
3. Перпендикулярны: k1
k2

60. Расстояние от точки до прямой

Расстояние d от точки M 0 ( x0 ; y 0 ) до
прямой Ax By C 0
d
d
M 0 ( x 0 ; y0 )
Ax0 By0 C
A B
2
2
.
Ax By C 0

61. Тема: Элементы векторной алгебры

62. §1. Векторы 1.1. Основные понятия

Величины,
которые
полностью
определяются своим численным значением,
называются
скалярными.
Примерами
скалярных величин являются: площадь, длина,
объем, температура, работа, масса.
Другие
величины,
например
сила,
скорость, ускорение, определяются не только
своим
числовым
значением,
но
и
направлением.
Такие величины называют векторными.
Векторная
величина
геометрически
изображается с помощью вектора.

63.

ОПР.
Вектором
называется
направленный отрезок.
На чертеже вектор изображается
отрезком, на котором стрелкой помечено
направление
a

64.

Если один конец отрезка AB - точка A начало вектора, а точка B - конец вектора,
то вектор обозначается символом AB :
AB
A
B

65.

Расстояние между началом и концом
вектора называется его модулем (или
длиной). Модуль обозначается AB , a .
Вектор, начало и конец которого
совпадают, называется нулевым вектором,
обозначается 0 . Модуль нулевого вектора
равен 0, а направление не определено.
Вектор, длина которого равна единице,
называется единичным (или ортом),
обозначается e

66.

Векторы, лежащие на параллельных
прямых (или на одной прямой), называются
коллинеарными a || b .
Три вектора в пространстве называются
компланарными, если они лежат в одной
плоскости или в параллельных плоскостях.
a
b
a
b

67.

Два коллинеарных вектора называются
противоположными, если они имеют
равные модули и противоположное
направление. Вектор, противоположный
вектору a , обозначается a .
a
a

68. 1.2. Линейные операции над векторами

Линейными
операциями
над
векторами
называют
их
сложение,
вычитание, умножение вектора на число.
Суммой двух векторов a и b называется
вектор c , начало которого совпадает с
началом вектора a , а конец ― с концом
вектора b
, при условии, что начало
вектора b совмещено с концом вектора a .
Записывают c a b.

69.

Дано:
a
b
f
Правило треугольника:
a
b
c a b
Правило многоугольника:
a
d a b f
b
f

70. Умножение вектора на число

Произведением вектора a на число
называется вектор b a
, который
удовлетворяет условиям:
1) b λ a ;
2) a и b ― одинаково направлены при λ 0;
3) a и b ― противоположно направлены при
λ<0.

71.

Дано:
- некоторое число;
a
1
a, λ 0
2
λa, λ 0
3a, λ 0

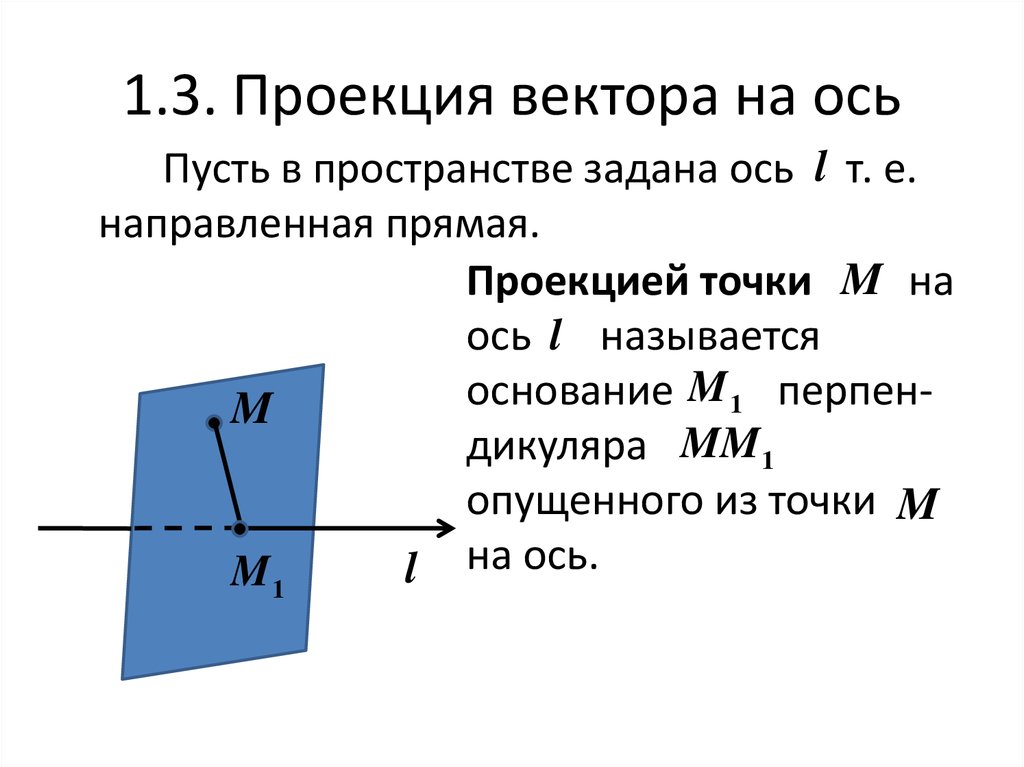
72. 1.3. Проекция вектора на ось

Пусть в пространстве задана ось l т. е.
направленная прямая.
Проекцией точки M на
ось l называется
M
основание
1 перпенM
дикуляра MM1
опущенного из точки M
l на ось.
M1

73.

Если точка M лежит на оси, то ее проекция
на ось совпадает с самой точкой.
Пусть AB 0 — произвольный вектор.
Обозначим через A1 и B1 проекции на ось
соответственно начала и конца вектора
AB и рассмотрим вектор A1 B1 .
ОПР. Проекцией вектора AB на ось
называется положительное число A1 B1 ,
если вектор A1 B1 и
ось
одинаково
направлены и отрицательное число A1 B1 ,
если вектор A1 B1 и ось противоположно
направлены.

74.

Если точки A1 и B1 совпадают, то проекция
вектора A1 B1 равна 0.
Проекция вектора A1 B1 на ось l
обозначается: прl AB .
Угол между вектором a и осью l
(или угол между двумя векторами)
изображен на рисунке
a
l

75. 1.4. Линейная зависимость векторов

При решении различных задач, как
правило, приходится иметь дело не с
одним
вектором,
а
с
некоторой
совокупностью
векторов
одной
размерности. Такую совокупность векторов
называют
системой
векторов
и
обозначают:
a1 , a2 ,
, an .
(1)

76.

ОПР. Линейной комбинацией векторов
(1) называется вектор вида
b 1 a1 2 a2 n an ,
где 1 , 2 , , n –
любые
действительные числа. В этом случае говорят
также, что вектор b линейно выражается
через векторы a1 , a2 , , an .

77.

ОПР. Система ненулевых векторов (1)
называется линейно зависимой, если
существую такие числа , , ,
, не
1
2
n
равные одновременно нулю, что линейная
комбинация данной системы с указанными
числами равна нулевому вектору:
1 a1 2 a2 n an 0. (2)
Если же равенство (2) для данной
системы векторов выполняется лишь при
1 2 n 0
то такая система векторов называется
линейно независимой.

78.

ОПР. Размерностью системы векторов
называется
максимальное
число
содержащихся в нем линейно независимых
векторов.
Если таких векторов n, то система
называется n-мерной.
ОПР. Совокупность n линейно независимых
векторов n -мерной системы векторов (1)
называется ее базисом.

79.

Теорема Каждый вектор b n-мерной
системы векторов можно представить и
притом единственным способом в виде
линейной комбинации векторов базиса
b 1 a1 2 a2 n an , (3)
Равенство (3) называется разложением
вектора b по базису a1 , a2 , , an , а числа
1 , 2 , , n – координатами вектора b
относительно этого базиса.

80.

В силу единственности разложения (3)
каждый вектор однозначно может быть
определен координатами в некотором
базисе.
На
плоскости
любые
два
неколлинеарных вектора образуют базис.
В
пространстве
любые
три
некомпланарных вектора образуют базис.

81. 1.5. Координаты вектора

Координатами вектора a в прямоугольной
системе координат
OXY называются
проекции x, y, вектора a на оси координат.
Обозначают a ( x , y ).
y
M ( x; y)
yj
a
j
0i
xi
x

82.

Множество всех n-мерных векторов с
действительными
координатами
n
обозначается R .
2
a
(
x
,
y
)
R
.
Таким образом, вектор

83.

Если i , j – единичные векторы (орты)
координатных осей, то вектор
можно
представить в виде a xi y j .
Направляющими косинусами вектора a
называются косинусы углов
, ,
образуемых им с осями координат OX и OY
соответственно.
cos
cos
x
a
y
a
x
x y
2
2
y
x y
2
2

84.

Если вектор a имеет начало в точке A x1 ; y1
и конец в точке B x2 ; y2 , то координаты
вектора
равны разности соответствующих координат конечной и начальной его
точек: a AB x2 x1; y2 y1
Модуль вектора AB
AB
x2 x1
2
y2 y1 .
2

85. Пример

Даны точки A 1;2 и
B 5;4 .
Найти: а) координаты AB;
б) модуль AB .
Решение. а) Координаты AB (5 1;4 2) (4;2)
б) Модуль найдем, используя формулу
AB
x2 x1
2
y2 y1 .
2
AB 42 22 20 2 5.

86. 1.6. Действия над векторами, заданными координатами

Пусть a x1; y1 , b x2 ; y2 .
тогда
a b x1 x2 ; y1 y2
a x1; y1
a b x1 x2 , y1 y2 .

87.

Условие параллельности векторов
aи b
x1 y1
a || b
x2 y2
Условие перпендикулярности векторов
a и b
a b x1 x2 y1 y2 0

88. 1.7. Скалярное произведение векторов

ОПР. Скалярным произведением векторов
a и b называется число, равное произведению их модулей на косинус угла между
ними:
a b a b cos .
Если известны координаты векторов
то
скалярное произведение
вычислить по формуле
aи b
можно
a b x1 x2 y1 y2 .

89. Свойства скалярного произведения:

1). a b b a;
2). a b a b ;
3).
a b c a c b c;
2
4).
2
a a a a .

90. Угол между векторами:

cos
a b
;
a b
a
b
Условие перпендикулярности векторов:
a b 0 a b
если
a и b ― ненулевые векторы.

91. Пример

Найти скалярное произведение векторов
И b , если угол между ними равен 60°,
a 2, b 3.
Решение. Так как a b a b cos ,
то
1
a b 2 3 cos60 6 3
2
a

92.

Рассмотрим пространство
3
Вектор a ( x , y , z ) R .
Тогда a xi y j zk .
x2 x1
AB
cos
cos
x
a
z
a
2
3
R .
y2 y1 ( z2 z1 ).
2
x
x2 y2 z2
y
cos
a
z
x y z
2
2
2
y
x y z
2
2
2

93. Компланарность векторов

• Три вектора a x1 i y1 j z1 k ,
b x 2 i y2 j z 2 k ,
c x3 i y3 j z 3 k ,
компланарны тогда и только тогда, когда
x1
x2
y1
y2
z1
z2 0.
x3
y3
z3