Курс лекций по математике

1. Презентации по математике для специальности «Нефтегазовое дело» Составил старший преподаватель кафедры «Математики и информатики»: Кузн

Презентации по
математике
для специальности «Нефтегазовое дело»
Составил старший преподаватель кафедры
«Математики и информатики»:
Кузнецова
Ольга
Владимировна
(1 корпус, 17 каб.)

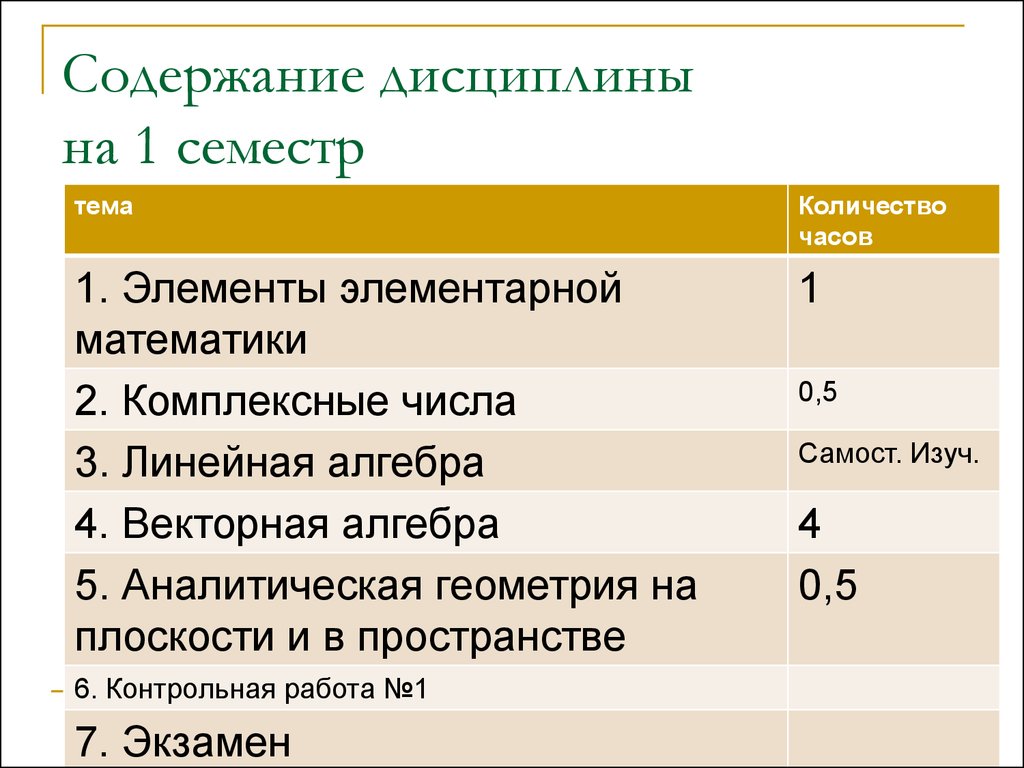
2. Содержание дисциплины на 1 семестр

тема
Количество
часов
1. Элементы элементарной
математики
2. Комплексные числа
3. Линейная алгебра
4. Векторная алгебра
5. Аналитическая геометрия на
плоскости и в пространстве
1
6. Контрольная работа №1
7. Экзамен
0,5
Самост. Изуч.
4
0,5

3. Информационные источники

1.
2.
3.
4.
5.
6.
Список литературы:
Шипачев В.С. «Высшей математики» - М.: «Высшая школа»,
2003.
Шипачев В.С «Задачник по высшей математике» - М.: «Высшая
школа», 2003
М.Я. Выгодский «Справочник по высшей математике» - М.:
«Высшая школа», 2000.
Гусак А.А. Справочное пособие к решению задач « - Минск,
НТООО «ТетраСистемс», 2001г.
«Высшая математика для экономистов» под. ред. Профессора
Кремера Н.Ш. – «Юнити» Москва 2000 г.
Зимина О.В., Кириллов А.И., Сальникова Т.А. «Решебник.
Высшая математика.» - М. Физматлит 2001г.

4. Информационные источники

Список литературы (электронный формат)
А.Б. Соболев, А.Ф. Рыбалко Математика: Курс лекций для
технических вузов. 1 и 2 части.
2. Ларин Александр Александрович “Курс высшей математики.
Часть1.”
3. Д. Т. Письменный Конспект лекций по высшей математике:
полный курс.
4. Математика в примерах и задачах. Журбенко Л.Н., Никонова
Г.А. и др.
5. Алгебра в таблицах. 7—11 кл. Справочное пособие. Звавич
Л.И., Рязановский А.Р.
Studens_tmp (общая папка для хранения метолдических,
контрольных материалов для студентов филиала УдГУ в
Воткинске) ftp://78.85.20.33
КузнецоваОВ=> Математика для НД => НД1курс
1.

5. Образовательные ресурсы интернета

1.
2.
3.
4.
5.
Поисковая система Нигма – математика,
Эл. адрес: http://nigma.ru;
Высшая математика – просто и доступно!
Эл. адрес: http://www.mathprofi.ru
Универсальный калькулятор.xls
Математический форум Math Help Planet
Эл. адрес http://mathhelpplanet.com
Интернет-тестирование, тренажеры,
методика, аналитика www.i-exam.ru

6. Образовательные ресурсы интернета

1.
2.
Образовательный проект А.Н. Варгина
http://www.ph4s.ru/
Образовательные ресурсы Интернета Математика. http://www.alleng.ru/

7. Программные приложения для математических вычислений

Mathcad - система компьютерной алгебры
(платная) ссылка на эл. ресурс
http://www.ptc.com/products/mathcad/
Maxima - свободная система
компьютерной алгебры ссылка на эл.
ресурс http://maxima.sourceforge.net/ru/,
http://sourceforge.net/projects/maxima/files/M
axima-Windows/5.25.0-Windows/maxima5.25.0.exe/download

8. Введение в математику

1.
Для того чтобы успешно решать задачи по
высшей математике НЕОБХОДИМО:
складывать, вычитать, умножать и делить
Вспомнить правила раскрытия скобок:
– здесь знаки у слагаемых не меняются
2.
– а здесь меняются на противоположные.
3.
И для умножения:
4.
ДВА МИНУСА ДАЮТ ПЛЮС, а ТРИ МИНУСА – ДАЮТ МИНУС

9. 1. Элементы элементарной математики

Вспоминаем, что дроби можно
сокращать(сократили на 2),
(сократили на 5)
х 1
2
х
х
(сократили на х).

10. 2. Комплексные числа 2.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Определение. Комплексным числом z
называется выражение
, где a и
z a ib
b – действительные числа,
i – мнимая единица:
2
i 1;
i 1.
При этом:
a действительная (a = Re z)
b- мнимая часть (b = Im z).

11.

Определение. Числа z a ib и z a ib
называются комплексно – сопряженными.
Определение. Два комплексных числа
называются
z1 a1 ib1 z 2и a 2 ib 2
равными, если соответственно равны их
действительные и мнимые части:
a1 a 2 ;
b1 b2 ;
Определение. Комплексное число равно
нулю, если соответственно равны нулю
действительная и мнимая части.
a b 0.

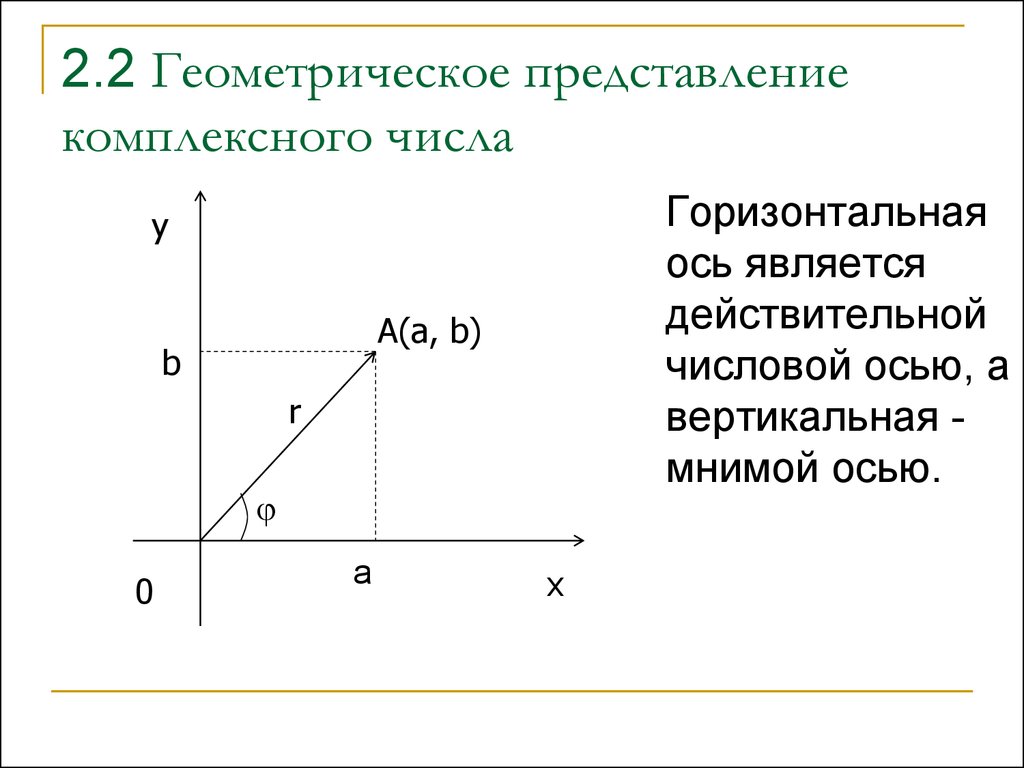
12. 2.2 Геометрическое представление комплексного числа

Горизонтальная
ось является
действительной
числовой осью, а
вертикальная мнимой осью.
у
A(a, b)
b
r
0
a
x

13. 2.3 Тригонометрическая форма комплексного числа.

Из геометрических соображений:
a r cos ; b r sin
Тогда комплексное число можно представить в виде:
z a ib r cos ir sin r (cos i sin )
- тригонометрическая форма записи к. ч.
Величина r - модуль комплексного числа,
угол наклона - аргумент комплексного числа.
Из геометрических соображений:
Для комплексно – сопряженных чисел:
r z;
Arg z
b
r a ib a b ; Arg z arctg ;
a
2
z z;
2
Arg z Arg z .

14. 2.4 Действия с комплексными числами.

Основные действия с комплексными
числами вытекают из действий с
многочленами
1) Сложение и вычитание.
z z1 z 2 ( a1 ib1 ) ( a 2 ib2 ) ( a1 a 2 ) i (b1 b2 )
z ( a1 a 2 ) 2 (b1 b2 ) 2

15.

2) Умножение
z z1 z 2 ( a1 ib1 )( a 2 ib 2 ) a1 a 2 ia1b2 ib1 a 2 i b1b2
2
z z1 z 2 ( a1a2 b1b2 ) i ( a1b2 b1a2 )
В тригонометрической форме:
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 ).
z z1 z 2 r1 r2 (cos( 1 2 ) i sin( 1 2 ))
В случае комплексно – сопряженных чисел:
2
2
zz ( a ib )( a ib ) a b z z .
2
2

16.

3) Деление.
a1a2 b1b2
a2b1 a1b2
z
i 2
2
2
a2 b2
a2 b22
(a1 ib1 )( a 2 ib 2 ) (a1 a 2 b1b2 ) i (a 2 b1 a1b2 )
z
(a 2 ib 2 )( a 2 ib 2 )
a 22 b22
В тригонометрической форме:
z1 r1
z
(cos( 1 2 ) i sin( 1 2 ))
z 2 r2

17.

4) Возведение в степень.
Из операции умножения:
z zz r (cos 2 i sin 2 )
2
2
В общем случае:
z r (cos n i sin n )
n
n
где n – целое положительное число.
Это выражение называется формулой
Муавра

18.

5) Извлечение корня из комплексного числа
n
2 k
2 k
z r (cos i sin ) r cos
i sin
n
n
где к=0, 1, 2, …, n-1
Корень n – ой степени из комплексного
числа имеет n различных значений.
n
n

19. 2.5 Показательная форма комплексного числа

Уравнение Эйлера:
w e
x iy
e (cos y i sin y )
x
Показательная форма к.ч.
z re
i

20. 3. Линейная алгебра

Самостоятельное изучение

21. 3. Векторная алгебра. 3.1 Определения

Совокупность всех направленных отрезков, для
которых введены операции:
- сравнения
- сложения
- умножения на вещественное число
называется множеством векторов.
Конкретный элемент этого множества будем
называть вектором и обозначать символом с
верхней стрелкой,
например a
a
c
b
d
l

22. Определения

Вектор определяется как направленный отрезок:
B
A
Точка А – начало вектора,
В – конец вектора.
Записывают:
AB
или
a.

23. Определения

Направленный отрезок, начало и конец которого
совпадают, называется нулевым направленным
отрезком.
0
A
Длиной (модулем) вектора называется
расстояние между началом и концом вектора.
АВ а

24.

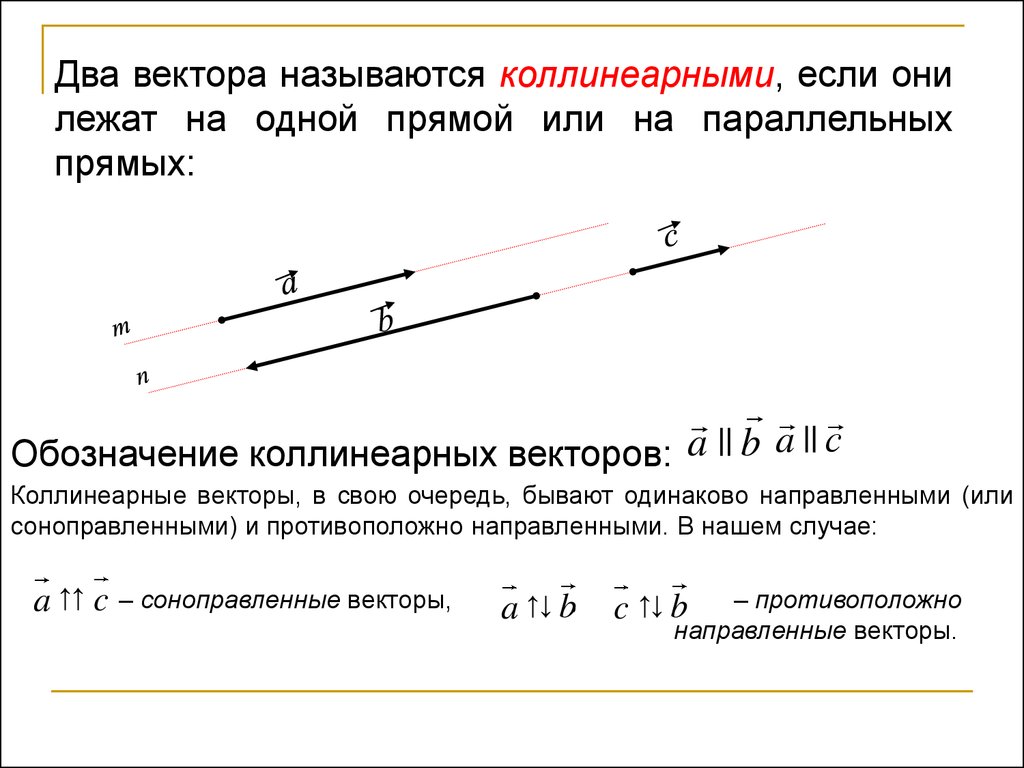
Два вектора называются коллинеарными, если они
лежат на одной прямой или на параллельных
прямых:
Обозначение коллинеарных векторов: a || b a || с
Коллинеарные векторы, в свою очередь, бывают одинаково направленными (или
соноправленными) и противоположно направленными. В нашем случае:
a ↑↑ c – соноправленные векторы,
a ↑↓ b,
– противоположно
направленные векторы.
c ↑↓ b

25. Определения

Три вектора, параллельные одной и той же
плоскости, называются компланарными.
Нулевой вектор считается коллинеарным любому
другому вектору. Нулевой вектор считается
компланарным любой паре векторов.
a
b
c

26. Определения

Два вектора называются равными, если:
1) они соноправлены;
2) их модули равны, т.е. a b a ↑↑ b è
a
b
a b

27. Определения

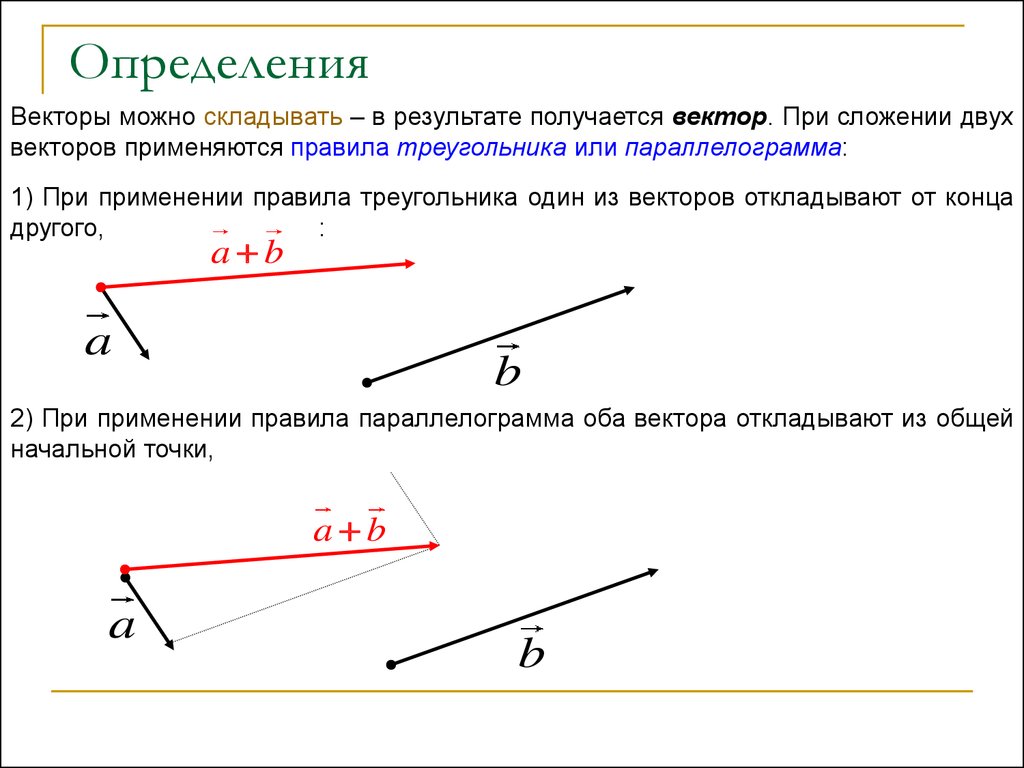
Векторы можно складывать – в результате получается вектор. При сложении двух
векторов применяются правила треугольника или параллелограмма:
1) При применении правила треугольника один из векторов откладывают от конца
другого,
:
a b
a
b
2) При применении правила параллелограмма оба вектора откладывают из общей
начальной точки,
a b
a
b

28.

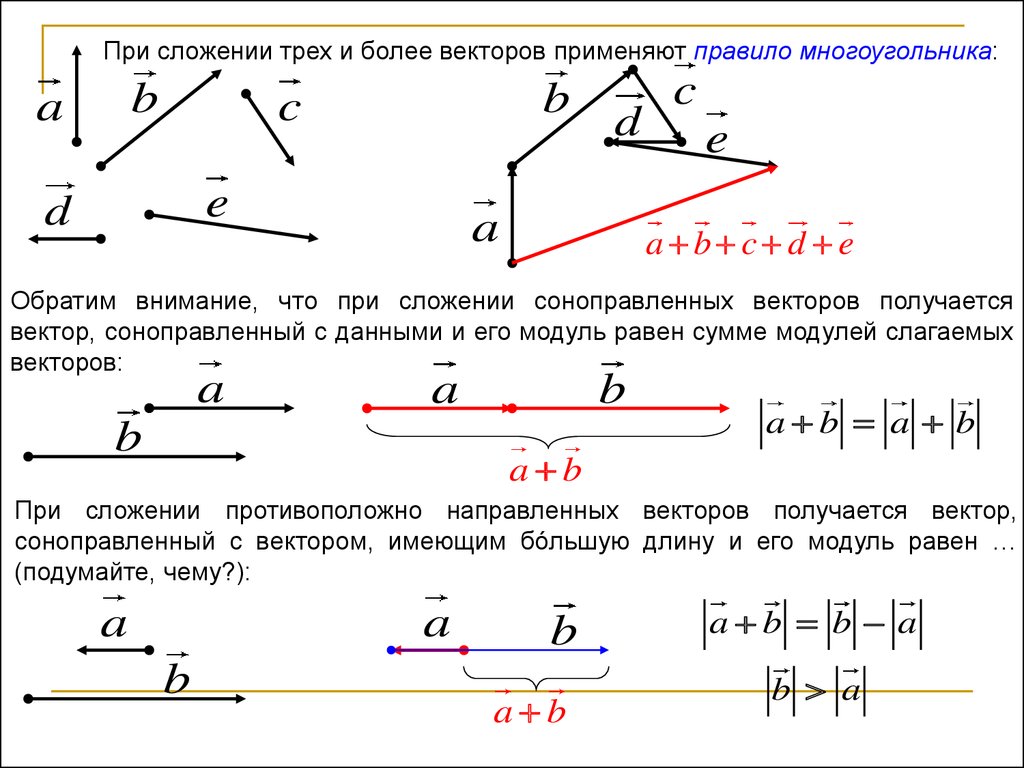
При сложении трех и более векторов применяют правило многоугольника:
b
a
b
c
e
d
d
a
c
e
a b c d e
Обратим внимание, что при сложении соноправленных векторов получается
вектор, соноправленный с данными и его модуль равен сумме модулей слагаемых
векторов:
a
a
b
b
a b a b
a b
При сложении противоположно направленных векторов получается вектор,
соноправленный с вектором, имеющим бóльшую длину и его модуль равен …
(подумайте, чему?):
a
a
b
b
a b
a b b a
b a

29.

Сложение векторов, как и сложение чисел подчиняется законам:
1)
a b b a
2)
a b c a b c – сочетательный закон сложения;
– переместительный закон сложения;
a 0 a ;
4) a a 0 .
3)
Следующее действие с векторами – умножение вектора на число k. В результате
этого действия получается вектор, причем:
1) если k>0, то
2) если k<0, то
k a ↑↑ a
k a ↑↓ a
ka k · a ;
и ka k · a ;
и
3) если k=0, то 0 ·a 0 .
8
a
3
3a
a
0·a
k=0
4
a
3
2a
k>0
k<0

30. Линейная зависимость векторов

Определение. Выражение вида
1 a1 2 a2 ... n an
, где i ; i [1, n]
некоторые числа, называется линейной
комбинацией векторов
a1 , a2 ,..., an

31. Линейная зависимость векторов

Определение. Векторы a1, a2 ,..., an
называются линейно зависимыми, если
существует ихn нетривиальная
линейная
n
комбинация k ak такая, что k ak o
k 1
k 1
Определение. Векторы a1, a2 ,..., an
называются
независимыми, если из
n линейно
k ak o следует
n
условия k
тривиальность
1
k ak
линейной комбинации k
1

32. Базис в пространстве векторов

Определение:
Базисом в пространстве векторов
называется набор линейно независимых
векторов

33. Базис в пространстве векторов

b
Определение
Базисом на прямой называется любой
ненулевой вектор, принадлежащий этой
прямой. m
a
3a
b 3a
l

34. Базис в пространстве векторов

Определение Базисом на плоскости называется
любая упорядоченная пара линейно
независимых векторов, принадлежащих этой
плоскости.
Определение Базисом в пространстве
называется любая упорядоченная тройка
линейно независимых векторов.
Определение Базис называется ортогональным,
если образующие его векторы попарно
ортогональны (взаимно перпендикулярны).
Определение Ортогональный базис называется
ортонормированным, если образующие его
векторы имеют единичную длину

35. Координаты вектора:

Пусть дан базис {g1, g 2 , g 3} тогда любой
вектор x в пространстве может
быть представлен, и притом
единственным образом, в виде
x g1 g 2 g 3
где , ,
- некоторые числа
(коэффициенты разложения), которые
называют координатами данного
вектора в заданном базисе.

36. Координаты вектора:

x g1 g 2 g 3
Для записи вектора
в координатном представлении
используются формы:
x( ; ; )
( ; ; )

37. Операции с векторами в координатном представлении:

Сравнение векторов: Два вектора и
равны тогда и только тогда, когда
равны их соответствующие
координаты
Сложение векторов : При сложении двух
векторов их соответствующие
координаты складываются.
Умножение вектора на число: При
умножении вектора на число, на это
число умножаются все координаты
вектора.

38. Условия линейной зависимости и независимости векторов в координатном представлении

Для того чтобы два вектора
x x1 g1 x2 g 2
y y1 g1 y 2 g 2
на плоскости были линейно зависимы,
необходимо и достаточно, чтобы их
координаты в некотором базисе
удовлетворяли условию
x1
det
y1
x2
0
y2

39. Условия линейной зависимости и независимости векторов в координатном представлении

x x1 g1 x2 g 2 x3 g 3
Для того чтобы три вектора
y y1 g1 y2 g 2 y3 g 3
z z1 g 1 z 2 g 2 z 3 g 3
в пространстве были линейно зависимы, необходимо
и достаточно, чтобы их координаты в некотором
базисе удовлетворяли условию
x1
det y1
x2
y2
x3
y3 0
z1
z2
z3

40. Замечание:

Равенства
x1
det
y1
x2
0
y2
и
x1
det y1
x2
y2
x3
y3 0
z1
z2
z3
соответственно являются
необходимыми и достаточными
условиями коллинеарности пары
векторов на плоскости и
компланарности тройки векторов в
пространстве.

41. Декартова система координат.

Определение. Декартовой системой координат в
пространстве называется совокупность точки и
базиса. Точка называется началом координат.
Прямые, проходящие через начало координат
называются осями координат.
1-я ось – ось абсцисс
2-я ось – ось ординат
3-я ось – ось апликат
Определение. Декартова система координат, базис
которой ортонормирован называется декартовой
прямоугольной системой координат. Будем
обозначать векторы базиса . i , j , k

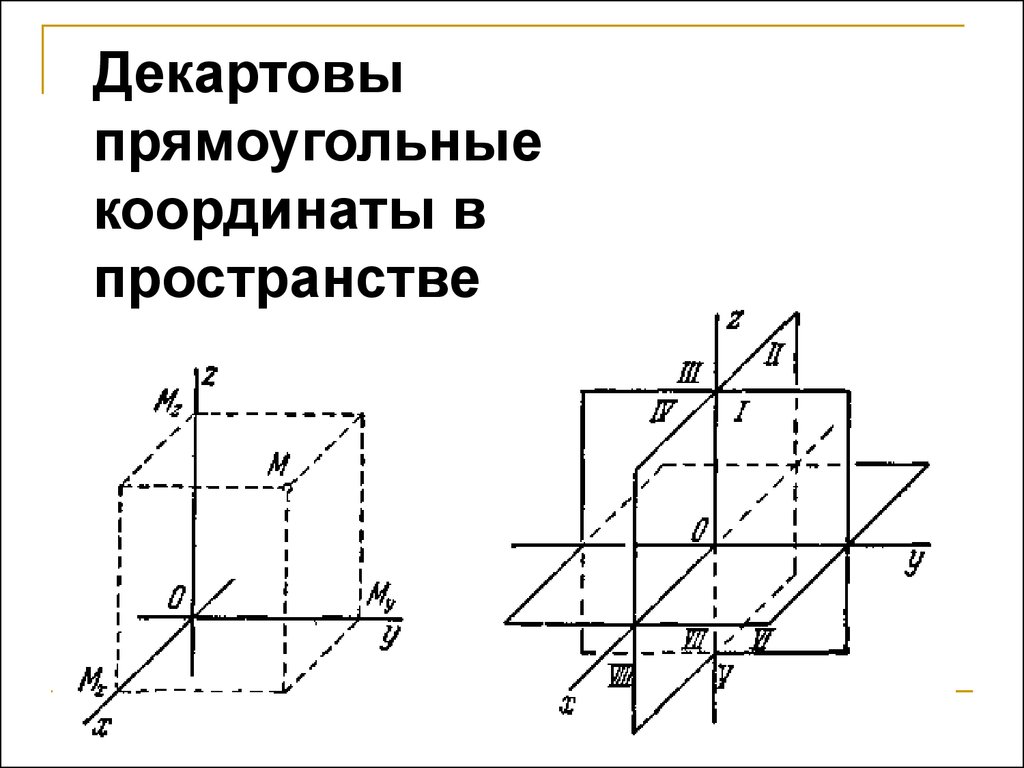
42.

Декартовы
прямоугольные
координаты в
пространстве

43. Основные формулы:

Если заданы точки А(x1, y1, z1), B(x2, y2, z2), то
координаты вектора определяются по формуле:
АВ = (x2 – x1, y2 – y1, z2 – z1).
Длина вектора в координатах определяется как
расстояние между точками начала и конца вектора.
Если заданы две точки в пространстве
А(х1, y1, z1), B(x2, y2, z2), то:
AB ( x2 x1 ) 2 ( y 2 y1 ) 2 ( z 2 z1 ) 2

44. Основные формулы:

Если точка М(х, у, z) делит отрезок АВ в
соотношении / , считая от А, то координаты
этой точки определяются как:
x1 x2
x
;
y1 y 2
z1 z 2
y
; z
.
В частном случае координаты середины
отрезка находятся как:
x = (x1 + x2)/2; y = (y1 + y2)/2; z = (z1 + z2)/2.

45. Скалярное произведение векторов.

Определение. Скалярным
произведением векторов и называется
число, равное произведению длин этих
сторон на косинус угла
между ними.
a b = a b cos
Если рассматривать векторы
a( xa , y a , z a ); b( xb , yb , z b )
в декартовой прямоугольной системе координат, то
a
b = x a x b + y a y b + z a z b;

46. Формула для вычисления угла между векторами:

x a xb y a y b z a z b
cos
a b

47. Свойства скалярного произведения векторов

1) a a
a 2;
=
2) a b = 0, если a b
a = 0 или
или
3) a b = b a
;
b
a c ;
4) a ( b + c ) = a b +
5) (m a ) b =
(
m) = m(
m=const
a b
= 0.
a b
);

48. Векторное произведение векторов.

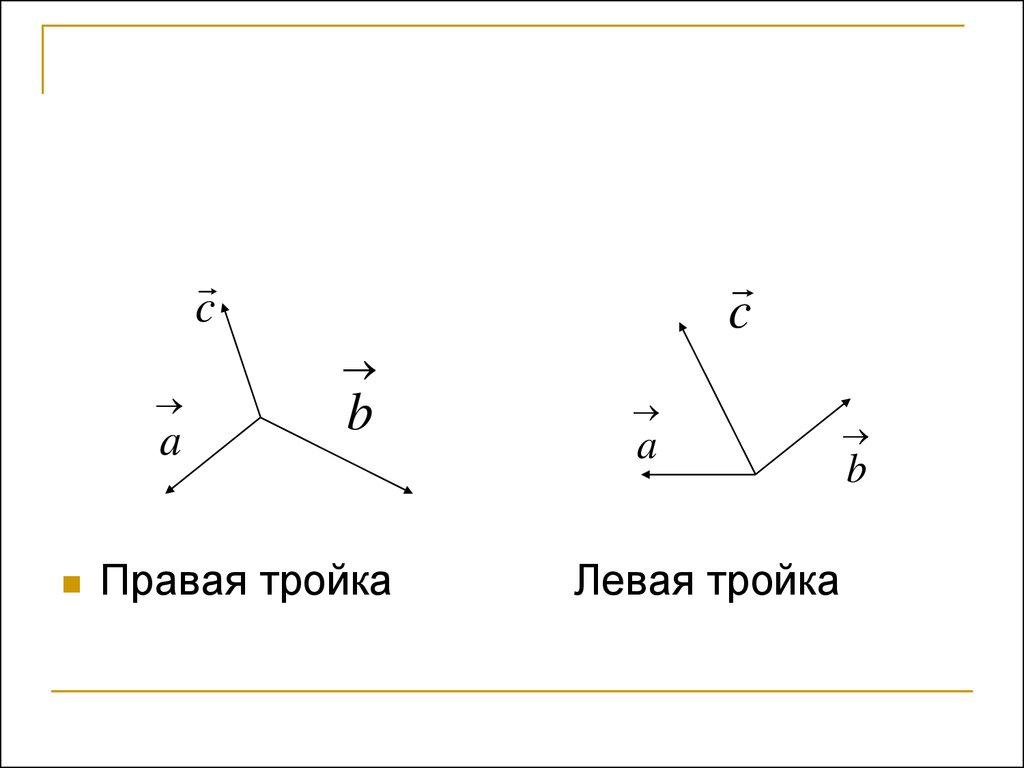
c
b
взятые в указанном порядке образуют
Три некомпланарных вектора
a
правую тройку, если с конца третьего
вектора кратчайший поворот от
первого вектора ко второму виден
совершающимся против часовой
стрелки, и левую - если по часовой.

49.

c
c
a
b
Правая тройка
a
Левая тройка
b

50. Векторное произведение векторов.

Векторным
произведением векторов
a и b называется вектор c
удовлетворяющий следующим условиям:
1) c a b sin где - угол между векторами
sin 0; 0
2) вектор c ортогонален векторам a и
3) a b c образуют правую тройку
векторов.
b

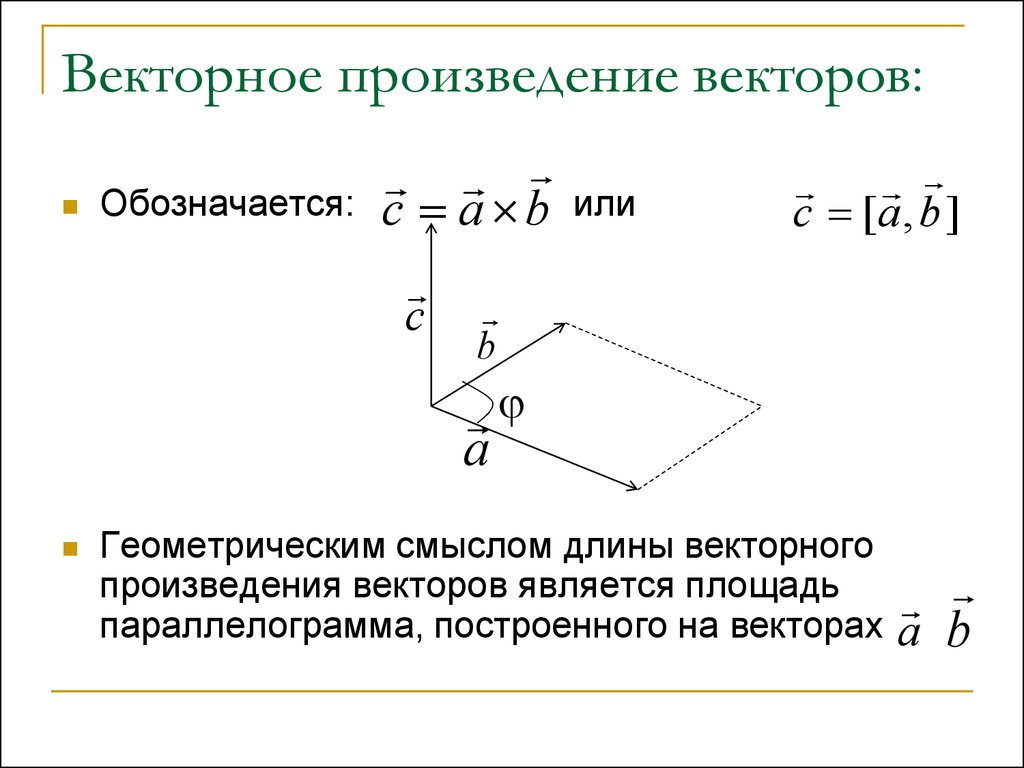
51. Векторное произведение векторов:

Обозначается:
c a b
c
или
c [a , b ]
b
a
Геометрическим смыслом длины векторного
произведения векторов является площадь
параллелограмма, построенного на векторах
a b

52. Свойства векторного произведения векторов:

1)
b a a b ;
2) a b 0, если a b
или a = 0 или
3) (m )
=
4)
(
+
b = 0;
(m b ) = m(
b );
a
a
a
b
a b с ) = a b + a с;

53. Векторное произведение векторов

Если заданы векторы
(x , y , z ) и (x , y , z )
b b b b
a a a a
в декартовой прямоугольной
системе
координат
с
единичными векторами i , j , k , то
c a b
=
i
j
k
xa
xb
ya
yb
za
zb

54. Смешанное произведение векторов.

Определение. Смешанным
произведением векторов a , b и c
называется число, равное скалярному
произведению вектора a на вектор,
равный векторному
произведению
векторов b и c
Обозначается a b c или ( a , b , c )

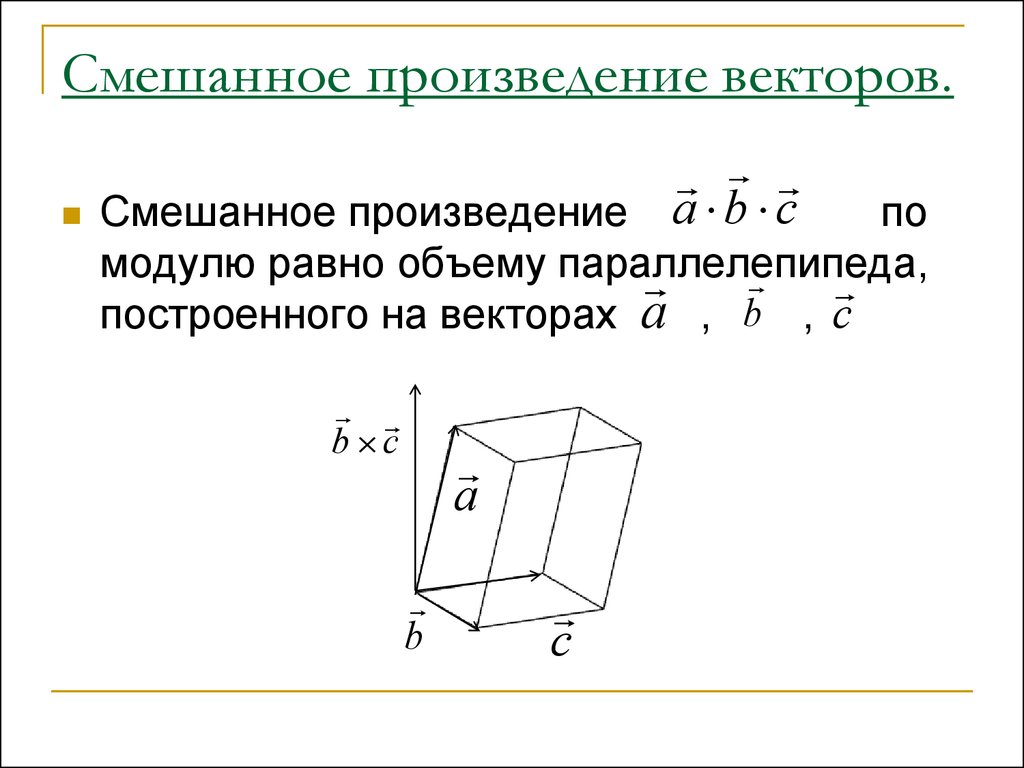
55. Смешанное произведение векторов.

Смешанное произведение a b c
по
модулю равно объему параллелепипеда,
построенного на векторах a , b , c
b c
a
b
c

56. Свойства смешанного произведения векторов.

1)Смешанное произведение равно нулю, если:
а) хоть один из векторов равен нулю;
б) два из векторов коллинеарны;
в) векторы компланарны.
2) ( a b ) c a (b c )
(a , b , c ) (b , c , a ) (c , a , b ) (b , a , c ) (c , b , a ) (a , c , b )
3)
( a1 a 2 , b , c ) (a1 , b , c ) (a 2 , b , c )
4)
5) Объем треугольной
пирамиды, образованной
векторами
a , b, c
равен
1
a, b , c
6

57. Свойства смешанного произведения векторов:

6) Если a ( x1, y1, z1) , b ( x2 , y2 , z 2 ), c ( x3 , y3 , z3 )
то
x1
(a , b , c ) x 2
y1
y2
z1
z2
x3
y3
z3

58. 5. Аналитическая геометрия на плоскости и в пространстве

Математический форум Math Help Planet
Эл. адрес http://mathhelpplanet.com

59. Произведение вектора на число

60. Произведение вектора на число

При движении с постоянной скоростью v
перемещение s за время t выражается
формулой: s v t
Импульс тела определяется как
произведение массы на скорость: p v m
Второй закон Ньютона F a m , где F - сумма
векторов всех сил, приложенных к телу
Электрическое поле характеризуется вектором
напряжения, который задан в каждой точке поля,
если в данную точку помещен заряд q, то сила
действующая на этот заряд со
стороны
электрического поля равна: F E q