Похожие презентации:
Метод интервалов в тригонометрических неравенствах
1.
Методинтервалов в
тригонометрических
неравенствах
2.
Решение тригонометрических неравенств методом интерваловАлгоритм:
1)С помощью тригонометрических формул разложить на множители.
2)Найти точки разрыва и нули функции, поставить их на окружность.
3)Взять любую точку x0 (но не найденную ранее) и выяснить знак
произведения. Если произведение положительно, то поставить «+» за
единичной окружностью на луче, соответствующему углу. Иначе
поставить знак «-» внутри окружности.
4)Если точка встречается четное число раз, назовем ее точкой четной
кратности, если нечетное число раз – точкой нечетной кратности. Провести
дуги следующим образом: начать с точки x0 , если следующая точка
нечетной кратности, то дуга пересекает окружность в этой точке, если же
точка четной кратности, то не пересекает.
5)Дуги за окружностью – положительные промежутки; внутри окружности
– отрицательные промежутки.
3.
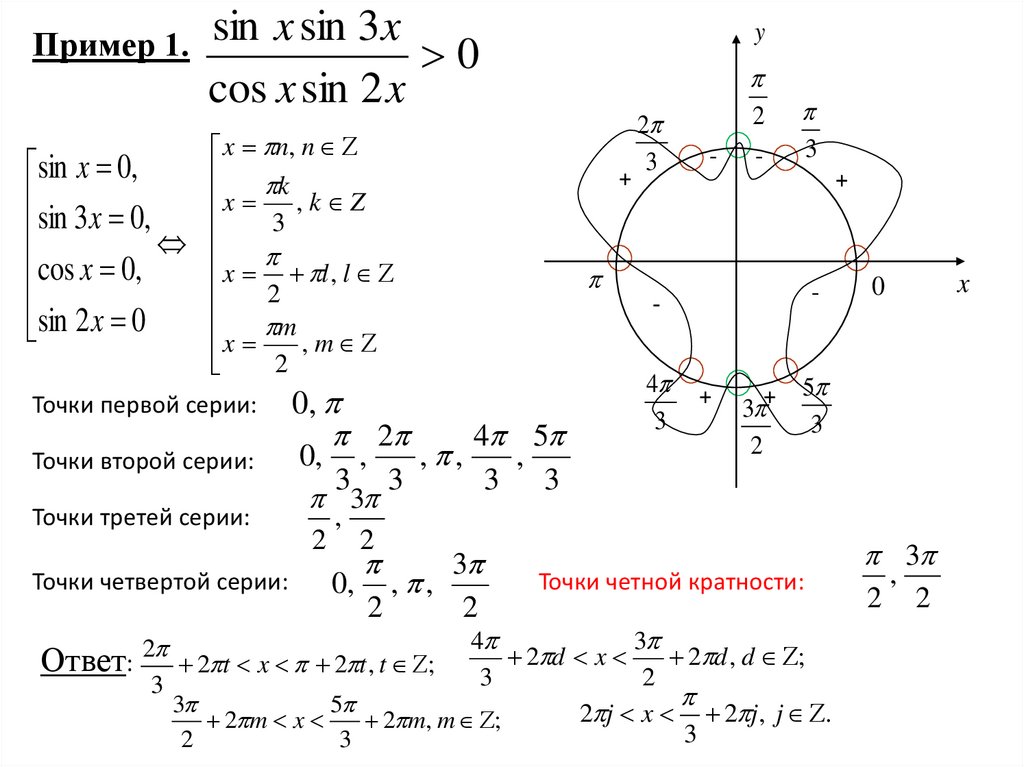
Пример 1. sin x sin 3 x 0y
cos x sin 2 x
sin x 0,
sin 3x 0,
cos x 0,
sin 2 x 0
x n, n
x k , k Z
3
x l , l
2
m
x
, m
2
Точки первой серии:
Точки второй серии:
Точки третей серии:
Точки четвертой серии:
0,
2
+
4 5
0, ,
, ,
,
3 3
3 3
3
2
,
2
3
2
-
-
3
+
-
-
4
3
+
3 +
2
5
3
2
3
0, , ,
2
2
0
Точки четной кратности:
4
3
2
2
d
x
2 d , d ;
Ответ: 2 t x 2 t , t ; 3
2
3
3
5
2
j
x
2 j , j .
2 m x
2 m, m ;
3
2
3
3
,
2 2
x
4.
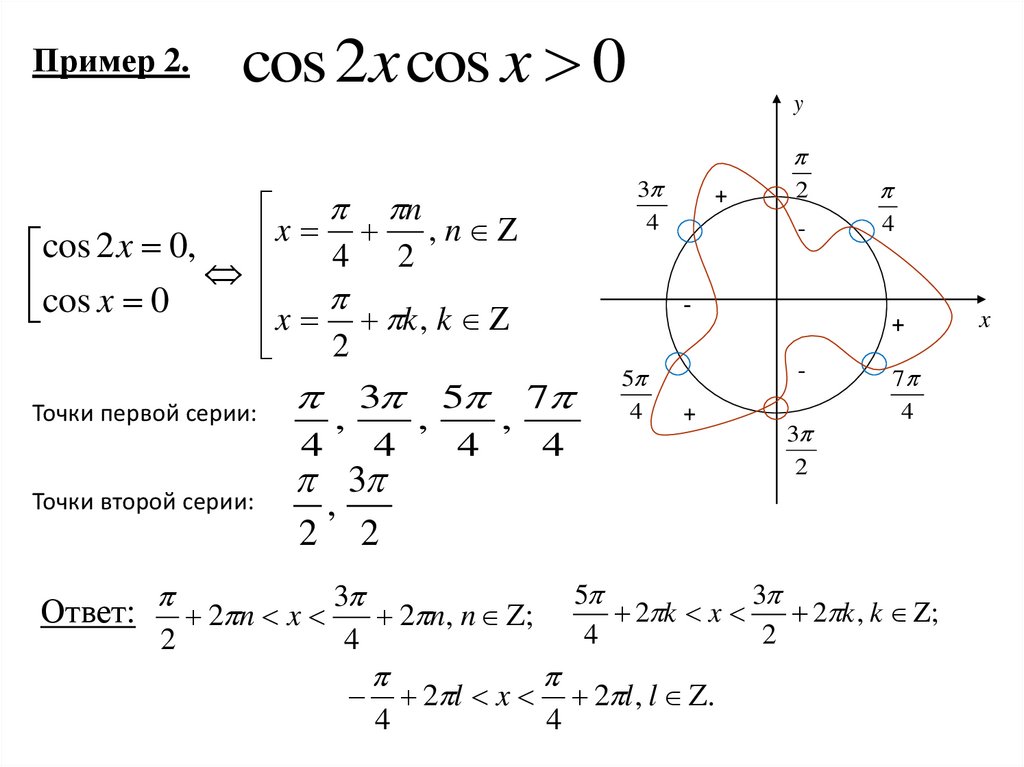
Пример 2.cos 2x cos x 0
y
3
4
n
x 4 2 , n
cos 2 x 0,
cos x 0
x k , k
2
Точки первой серии:
Точки второй серии:
3 5 7
,
,
,
4 4
4
4
5
4
-
4
+
-
+
3
,
2
-
2
3
2
7
4
2
Ответ: 2 n x 3 2 n, n ;
2
+
4
4
2 l x
5
3
2 k x
2 k , k ;
4
2
4
2 l , l .
x
5.
tgx ctgx 0Пример 3.
1 tg 2 x 1
2
tgx ctgx tgx
tgx
tgx
sin 2 x
1) Нули числителя :f ( x) 0,
2) Нули знаменателя
y
3)
2
+
2
0
sin 2 x
- нулей числителя нет
Точки разрыва :
n
2
, n
-
+
-
3
2
0
x
Итак,
f ( x) 0
n
2
при
x n, n
6.
Домашнее задание2 sin x 1 (двумя способами)
2
2 sin x 3
sin x
sin x sin 3 x
0
cos x sin 2 x




 Математика
Математика








