Похожие презентации:
Алгоритмическая торговля. Научный подход
1.
Алгоритмическая торговляНаучный подход
Ведущий курса:
Александр Горчаков
1
2.
Введение2
3. Случайность и детерминированность – Pro et Contra
Будущее• детерминировано, т. е. все будущие
события однозначно
предопределены прошлым.
ИЛИ
• случайно, т. е. будущие события не
предопределены прошлым, а
прошлое лишь может влиять на
шансы (вероятности) их появления.
3
4. Вероятность
• 0≤Р(ω)≤1;• Если одновременное появление событий
ω1 и ω2 невозможно, то
Р(ω1 И ω2 )=0
• Если Р(ω1 И ω2)=0, то
Р(ω1 ИЛИ ω2) =Р(ω1)+Р(ω2);
• Если ω1 включает в себя ω2, то
Р(ω2) ≤Р(ω1).
• Вероятность хотя бы одного из всех
возможных событий (достоверное
событие) равна 1
4
5. Что такое торговый алгоритм (торговая система)?
Начнем с самого общего определения торгового алгоритма.Определение 1. Торговый алгоритм – это алгоритм,
преобразующий прошлую входящую информацию в
текущее состояние счета.
Т. е. в обывательском смысле – это что-то типа машинки,
печатающей деньги
5
6. От чего зависит эквити счета?
nC (i ) V (i) D
i 1
t
t
t
n
(i) V (i),
i 1
t 1
t
где t 1 (i ) Сt 1 (i ) Сt (i )
6
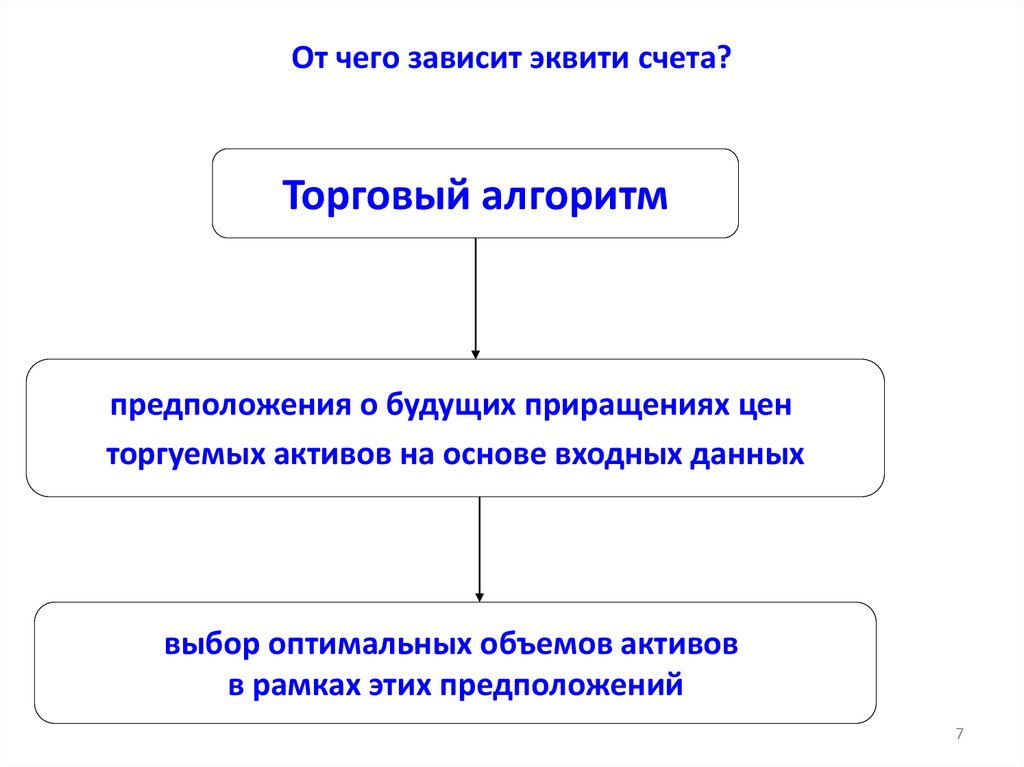
7. От чего зависит эквити счета?
Торговый алгоритмпредположения о будущих приращениях цен
торгуемых активов на основе входных данных
выбор оптимальных объемов активов
в рамках этих предположений
7
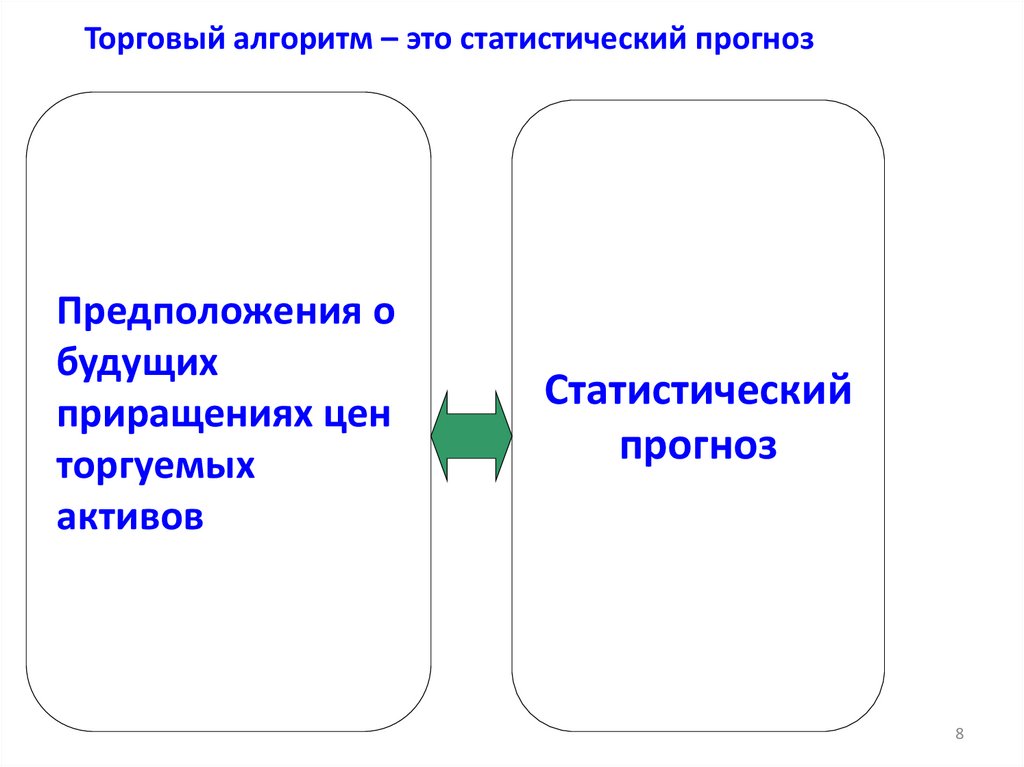
8. Торговый алгоритм – это статистический прогноз
Предположения обудущих
приращениях цен
торгуемых
активов
Статистический
прогноз
8
9. Что можно подавать на вход торгового алгоритма?
Входные данные торговогоалгоритма должны
удовлетворять трем условиям:
- регулярность;
- достоверность;
- формализуемость.
9
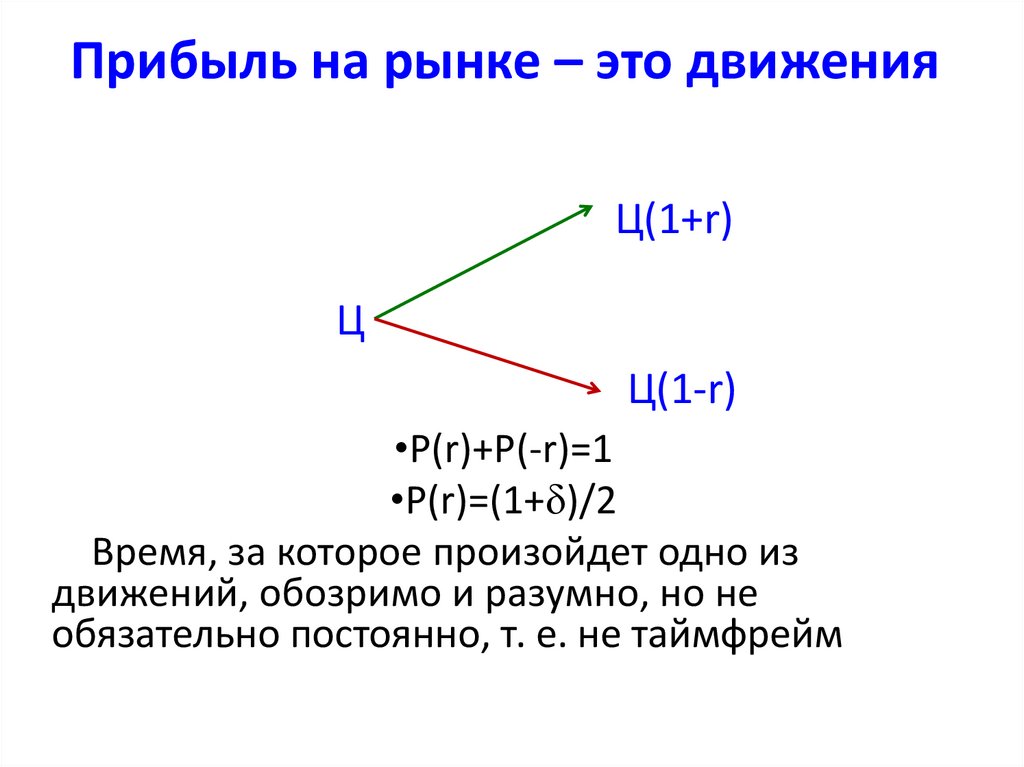
10. Прибыль на рынке – это движения
Ц(1+r)Ц
Ц(1-r)
•P(r)+P(-r)=1
•P(r)=(1+ )/2
Время, за которое произойдет одно из
движений, обозримо и разумно, но не
обязательно постоянно, т. е. не таймфрейм
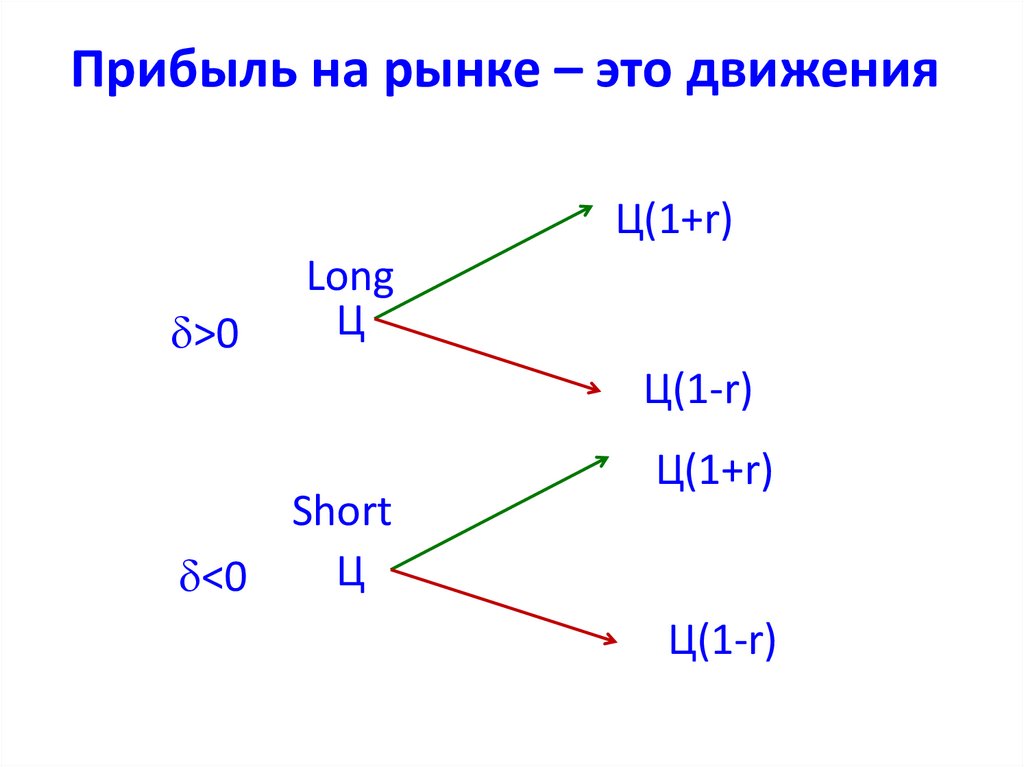
11. Прибыль на рынке – это движения
Ц(1+r)>0
Long
Ц
Ц(1-r)
Short
Ц
<0
Ц(1+r)
Ц(1-r)
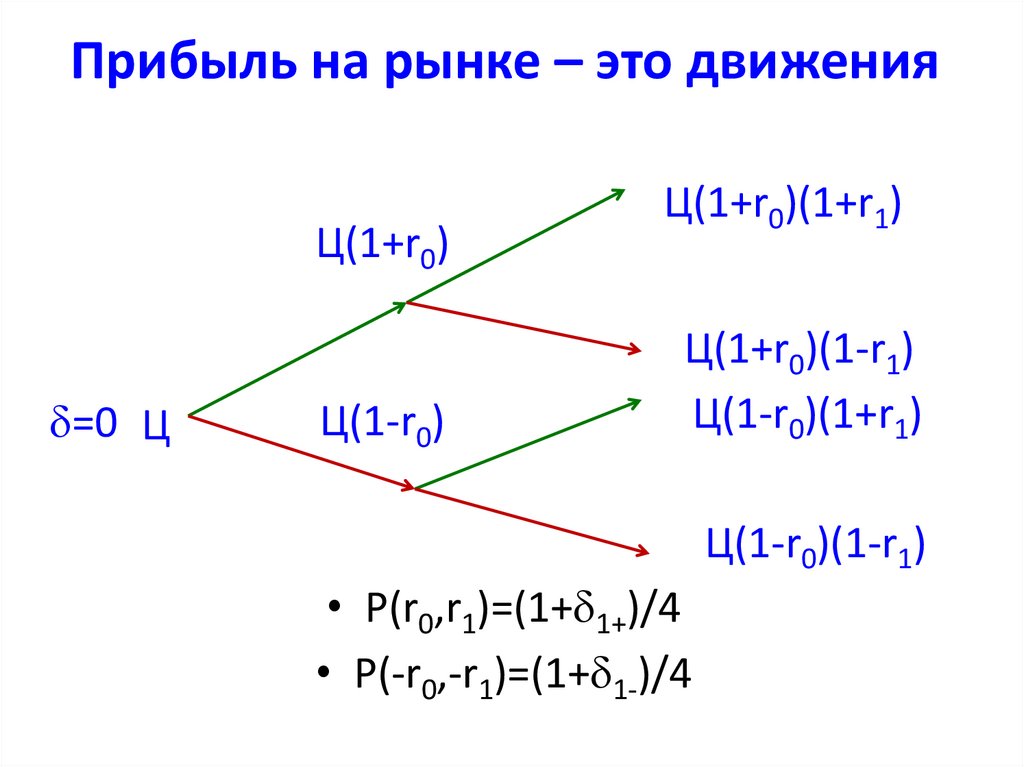
12. Прибыль на рынке – это движения
Ц(1+r0)=0 Ц
Ц(1-r0)
Ц(1+r0)(1+r1)
Ц(1+r0)(1-r1)
Ц(1-r0)(1+r1)
Ц(1-r0)(1-r1)
• P(r0,r1)=(1+ 1+)/4
• P(-r0,-r1)=(1+ 1-)/4
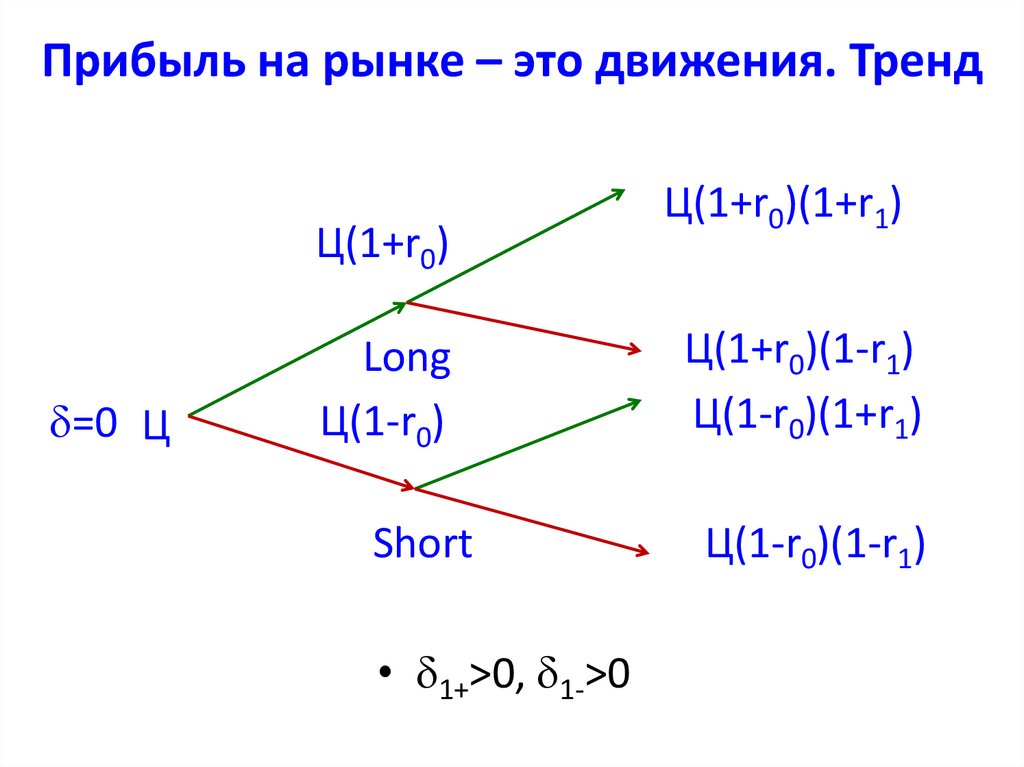
13. Прибыль на рынке – это движения. Тренд
Ц(1+r0)=0 Ц
Ц(1+r0)(1+r1)
Long
Ц(1-r0)
Ц(1+r0)(1-r1)
Ц(1-r0)(1+r1)
Short
Ц(1-r0)(1-r1)
• 1+>0, 1->0
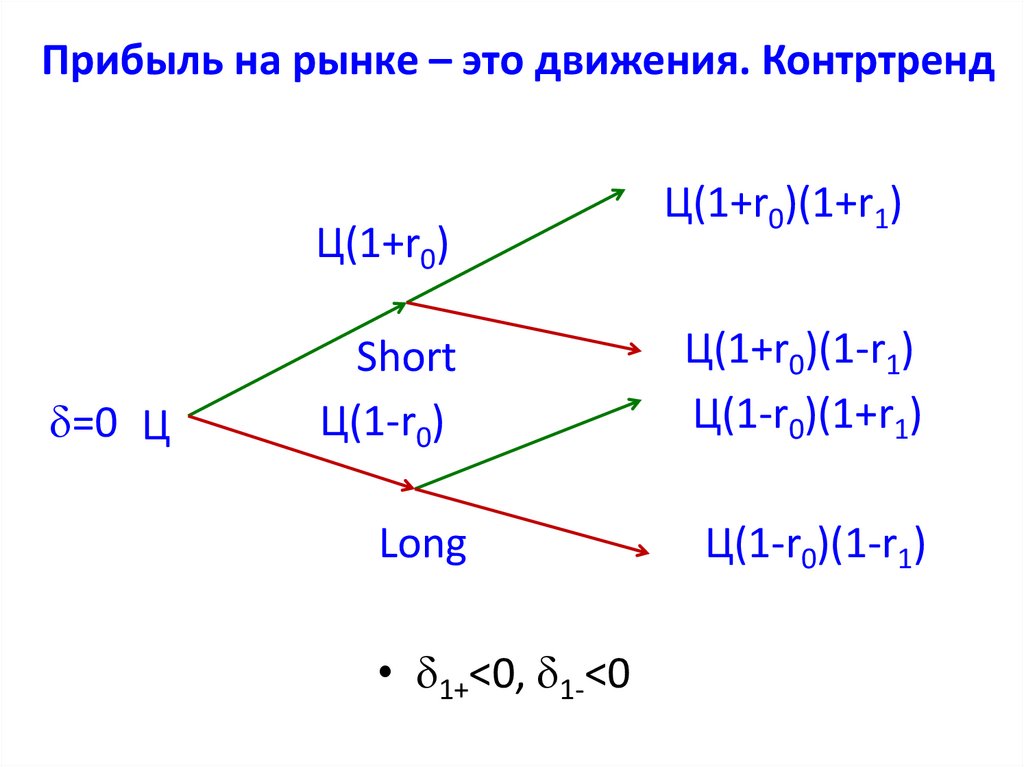
14. Прибыль на рынке – это движения. Контртренд
Ц(1+r0)=0 Ц
Ц(1+r0)(1+r1)
Short
Ц(1-r0)
Ц(1+r0)(1-r1)
Ц(1-r0)(1+r1)
Long
Ц(1-r0)(1-r1)
• 1+<0, 1-<0
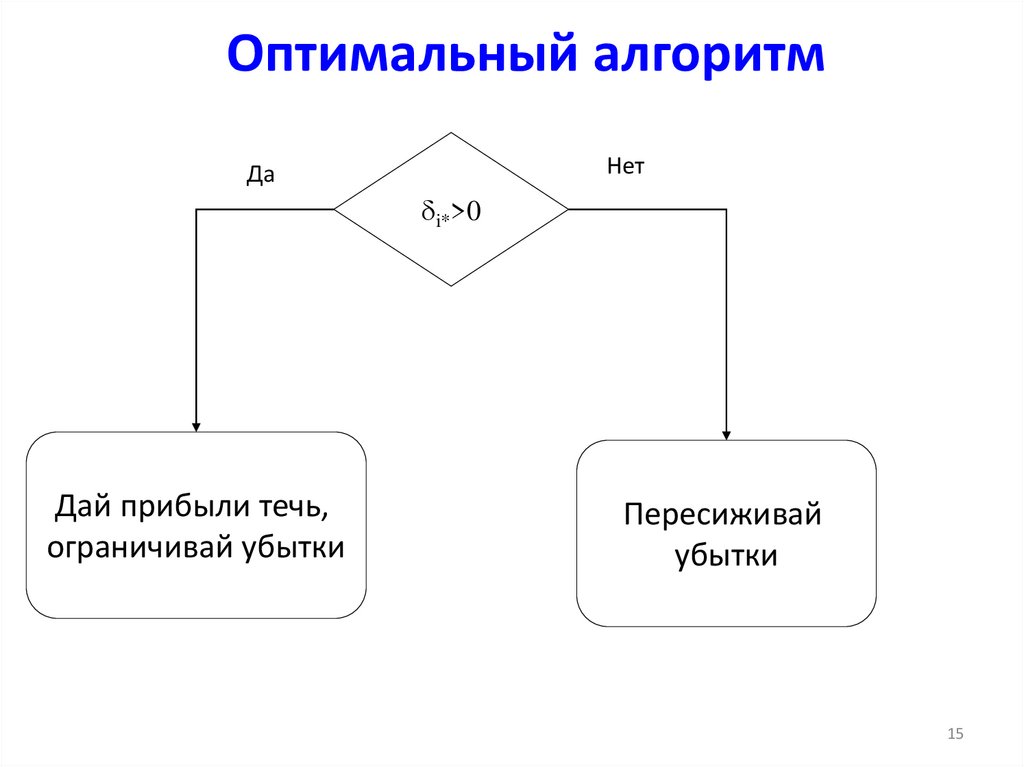
15. Оптимальный алгоритм
НетДа
i*>0
Дай прибыли течь,
ограничивай убытки
Пересиживай
убытки
15
16. Оптимальный алгоритм
Отметим, что оптимальный алгоритм вобоих случаях представляет собой игру в
«бросание монетки» с вероятностью
выигрыша (1+|δi*|)/2 . Это позволяет
строить оптимальные схемы усреднения
позиции для ограничения просадки счета.
Заметим, что если мы не угадали со
знаком δi*, то опять получаем игру в
«бросание монетки», но с вероятностью
выигрыша (1-|δi*|)/2, т. е. заведомо
проигрышную.
16
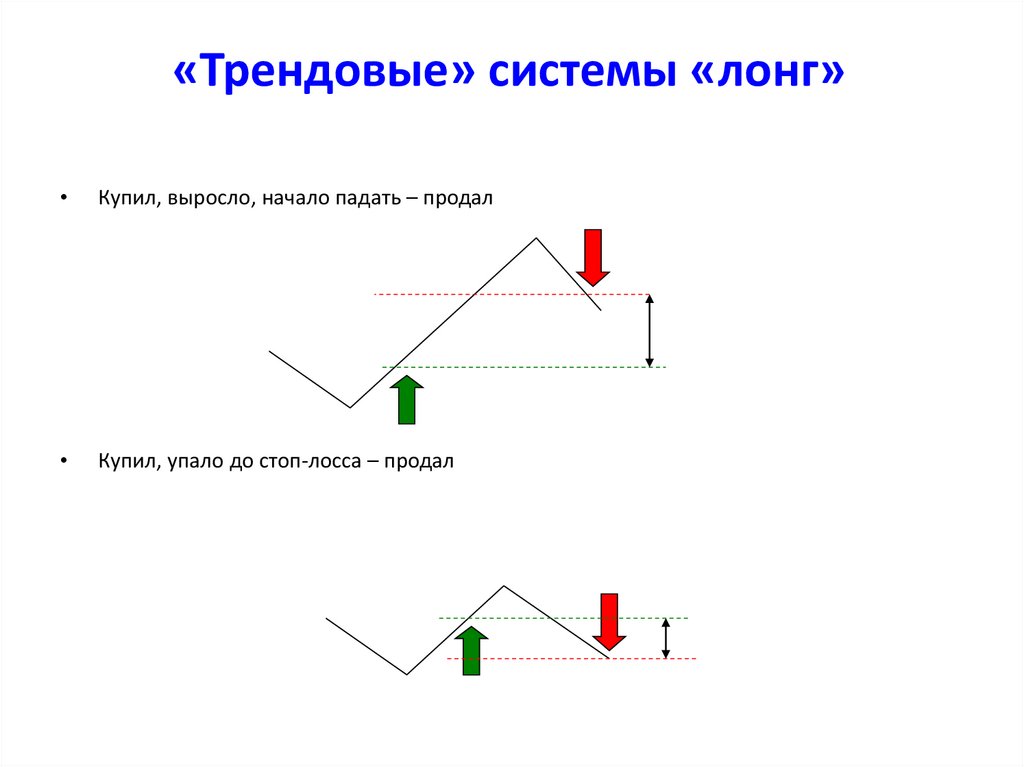
17. «Трендовые» системы «лонг»
Купил, выросло, начало падать – продал
Купил, упало до стоп-лосса – продал
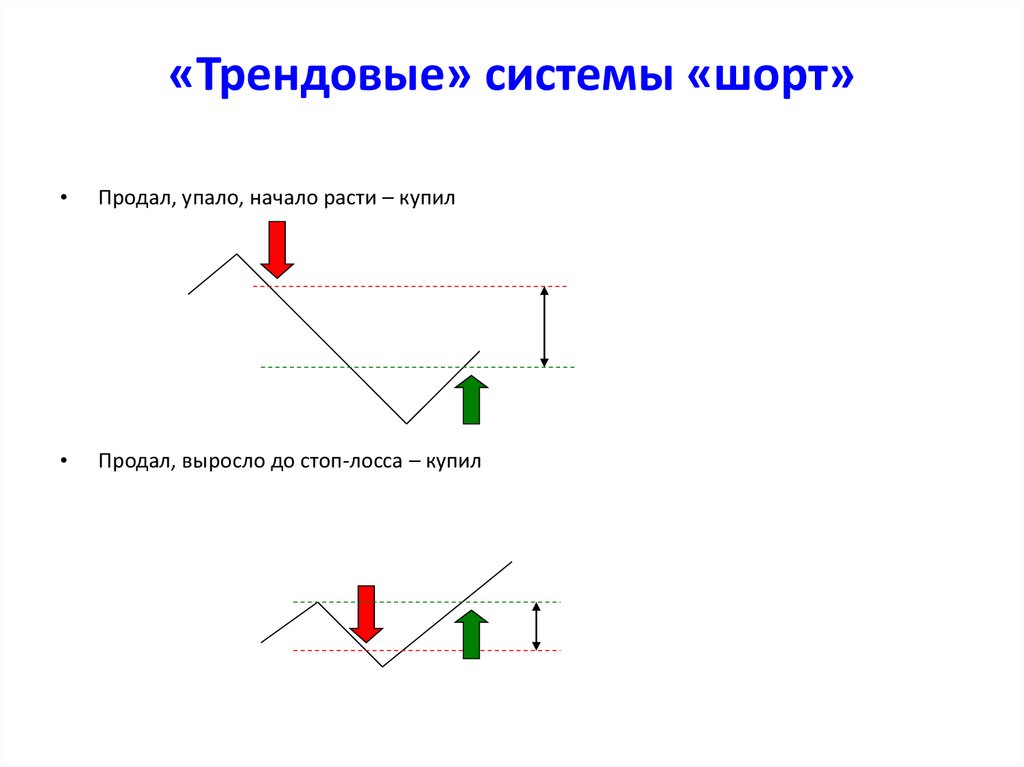
18. «Трендовые» системы «шорт»
Продал, упало, начало расти – купил
Продал, выросло до стоп-лосса – купил
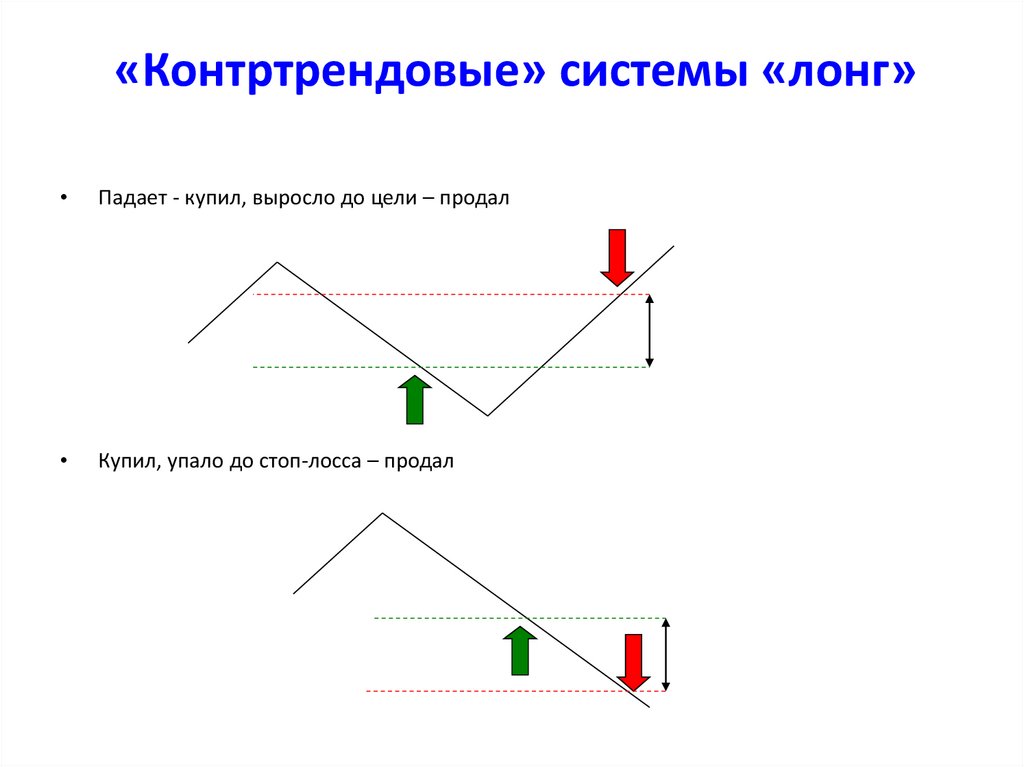
19. «Контртрендовые» системы «лонг»
Падает - купил, выросло до цели – продал
Купил, упало до стоп-лосса – продал
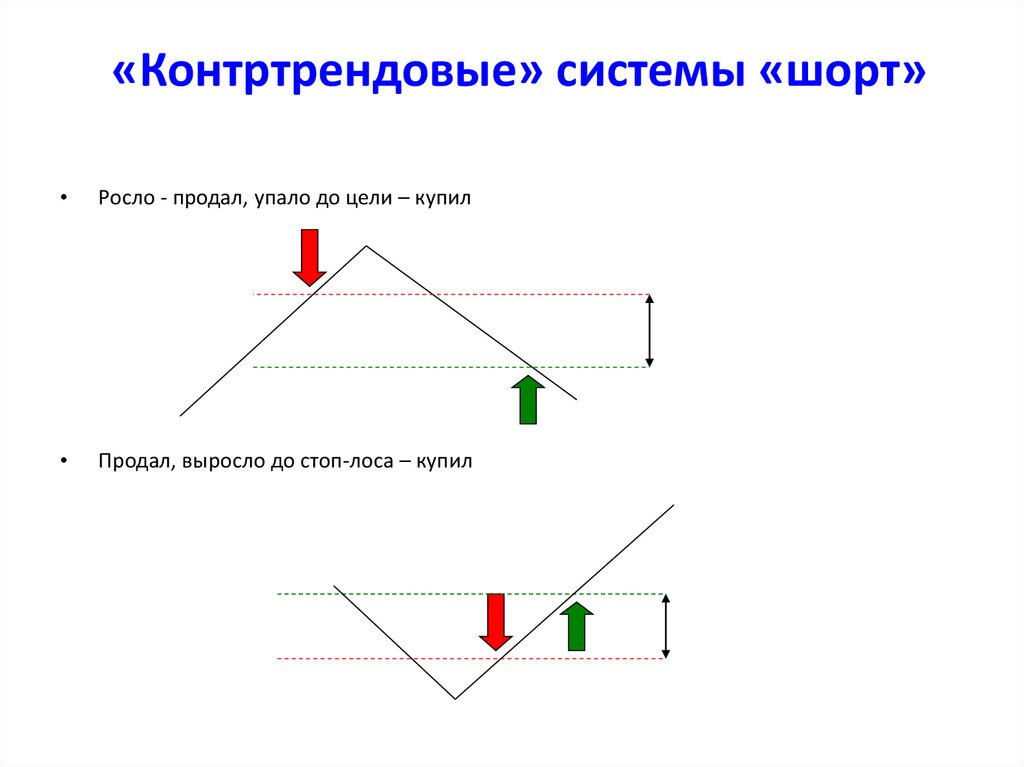
20. «Контртрендовые» системы «шорт»
Росло - продал, упало до цели – купил
Продал, выросло до стоп-лоса – купил
21.
Основные понятиятеории вероятностей и
математической статистики
21
22. Случайная величина
X: Ω → RФункция распределения:
F(x)=P(X≤x),
•F(x) – монотонно возрастает по х,
•P(X=х)= F(x)- F(x-), F(x-)=P(X<x),
•F(+ )=1, F(- )=0
Дискретная случайная величина
Существуют такие значения х1, х2, ….,
что
Р(Х=хi)=р(хi) и ∑р(xi)=1
22
23. Случайная величина
Непрерывное распределениеF(x)- непрерывна, т. е. F(x)= F(x-)
Абсолютно непрерывное распределение
Существует такая функция f(x)
x
F ( x ) f ( y ) dy
f(x) – плотность распределения.
23
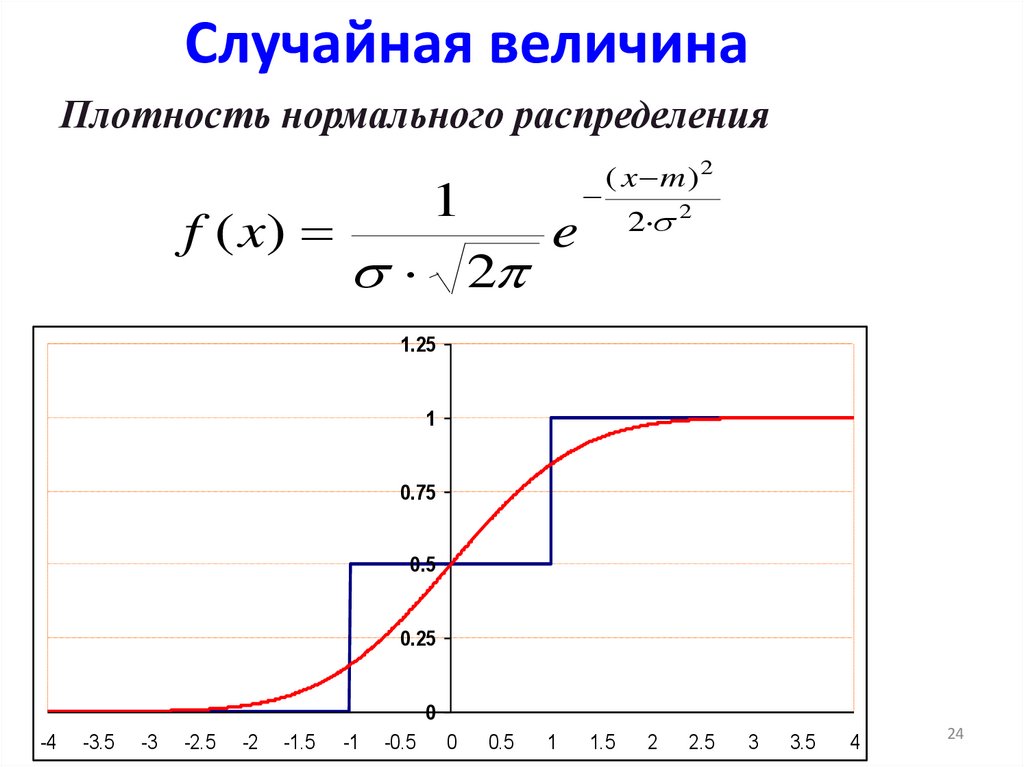
24. Случайная величина
Плотность нормального распределенияf ( x)
1
2
( x m)2
e
2 2
1.25
1
0.75
0.5
0.25
0
-4
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
3
3.5
4
24
25. Случайная величина
Математическое ожидание (среднее)функции от случайной величины
g ( xi ) p ( xi )
i
Eg ( X )
g ( x) f ( x) dx
Математическое ожидание EX
Дисперсия DX=E(X-EX)2
Стандартное отклонение ( X ) DX
25
26. Случайная величина
Квантиль (α-квантиль)F ( x)
x
F ( x )
Для непрерывного распределения
α=F(xα)
n% перцентиль - α-квантиль для
n%
100%
n%VAR- n% перцентиль (как правило,
отрицательный).
26
27. Случайная величина
n%CVARE(X∙I(X≤n%VAR))
где
1, если X a;
I ( X a)
0, если X a;
27
28. Многомерные случайные величины
X : Ω → RmФункция распределения
F(x1,…,xm)=P(X1≤x1,…,Xm≤xm)
Дискретные многомерные случайные
величины
Существует дискретное множество mмерных векторов x=(x1,…,xm) таких, что
p(x1,…,xm)= P(X1=x1,…,Xm=xm)
∑ p(x1,…,xm)= 1
28
29. Многомерные случайные величины
Абсолютно непрерывные многомерныеслучайные величины
Существует функция f(x1,…,xm) такая,
что
x1
xm
F ( x1 ,..., xm ) ... f ( y1 ,..., ym )dy1 ... dym
29
30. Многомерные случайные величины
Многомерное нормальное распределение– это многомерное распределение, у
которого произвольная линейная
комбинация
n
а X
i 1
i
i
имеет одномерное нормальное
распределение или является константой.
30
31. Многомерные случайные величины
Независимые случайные величиныДля любых (x1,…,xm):
для дискретной случайной величины
p(x1,…,xm)=p1(x1)∙…∙pm(xm)
Для абсолютно непрерывной случайной
величины
f(x1,…,xm)=f1(x1)∙…∙fm(xm)
31
32. Многомерные случайные величины
g(Х1,…,Хm) – некоторая одномернаяфункция. Математическое ожидание
(среднее) g равно
g ( x1 ,..., xm ) p( x1 ,..., xm )
Eg ( X 1 ,..., X m )
... g ( x1 ,..., xm ) f ( x1 ,..., xm )dx1 ... dxm
Ковариация двух одномерных случайных
величин
COV(X,Y)=E(X∙Y)-EX∙EY
32
33. Корреляция
Корреляция двух одномерных случайныхвеличин
COV ( X , Y )
CORR ( X , Y )
( X ) (Y )
–|CORR(X,Y)|=1, тогда и только тогда,
когда Х=аY+b, причем
sign(a)=sign(CORR(X,Y))
–если |CORR(X,Y)|≠0, то Х и Y –
зависимы
–если Х и Y – независимы, то
CORR(X,Y)=0
33
34. Стохастическое доминирование
I родаFX(x)≤FY(x) или Y (≤1) X
II рода
E(X∙I(X≤x))≤E(Y∙I(Y≤x)) или Y (≤2) X
Если, чем больше значение
переменной х, тем лучше, то Х
«лучше» Y.
34
35. Условное распределение
X и Y -дискретные многомерные случайныевеличины
Р(Х/(y1,…,yn)) - дискретное распределение с
вероятностями
p( x1 ,..., xm , y1 ,..., y n )
p( y1 ,..., y n )
X и Y - абсолютно непрерывные многомерные
случайные величины
Р(Х/(y1,…,yn)) - абсолютно непрерывное
распределение с плотностью
f ( x1 ,..., xm , y1 ,..., y n )
f ( y1 ,..., y n )
35
36. Условное распределение
Условное распределение Р(Х/(y1,…,yn)) – этомаксимум того, что мы можем знать о
реализации случайной величины Х при
условии, что мы наблюдаем реализацию
(y1,…,yn) случайной величины Y.
Определение. Задача статистического
прогноза - это задача оценки условного
распределения и(или) его параметров.
36
37. Условные среднее и дисперсия
Х - одномерная случайная величина.Среднее случайной величины с
распределением Р(X/(y1,…,yn)), называется
условным средним (обозначается
E(X/(y1,…,yn))), а дисперсия - условной
дисперсией (D(X/(y1,…,yn))).
Условные среднее и дисперсия являются
одномерными случайными величинами,
так как являются преобразованиями
многомерной случайной величины Y .
37
38. Условные среднее и дисперсия
Cреднеквадратичным отклонениемпрогноза g(y1,…,yn) называется величина
Δg=E(X-g(Y))2 ,
где усреднение ведется по
распределению многомерной случайной
величины Y.
Минимум Δg достигается при
g(y1,…,yn)= E(X/(y1,…,yn))
и равен ED(X/Y).
38
39. Регрессия
Детерминированность – это частныйслучай случайности при Δg=0.
E(X/(y1,…,yn)), как функция от (y1,…,yn),
называется функцией регрессии.
Таким образом, оптимальный в
среднеквадратичном статистический
прогноз является ни чем иным, как
функцией от известных (при временном
ряде -прошлых) значений наблюдаемых
случайных величин.
39
40. Регрессия
Если (X,Y) имеет многомерноенормальное распределение, то
E(X/(y1,…,yn)) равна
n
a y
i 1
i
i
где аi не зависят от (y1,…,yn).
Т. е. в этом случае оптимальным в
среднеквадратичном прогнозом
является линейная регрессия.
40
41. Последовательности случайных величин
Х1, Х2,…,Стационарность в широком смысле
ЕХi=a, EXi∙Xj=γ(|j-i|)
Стационарность в узком смысле
Для любых i1<….<im и t=1,2,….
FX i ,..., X im ( x1 ,..., xm ) FX i t ,..., X im t ( x1 ,..., xm )
1
1
41
42. Последовательности случайных величин
Последовательность независимыхслучайных величин: Для любых i1<…<im
X i1 ,..., X im
независимы
Гауссовская последовательность – это
стационарная в узком смысле
последовательность: Для любых i1<…<im
FX i ,..., X im ( x1 ,..., xm )
1
многомерное нормальное распределение
42
43. Случайное блуждание
Х1, Х2,…, - случайное блуждание, еслиX2-X1, X3-X2,…, - стационарная в узком
смысле последовательность независимых
случайных величин.
Х1, Х2,…, - геометрическое случайное
блуждание, если
LnX1, LnX2,…, - случайное блуждание.
Отметим, что случайное блуждание в
общем случае не является стационарным
процессом.
43
44. Автокорреляционная функции
Автокорреляционная функция (АКФ) длястационарных в широком смысле
последовательностей (!) с конечной
дисперсией равна
( n) a
( n)
2
(0) a
2
Для последовательности независимых
случайных величин АКФ - нулевая, вне
зависимости от выполнения условия
стационарности.
44
45. Спектральная функция
(0) as( )
[1 2 (i) cos( i)], 0
i 0
2
Спектральная функция – это
преобразование Фурье АКФ.
Спектральная функция – непрерывная
функция, широкие пики в ней
соответствуют нерегулярным циклам,
узкие – более регулярным. Для нулевой
АКФ спектральная функция –
константа.
45
46. Показатель Херста
mX
m
i 1
i
m
m
Rn max ( m n ) min ( m n )
m n
m n
n
n
Rn
c
H n
n
H – коэффициент (показатель) Херста.
Если Х1, Х2,…, -последовательность
независимых случайных величин с
конечной дисперсией, то H=½.
46
47. Показатель Херста
Случаи H≠½.1.Пусть Х1, Х2,…, - последовательности
независимых случайных величин с распределением
Коши (дисперсия бесконечна). Тогда H=1.
2.Пусть Х1, Х2,…, - гауссовская последовательность
с нулевым средним
γ(k)=½((k-1)2h-2k2h+(k+1)2h)
Тогда H=h, а последовательность ∑1, ∑2,…,
называют фрактальным броуновским
движением, которое представляет собой
обобщение стандартного броуновского движения
(винеровского процесса), получающегося при H=½.
47
48. Показатель Херста
Для стационарных последовательностей(!) отличие коэффициента Херста от ½
может означать либо «сверхтяжелые
хвосты», либо сильную зависимость
(убывающую с «расстоянием» по
степенной функции). Для случая
экспоненциального убывания зависимости
с «расстоянием» или конечной
зависимости, коэффициент Херста равен
½, хотя для близлежащих значений этих
последовательностей зависимость может
быть очень сильной.
48
49. Выборка
Выборка – это реализация конечного отрезканекоторой последовательности случайных
величин.
Статистика – это некоторая функция от
выборки.
Наиболее известные статистики
Выборочное среднее
1 n
xi
n i 1
Выборочная дисперсия
1 n
1 n
2
(
x
(
x
)
)
i
i
n 1 i 1
n i 1
49
50. Достаточные статистики
Если функция распределения многомернойслучайной величины, реализацией которой
является выборка имеет вид
F(g1(х1,…,хn),…, gm(х1,…,хn)), m<n
то статистики g1,…, gm называются
достаточными статистиками.
Отметим, что преобразование выборки в
последовательность достаточных статистик не
уменьшает информации об исходном
распределении, содержащейся в выборке. Для
независимых одинаково распределенных
нормальных случайных величин достаточными
статистиками являются выборочное среднее и
дисперсия.
50
51. Задачи статистики
Различение гипотезH0: F(x1,…,xn) из множества
распределений F0 ;
H1: F(x1,…,xn) из множества
распределений F1 ;
F0 и F1 не пересекаются.
Строим такую статистику g и
разбиение R на два непересекающихся
подмножества R0 и R1, что если gЄ R0 ,
то принимаем гипотезу H0
51
52. Задачи статистики
Оценивание параметровF(x1,…,xn) = G(x1,…,xn, a) , где а –
неизвестен.
Задача построить такую статистику
g, которая была бы «близка» к значению
a.
Несмещенной называется
статистика, для которой
Eg=a
52
53. Параметрическая статистика
Параметрической называют такие задачистатистики, в которых функции
распределения задаются в виде четкой
формулы за исключением неизвестных
параметров распределения.
Соответственно, отказ от условия явного
вида функции распределения приводит к
непараметрической статистике. В частности,
задача проверки стационарности
произвольной последовательности
случайных величин – задача
непараметрической статистики.
53








































 Математика
Математика








