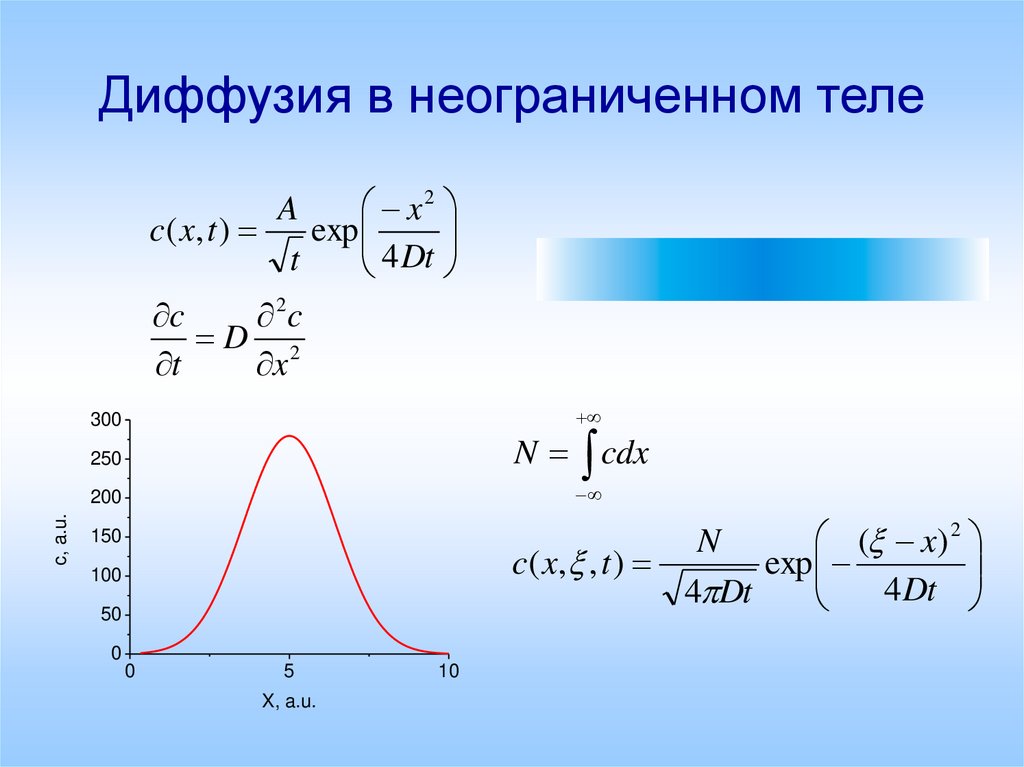
Диффузия в неограниченном теле

1. Диффузия в неограниченном теле

x2
A
c ( x, t )
exp
t
4 Dt
c
2c
D 2
t
x
300
N cdx
250
c, a.u.
200
( x) 2
N
c ( x, , t )
exp
4 Dt
4 Dt
150
100
50
0
0
5
X, a.u.
10

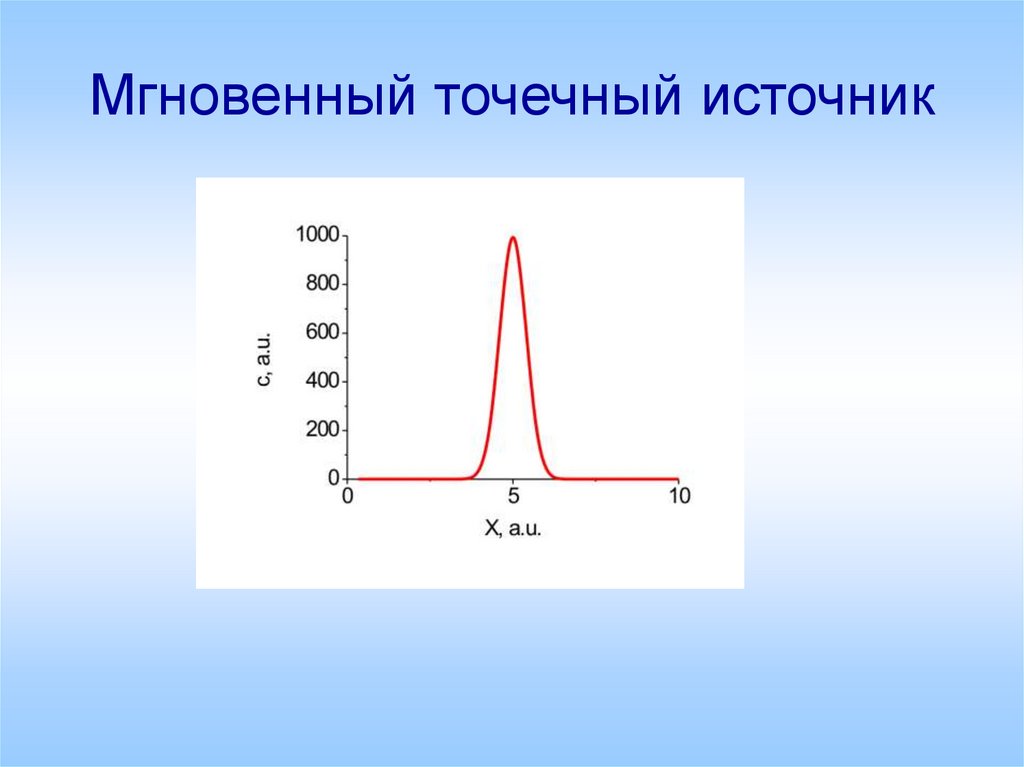
2. Мгновенный точечный источник

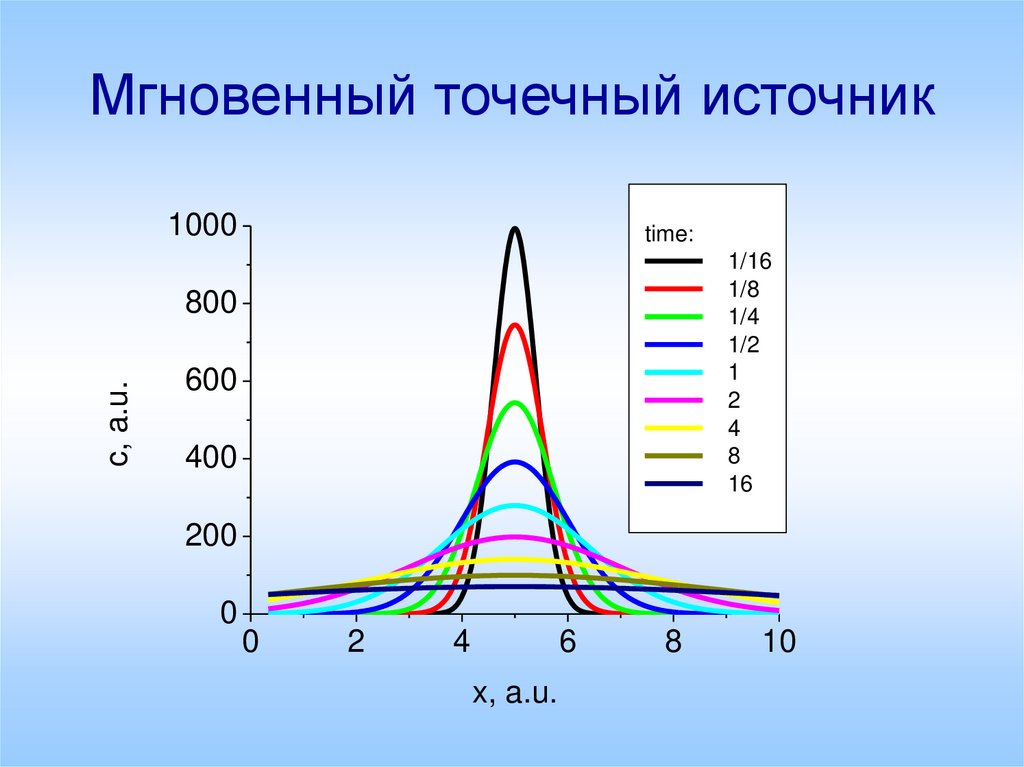
3. Мгновенный точечный источник

1000
time:
1/16
1/8
1/4
1/2
1
2
4
8
16
c, a.u.
800
600
400
200
0
0
2
4
6
x, a.u.
8
10

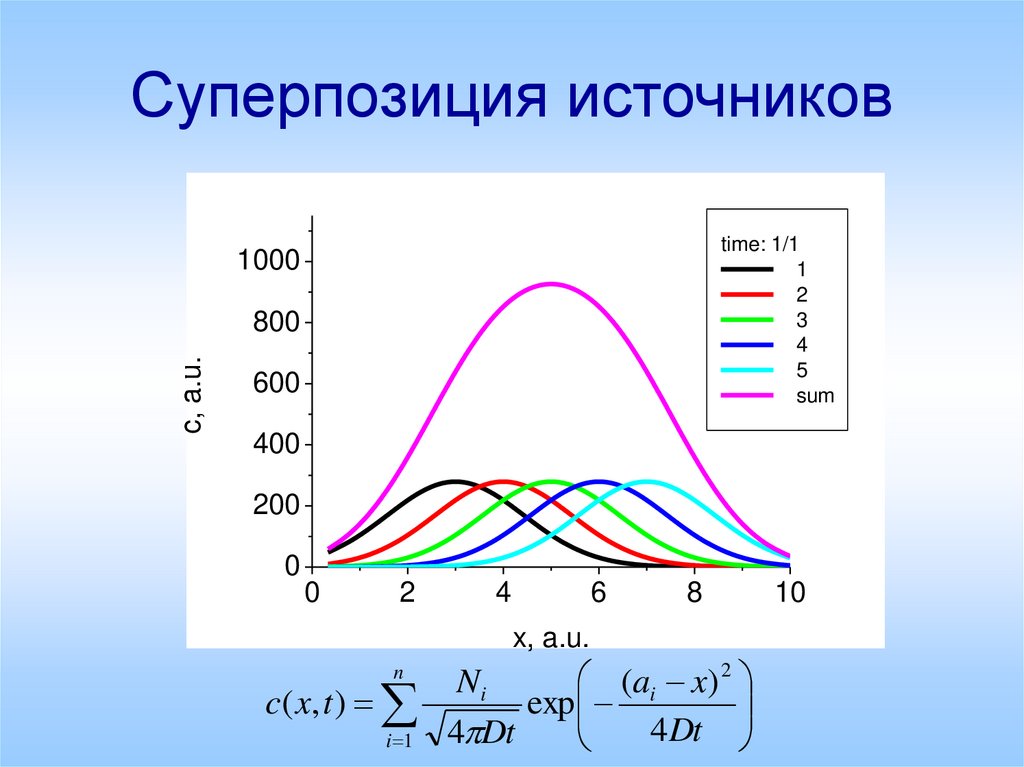
4. Суперпозиция источников

time: 1/2
1/16
1/8
1/4
1/1
1
2
3
4
5
sum
1000
c, a.u.
800
600
400
200
0
0
2
4
6
8
x, a.u.
n
c( x, t )
i 1
(ai x) 2
Ni
exp
4 Dt
4 Dt
10

5. Интеграл по источникам

( x) 2
1
d
c( x, t )
f ( ) exp
4 Dt
4 Dt
• фундаментальное решение уравнения
диффузии:
( x) 2
1
G( x, , t )
exp
4 Dt
4 Dt

6. Интеграл по источникам, строгий вывод

c
2c
D 2
t
x
x
c( x, t ) t 0 c( x,0) f ( x)
c ( x, t ) ?
• Метод разделения переменных:
c( x, t ) X ( x)T (t )
1 1 dT 1 d 2 X
2
D T dt X dx 2
T (t ) A exp 2 Dt
X ( x) B exp i x
c( x, t ) C exp( 2 Dt ) exp( i x)
c( x, t ) C ( ) exp( 2 Dt ) exp( i x)d
c( x,0) f ( x) C ( ) exp( i x)d
C ( )
1
f ( ) exp( i )d
2

7. Интеграл по источникам, строгий вывод

1
2
c( x, t ) exp( Dt )
f ( ) exp( i )d exp( i x)d
2
1
2
c ( x, t )
f ( ) exp Dt i ( x) d d
2
2
2
d ( Dt )
1
( x)
i
(
x
)
d
Dt
c ( x, t )
f
(
)
exp
exp
2
4
Dt
4
Dt
Dt
( x) 2
1
d
c ( x, t )
f ( ) exp
2
4
Dt
Dt
( x) 2
1
d
c( x, t )
f ( ) exp
4 Dt
4 Dt

8. Начальные условия

• замена переменной:
z
x
x z 4 Dt
4 Dt
d 4 Dt dz
• тогда:
c ( x, t )
1
c ( x ,0 )
1
2
f
(
x
z
4
Dt
)
exp
z
dz
2
f
(
x
)
exp
z
dz f ( x)

9. Сохранение количества частиц

• если в момент времени t = 0
f ( )d N
0
• то для t > 0
1
( x) 2
d dx
N (t ) c( x, t )dx
f ( ) exp
4 Dt
4 Dt
1
( x) 2
dx d N 0
N (t ) f ( )
exp
4 Dt
4 Dt

10. Симметричное начальное распределение

• если:
• то:
c( ,0) c( ,0)
( x) 2
1
d
c ( x, t )
c( ,0) exp
4 Dt
4 Dt
( x) 2
1
d
c( ,0) exp
4 Dt
4 Dt
( z x) 2
1
dz c( x, t )
c( z ,0) exp
4 Dt
4 Dt
c ( x, t ) c ( x, t )

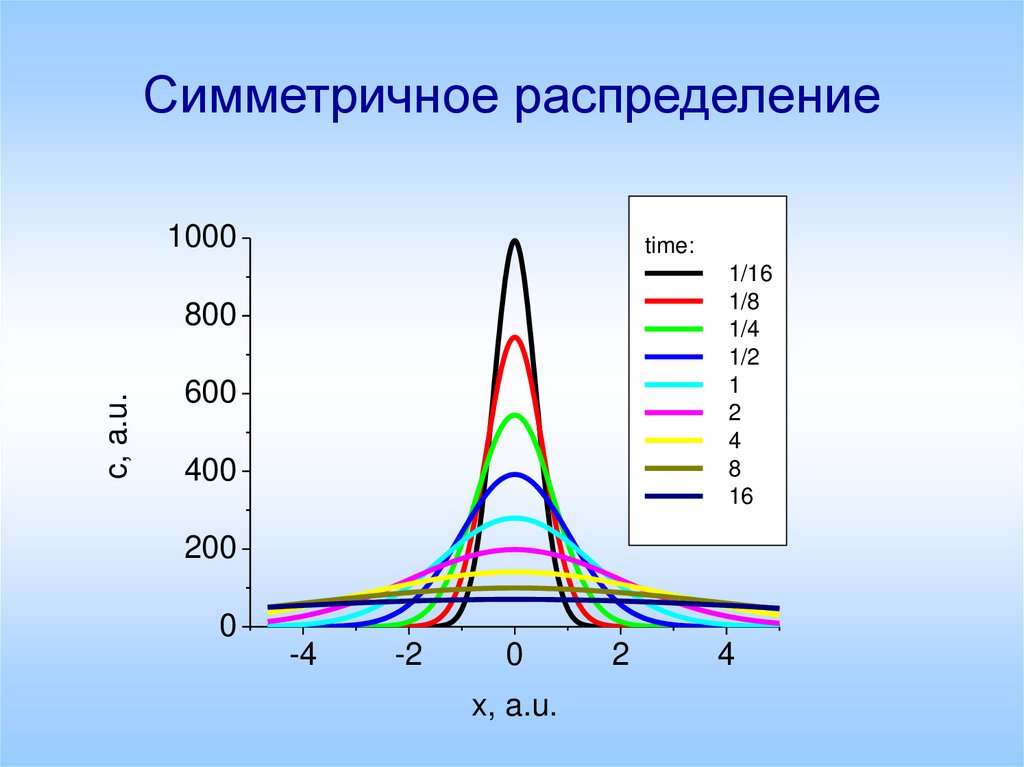
11. Симметричное распределение

1000
time:
1/16
1/8
1/4
1/2
1
2
4
8
16
c, a.u.
800
600
400
200
0
-4
-2
0
x, a.u.
2
4

12. Симметричное распределение

• Поток через плоскость x = 0:
( x) 2
c
1
d
c( ,0)( x) exp
x 2Dt 4 Dt
4 Dt
2
c
1
d 0
c( ,0) exp
x x 0 2 Dt 4 Dt
4 Dt
• (интеграл нечетной функции в симметричных
пределах)

13. Симметричное распределение

( x) 2
1
d
c ( x, t )
c( ,0) exp
4 Dt
4 Dt
0
( x )2
( x )2
1
d c( ,0) exp
d
c( ,0) exp
4 Dt
4 Dt
4 Dt
0
( x )2
( x z)2
( x z)2
c( ,0) exp 4Dt d 0 c( z,0) exp 4Dt dz 0 c( z,0) exp 4Dt dz
0
( x )2
( x ) 2
1
exp
d
c ( x, t )
c( ,0) exp
4 Dt
4 Dt
4 Dt 0

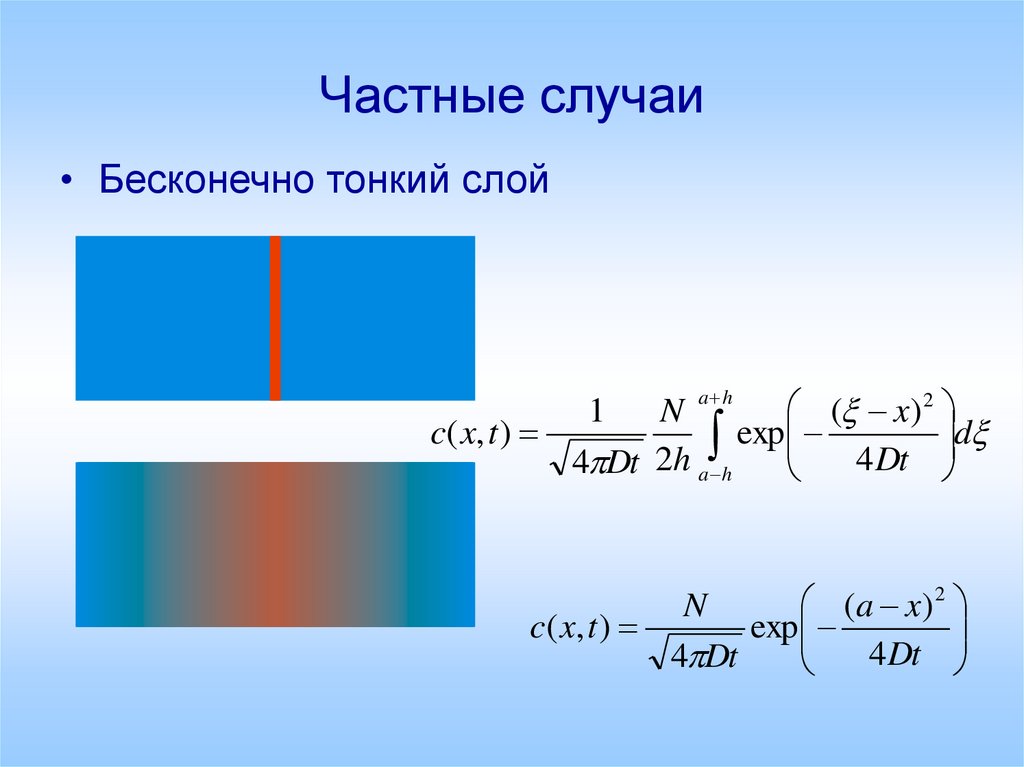
14. Частные случаи

• Бесконечно тонкий слой
a h
( x) 2
1
N
d
c( x, t )
exp
4 Dt
4 Dt 2h a h
( a x) 2
N
c( x, t )
exp
4 Dt
4 Dt

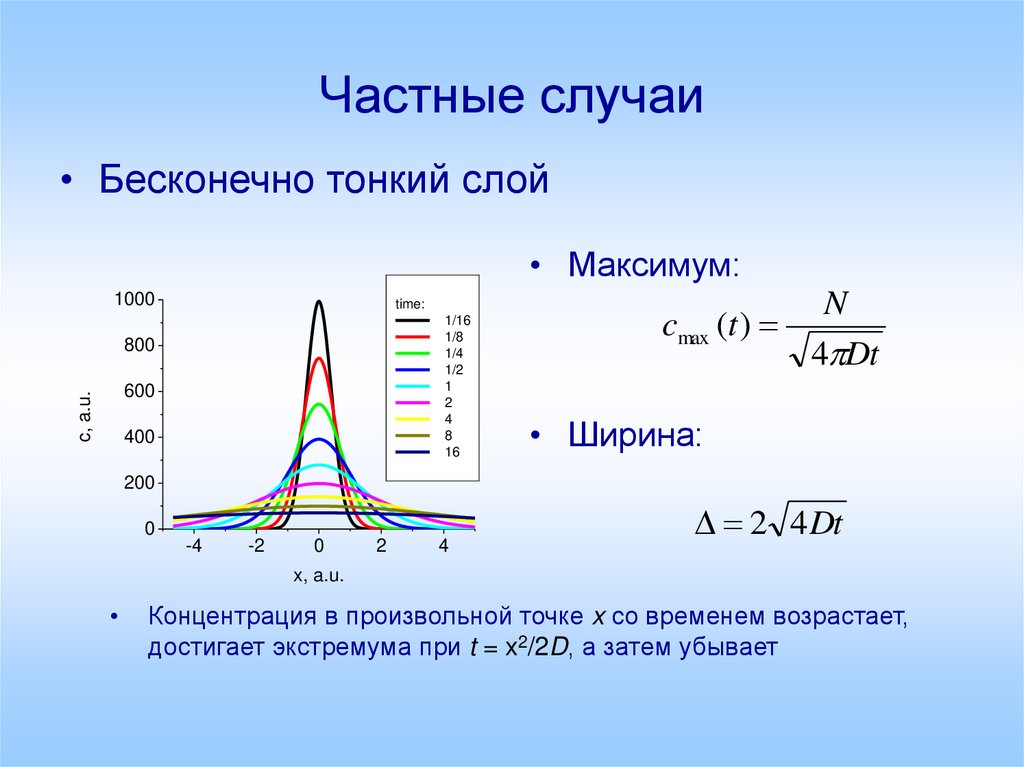
15. Частные случаи

• Бесконечно тонкий слой
• Максимум:
1000
time:
1/16
1/8
1/4
1/2
1
2
4
8
16
800
c, a.u.
600
400
N
cmax (t )
4 Dt
• Ширина:
200
0
-4
-2
0
2
4
2 4Dt
x, a.u.
Концентрация в произвольной точке x со временем возрастает,
достигает экстремума при t = x2/2D, а затем убывает

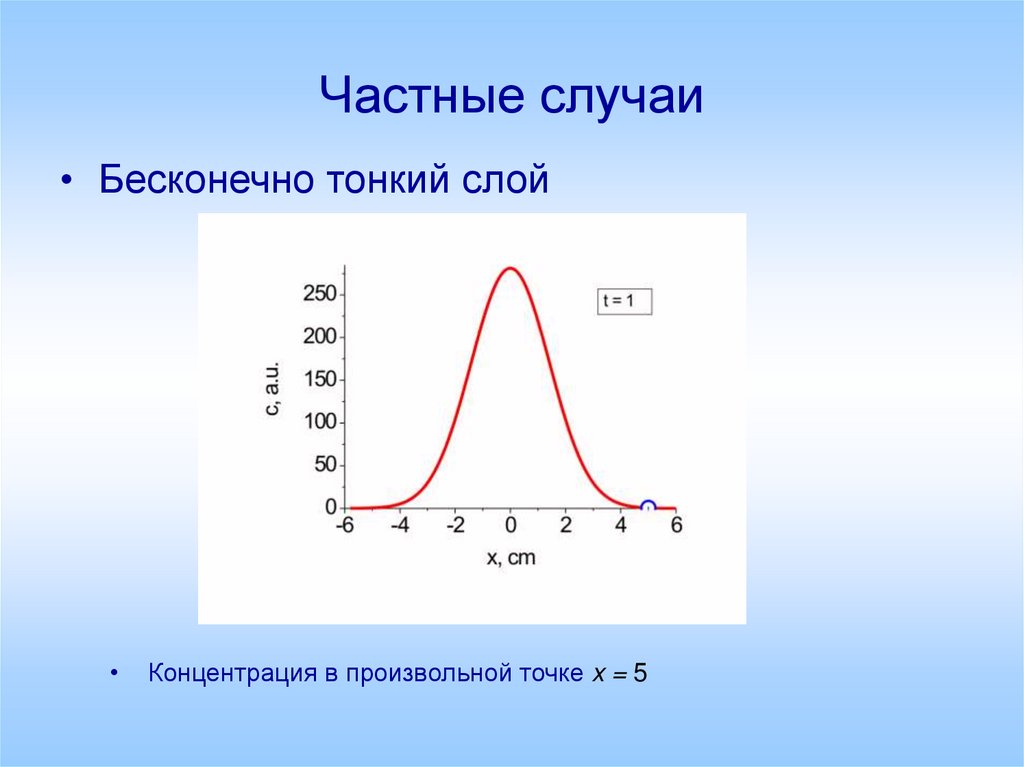
16. Частные случаи

• Бесконечно тонкий слой
Концентрация в произвольной точке x = 5

17. Частные случаи

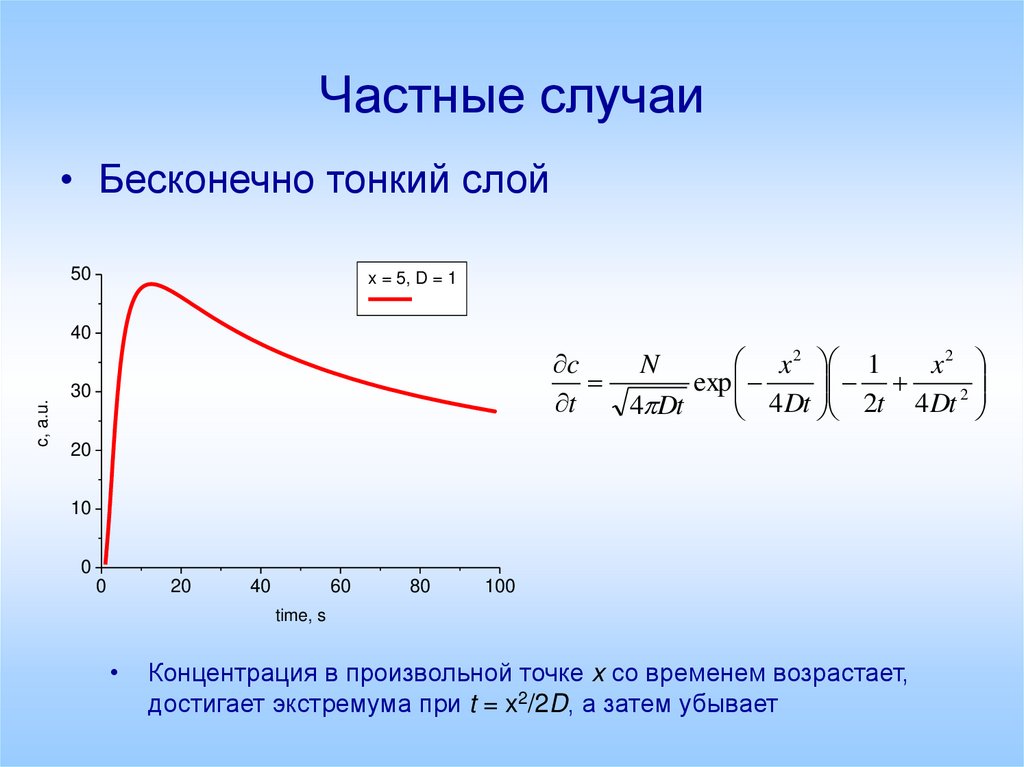
• Бесконечно тонкий слой
50
x = 5, D = 1
c, a.u.
40
x 2 1
c
N
x2
exp
2
t
4 Dt
4 Dt 2t 4 Dt
30
20
10
0
0
20
40
60
80
100
time, s
Концентрация в произвольной точке x со временем возрастает,
достигает экстремума при t = x2/2D, а затем убывает

18. Частные случаи

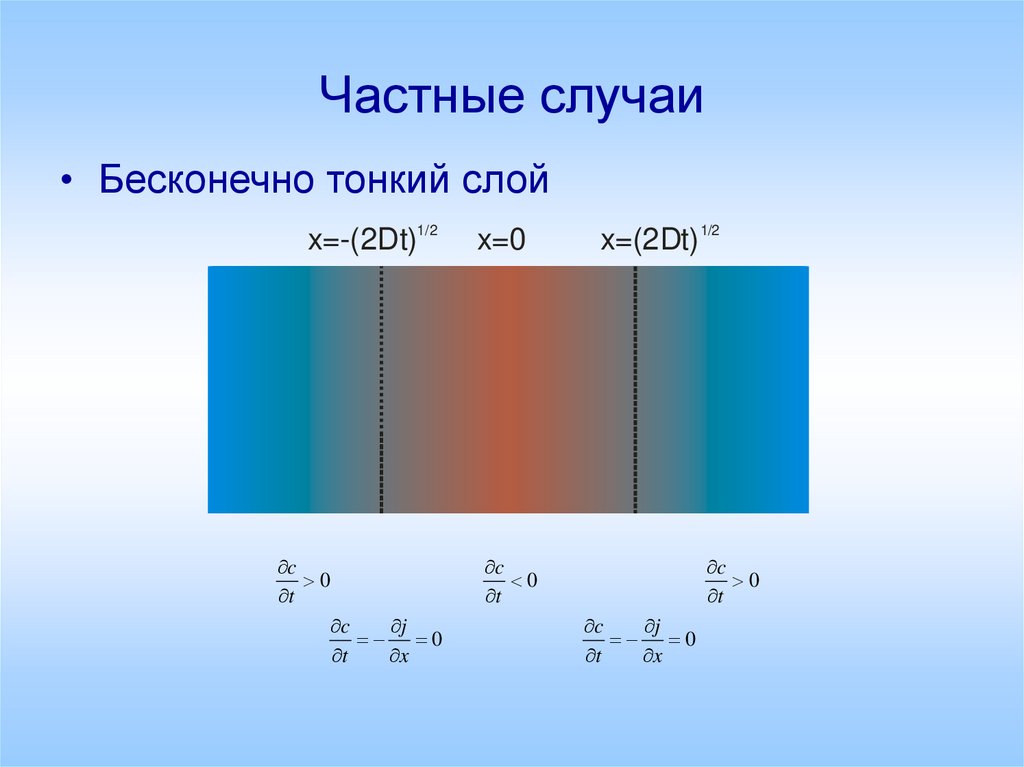
• Бесконечно тонкий слой
x=-(2Dt)1/2
c
0
t
x=0
x=(2Dt) 1/2
c
0
t
c
j
0
t
x
c
0
t
c
j
0
t
x

19. Частные случаи

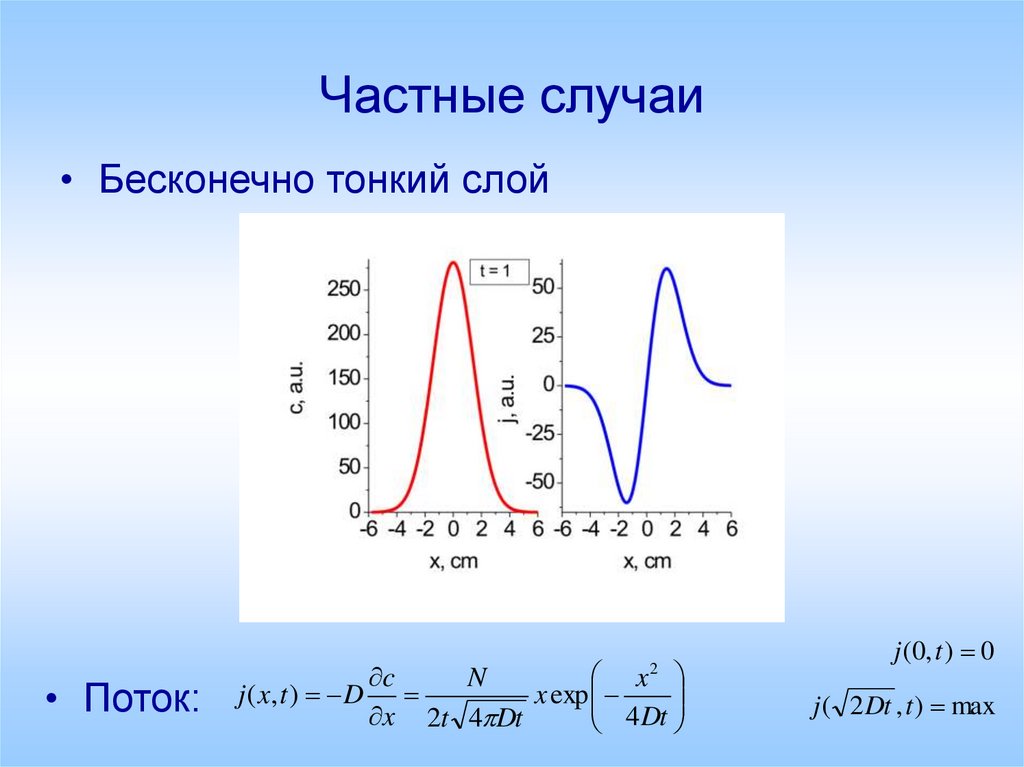
• Бесконечно тонкий слой
• Поток:
j ( x, t ) D
x
c
N
x exp
x 2t 4 Dt
4 Dt
2
j (0, t ) 0
j ( 2 Dt , t ) max

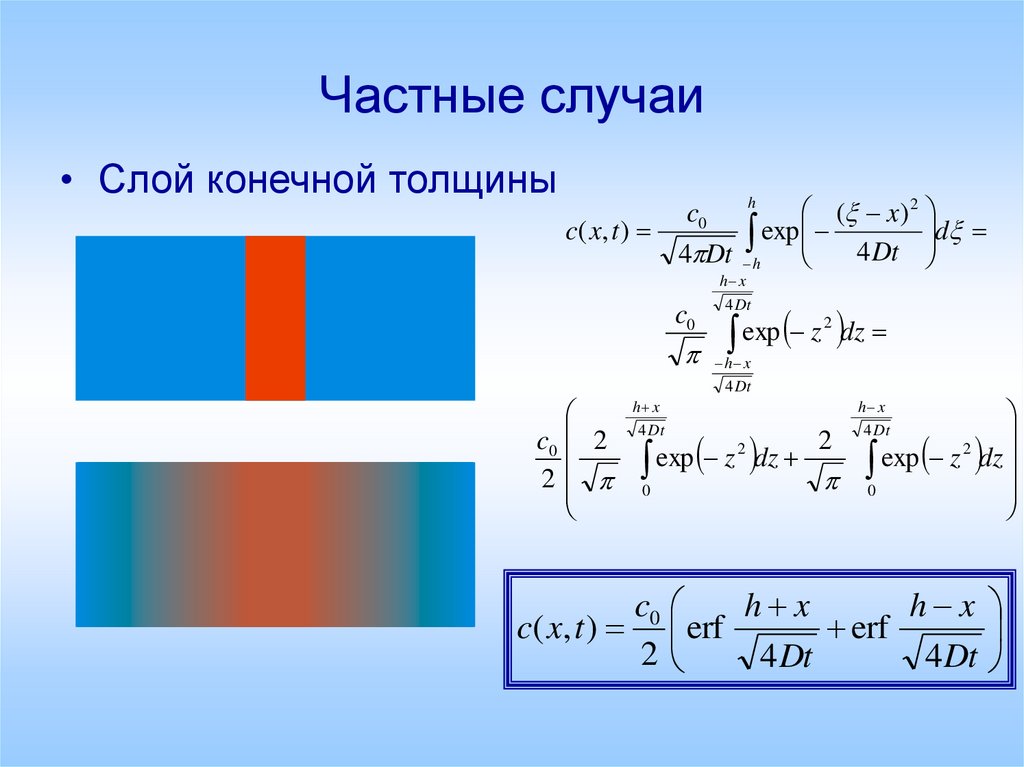
20. Частные случаи

• Слой конечной толщины
h
( x) 2
c0
d
c ( x, t )
exp
4 Dt
4 Dt h
h x
4 Dt
c0
h x
c0 2
2
2
exp
z
dz
4 Dt
h x
4 Dt
2
exp
z
dz
0
2
2
0 exp z dz
h x
4 Dt
c0
h x
h x
c( x, t ) erf
erf
2
4 Dt
4 Dt

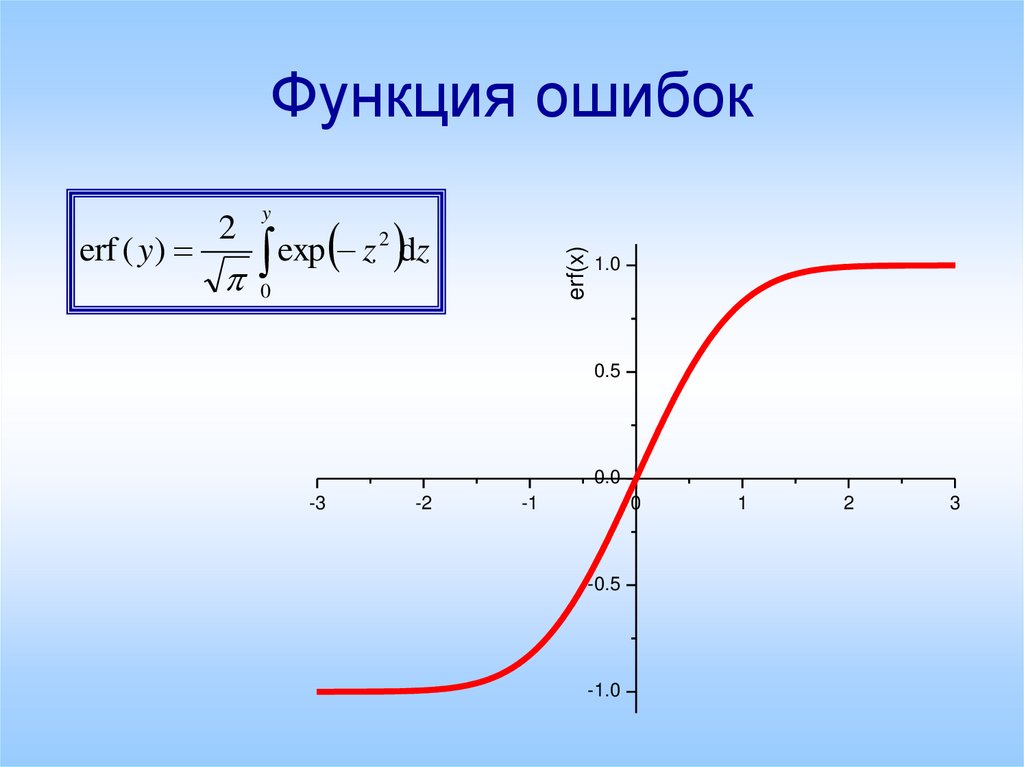
21. Функция ошибок

2
2
dz
exp
z
erf(x)
erf ( y)
y
0
1.0
0.5
0.0
-3
-2
-1
0
-0.5
-1.0
1
2
3

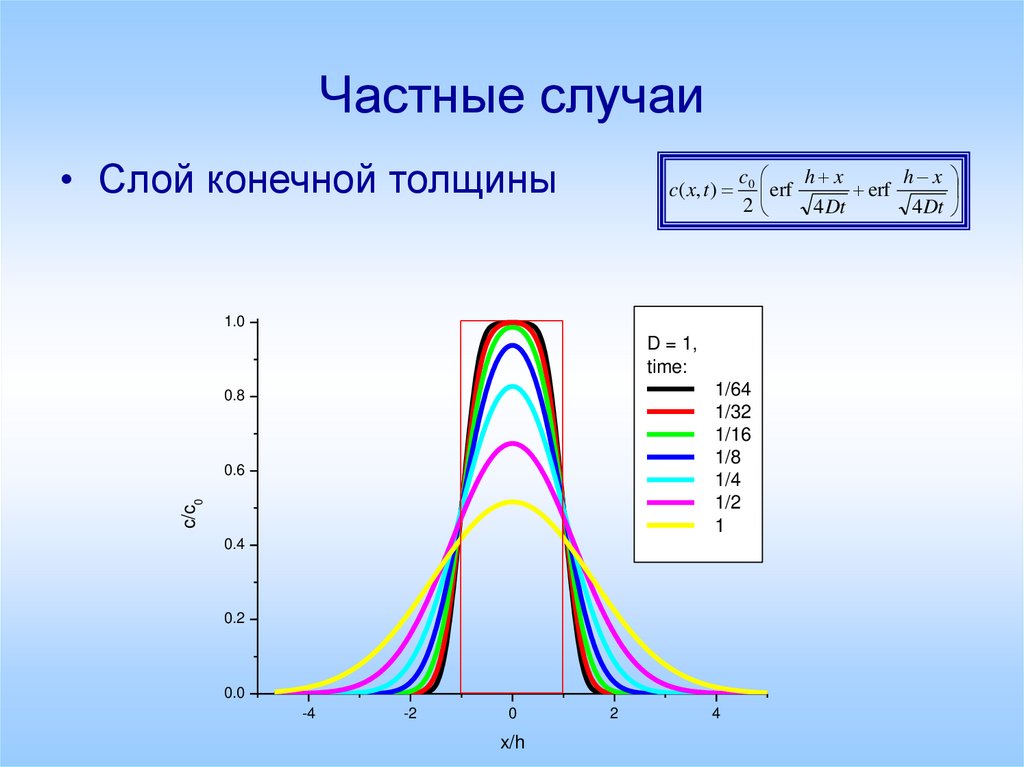
22. Частные случаи

• Слой конечной толщины
c ( x, t )
c0
h x
h x
erf
erf
2
4 Dt
4 Dt
1.0
D = 1,
time:
1/64
1/32
1/16
1/8
1/4
1/2
1
0.8
c/c0
0.6
0.4
0.2
0.0
-4
-2
0
x/h
2
4

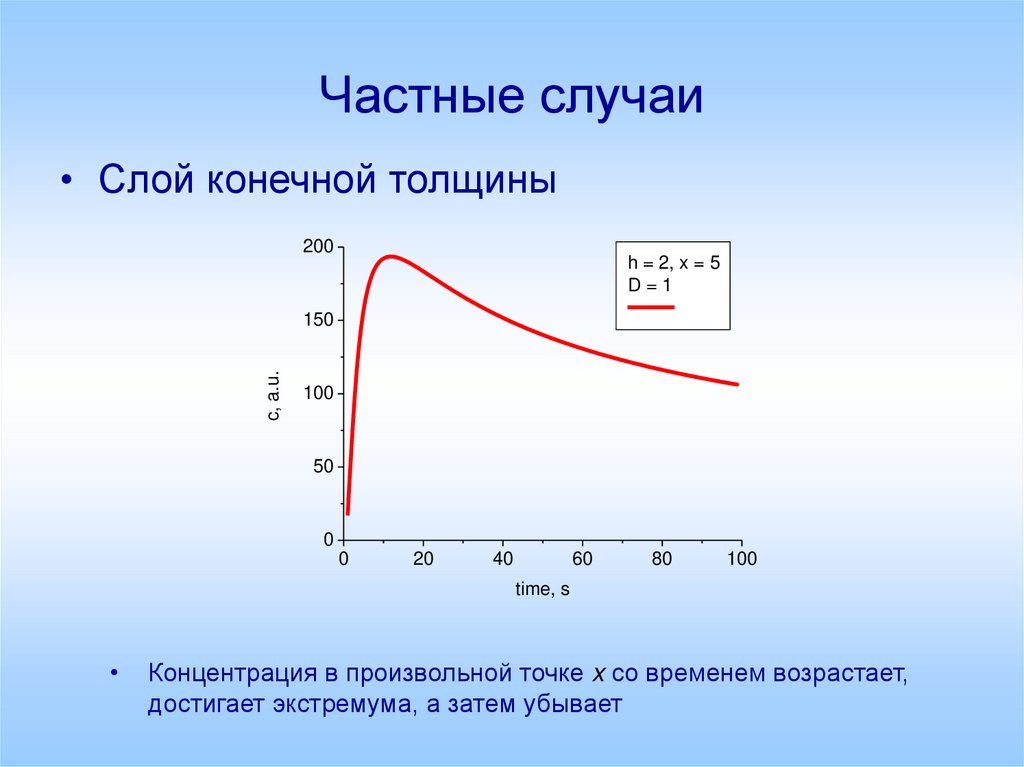
23. Частные случаи

• Слой конечной толщины
200
h = 2, x = 5
D=1
c, a.u.
150
100
50
0
0
20
40
60
80
100
time, s
Концентрация в произвольной точке x со временем возрастает,
достигает экстремума, а затем убывает

24. Частные случаи

• Ступенчатое распределение
0
( x )2
c0
d
c ( x, t )
exp
4 Dt
4 Dt
c0
x
1 erf
2
4 Dt
c0
x
c( x, t ) erfc
2
4 Dt

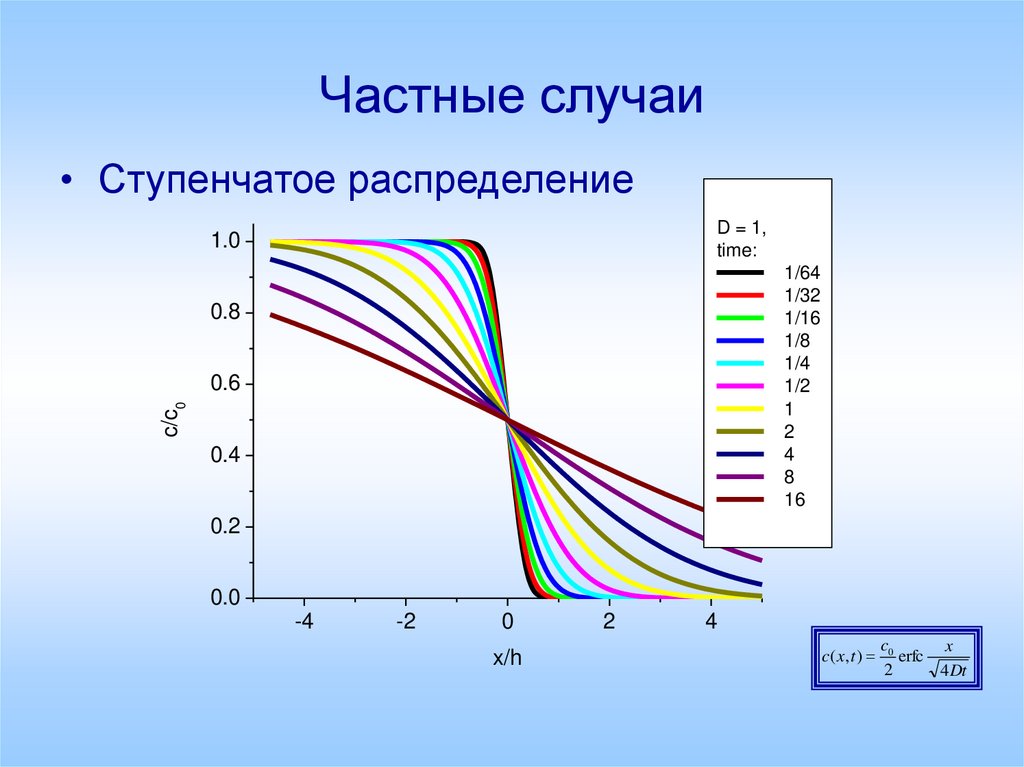
25. Частные случаи

• Ступенчатое распределение
D = 1,
time:
1.0
1/64
1/32
1/16
1/8
1/4
1/2
1
2
4
8
16
0.8
c/c0
0.6
0.4
0.2
0.0
-4
-2
0
x/h
2
4
c ( x, t )
c0
x
erfc
2
4 Dt

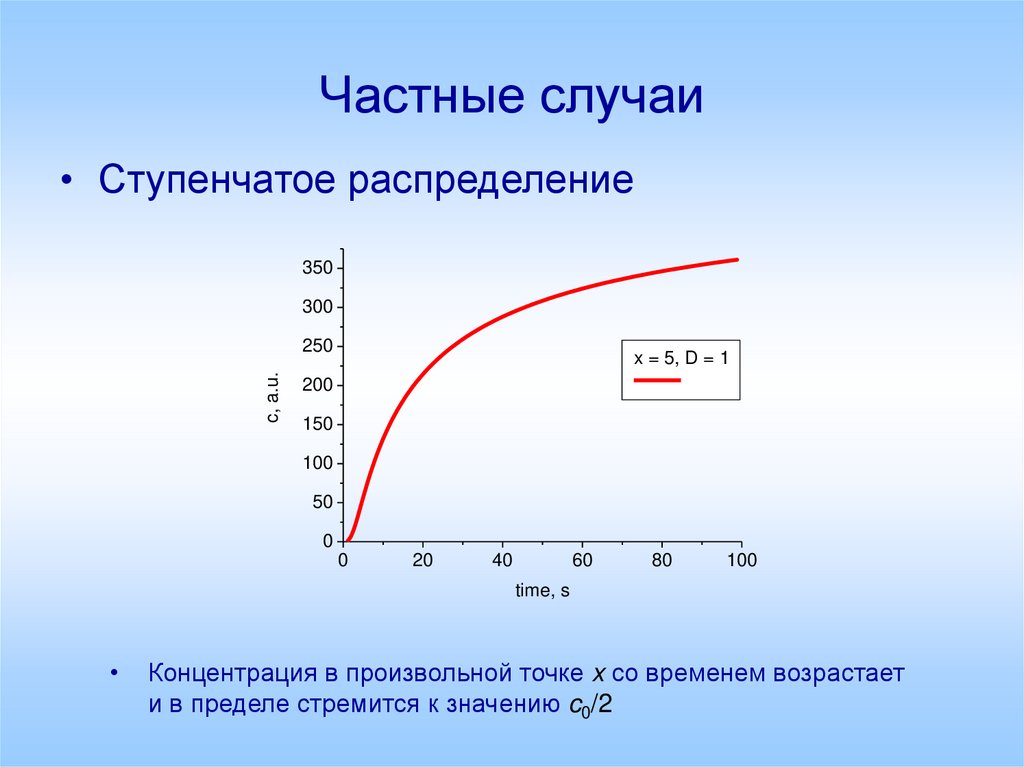
26. Частные случаи

• Ступенчатое распределение
350
300
c, a.u.
250
x = 5, D = 1
200
150
100
50
0
0
20
40
60
80
100
time, s
Концентрация в произвольной точке x со временем возрастает
и в пределе стремится к значению c0/2

27. Диффузия в полуограниченном теле

Граница
Диффузия в полуограниченном теле
0
( x) 2
( x) 2
1
c ( x, t )
c1 ( ,0) exp
d c( ,0) exp
d
4
Dt
4
Dt
4 Dt
0
( x) 2
( x) 2
1
c ( x, t )
c( ,0) exp
c1 ( ,0) exp
d
4
Dt
4
Dt
4 Dt 0
c1 ( ,0) ?
Неизвестная функция должна быть определена из граничных условий

28. Диффузия в полуограниченном теле

• Непроницаемая граница:
c
j (0, t ) D
0
x x 0
( x) 2
( x) 2
c
1
( x)c( ,0) exp
( x)c1 ( ,0) exp
d
x 2 Dt 4 Dt 0
4 Dt
4 Dt
2
c
1
c( ,0) c1 ( ,0) exp
d 0
x x 0 2 Dt 4 Dt 0
4 Dt
c1 ( ,0) c( ,0)
c ( x, t )
( x) 2
( x) 2
1
c( ,0) exp
exp
d
4 Dt
4 Dt
4 Dt 0

29. Диффузия в полуограниченном теле

c(0, t ) c x 0 0
• десорбция:
• (поглощающая граница)
2
1
c( ,0) c1 ( ,0) exp d 0
c(0, t )
4 Dt 0
4 Dt
c1 ( ,0) c( ,0)
c(0, t )
( x) 2
( x) 2
1
exp
d
c( ,0) exp
4 Dt
4 Dt
4 Dt 0

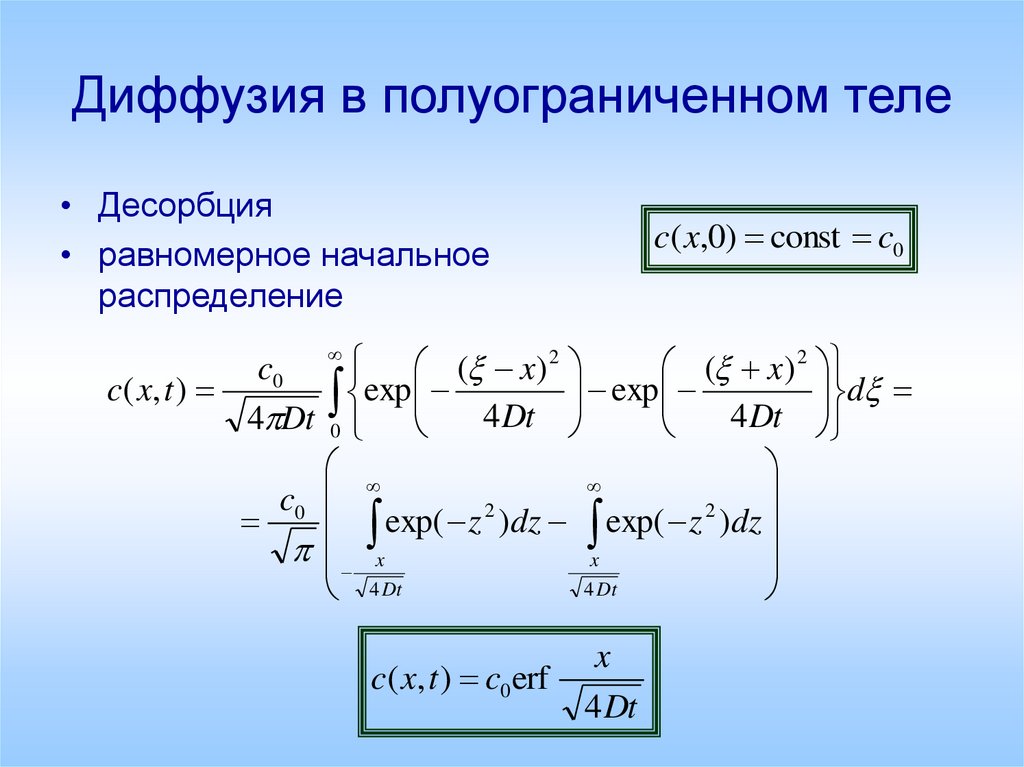
30. Диффузия в полуограниченном теле

• Десорбция
• равномерное начальное
распределение
c( x,0) const c0
( x) 2
( x) 2
c0
exp
d
c ( x, t )
exp
4 Dt
4 Dt
4 Dt 0
c0
2
2
exp( z )dz exp( z )dz
x
x
4 Dt
4 Dt
c( x, t ) c0erf
x
4 Dt

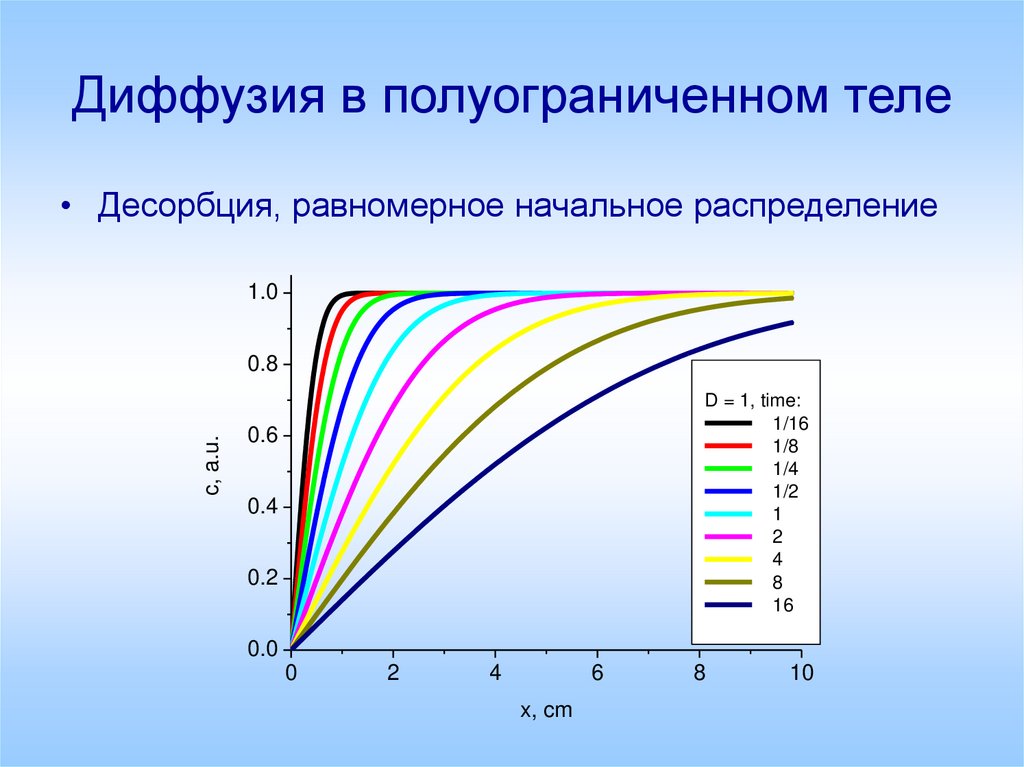
31. Диффузия в полуограниченном теле

• Десорбция, равномерное начальное распределение
1.0
c, a.u.
0.8
D = 1, time:
1/16
1/8
1/4
1/2
1
2
4
8
16
0.6
0.4
0.2
0.0
0
2
4
6
x, cm
8
10

32. Диффузия в полуограниченном теле

• Десорбция, равномерное начальное распределение

33. Диффузия в полуограниченном теле

• Десорбция, равномерное начальное распределение
• Поток:
x2
Dc0
c
D
c0
j ( x, t ) x 0 D
exp
x x 0
t
Dt
4 Dt x 0
• Число частиц, покинувших тело:
t
N (t ) j ( x, t )
0
dt c0
x 0
4 Dt