Похожие презентации:
Нагрев материалов лазерным излучением
1. Лекция 3. Нагрев материалов лазерным излучением
1ЛЕКЦИЯ 3. НАГРЕВ МАТЕРИАЛОВ
ЛАЗЕРНЫМ ИЗЛУЧЕНИЕМ
2. Общая характеристика нагревания лазерным излучением
ОБЩАЯ ХАРАКТЕРИСТИКА НАГРЕВАНИЯ ЛАЗЕРНЫМИЗЛУЧЕНИЕМ
Лазерный нагрев по своей физической сущности не отличается от других видов нагрева.
Однозначной характеристикой теплового действия является температура, а сам нагрев
состоит в увеличении амплитуды тепловых колебаний решетки
Перенос тепла в твердом теле осуществляется механизмами теплопроводности.
Для металлов и сильно вырожденных полупроводников основным является
электронная теплопроводность, а для неметаллов – решеточная.
Особенности лазерного нагрева:
1. Высокие градиенты температуры
T
x
109 / м
T
2. Высокие скорости нагрева и охлаждения
t
1013 K / c
2
Высокие скорости нагревания и охлаждения и большие пространственные градиенты
температуры обуславливают особенности лазерного нагрева и могут привести и
приводят к значительным отличиям в протекании тепловых процессов,
стимулированных лазерным воздействием.
3. Общая характеристика нагревания лазерным излучением
ОБЩАЯ ХАРАКТЕРИСТИКА НАГРЕВАНИЯ ЛАЗЕРНЫМИЗЛУЧЕНИЕМ
Результат теплового действия лазерного излучения будет определяться следующими
группами параметров:
1. Параметры нагревающего излучения
Плотность мощности q
Длительность импульса τ
Форма и размер зоны облучения (радиус пучка в зоне обработки r0)
….
2. Оптические характеристики материала
Поглощательная способность A
Коэффициент поглощения α
3. Теплофизические характеристики материала
3
Удельная теплоемкость c
Коэффициент теплопроводности k
4. Основные теплофизические понятия
ОСНОВНЫЕ ТЕПЛОФИЗИЧЕСКИЕ ПОНЯТИЯ1. Удельная теплоемкость – показывает количество теплоты, которое необходимо
сообщить единице объема (массы) материала, чтобы нагреть его на один градус.
сV
dQ
dVdT
- теплоемкость единицы объема [ Дж/(м3·K)].
сm
Q
m T
- теплоемкость единицы массы [Дж/(кг·K)].
сV cm
(ρ - плотность)
В дальнейшем c = cV.
2. Тепловой поток – количество тепла проходящее в единицу времени через
изотермическую поверхность и отнесенное к единице площади изотермической
поверхности.
dQ
n – единичная нормаль к изотермической поверхности,
jQ n
dtdS
направленная в сторону уменьшения температуры.
4
Необходимым условием наличия теплового потока является наличие
температурного
градиента.
Опыт
показывает,
что
передача
тепла
теплопроводностью происходит по нормали к изотермической поверхности от
мест с большей температурой к местам с меньшей температурой.
5. Основные теплофизические понятия
ОСНОВНЫЕ ТЕПЛОФИЗИЧЕСКИЕ ПОНЯТИЯ3. Коэффициент теплопроводности
Закон Фурье: величина теплового потока в некоторой точке прямо
пропорциональна градиенту температур в этой точке.
Коэффициент
пропорциональности
называется
коэффициентом
теплопроводности.
jQ k gradT
k – коэффициент теплопроводности [Вт/(м·K)]
4. Коэффициент температуропроводности
k
- коэффициент температуропроводности [м2/с]
c
В отличие от теплопроводности k , которая характеризует способность
материала проводить тепло, температуропроводность a
характеризует
распространение по веществу волны температуры.
a
5. Плотность мощности объемных источников тепла (объемная плотность
мощности тепловых источников) – энергия, выделяемая в виде тепла за единицу
времени в единице объема среды.
dQ
dtdV
- плотность мощности объемных источников тепла [Вт/м3]
5
qv
6. Связь qv с законом поглощения излучения в материале
СВЯЗЬ qv С ЗАКОНОМ ПОГЛОЩЕНИЯ ИЗЛУЧЕНИЯ ВМАТЕРИАЛЕ
q(x) – закон убывания плотности мощности в материале. qv - ?
Энергия ΔQ выделившаяся в слое
между плоскостями x и x + Δx за
время Δt равна:
Q q ( x) S t q ( x x) S t
qv
qv
q ( x)
x
Q
q ( x)
S t x x 0
x
- объемная плотность мощности тепловых источников,
обусловленная поглощением излучения по закону q(x) равна
производной q(x) по x взятой с обратным знаком.
Обычно справедлив закон Бугера: q ( x) Aq0 exp x
6
qv ( x) A q0 exp x
7. Уравнение теплопроводности
УРАВНЕНИЕ ТЕПЛОПРОВОДНОСТИРассуждая аналогичным образом можно показать, что
сообщенное единице объема среды в единицу времени равно:
jQ
dQ
qv
dVdt
x
С другой стороны:
По закону Фурье:
jQ k
количество теплоты
dQ
dT
c
dVdt
dt
T
x
Окончательно получим уравнение теплопроводности:
T
2T
с
k 2 qv
t
x
или
T
2T qv
a 2
t
x
c
Обобщение на трехмерный случай c непостоянными коэффициентами:
c
T
div kgradT qv
t
7
Здесь T = T(r, t), коэффициенты c, k и объемный источник qv могут быть
функциями координат, времени и температуры.
8. Начальные и граничные условия
НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯДля того чтобы получить однозначное решение уравнения теплопроводности
необходимо задать начальные и граничные условия.
Начальное условие для уравнения теплопроводности обычно состоит в задании
температуры в начальный момент времени во всех точках облучаемого лазерным
излучением образца.
T x, 0 T0 x (обычно T0 постоянна по объему и равна комнатной температуре)
Если процесс реагирует только на перепад температуры, то можно принять T0 = 0.
Если процесс «ощущает» абсолютную температуру, то нельзя считать T0 = 0.
Граничные условия определяют условия теплового взаимодействия тела с
окружающей средой, могут быть заданы в различной форме в зависимости от
характера теплообмена с окружающей средой.
8
Выделяют 3 типа граничных условий:
1. граничные условия 1-го рода
2. граничные условия 2-го рода
3. граничные условия 3-го рода
9. Начальные и граничные условия
НАЧАЛЬНЫЕ И ГРАНИЧНЫЕ УСЛОВИЯГраничные условия 1-го рода заключаются в задании распределения
температуры на поверхности тела во все моменты времени.
Ts(t) - некоторая заданная функция (возможно, что Ts(t) = const)
T 0, t Ts t
Граничные условия 2-го рода задают значения плотности теплового потока для
каждой точки поверхности тела:
T
qS (t )
x x 0
Для теплоизолированной поверхности qs = 0
k
При лазерном воздействии для сильно поглощающих сред (большие α) источник
можно считать не объемным а поверхностным, тогда qs = Aq0.
Вклад в qs может быть отрицательным (-ql) если есть тепловые потери,
связанные радиационным или конвективным теплообменом.
При лазерных воздействиях как правило Aq0 >> ql
Если заданы температура окружающей среды Tcр и закон теплообмена между
окружающей средой и поверхностью обрабатываемого материала, то говорят, что
в тепловой задаче заданы граничные условия III рода.
T
x
x 0
T Tср
β – коэффициент теплопередачи [Вт/(м2·K)]
9
k
10. Методы решения уравнения теплопроводности
МЕТОДЫ РЕШЕНИЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ1. Метод интегральных преобразований (операционный метод).
Операционный метод основан на преобразовании искомой функции T(x, t) по
одной из переменных, причем это преобразование (обычно используется
преобразование Лапласа по времени) выбирается с таким расчетом, чтобы
уравнение для новой (преобразованной) функции было значительно проще
исходного. Находят решение преобразованного уравнения, а затем, применяя
к нему обратное преобразование, определяют решение исходного уравнения.
2. Метод источников (метод функций Грина)
Идея метода состоит в том, что сначала находят специальное решение краевой
задачи теплопроводности того же типа (так называемую функцию Грина) , но
более простое. Через него определяют интегральное представление решения
исходной задачи. Функция Грина описывает влияние мгновенного точечного
теплового
источника
на
температурное
поле. Решение задачи для
произвольного источника получается суммированием (интегрированием) вкладов
от точечных источников.
10
3. Численные методы решения
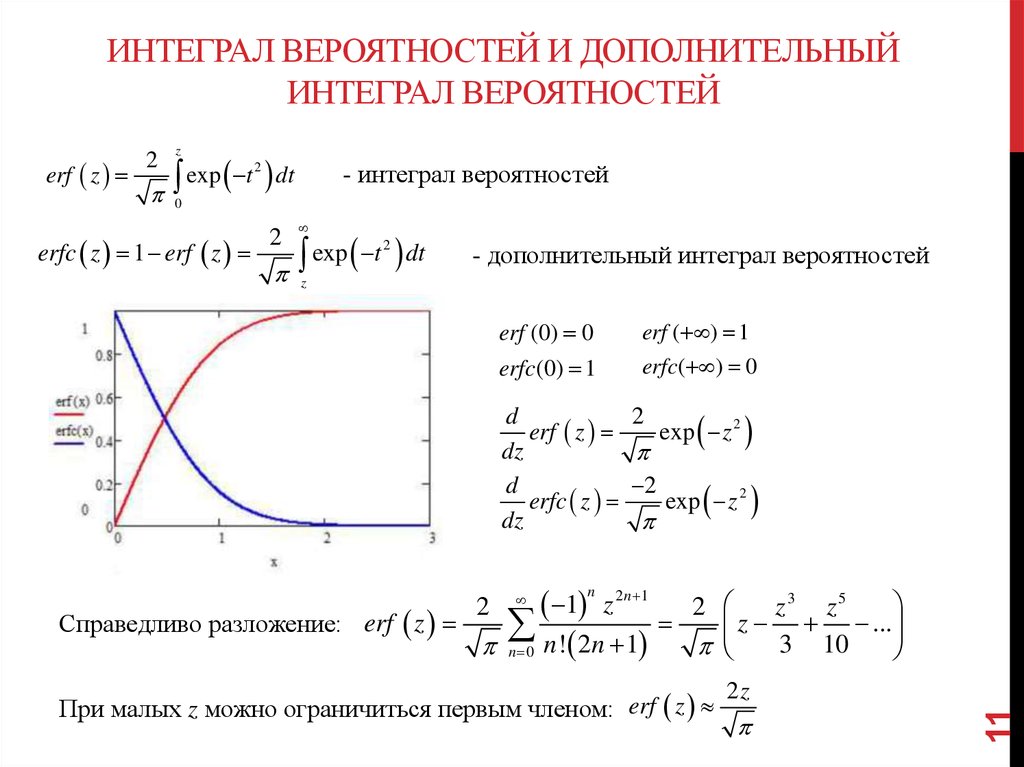
11. интеграл вероятностей и дополнительный интеграл вероятностей
ИНТЕГРАЛ ВЕРОЯТНОСТЕЙ И ДОПОЛНИТЕЛЬНЫЙИНТЕГРАЛ ВЕРОЯТНОСТЕЙ
z
exp t dt
- интеграл вероятностей
2
0
erfc z 1 erf z
2
exp t dt
2
- дополнительный интеграл вероятностей
z
erf (0) 0
erf ( ) 1
erfc(0) 1
erfc( ) 0
d
erf z
dz
d
erfc z
dz
Справедливо разложение: erf z
2
2
exp z 2
exp z 2
1 z 2 n 1 2
n 0 n ! 2n 1
2
n
При малых z можно ограничиться первым членом: erf z
z3 z5
z
...
3 10
2z
11
erf z
2
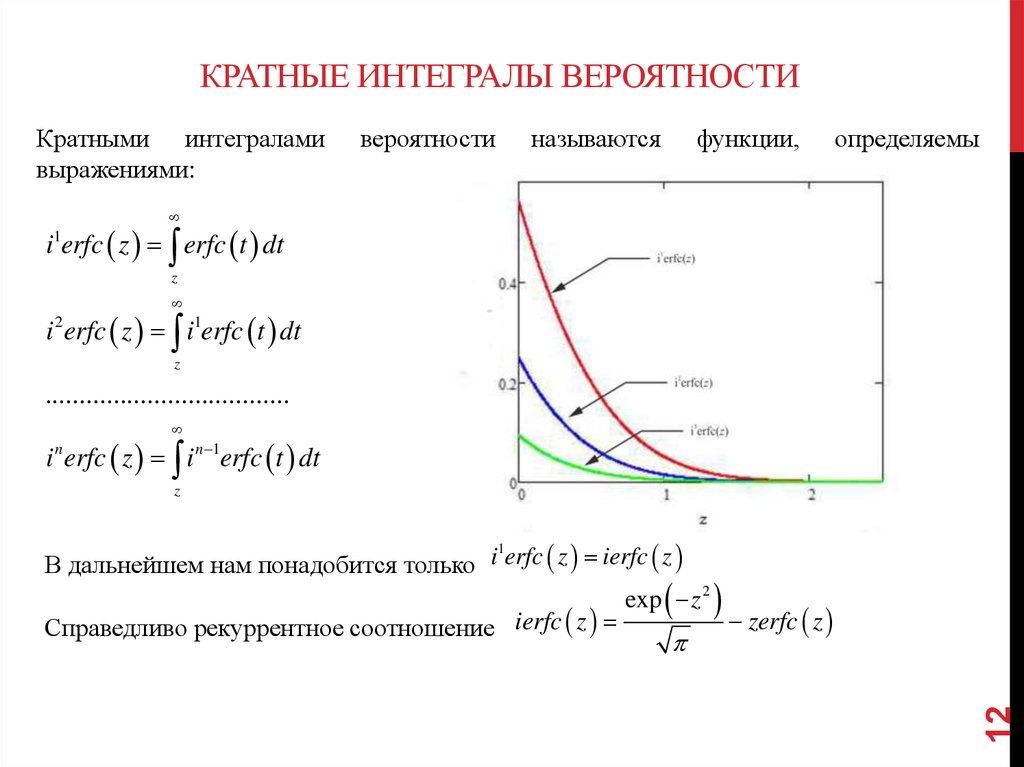
12. Кратные интегралы вероятности
КРАТНЫЕ ИНТЕГРАЛЫ ВЕРОЯТНОСТИКратными интегралами
выражениями:
вероятности
называются
функции,
определяемы
i erfc z erfc t dt
1
z
i erfc z i1erfc t dt
2
z
....................................
i erfc z i n 1erfc t dt
n
z
12
1
В дальнейшем нам понадобится только i erfc z ierfc z
exp z 2
zerfc z
Справедливо рекуррентное соотношение ierfc z
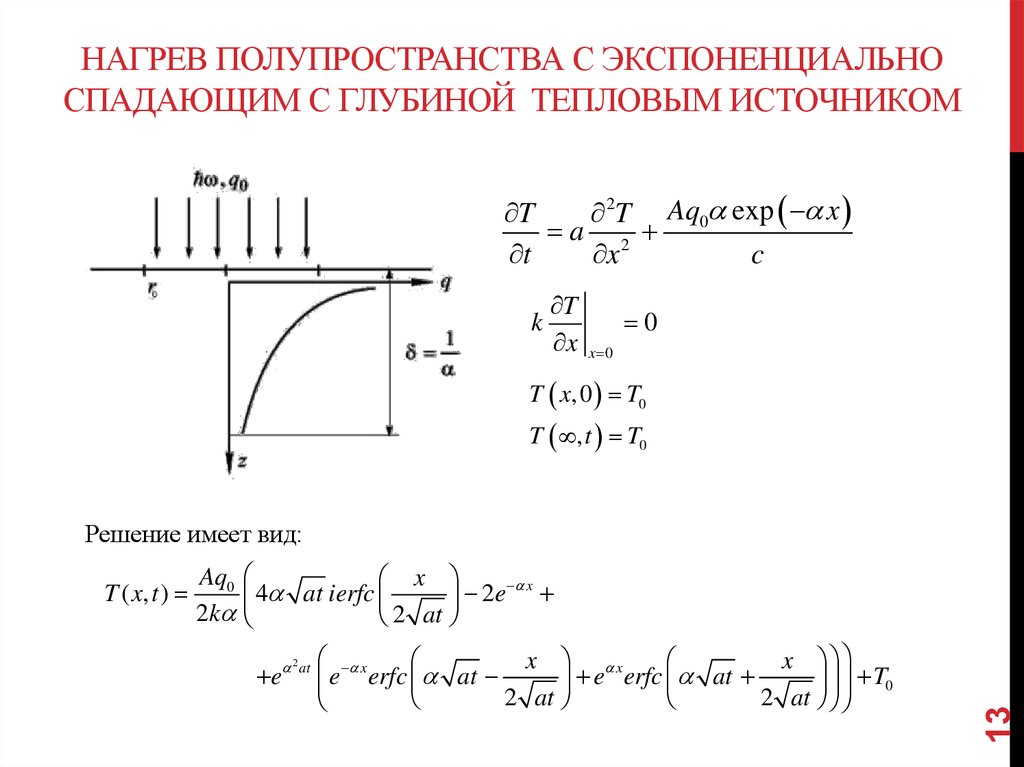
13. Нагрев полупространства с экспоненциально спадающим с глубиной тепловым источником
НАГРЕВ ПОЛУПРОСТРАНСТВА С ЭКСПОНЕНЦИАЛЬНОСПАДАЮЩИМ С ГЛУБИНОЙ ТЕПЛОВЫМ ИСТОЧНИКОМ
T
2T Aq0 exp x
a 2
t
x
c
k
T
x
0
x 0
T x, 0 T0
T , t T0
Решение имеет вид:
Aq0
x
4
at
ierfc
2k
2 at
2 at
e
x
2e
x
x
e
erfc
at
2 at
x
x
e erfc at
T0
2
at
13
T ( x, t )
14. Нагрев полупространства с экспоненциально спадающим с глубиной тепловым источником
НАГРЕВ ПОЛУПРОСТРАНСТВА С ЭКСПОНЕНЦИАЛЬНОСПАДАЮЩИМ С ГЛУБИНОЙ ТЕПЛОВЫМ ИСТОЧНИКОМ
На поверхности:
T (0, t )
Aq0
k
2
at exp 2 at erfc at 1 T0
Рассмотрим 2 предельных случая:
1. Теплопроводность ещё не работает (короткие длительности воздействия)
at
at
at
exp 2 1 2
at
2 at
erfc
1
T (0, t )
Aq0t
T0
c
- адиабатический нагрев
x
Aq0 exp
T
t
c
x
Aq0 exp t
T
T x, t
0
c
14
Это решение может быть получено сразу из уравнения:
15. Нагрев полупространства с экспоненциально спадающим с глубиной тепловым источником
НАГРЕВ ПОЛУПРОСТРАНСТВА С ЭКСПОНЕНЦИАЛЬНОСПАДАЮЩИМ С ГЛУБИНОЙ ТЕПЛОВЫМ ИСТОЧНИКОМ
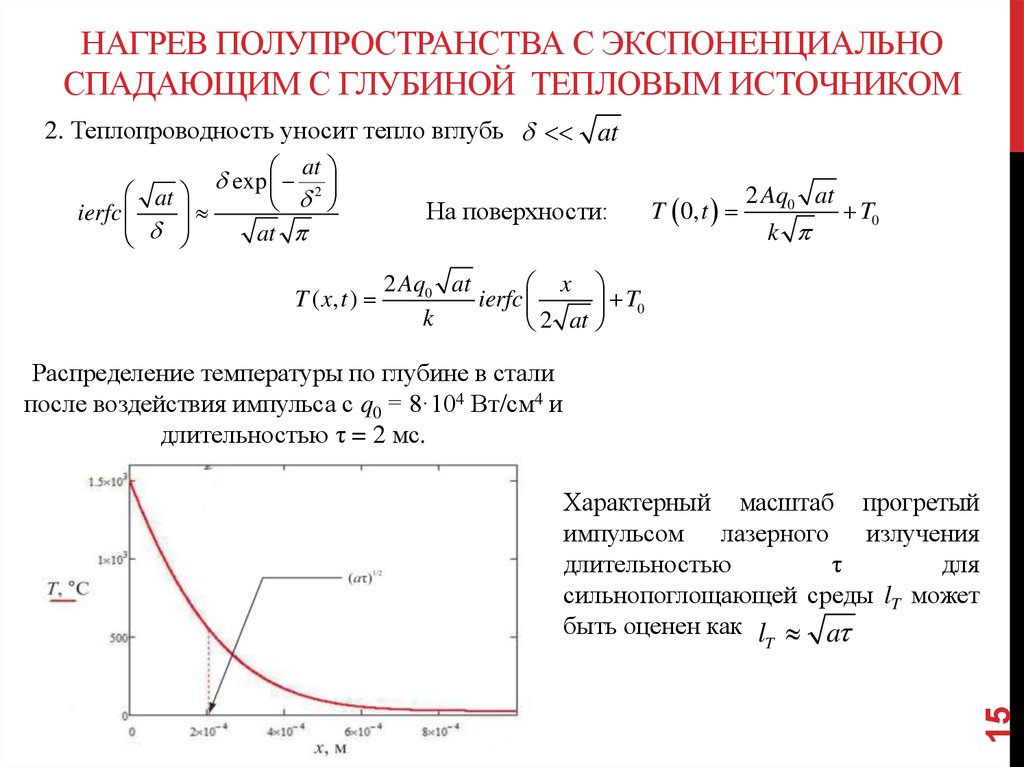
2. Теплопроводность уносит тепло вглубь at
at
ierfc
at
2
at
exp
T ( x, t )
На поверхности:
2 Aq0 at
x
ierfc
k
2 at
T 0, t
2 Aq0 at
k
T0
T0
Распределение температуры по глубине в стали
после воздействия импульса с q0 = 8·104 Вт/см4 и
длительностью τ = 2 мс.
Характерный масштаб прогретый
импульсом лазерного излучения
длительностью
τ
для
сильнопоглощающей среды lT может
быть оценен как l a
15
T
16. Нагрев полупространства поверхностным источником тепла
НАГРЕВ ПОЛУПРОСТРАНСТВА ПОВЕРХНОСТНЫМИСТОЧНИКОМ ТЕПЛА
T
2T
a 2
t
x
T
k
Aq0
x x 0
T 0, x T , t T0
На поверхности:
Решение имеет вид:
T ( x, t )
2 Aq0 at
x
ierfc
k
2 at
T0
T 0, t
2 Aq0 at
k
T0
16
Решение то же, что и для экспоненциально спадающего источника при δ→0.
17. Остывание полупространства после нагрева поверхностным источником
ОСТЫВАНИЕ ПОЛУПРОСТРАНСТВА ПОСЛЕ НАГРЕВАПОВЕРХНОСТНЫМ ИСТОЧНИКОМ
Зная, как нагревается полупространство постоянным во времени излучением
можно определить изменение температуры при остывании полупространства
после окончания импульса излучения.
Воспользуемся следующим приемом: в момент окончания импульса включим
отрицательный поток на поверхности равный по величине нагревающему потоку.
После окончания воздействия (t > τ)
распределение
температуры
будет
определяться зависимостью:
x
T ( x, t ) T 0, T0
t
ierfc
2 at
x
t ierfc
T
2 a (t ) 0
На поверхности:
T 0, t
t
T 0, T
0
2
1
1
t
t
17
Используя полученное выражение можно оценивать скорость охлаждения (важно
для закалки).
18. Нагрев материала постоянным лазерным излучением, луч сфокусирован в пятно круглого сечения
НАГРЕВ МАТЕРИАЛА ПОСТОЯННЫМ ЛАЗЕРНЫМИЗЛУЧЕНИЕМ, ЛУЧ СФОКУСИРОВАН В ПЯТНО КРУГЛОГО
СЕЧЕНИЯ
Aq , 0 r r0
q(r ) 0
0, r r0
При
at r0
При
at r0
При
at r0
T (0, 0, t )
2 Aq0 at
r 2 x2
0
ierfc
2 at
T0
T0
k
Aq r
T (0, 0, t ) 0 0 T0
k
T ( z , 0)
Aq0
k
r02 x 2 x T0
устанавливается стационарное распределение температуры.
18
Решение имеет вид:
2 Aq0 at
x
T ( z , 0, t )
ierfc
k
2 at
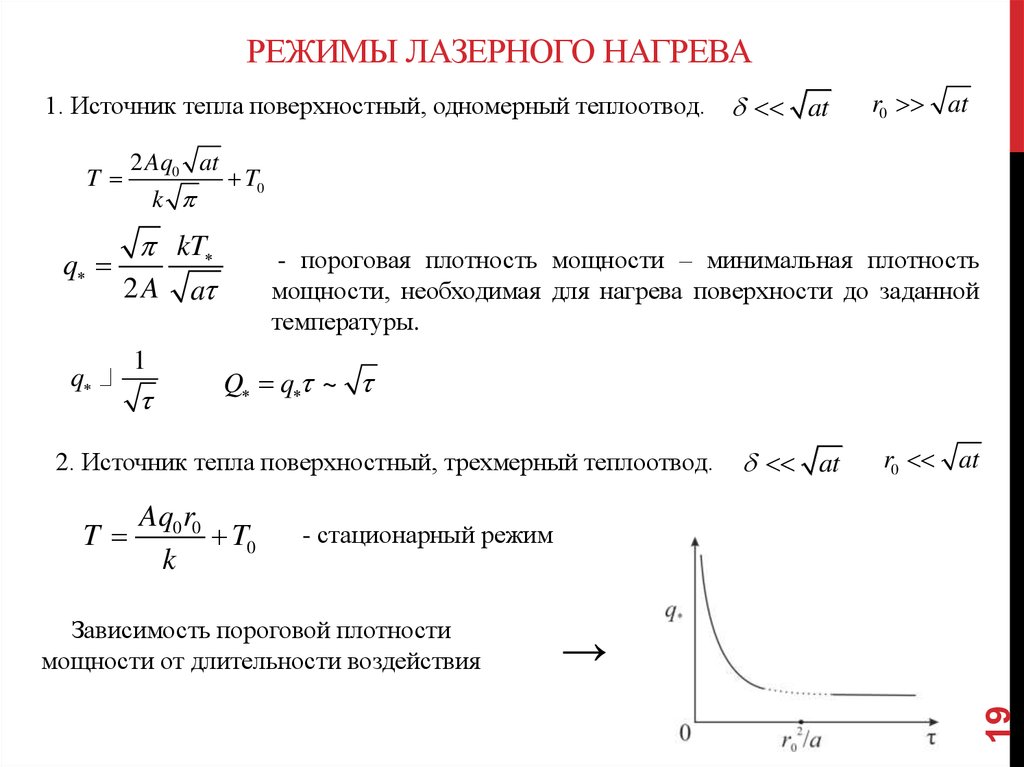
19. Режимы лазерного нагрева
РЕЖИМЫ ЛАЗЕРНОГО НАГРЕВА1. Источник тепла поверхностный, одномерный теплоотвод. at
q
k
T0
kT
2 A a
q
1
- пороговая плотность мощности – минимальная плотность
мощности, необходимая для нагрева поверхности до заданной
температуры.
Q q ~
2. Источник тепла поверхностный, трехмерный теплоотвод.
T
Aq0 r0
T0
k
at
r0 at
- стационарный режим
Зависимость пороговой плотности
мощности от длительности воздействия
→
19
2Aq0 at
T
r0 at
20. Режимы лазерного нагрева
РЕЖИМЫ ЛАЗЕРНОГО НАГРЕВА3. Источник тепла объемный, теплоотвод пренебрежимо мал. at
Температура поверхности T
Aq0
T0
c
4. Источник тепла объемный, трехмерный теплоотвод.
Температура поверхности
r0 at
Aq0 r02
a
T
ln 19.4 2
4 k
r0
at
r0 at
T0
Для металлов характерно поверхностное поглощение, толщина прогретого cлоя при
этом определяется характерным размером теплопроводности (at)1/2.
20
Режимы облучения, обеспечивающие объемное поглощение излучения, используют
при необходимости создать в материале объемный источник тепла, или при
фокусировке излучения внутри объема.
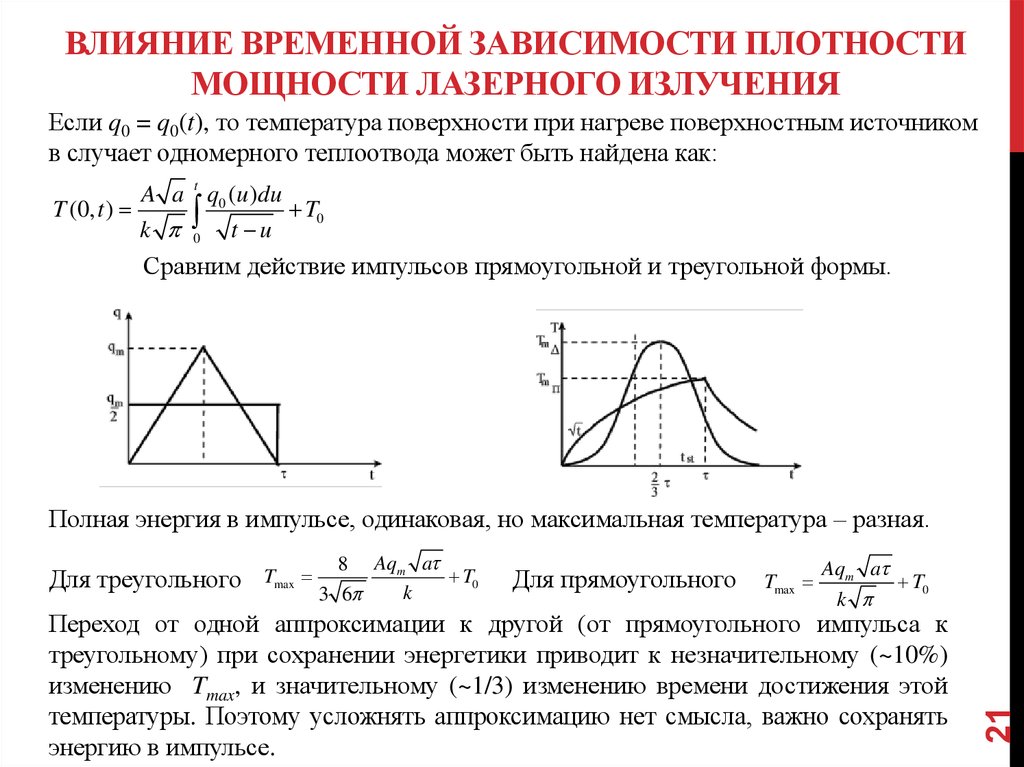
21. Влияние временной зависимости плотности мощности лазерного излучения
ВЛИЯНИЕ ВРЕМЕННОЙ ЗАВИСИМОСТИ ПЛОТНОСТИМОЩНОСТИ ЛАЗЕРНОГО ИЗЛУЧЕНИЯ
Если q0 = q0(t), то температура поверхности при нагреве поверхностным источником
в случает одномерного теплоотвода может быть найдена как:
t
A a q0 (u )du
T (0, t )
T0
k 0 t u
Сравним действие импульсов прямоугольной и треугольной формы.
Полная энергия в импульсе, одинаковая, но максимальная температура – разная.
Tmax
8 Aqm a
T0
k
3 6
Для прямоугольного
Tmax
Aqm a
k
T0
Переход от одной аппроксимации к другой (от прямоугольного импульса к
треугольному) при сохранении энергетики приводит к незначительному (~10%)
изменению Tmax, и значительному (~1/3) изменению времени достижения этой
температуры. Поэтому усложнять аппроксимацию нет смысла, важно сохранять
энергию в импульсе.
21
Для треугольного
22. Особенности нагрева материала движущимся световым пятном
ОСОБЕННОСТИ НАГРЕВА МАТЕРИАЛА ДВИЖУЩИМСЯСВЕТОВЫМ ПЯТНОМ
Распределение
температуры
по
поверхности в движущейся системе
координат имеет вид (на оси):
T ( x)
AP
vx
exp T0
2 kx
2a
P – мощность, v – скорость сканирования
1. Быстродвижущийся источник – воздействие
аналогично
разогреву
полупространства
импульсом с длительностью τ = 2r0/v
T
2Aq0 a
k
T0
T
Aq0 r0
T0
k
22
2. Медленнодвижущийся источник – происходит
стабилизация температуры, поэтому источник
можно считать неподвижным.
23. Лазерный нагрев тонких слоев и пленок
ЛАЗЕРНЫЙ НАГРЕВ ТОНКИХ СЛОЕВ И ПЛЕНОКT1,2
t
a1,2
2T1,2
x 2
f1,2
c1,2
T1
x
T1 ( x, 0) T2 ( x, 0) 0
При x = b
q A
f1 0 1
b
f2
q0 1 R1 A1
2
T1 (b) T2 (b)
k1
e
x
0 T2 , t 0
x 0
T1
x
k2
x b 0
- равенство температур
T2
x
x b 0
2
- равенство потоков
(идеальный тепловой
контакт)
Пленка прогрета равномерно, для T1 справедливо:
c at
a2t c1
c22 a2t
exp 2 2 erfc 1
b
c2
c1 b
c2b
Малые времена воздействия:
Большие времена воздействия:
c1b c2 a2t
1 T0
T1 (t )
T1 (t )
q0 A1t
T0
c1b
2 Aq0 a2t
T0
k2
23
A1q0b 2
T1 (t )
k2
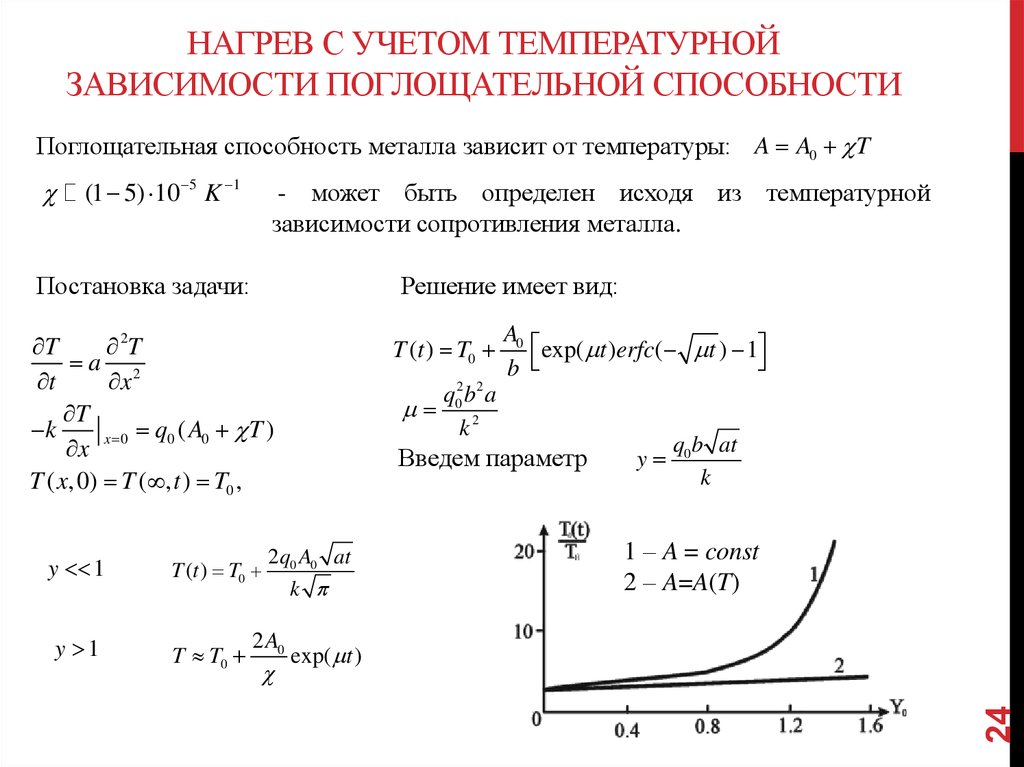
24. Нагрев с учетом температурной зависимости поглощательной способности
НАГРЕВ С УЧЕТОМ ТЕМПЕРАТУРНОЙЗАВИСИМОСТИ ПОГЛОЩАТЕЛЬНОЙ СПОСОБНОСТИ
Поглощательная способность металла зависит от температуры: A A0 T
(1 5) 10 5 K 1
- может быть определен исходя из температурной
зависимости сопротивления металла.
Постановка задачи:
Решение имеет вид:
T
2T
a 2
t
x
T
k
x 0 q0 ( A0 T )
x
T ( x, 0) T ( , t ) T0 ,
y 1
y 1
T (t ) T0
T T0
T (t ) T0
q02b 2 a
2
k
Введем параметр
2q0 A0 at
2 A0
A0
exp( t )erfc( t ) 1
b
k
y
q0b at
k
1 – A = const
2 – A=A(T)
exp( t )
24
25.
25СПАСИБО ЗА ВНИМАНИЕ


















 Физика
Физика








