Распределение частиц по скоростям в плазме

1. Распределение частиц по скоростям в плазме

В отсутствие внешних сил газ
находится в термодинамического
равновесиия, если выполняются условия
теплового и химического равновесия.
Te Ti Ta T
В случае полного термодинамического равновесия спектральная плотность
излучения плазмы совпадает с плотностью излучения черного тела
a1
1
U (T ) 5
exp( a2 ) 1
T
При кинетическом описании процессов в газе или плазме применяются
статистические методы, при которых основной характеристикой
ансамбля частиц принимают функцию распределения частиц по
скоростям (энергиям) f(v).
f (v )dv 1
0
v
vf (v )dv
0

2. Функция распределения

• d = dv·dr = dvx· dvy· dvz· dx· dy· dz.
Функцию распределения частиц определяют из условия, что вероятное число
частиц, находящихся в данный момент времени в элементе объема dr вблизи
точки r и обладающих скоростями v в интервале dv, равно
f(r,v,t)dvdr.
ndr =dr f (v, r,t)dv
n= fdv.
Чтобы характеризовать поведение системы частиц в пространстве и времени,
необходимо знать изменение функции распределения

3. Кинетическое уравнение Больцмана

• Уравнение которому должна
удовлетворять функция
f (r , v , t )
f f qE f
f
v
( ) st
t
r M v
t
Физический смысл функции распределения f состоит в том,
что она характеризует вероятное распределение числа частиц,
обладающих координатами в элементе r + dr и имеющих
скорости в интервале v + dv так, что интеграл от функции
распределения по скоростям дает плотность числа частиц в
окрестностях точки dvdr

4. Уравнене Больцмана- Власова

)

5. Функция распределения Максвелла

2
- Постоянная разделения

6. Функция распределения Максвелла

• . Интегрируя
принимая 1/ 2 =kTe

7. Функция распределения Максвелла

8kT
v vf ( v )dv
m
0
vmax 2kT / m
f ( E ) 2 ( kT )
3 / 2
exp( E / kT ) E

8.

Элементарные процессы в плазме
Элементарные процессы в плазме
ионизация
электронным ударом
рекомбинация
тройная
Изменение числа электронов:
Литература

9.

Коэффициент диффузии
d ( nmVx )
mVx n ei
dt
d ( nVx )
v x n ei
dt
d ( nv x )
d ( nVx )
2 dn
vx
Vx
nVx ei
dt
dx
dx
x nVx
2
V V /3
2
x
2
V
(
) n D n
3 ei
V2
dn
x (
) ср
3 ei dx
2
V
D
3 ei

10. Тройная рекомбинация

11. Подвижность

dv
j t
m m ei v eE0e
dt
e/m
j t
v
E 0e
j em
E const
v E
e
m em

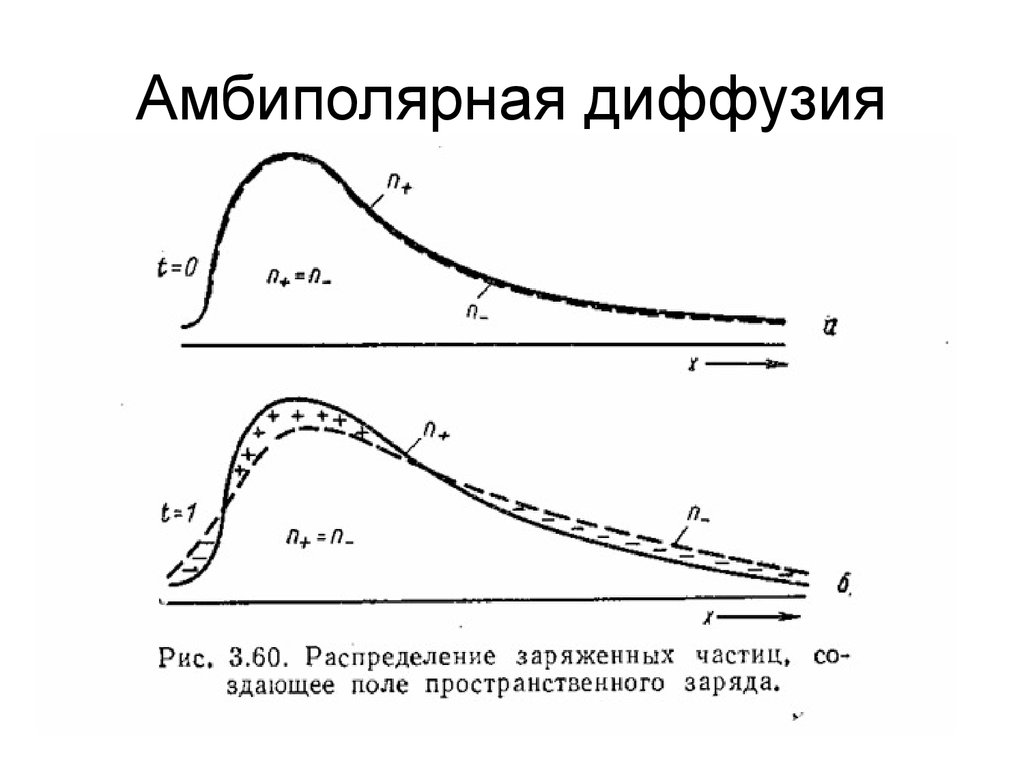
12. Амбиполярная диффузия

13. Амбиполярная диффузия

D n E x n
V
D
n x E x
n
V
D
n E x
n
D D ) n
V (
)
n
D D )
Da
n
Da 2n
t

14. Уравнение диффузии

n
t /
2
D n n( x, y , z , t ) n0 ( x, y , z )e
t
n A1e
t / 1
A2e
1 / 2 3.67
t / 2
A3e
t / 3
....
1 / 3 6.33

15. Цилиндр с плоскими концами

• n=0 на стенках
n n0 cos axJ 0 (br )
a /h
b 2.405 / r
a b 1 / Dt
2
2
Сфера
2
1
r
n n0
exp(
)
3/ 2
( 4 Dt )
4 Dt