Похожие презентации:
Интерполяция. Оценка погрешности методов интерполяции
1. ИНТЕРПОЛЯЦИЯ
2.
На интервале [a, b] задана система точек – узловинтерполяции xi, i=0,1,…,N; a≤xi≤b и значения
неизвестной
функции
в
этих
узлах
fi .
Могут быть поставлены следующие задачи.
1. Построить функцию F(x), принимающую в узлах
интерполяции заданные значения:
F(xi)=fi, i=0,1,…,N (условия интерполяции).
2. Для заданного произвольного значения zϵ[a, b]
найти F(z).
3. Оценка погрешности методов интерполяции
Задача интерполяции имеет множество решений, т.к.через заданные точки (xi, fi ), i=0,1,…,N можно провести
бесконечное число кривых, для которых будут
выполнены все условия интерполяции.
Если известна исходная функция f(x), то погрешность
метода r(z) в произвольной точке zϵ[a, b] можно
оценить по следующему выражению:
r(z)=|f(z) – F(z)|
Погрешность уменьшается при увеличении числа
узлов интерполяции. Будем считать, что метод
сходится, если при N погрешность r 0.
4. Методы интерполяции
Все методы интерполяции можно разделитьна два типа: локальные и глобальные.
В случае локальной интерполяции на
каждом отрезке [xi-1, xi] строится своя
(локальная) функция.
В случае глобальной интерполяции на
всем интервале [a, b] строится одна
(глобальная) функция.
5. ЛОКАЛЬНАЯ ИНТЕРПОЛЯЦИЯ
Кусочно-постоянная интерполяцияКусочно-линейная интерполяция
Кусочно-параболическая интерполяция
Кубический интерполяционный сплайн
6. Кусочно-постоянная интерполяция
[xi-1,xi], i=1,…,Nинтерполирующая функция заменяется константой.
Различают
два
вида
кусочно-постоянной
интерполяции.
На
каждом
локальном
отрезке
1. Левая кусочно-постоянная интерполяция : Fi(z)=fi-1 .
y
fN-1
f0
fi-1
X0
X1
Xi-1
Xi
XN-1
XN
x
7. Кусочно-постоянная интерполяция
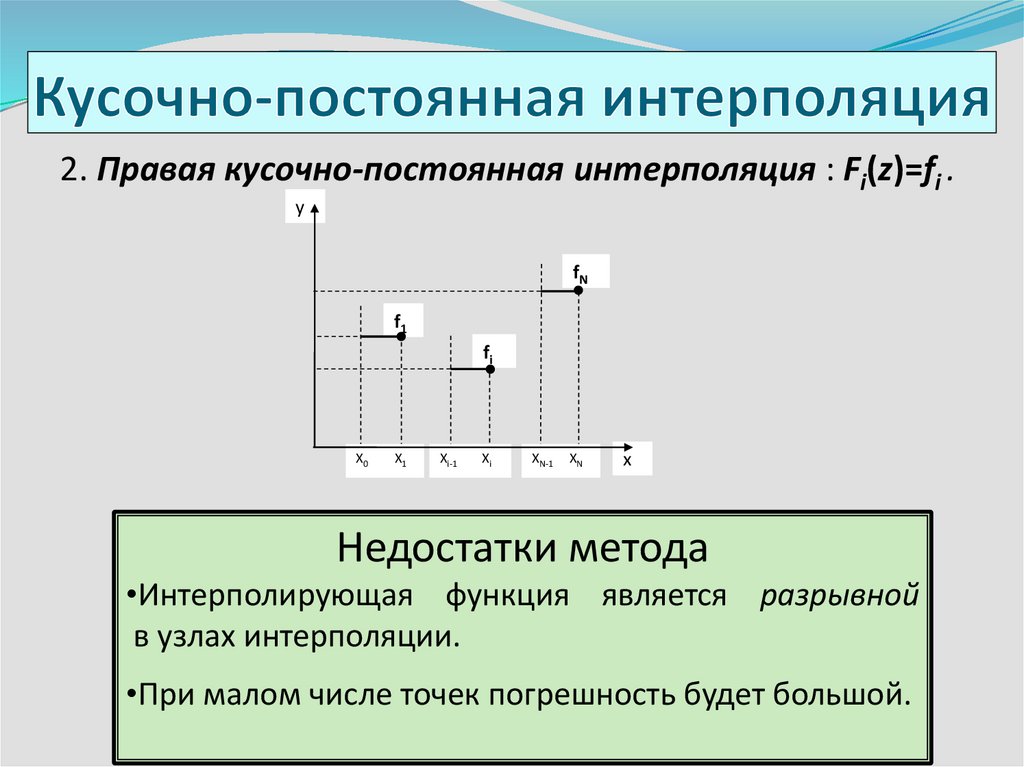
2. Правая кусочно-постоянная интерполяция : Fi(z)=fi .y
fN
f1
fi
X0
X1
Xi-1
Xi
XN-1
XN
x
Недостатки метода
•Интерполирующая функция является разрывной
в узлах интерполяции.
•При малом числе точек погрешность будет большой.
8. Кусочно-постоянная интерполяция (пример)
На интервале [a, b] заданы значения некоторой функции в узлахинтерполяции.
Найти промежуточное значение функции в точке z, используя правую
кусочно-постоянную интерполяцию.
Исходные данные
0
1
2
0.2
0
x f 1
3 2
0.2
0.5
x
3 f 0.5
3.5
0.8
3.5
IKPP ( x f N z)
for i 1 N
if xi 1 z xi
F fi
Решение
m i
break
F
m
0.8
F ( z) IKPP ( x f 3 z)
0.2
1
F ( 1)
0.8
3
F ( 3.2)
9. Кусочно-линейная интерполяция
Накаждом
локальном
отрезке
[xi-1,xi], i=1,…,N
интерполирующая функция заменяется линейной Fi(z)=kiz+li.
Значения коэффициентов ki и li
находятся из
выполнения условий интерполяции на концах отрезка:
F(xi-1)=fi-1;
F(xi)=fi
Составим систему уравнений:
ki xi 1 l i f i 1
ki xi l i f i
Из системы находим коэффициенты:
f i f i 1
ki
; li f i ki xi
xi xi 1
10. Кусочно-линейная интерполяция
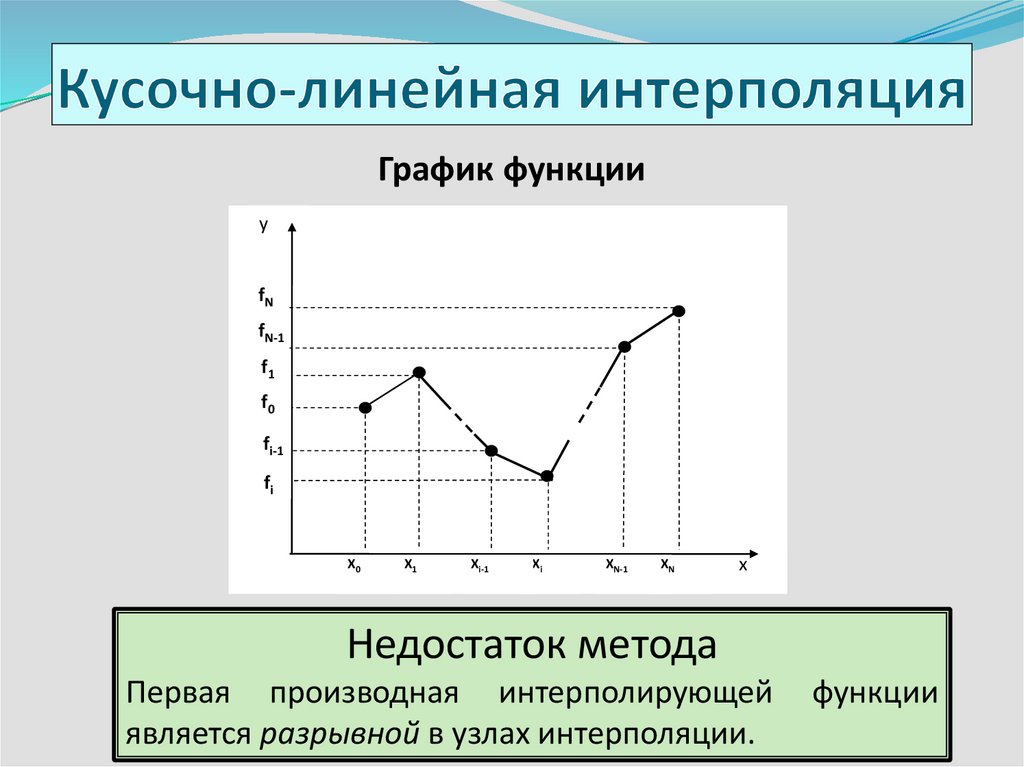
График функцииy
fN
fN-1
f1
f0
fi-1
fi
X0
X1
Xi-1
Xi
XN-1
XN
x
Недостаток метода
Первая производная интерполирующей
является разрывной в узлах интерполяции.
функции
11. Кусочно-линейная интерполяция (пример)
Для функции f(x), заданной таблично, найти значение впромежуточной точке z, используя кусочно-линейную интерполяцию.
Построить график линейной интерполяции в MathCad с помощью
встроенной функции linterp.
0
1
Исходные данные
2
x
3
3.5
0.2
f
0.5
0.8
Решение
IKL( x f N z)
for i 1 N
if x
i 1
F( z) IKL( x f 3 z)
z x
i
i 1
F( 1) 0.4
0.5
f
x x
i
i 1
F( t )
l f k x
i
break
0
0.5
i
F k z l
F
1
i
f f
k
F( t) linterp ( x f t)
F( 1) 0.4
1
0
1
2
x t
3
12. Кубический интерполяционный сплайн
Накаждом
локальном
отрезке
[xi-1,xi],
i=1,…,N
интерполирующая функция описывается кубической параболой:
S i x ai bi x xi ci
x xi 2
di
x xi 3
, i=1,2,…,N
6
Для
определения
4N
неизвестных
коэффициентов
ai, bi, ci, di; i=1,2,…,N используются следующие условия:
Условия интерполяции: Si(xi)=fi; i=1,2,…,N; S1(x0)=f0
Условия непрерывности функции: Si(xi-1)=Si-1(xi-1); i=2,…,N
Условия непрерывности первой производной: Sʹi(xi-1)=Sʹi-1(xi-1);
i=2,…,N
Условия непрерывности второй производной: Sʹʹi(xi-1)=Sʹʹi-1(xi-1);
i=2,…,N
Кубический интерполяционный сплайн имеет достаточно
хорошую точность и простую реализацию.
2
13. Кубический интерполяционный сплайн (пример)
Для построения кубической интерполяции в пакетеMathCad используется встроенная функция: interp(s, x, f, t).
s – вспомогательный вектор коэффициентов, который
вычисляется с помощью функции cspline.
Исходные данные
0
2
x
3
3.5
1
0.2
f
0.5
0.8
s cspline( x f )
S( t ) interp ( s x f t )
1
0.5
Решение
f
S( t )
0
0.5
S( 1) 0.129
1
0
1
2
x t
3
14. ГЛОБАЛЬНАЯ ИНТЕРПОЛЯЦИЯ
Полином ЛагранжаПолином Ньютона
15. Интерполяционный полином Лагранжа
Данный метод основан на построении многочленаN-ой степени, принимающего в узлах интерполяции
xi, i=0,1,…,N заданные значения fi.
Решение ищем в виде полинома Лагранжа
L N z
N
f l z
i i
i 0
где li(z) – базисные полиномы N-ой степени, для
которых выполняется условие:
1, i k
li ( xk )
0, i k
16. Интерполяционный полином Лагранжа
Действительно, если такие базисные полиномыL N z
построены, то полином Лагранжа
будет
удовлетворять условиям интерполяции:
L N xi
N
f l x f l x f l x ... f l x ... f
k k
i
0 0
i
1 1
i
i i
i
N lN
xi
fi
k 0
0
0
1
0
Базисные полиномы N-ой степени для каждого узла
интерполяции строятся следующим образом:
l i z
z x0 z x1 ... z xi-1 z xi+1 ... z x N ;
i=0, 1,..., N
xi x0 xi x1 ... xi xi-1 xi xi+1 ... xi x N
17. Интерполяционный полином Лагранжа
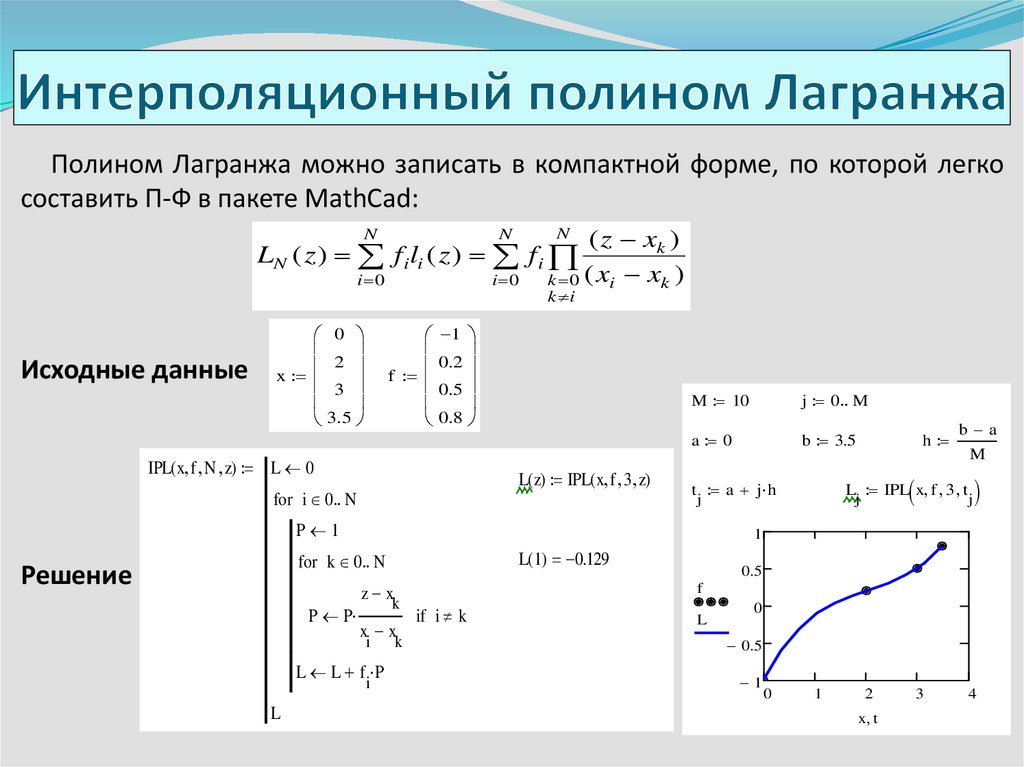
Полином Лагранжа можно записать в компактной форме, по которой легкосоставить П-Ф в пакете MathCad:
( z xk )
k 0 ( xi xk )
N
N
N
i 0
i 0
LN ( z ) f ili ( z ) f i
Исходные данные
0
2
x
3
3.5
k i
1
0.2
f
0.5
0.8
IPL( x f N z) L 0
L( z) IPL( x f 3 z)
for i 0 N
M 10
j 0 M
a 0
b 3.5
t a j h
L( 1) 0.129
z x
P P
j
x x
L L f P
i
0.5
f
k
i
L
j
M
1
for k 0 N
Решение
b a
L IPL x f 3 t
j
P 1
h
k
if i k
L
0
0.5
1
0
1
2
x t
3
4














 Математика
Математика








