Похожие презентации:
Решение заданий ЕГЭ уровня С2 2010 года (2 часть)
1.
МБОУ СОШ №5 – «Школа здоровья и развития»Решение заданий ЕГЭ уровня С2
2010 года
(2 часть)
Учитель математики: Семёнова Елена Юрьевна
2.
Задача №1С2. В правильной треугольной пирамиде сторона
основания равна 4, а боковое ребро равно 3. Найдите
расстояние от стороны основания до противоположного
бокового ребра.
S
E
3
Дано:
SABC – прав. пирамида,
АВ = 4, SA = 3.
Найти: ρ(АС; BS).
С
В
4
O
D Решение:
DЕ – искомое расстояние
А
3.
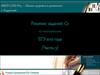
Задача №2С2. В основании треугольной пирамиды SABC лежит
прямоугольный треугольник с прямым углом при
вершине С, гипотенузой АВ = 13 и катетом ВС = 5.
Найдите расстояние между ребрами AS и ВС, если длина
высоты SB равна 9.
S Дано:
SABC – пирамида,
∆ABC – п/у, С = 90 ,
SB (ABC)
K
9 ВC = 5, SB = 9, AB = 13.
Найти: ρ(АS; BС).
D 13
В
5
А
С
Решение:
ВK – искомое расстояние
4.
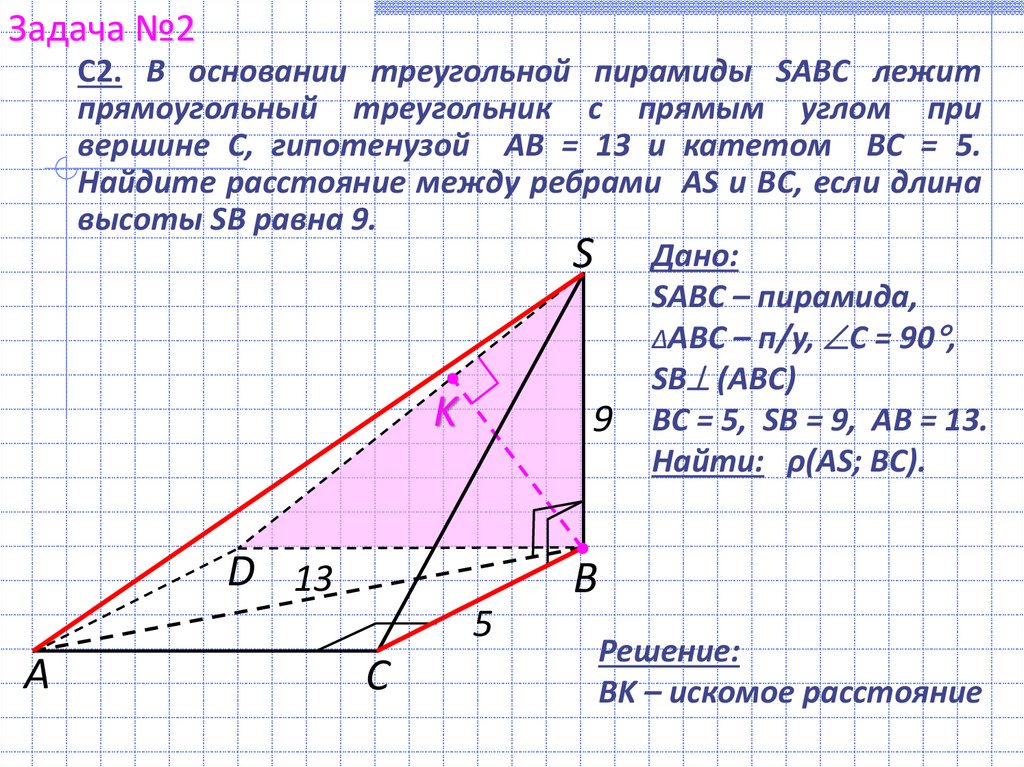
Задача №3 С2. В основании треугольной пирамиды SABCS
лежит прямоугольный треугольник с прямым
углом при вершине В и катетом АВ = 6.
Найдите расстояние между ребрами SA и ВС,
если вершина пирамиды проектируется в
середину ребра АВ, а высота пирамиды равна 4.
Дано:
SABC – пирамида,
∆ABC – п/у, B = 90 ,
SD (ABC), AD = DB,
AВ = 6, SD = 4.
Найти: ρ(AS; BС).
E
4
А
6
С
D
Решение:
ВЕ – искомое расстояние
В
5.
Задача №4S
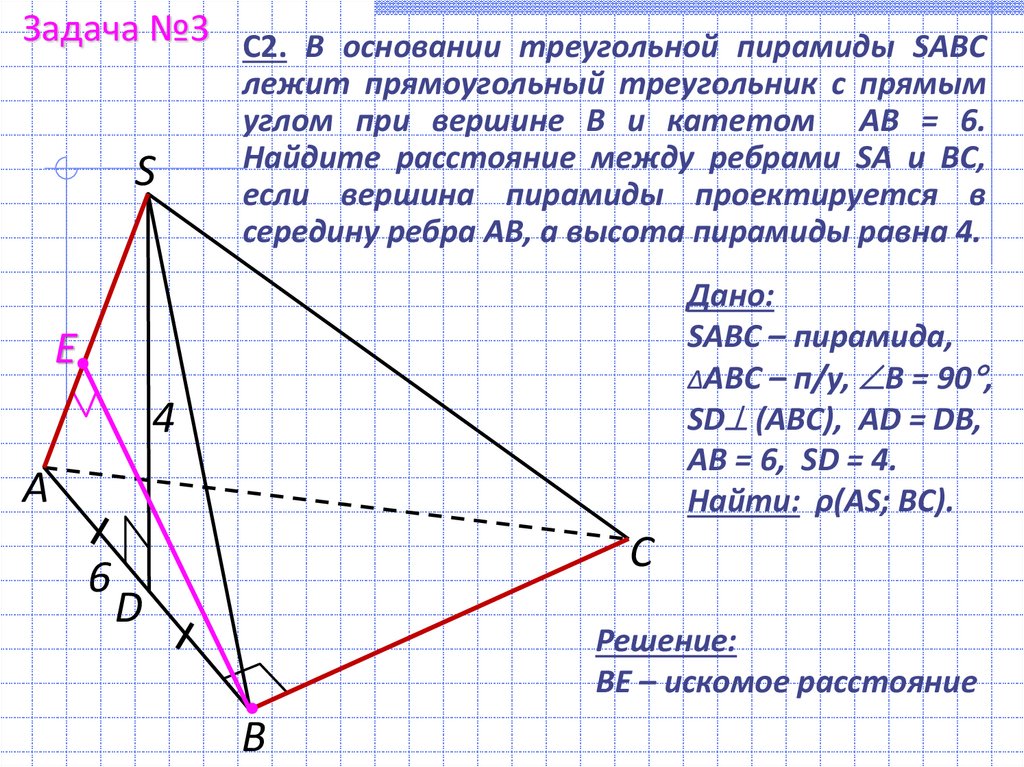
С2. В основании треугольной пирамиды SABC
лежит
прямоугольный
треугольник
с
катетом ВС = 3 и гипотенузой АС = 5.
Расстояние между ребрами SA и ВС равно 3.
Найдите длину ребра SA, если вершина
пирамиды проектируется в середину ребра АВ.
E
А
5
3
С
D
3
В
Дано:
SABC – пирамида,
∆ABC – п/у, B = 90 ,
SD (ABC), AD = DB,
AC = 5, BC = 3,
ρ(BС; AS) = 3.
Найти: SA.
6.
Задача №5С2. Дан куб ABCDA1B1C1D1. Найдите расстояние от
вершины А1 до плоскости AB1D1, если ребро куба
равно 3.
D1
3
С1
В1
3
Н
А1
S
D
А
Дано:
ABCDA1B1C1D1 – куб,
AB = 3,
(AB1D1) – секущая
плоскость.
Найти: ρ(A1; AB1D1).
С
В
Решение:
A1S – искомое расстояние
7.
Задача №5.1В1
С2. Дан куб ABCDA1B1C1D1. Точки M, N, P, K –
соответственно середины ребер A1B1, A1D1, BC, DC.
Найдите расстояние между плоскости AMN и С1РК,
если ребро куба равно 6.
Дано:
А1
ABCDA1B1C1D1 – куб,
N
D1
AB = 6,
M
(AMN), (PKC1) –
секущие плоскости.
С1
Найти:
6
S
ρ((AMN), (PKC1)).
6
В
А
P
D
R
K
С
Решение:
RS – искомое расстояние
8.
Задача №5.2А1
С2. Дан куб ABCDA1B1C1D1. Точки M, N, P, K –
соответственно середины ребер A1B1, A1D1, BC, DC.
Найдите расстояние между плоскости AMN и С1РК,
если ребро куба равно 6.
Дано:
С1
D1
ABCDA1B1C1D1 – куб,
6
AB = 6,
N
(AMN), (PKC1) –
M
секущие плоскости.
В1
Найти:
6
S
ρ((AMN), (PKC1)).
K
D
А
R
В
С
P
Решение:
RS – искомое расстояние
9.
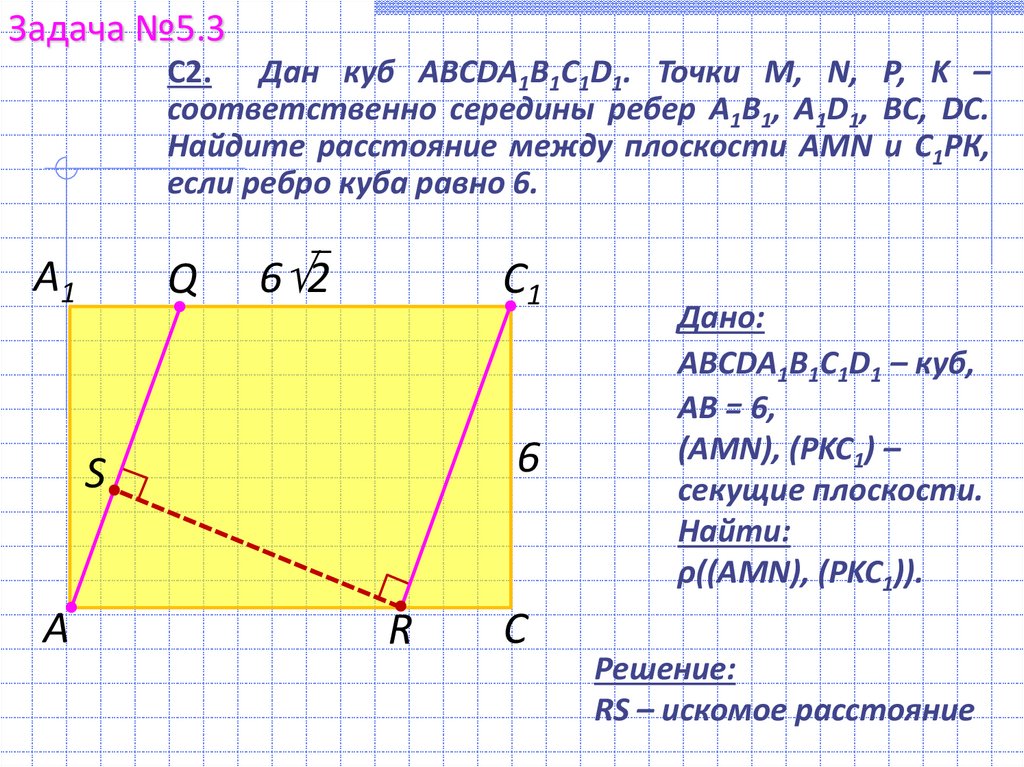
Задача №5.3С2. Дан куб ABCDA1B1C1D1. Точки M, N, P, K –
соответственно середины ребер A1B1, A1D1, BC, DC.
Найдите расстояние между плоскости AMN и С1РК,
если ребро куба равно 6.
А1
Q
6 2
С1
6
S
А
R
С
Дано:
ABCDA1B1C1D1 – куб,
AB = 6,
(AMN), (PKC1) –
секущие плоскости.
Найти:
ρ((AMN), (PKC1)).
Решение:
RS – искомое расстояние
10.
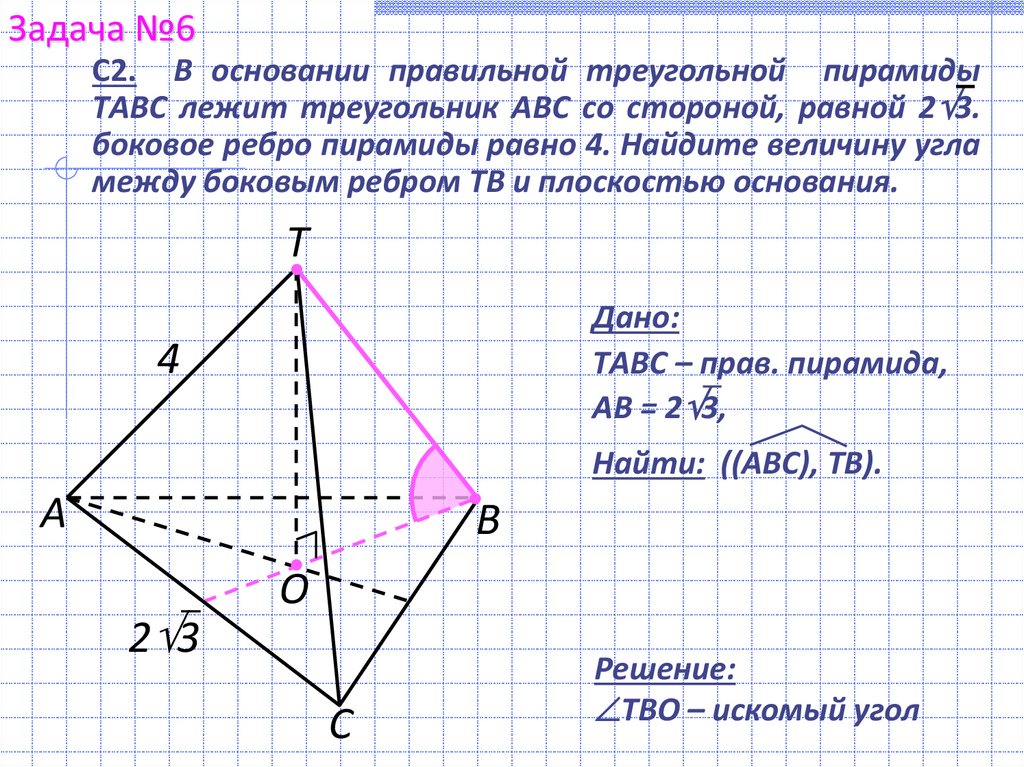
Задача №6С2. В основании правильной треугольной пирамиды
ТABC лежит треугольник АВС со стороной, равной 2 3.
боковое ребро пирамиды равно 4. Найдите величину угла
между боковым ребром ТВ и плоскостью основания.
Т
Дано:
ТABC – прав. пирамида,
AB = 2 3,
4
Найти: ((AВС), ТВ).
А
В
2 3
О
С
Решение:
ТВО – искомый угол
11.
Задача №7.1С2.
В кубе ABCDA1B1C1D1 точки N, K, P –
соответственно середины ребер A1B1, В1С1, АD.
Найдите тангенс угла наклона ребра АВ к
плоскости NКР.
Дано:
ABCDA1B1C1D1 – куб,
1
1
A1N = NB1, B1K = KC1,
AP = PD.
Найти: (AB, (NKP)).
В
N
А1
K
С
D1
R
Q
L
В
T
А
P
D
S
С
12.
Задача №7.2С2.
В кубе ABCDA1B1C1D1 точки N, K, P –
соответственно середины ребер A1B1, В1С1, АD.
Найдите тангенс угла наклона ребра АВ к
плоскости NКР.
Дано:
ABCDA1B1C1D1 – куб,
A1N = NB1, B1K = KC1,
AP = PD.
Найти: (AB, (NKP)).
D1
С1
K
N
А1
В1
G
R
Q
D
T
Решение:
GTB – искомый угол
S
P
А
В
С







 Математика
Математика