Расчет фермы 2020

1.

Расчет фермы
2020

2. Ферма

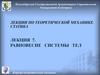
Ферма – это геометрически неизменяемая система, состоящая из прямых
стержней, соединенных по концам жестко или шарнирно.
Замена жестких узлов шарнирами превращает их в шарнирную ферму. При
узловой нагрузке стержни шарнирной фермы работают на растяжение или
сжатие.
2

3. Ферма

Фермы широко применяются для перекрытия больших пролетов в конструкциях
мостов, кранов, стропил и т.д. Это обусловлено тем, что при малом расходе материалов
и малом собственном весе фермы способны воспринимать значительные внешние
нагрузки. Кроме того, расчет стержневых шарнирных ферм производится достаточно
просто.
1
3
4
А
•
5
•
В
2
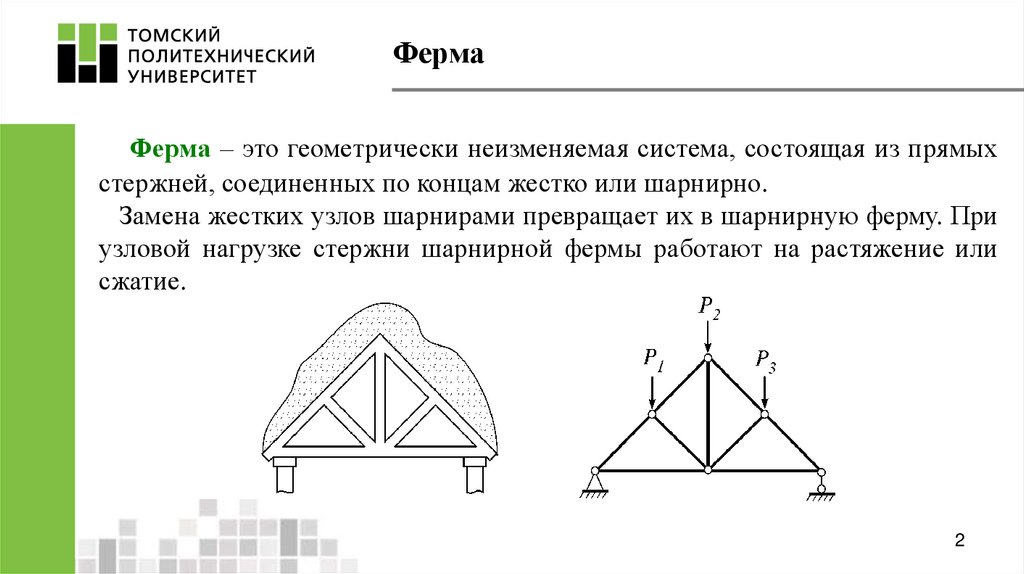
Элементы фермы и генеральные размеры
1 – верхний пояс,
2 – нижний пояс,
3 – узел фермы,
4 – раскос,
5 – стойка,
А, В – опорные узлы,
АВ – пролет фермы.
3

4. Ферма

Разнообразие областей применения и конструктивных решений ферм позволяет
классифицировать их по различным признакам:
по назначению – фермы мостов, перекрытий (стропильные и подстропильные),
транспортных эстакад, грузоподъемных кранов, гидротехнических затворов и других
сооружений.
1.
5.
по очертанию поясов:
1- с параллельными поясами
2.
6.
2-трапецеидальная
3- арочные
4-треугольные
3.
5-с треугольной решеткой
7.
6- с треугольной решеткой и
дополнительными стойками
4.
7- с раскосной решеткой.
4

5. Ферма

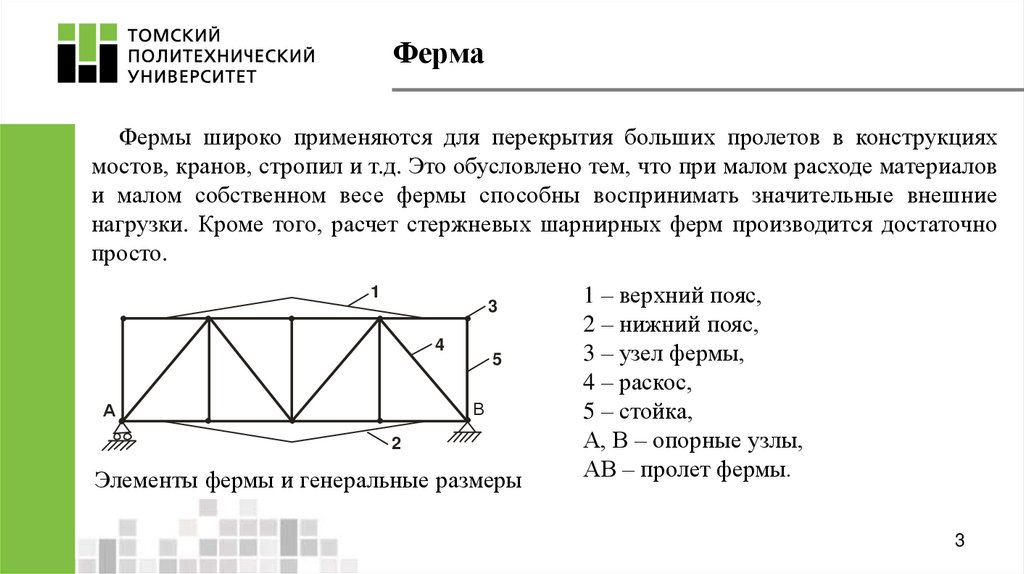
Очертание поясов зависит главным образом от назначения фермы и принятой
конструктивной схемы сооружения по системе решетки:
Решетки специальных типов:
1- со шпренгельной решеткой
2- крестовая
1.
3- ромбическая
4- полураскосная.
2.
3.
4.
5

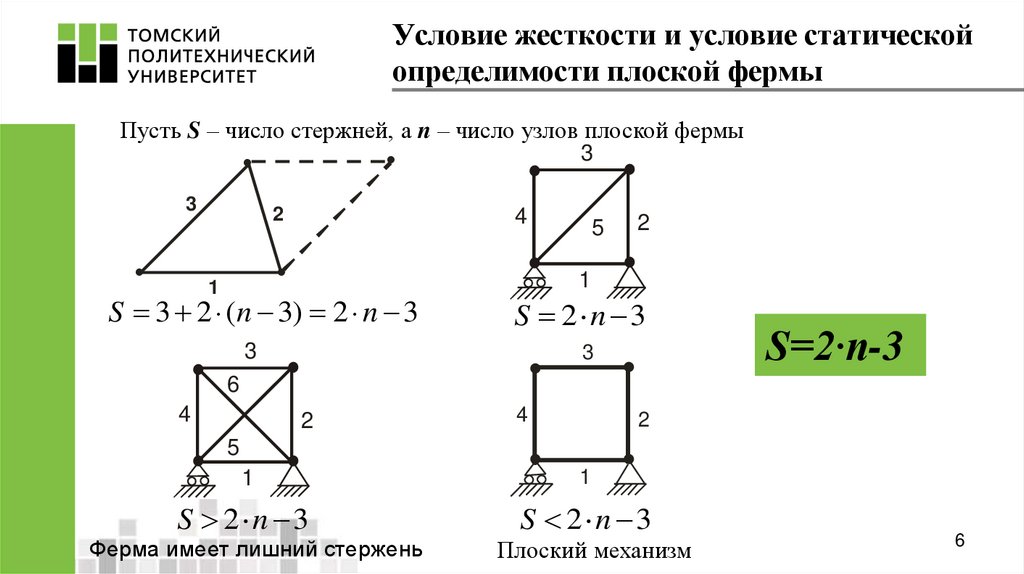
6. Условие жесткости и условие статической определимости плоской фермы

Пусть S – число стержней, а n – число узлов плоской фермы
3
1
2
4
•
S 3 2 (n 3) 2 n 3
• 6
3
4
5
1
2
S 2 n 3
2
3
3
4
S=2·n-3
2
•• 5 1
•
S 2 n 3
S 2 n 3
Ферма имеет лишний стержень
Плоский механизм
1
6

7. Расчет фермы

Вследствие принятой расчетной схемы в стержнях фермы моменты и поперечные
силы отсутствуют, действуют только продольные усилия.
Положительное (растягивающее) усилие Nij в стержне фермы между узлами i и j
следует направить в сторону от шарнира:
При расчете простых ферм используются методы:
вырезания узлов,
сквозных сечений,
совместных сечений,
замены стержней и др.
7

8. Метод вырезания узлов

Метод основан на последовательном вырезании и рассмотрении равновесия узлов
фермы.
Сущность метода:
• вырезается узел, в котором не более двух неизвестных; составляются уравнения
равновесия ΣX=0 и ΣY=0;
• из них определяются два неизвестных продольных усилия. После этого можно
вырезать следующий узел и продолжить расчет.
У метода вырезания узлов есть один недостаток: ошибка (неточность), допущенная
при расчете одного узла, влияет на последующие вычисления. Поэтому полученные
результаты надо контролировать.
8

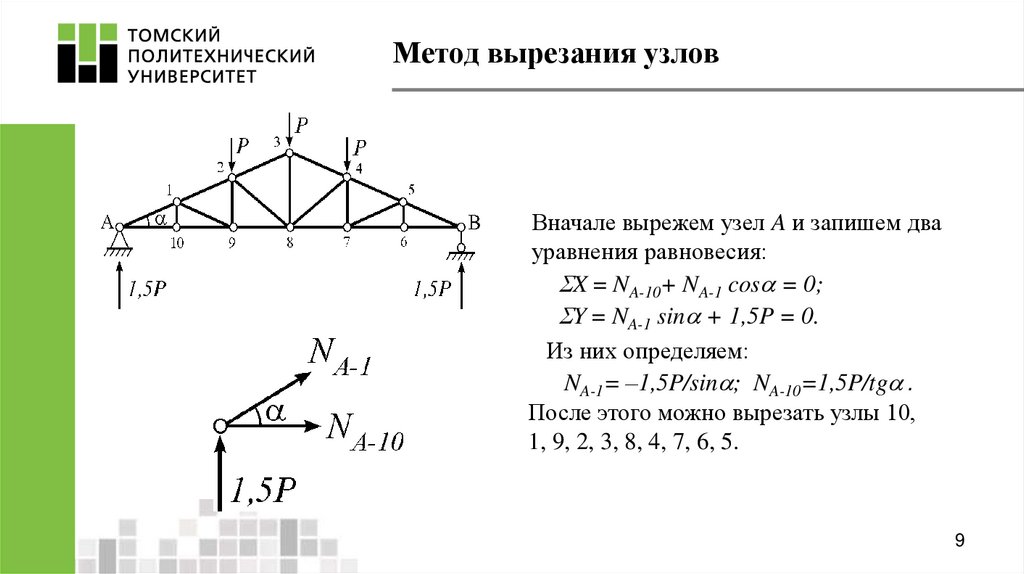
9. Метод вырезания узлов

Вначале вырежем узел A и запишем два
уравнения равновесия:
X = NA-10+ NA-1 cos = 0;
Y = NA-1 sin + 1,5P = 0.
Из них определяем:
NA-1= –1,5P/sin ; NA-10=1,5P/tg .
После этого можно вырезать узлы 10,
1, 9, 2, 3, 8, 4, 7, 6, 5.
9

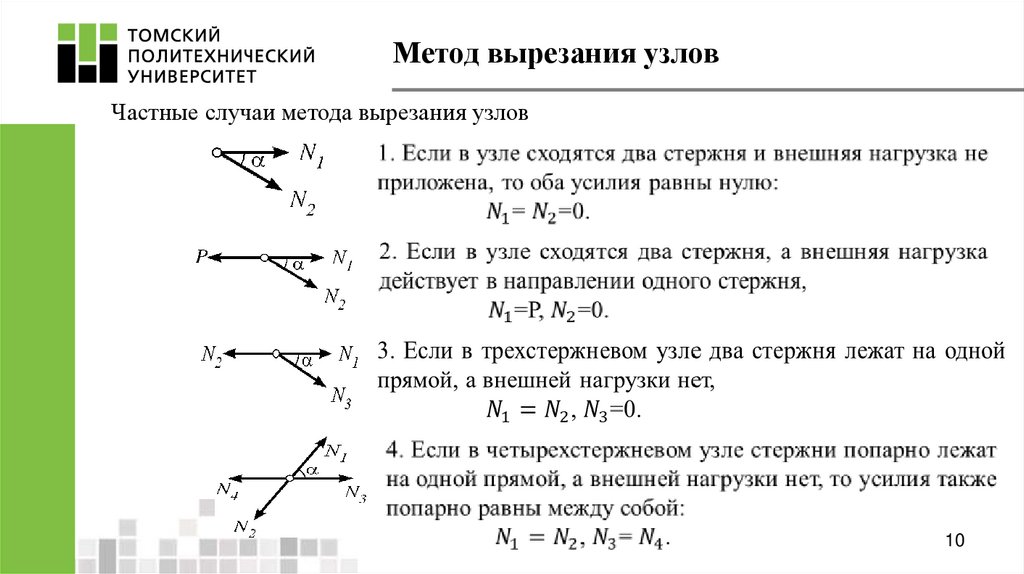
10. Метод вырезания узлов

Частные случаи метода вырезания узлов
10

11. Метод вырезания узлов

Последовательность применения метода:
1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции.
2. Выбираем узел фермы в котором сходятся два стержня с неизвестными усилиями.
3. Отбрасываем стержни, заменяя их действие на узел реакциями. Реакции стержней
направляем по осям стержней от узла. Это соответствует предположению о том, что все
стержни растянуты.
4. Составляем два уравнения равновесия для плоской системы сходящихся сил, действующих на выбранный узел.
5. Решая составленные уравнения, находим усилия в стержнях. Если усилия в стержнях получились со знаком «-» то это означает, что соответствующие стержни сжаты.
6. Последовательно вырезаем узлы фермы так, чтобы в двух уравнениях равновесия для
каждого из узлов было не более двух неизвестных усилий.
7. Вырезание последнего узла может служить для контроля правильности расчета.
11

12. Метод сквозных сечений (метод Риттера)

Позволяет определять усилие в стержне лишь из одного уравнения.
Сущность метода:
• поперек фермы проводится такое сквозное сечение, чтобы появилось не более трех
неизвестных усилий;
• в точке пересечения направлений двух из них составляется уравнение момента;
• из этого уравнения определяется третье усилие.
Точка составления уравнения момента называется моментной точкой. Когда два
стержня параллельны, моментной точки нет. В таком случае надо составлять
уравнение проекции на ось, перпендикулярную этим параллельным стержням.
У метода сквозных сечений есть один недостаток: иногда не удается провести
сквозное сечение так, чтобы появились только три неизвестные.
В таком случае одно из усилий необходимо определить заранее.
12

13. Метод сквозных сечений (метод Риттера)

Последовательность применения метода:
1. Выбираем в качестве объекта равновесия ферму в целом и определяем опорные реакции.
2. Проводим сквозное сечение, разделяющее ферму на две отдельные части так, чтобы в
сечение попадало не более трех стержней, в одном из которых требуется найти усилие.
3. Выбираем в качестве объекта равновесия одну часть фермы, как правило ту, на которую
действует меньшее число сил, и отбрасываем другую часть фермы.
4. Действие отброшенной части на оставшуюся заменяем реакциями стержней, попавших
в сечение, направляя их по осям стержней в сторону отброшенной части. Это соответствует
предположению о том, что все стержни растянуты.
5. Для оставшейся части фермы находим точки Риттера – точки, в которых попарно
пересекаются линии действия усилий в рассеченных стержнях. В общем случае таких точек
будет три.
13

14. Метод сквозных сечений (метод Риттера)

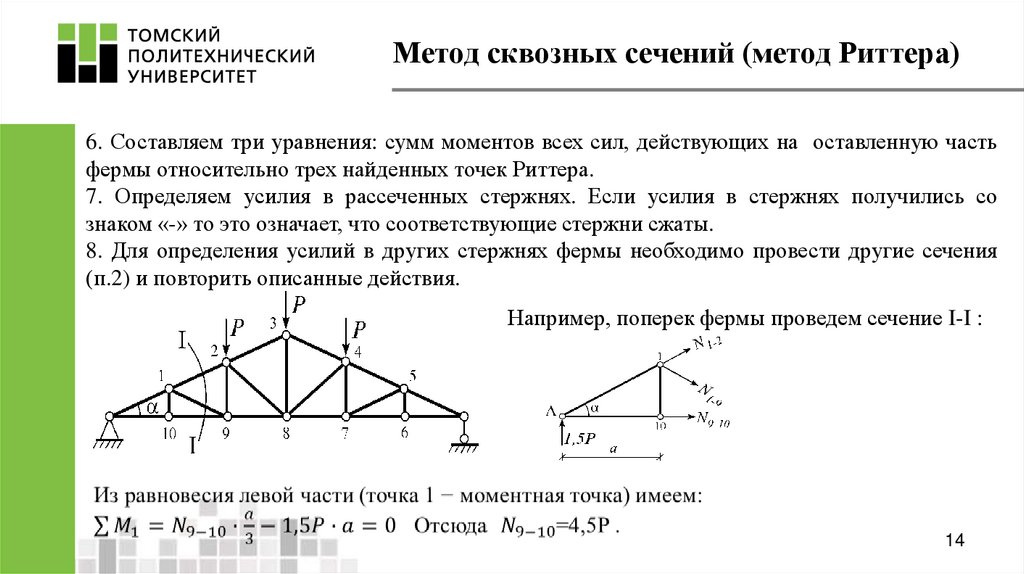
6. Составляем три уравнения: сумм моментов всех сил, действующих на оставленную часть
фермы относительно трех найденных точек Риттера.
7. Определяем усилия в рассеченных стержнях. Если усилия в стержнях получились со
знаком «-» то это означает, что соответствующие стержни сжаты.
8. Для определения усилий в других стержнях фермы необходимо провести другие сечения
(п.2) и повторить описанные действия.
Например, поперек фермы проведем сечение I-I :
14

15. Пример решения методом вырезания узлов

Условие: Ферма из стальных стержней нагружена сосредоточенными силами.
Требуется:
1.Определить опорные реакции.
2.Определить усилия во всех стержнях фермы, методом вырезания узлов.
Дано: по своему индивидуальному шифру выбираем исходные данные из таблицы
и расчетную схему фермы.
Р1/Р2=300/100, кН
P2
P1
P3
2
1
α
L
3
L
P4
Р3/Р4=380/70, кН
α =40⁰
L=3,5 м
Запись данных Р1/Р2 = 300/100 означает, что Р1
= 300кН, а Р2 = 100кН.
Усилия, равные нулю, на расчетной схеме не
15
показываем.

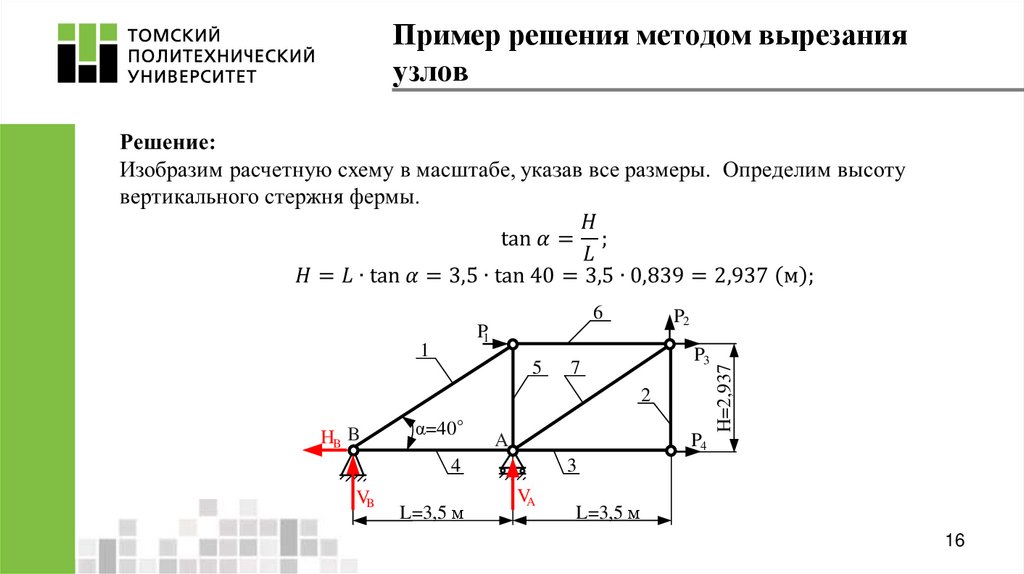
16. Пример решения методом вырезания узлов

6
1
5
P3
7
2
HB B
α=40°
A
P4
3
4
VB
L=3,5 м
H=2,937
P2
P1
VA
L=3,5 м
16

17. Пример решения методом вырезания узлов

17

18. Пример решения методом вырезания узлов

6
1
5
P3
7
2
HB B
α=40°
A
P4
3
4
VB
L=3,5 м
H=2,937
P2
P1
VA
L=3,5 м
18

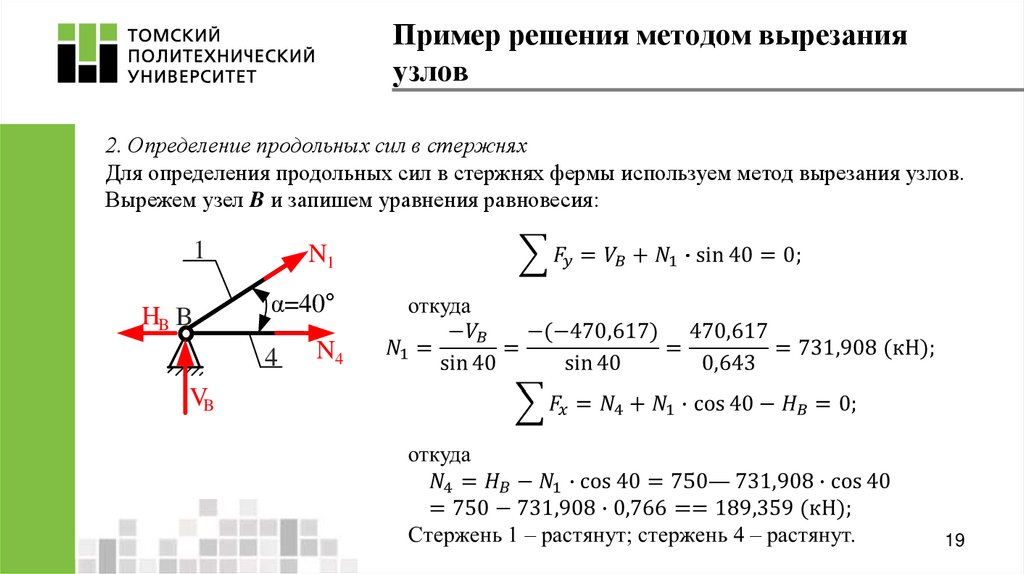
19. Пример решения методом вырезания узлов

2. Определение продольных сил в стержнях
Для определения продольных сил в стержнях фермы используем метод вырезания узлов.
Вырежем узел B и запишем уравнения равновесия:
1
HB B
N1
α=40°
4
N4
VB
19

20. Пример решения методом вырезания узлов

Вырежем узел К и запишем уравнения равновесия:
6
1 P1
N1
50°
K
5
N6
N5
20

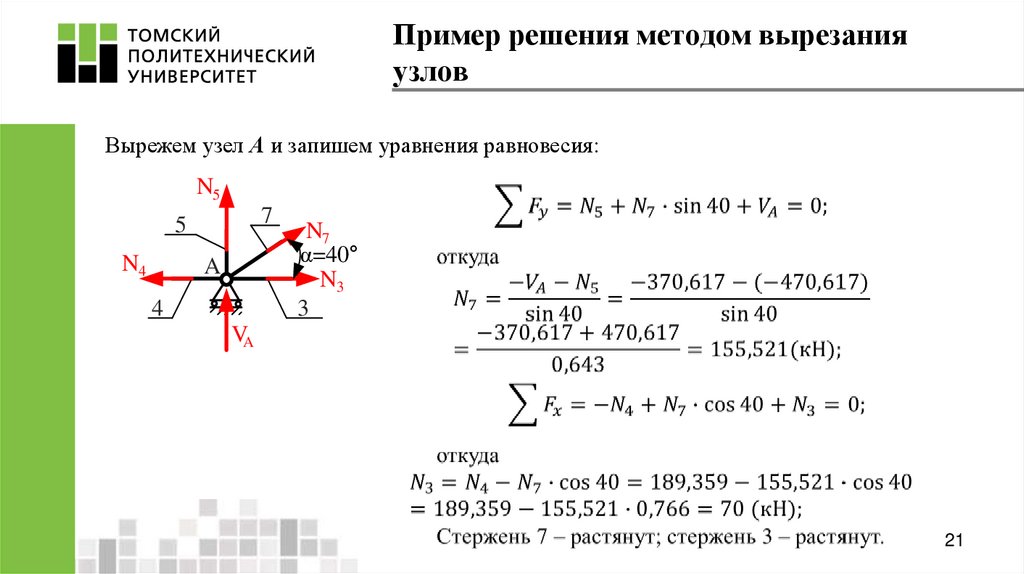
21. Пример решения методом вырезания узлов

Вырежем узел А и запишем уравнения равновесия:
N5
7
5
N4
A
4
N7
α=40°
N3
3
VA
21

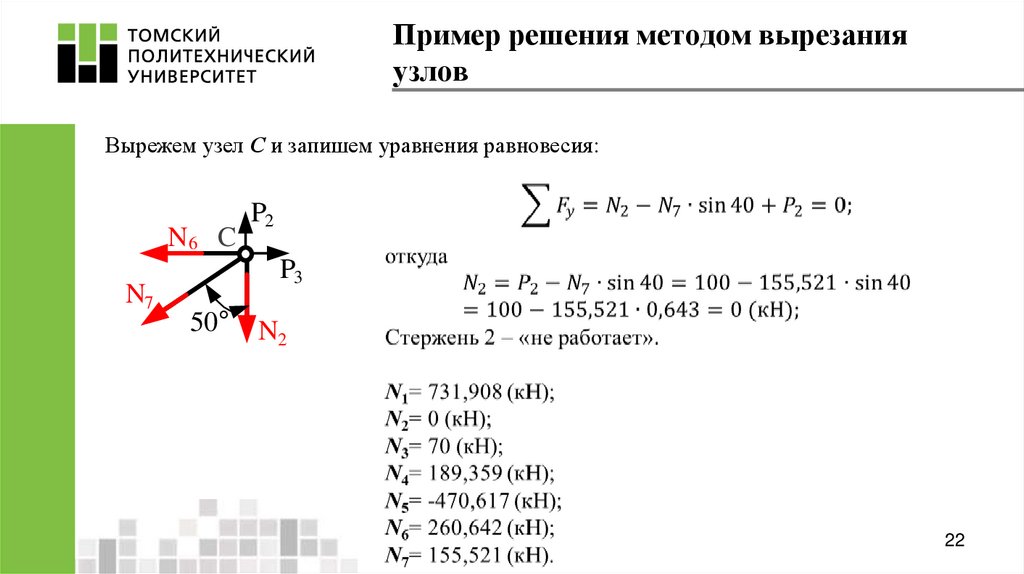
22. Пример решения методом вырезания узлов

Вырежем узел С и запишем уравнения равновесия:
N6 C
N7
P2
P3
50°
N2
22