Геометрические характеристики плоских сечений. Лекция 9

1.

ГЕОМЕТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
Лекция 9

2.

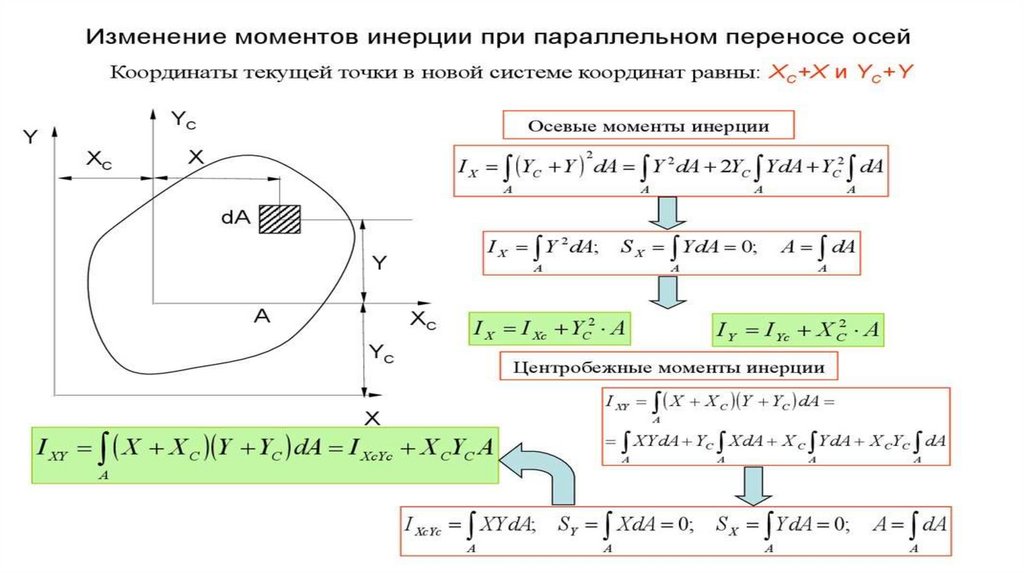
Статический момент относительно центральной оси равен нулю, поскольку равно нулю расстояние от центра
тяжести до центральной оси.

3.

4.

5.

6.

7.

Моменты инерции треугольника
Определим момент инерции треугольника относительно
оси х1, проходящей через его основание (рис). С этой целью
выделим на текущем расстоянии у от этой оси
элементарную площадку шириной dy и площадью dA. Эта
площадка имеет форму трапеции со средней линией by.
Часть треугольника, расположенная выше текущей
координаты у, подобна самому треугольнику.
На основании этого подобия можно записать пропорцию:
by
b
bh 3
J x1
12
h y
h
момент инерции треугольника относительно оси,
проходящей через его основание
h y
by b
h

8.

3
bh
Jx
36
bh
Jx
4
момент инерции треугольника относительно
оси, проходящей через центр его тяжести
параллельно основанию
3
момент инерции треугольника относительно
оси, проходящей через его вершину
параллельно основанию

9.

10.

11.

12.

13.

Пример 1. Определить моменты
инерции ромба относительно осей,
проходящих через его диагонали (рис.
9.12). Размеры диагоналей: h=120 мм,
b=64 мм.

14.

Пример 2. Определить моменты
инерции прямоугольного сечения с
отверстием относительно
центральных осей хС и уС (рис. 9.13).
Размеры прямоугольника: b=74 мм;
h=108 мм. Диаметр отверстия d=56
мм. Расстояние от основания фигуры
до центра отверстия е=68 мм.

15.

Пример 3. Определить моменты
инерции
равнобочной
трапеции
относительно центральных осей хС и
уС (рис. 9.14). Большое основание
трапеции В=54 мм, малое основание
трапеции b=27 мм, высота трапеции
h=50 мм.