Геометрические характеристики плоских сечений

1.

ЛЕКЦИЯ №4
1
ГЕОМЕТРИЧЕСКИЕ
ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ

2.

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
2
Сопротивление бруса различным видам деформаций часто зависит не
только от его материала и размеров, но также от формы поперечных
сечений и их расположения относительно направления действующих
нагрузок.
Площадь поперечного сечения бруса является геометрической
характеристикой его прочности и жесткости лишь при равномерном
распределении напряжений по поперечному сечению.
При неравномерном распределении напряжений, имеющим место при
работе бруса на кручение (изгиб) его прочность и жесткость зависят от
более сложной геометрической характеристики – момента инерции.

3.

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
3
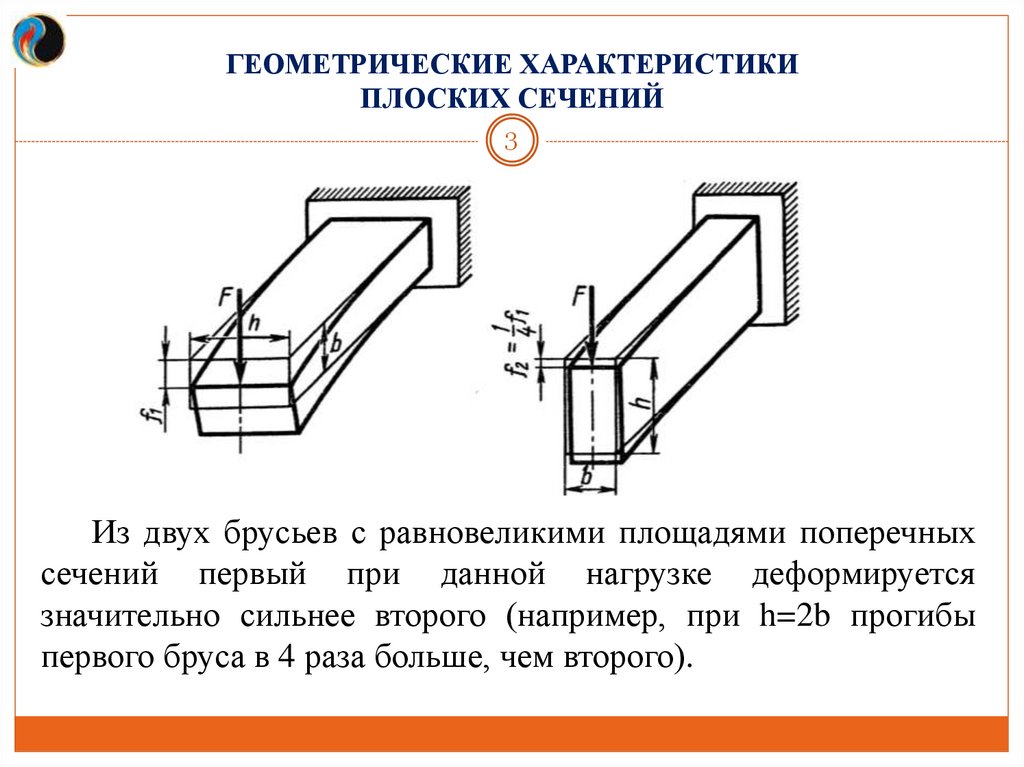
Из двух брусьев с равновеликими площадями поперечных
сечений первый при данной нагрузке деформируется
значительно сильнее второго (например, при h=2b прогибы
первого бруса в 4 раза больше, чем второго).

4.

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ
ПЛОСКИХ СЕЧЕНИЙ
4
Эта лекция посвящена ознакомлению со свойствами и методами
вычисления специальных геометрических характеристик плоских сечений,
используемых при расчетах на изгиб, на изгиб с растяжением и в ряде
других случаев.
Основными
геометрическими
характеристиками
являются:
статические моменты, моменты инерции, моменты сопротивления,
радиусы инерции.
Статическим моментом плоского сечения относительно оси
называется взятая по всей площади сечения сумма произведений площадей
элементарных площадок на их расстояние до этой оси.
S x ydF
F
S y xdF
F

5.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
5
Введем декартову прямоугольную систему
координат XOY.
Рассмотрим в
плоскости
координат
произвольное сечение (замкнутую область)
площадью F.
C – центр тяжести сечения
Выделим элементарную площадку dF.
- полярный радиус.
y
y
yc
F
dF
C
0
x
x
xc
Статическими моментами сечения относительно осей у и х называются
интегралы вида:
S x ydF
F
S y xdF
F
Статические моменты сложного сечения можно определить как:
n
S x S xi
i 1
n
S у S уi
i 1
где: i = 1 n – число простых сечений;
Sxi, Syi - статические моменты простых сечений

6.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
6
Рассмотрим две пары параллельных
осей: х1, х2 и у1, у2.
Поместим в них тело площадью F с
элементарной площадкой dF.
Пусть расстояние между осями х1 и х2
равно b; расстояние между осями у1 и у2
равно a, тогда:
x2 x1 a
y2
y1
у2
у1
F
dF
О2
b a
О1
y2 y1 b
Полагаем, что х1, у1 и Sx1, Sy1 заданы. Найдем Sx2, Sy2
х2
x1
x2
x1

7.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
7
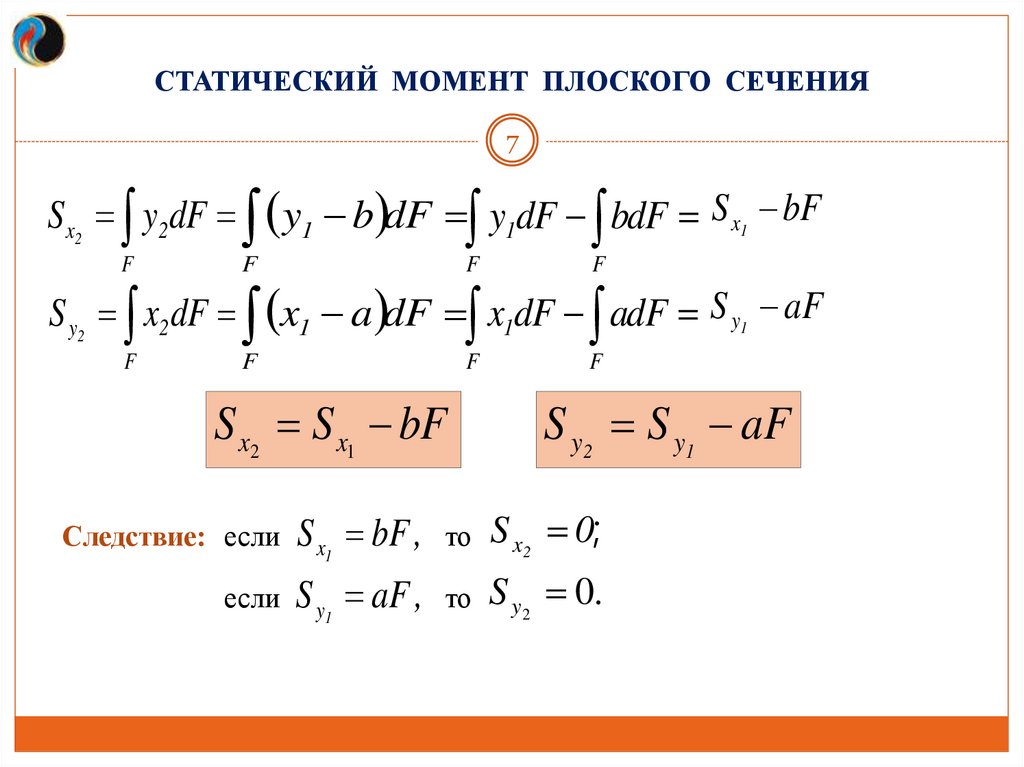
S x2 y2 dF y1 b dF y1dF bdF S x1 bF
F
F
F
F
F
F
F
F
S y2 x2 dF x1 a dF x1dF adF S y1 aF
S x2 S x1 bF
S y2 S y1 aF
bF , то S x2 0;
если S y aF , то S y2 0.
1
Следствие: если S x
1

8.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
8
Оси, относительно которых статические моменты равны нулю,
называются центральными.
Точка пересечения центральных осей х и у (точка С с координатами хc и yc)
называется центром тяжести сечения.
xdF
Sy F
xc
F
F
ydF
Sx F
yc
F
F
Если оси х и у проходят через центр тяжести сечения, хс = 0 и ус = 0,
следовательно: S y F 0 , S y xc F 0.
x
c
Статический момент может принимать положительные,
отрицательные и равные нулю значения.
Размерность: [м3]

9.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
9
Приложение
Декартова система координат (х, у)
y
dF
dF = dxdy
dy
y
x
x
у
2
0
x
dS
dF
d
dr
r
dF = r·dr·d
x
dS
d
R
О
y
y
dх
0
Полярная система координат (r, )
x
Переход к декартовой системе координат:
х r cos
S = 2πR - длина окружности;
dS – длина дуги окружности.
y r sin
2
d
dS Rd
2 R
dS

10.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
10
Пример
Определить, на каком расстоянии от основания находится центр тяжести
треугольника произвольной формы
у
Площадь треугольника: F 1 2 bh
h
полагаем, что: dF b y dy
dу
dF
у
C
О
b(y)
b
x
Из подобия двух треугольников следует:
b y h y
b h y
b y
b
h
h
Определим статический момент относительно оси x:
b h y
yb
by
by
bh 2 bh 3 bh 2
S x yb y dy y
dy ybdy
dy
h
h
2 0 h3 0
2
h3
6
F
0
0
0
2
h
S
bh
2 h
Определим центр тяжести
x
y
Ответ: c
yc
3
треугольника относительно оси x:
F 6 bh 3
h
h
h
2
2 h
3 h

11.

СТАТИЧЕСКИЙ МОМЕНТ ПЛОСКОГО СЕЧЕНИЯ
11
Пример
Определить центр тяжести полукруга
Площадь полукруга:
у
2
Определим статический момент относительно оси x:
R
R
0
0
S x ydF r sin rdrd sin d r 2 dr
C
О
F
R 2
r
F
x
F
3 R
r
R3 2 3
cos
cos cos 0 R
3 3
0 3 0
Определим центр тяжести полукруга:
S x 2R3 2
yc
0,424 R
2
F
3 R
Ответ:
yc 0,424 R

12.

МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЯ
12
Осевым (экваториальным) моментом инерции плоского
сечения относительно данной оси называется взятая по всей
площади сечения сумма произведений площадей элементарных
площадок на квадраты их расстояний до этой оси.
J x y dF
2
F
J y x 2 dF
F
Осевые моменты инерции могут принимать положительные
и равные нулю значения.
Размерность: [м4].

13.

МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЯ
13
Если сечение площадью F можно представить в виде суммы нескольких замкнутых
областей F = F1 + F2 + … + Fn, то по аналогии со статическими моментами:
n
S x ydF1 ydF2
ydFn ydFi
S y xdF1 xdF2
xdFn xdFi
F1
F2
F1
F2
i 1 Fi
n
Fn
i 1 Fi
Fn
осевые моменты инерции можно представить в виде:
J x y 2 dF1 y 2 dF2
F1
F2
J y x dF1 x dF2
2
F1
2
F2
n
y 2 dFn y 2 dFi
i 1 Fi
Fn
n
x dFn x dFi
2
Fn
2
i 1 Fi

14.

МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЯ
14
Сумма осевых моментов инерции относительно двух взаимно
перпендикулярных осей равна полярному моменту инерции
относительно точки пересечения этих осей (начала координат)
J x 2 y 2 dF 2 dF
F
F
Где - полярный радиус
Очевидно, что
J x y dF x dF y dF J y J x
2
2
2
2
F
F
F
Полярный момент инерции может принимать положительные или равные
нулю значения.
Размерность: [м4]

15.

МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЯ
15
Центробежный момент инерции представляет собой взятую по всей
площади сечения сумму произведений площадей элементарных площадок
на произведение их расстояний до двух данных взаимно перпендикулярных
осей.
J xу хydF
F
Центробежный момент инерции может принимать положительные,
отрицательные или равные нулю значения.
Размерность: [м4]

16.

ГЛАВНЫЕ ОСИ ИНЕРЦИИ СЕЧЕНИЯ
16
Главными осями инерции сечения называются две
взаимно перпендикулярные оси, относительно которых
центробежный момент инерции Jxy = 0, а осевые моменты
инерции Jx, Jy принимают экстремальные значения.
Если одна из взаимно перпендикулярных осей является
осью симметрии сечения, то Jxy = 0.
Главные оси инерции, проходящие через центр тяжести
сечения, называются главными центральными осями
инерции сечения.

17.

ТЕОРЕМА ШТЕЙНЕРА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ
y1
b
17
y
F
у
dF
x
С
х
a
x1
О1
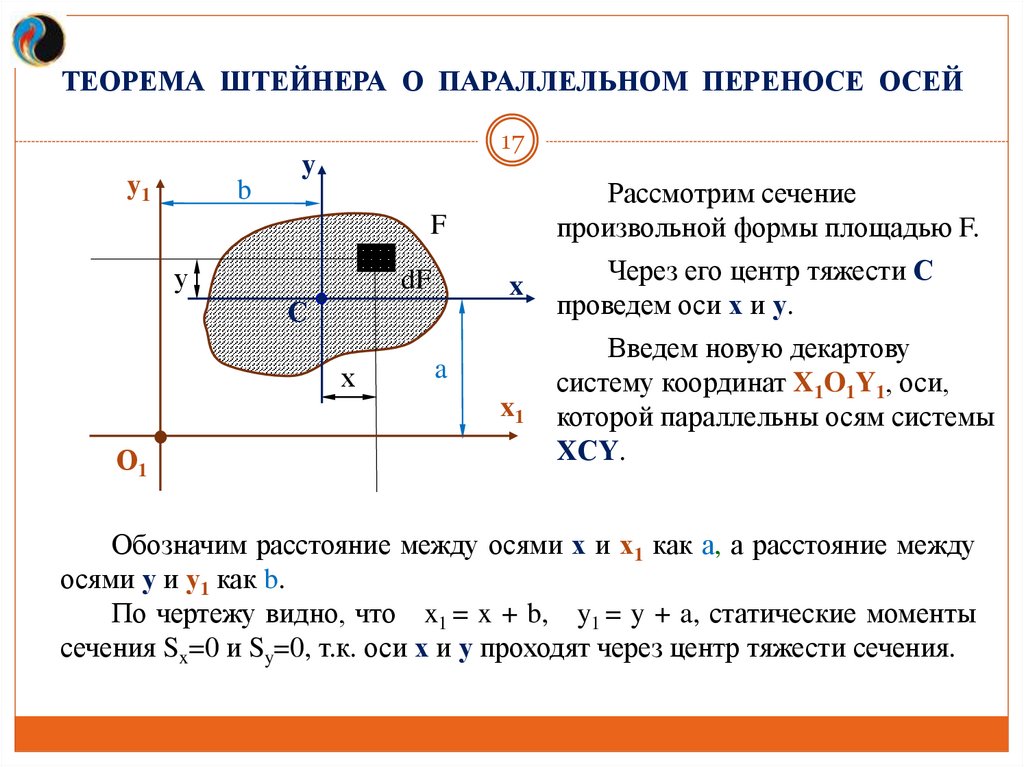
Рассмотрим сечение
произвольной формы площадью F.
Через его центр тяжести С
проведем оси х и у.
Введем новую декартову
систему координат X1O1Y1, оси,
которой параллельны осям системы
XСY.
Обозначим расстояние между осями х и х1 как а, а расстояние между
осями у и у1 как b.
По чертежу видно, что x1 = x + b, y1 = y + a, статические моменты
сечения Sx=0 и Sy=0, т.к. оси х и у проходят через центр тяжести сечения.

18.

ТЕОРЕМА ШТЕЙНЕРА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ
18
Тогда:
S x1 y1dF y a dF ydF adF S x aF aF
F
F
F
F
F
F
F
F
S y1 x1dF x b dF xdF bdF S y bF bF
J x1 y dF y a dF y 2 dF 2 yadF a 2 dF J x 2aS x a 2 F J x a 2 F
2
2
1
F
F
F
F
F
F
F
F
J y1 x dF x b dF x 2 dF 2 xbdF b 2 dF J y 2bS y b 2 F J y b 2 F
2
2
1
F
F
J x1 y1 x1 y1dF x b y a dF xydF axdF bydF abdF
F
F
F
F
J xy aS x bS x abF J xy abF
F
F

19.

ТЕОРЕМА ШТЕЙНЕРА О ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ
19
Итак, получены формулы
при параллельном переносе осей:
S x1 аF
J x1 J x a F
S y1 bF
J y1 J y b F
2
2
J x1 y1 J xy abF

20.

ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ
20
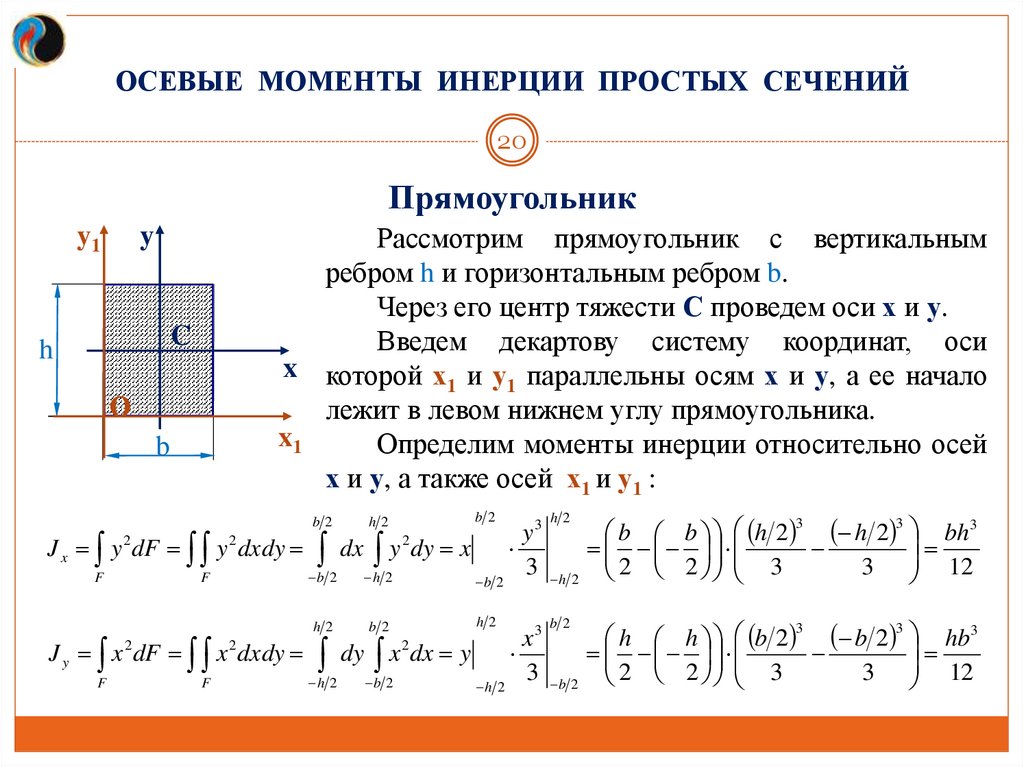
Прямоугольник
y1
y
C
h
О
b
Рассмотрим прямоугольник с вертикальным
ребром h и горизонтальным ребром b.
Через его центр тяжести С проведем оси х и у.
Введем декартову систему координат, оси
x которой х и у параллельны осям х и у, а ее начало
1
1
лежит в левом нижнем углу прямоугольника.
x1
Определим моменты инерции относительно осей
х и у, а также осей х1 и у1 :
3
3
b b h 2 h 2 bh3
y3
2
2
2
J x y dF y dxdy dx y dy x
12
3
2
2
3
3
F
F
b 2
h 2
h
2
b 2
b2
h2
b2
h2
3
3
h h b 2 b 2 hb3
x3
2
2
2
J y x dF x dxdy dy x dx y
3 b 2 2 2 3
3 12
F
F
h 2
b 2
h 2
h2
b2
h2
b2

21.

ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ
21
Осевые моменты инерции относительно осей x1 и y1:
2
bh 3 bh 3 bh 3
h
J x 1 J x bh
12
4
3
2
2
hb 3 hb 3 hb 3
b
J y J y bh
1
12
4
3
2
Итак, получено для прямоугольника:
3
bh
Jx
12
3
hb
Jy
12
bh3
J x1
3
hb 3
J y1
3

22.

ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ
22
у
Круг
R
r
О
Рассмотрим круг диаметром D = 2R. Через центр
тяжести О проведем оси х и у декартовой системы
x координат, а также введем полярную систему координат
(r, ).
2
r4
2 R 4 R 4 D 2 D 4
2
2
3
J dF r rdrd d r dr
0,1D 4
4 0
4
2
2
32
F
F
0
0
0
2
D
x
y
R
Т.к. для круга
2
R
R
4
и J J x J y то: J x J y
Итак, получено для круга:
D 4
Jx
64
D 4
Jy
64
J
2
R 4
4
D 4
Jp
32
D 4
64

23.

ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ
23
Кольцо
у
D
О d
x
Рассмотрим кольцо с внешним диаметром D и
внутренним диаметром d. Через центр тяжести
кольца – точку О, проведем оси х и у декартовой
системы координат.
D 4
d 4
D 4
d4
1 4
J
D d
32
32 32
32
D
J
Jx Jy
D4 d 4
2 64
4
4
Итак, получено для кольца:
4
J D d 4
32
4 4
J x D d
64
4 4
J y D d
64

24.

ОСЕВЫЕ МОМЕНТЫ ИНЕРЦИИ ПРОСТЫХ СЕЧЕНИЙ
24
у
Треугольник
Рассмотрим треугольник, левый нижний угол
которого поместим в начало координат. На расстоянии
h dу
у от оси х выделим элемент площади dF.
dF
Из подобия двух треугольников следует:
у
b y h y
b h y
b y
b(y)
x
О
b
h
h
площадь элементарной площадки dF :
b
b
dF b y dy h y dy
h h
h
3 h
by
by 4
bh 3
2
2 b
Тогда: J x y dF y h y dy
h
3 0 4h 0 12
F
0
bh3
Итак, получено для треугольника: J x
12

25.

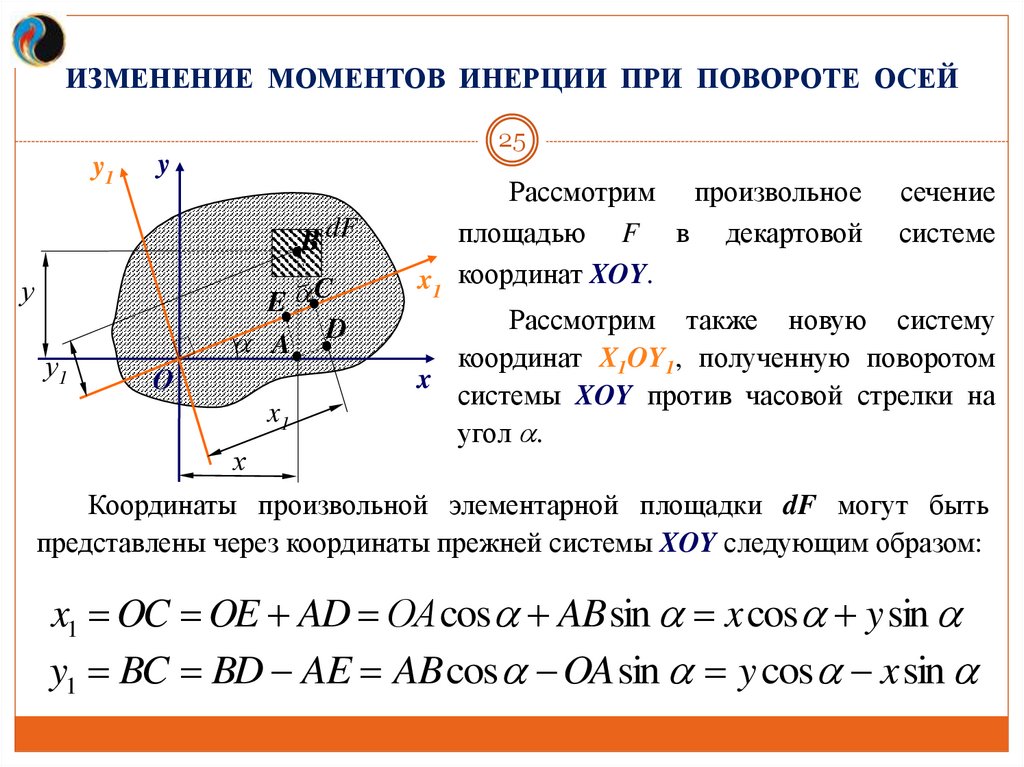
ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
25
y1
y
B dF
E C
A D
у
у1
О
x1
х
Рассмотрим произвольное
площадью F в декартовой
x1 координат XOY.
сечение
системе
Рассмотрим также новую систему
координат X1OY1, полученную поворотом
x
системы XOY против часовой стрелки на
угол .
Координаты произвольной элементарной площадки dF могут быть
представлены через координаты прежней системы XOY следующим образом:
x1 OC OE AD ОА cos AB sin x cos y sin
y1 BC BD AE AB cos OA sin y cos x sin

26.

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
26
Определим осевые и центробежный моменты инерции относительно осей х1
и у1:
J x1 y12 dF y cos x sin dF y 2 cos 2 dF 2 xy sin cos dF x 2 sin 2 dF
2
F
F
F
J x cos 2 J xy sin 2 J y sin 2 J x
F
F
1 cos 2
1 cos 2
Jy
J xy sin 2
2
2
Jy
Jy Jy
Jx
Jx Jx
1 cos 2 1 cos 2 J xy sin 2 cos 2 cos 2 J xy sin 2
2
2
2
2
2
2
Jx Jy
2
Jx Jy
2
cos 2 J xy sin 2

27.

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
27
J y1 x12 dF x cos y sin dF x 2 cos 2 dF 2 xy sin cos dF y 2 sin 2 dF
2
F
F
F
J y cos 2 J xy sin 2 J x sin 2 J y
Jy
2
F
F
1 cos 2
1 cos 2
Jx
J xy sin 2
2
2
J
J
2
2
1 cos 2 J x 1 cos 2 J xy sin 2 y y cos 2 J x J x cos 2 J xy sin 2
2
Jx Jy
2
Jx Jy
2
cos 2 J xy sin 2
2
2

28.

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
28
J x1 y1 x1 y1dF x cos y sin y cos x sin dF
F
F
xy cos 2 dF x 2 sin cos dF y 2 sin cos dF xy sin 2 dF
F
F
J xy cos 2 J y
F
F
sin 2
sin 2
sin 2
J x J y
Jx
J xy sin 2 J xy cos 2 sin 2
2
2
2
J xy cos 2
Jx Jy
2
sin 2

29.

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
29
Итак, получено:
J x1
J y1
Jx Jy
2
Jx Jy
J x1 y1
2
Jx Jy
2
Jx Jy
2
Jx Jy
2
cos 2 J xy sin 2
cos 2 J xy sin 2
sin 2 J xy cos 2

30.

ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ
30
Полученные формулы справедливы для любых центральных осей, а также
при повороте любой системы прямоугольных осей на угол .
Учитывая, что полярный момент инерции J J x J y
для системы координат X1OY1 получаем: J J x
1
J y1
т.к. оси х1 и у1 взаимноперпендикулярны.
При повороте системы координат на угол = 90 , получаем
J x1 J y
J y1 J x
J x1 y1 J xy

31.

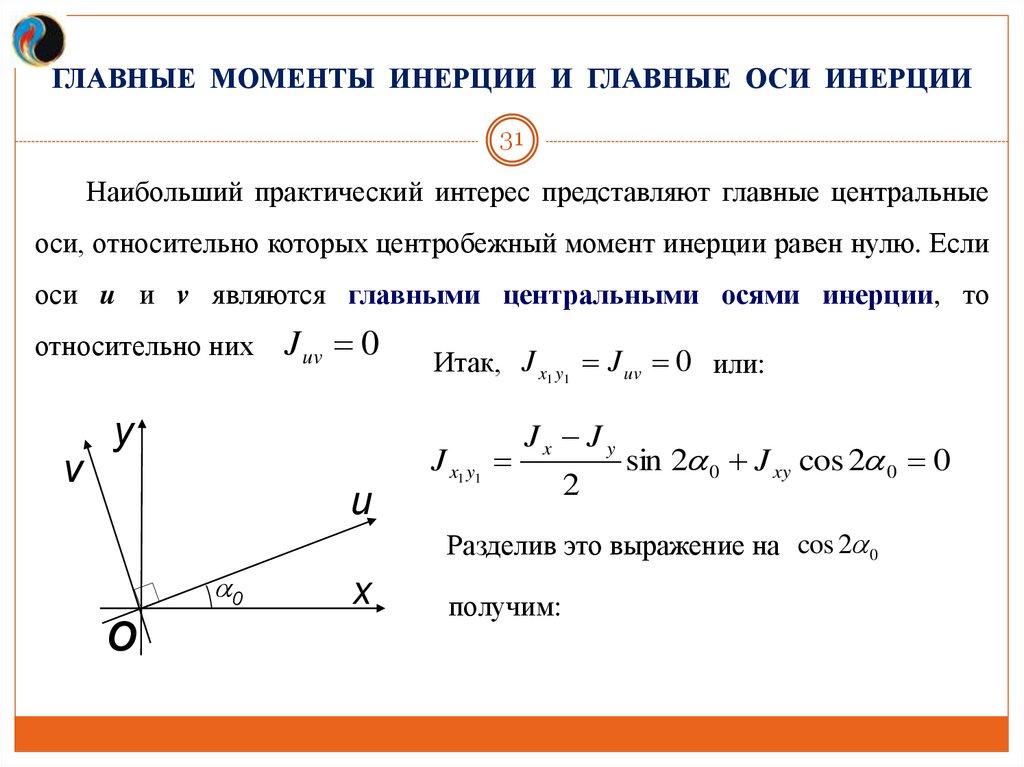
ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
31
Наибольший практический интерес представляют главные центральные
оси, относительно которых центробежный момент инерции равен нулю. Если
оси u и v являются главными центральными осями инерции, то
относительно них
J uv 0
y
Итак, J x1 y1 J uv 0 или:
J x1 y1
v
Jx Jy
u
2
sin 2 0 J xy cos 2 0 0
Разделив это выражение на cos 2 0
0
О
x
получим:

32.

ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
32
Jx Jy
2
tg 2 0 J xy
tg 2 0
2 J xy
Jy Jx
или:
2 J xy J x J y tg 2 0
Получаемые отсюда два значения угла 0 отличаются на 90 и определяют
положение главных осей.

33.

ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
33
При = 0 получаем:
J u J x cos 2 0 J y sin 2 0 J xy sin 2 0
J v J x sin 0 J y cos 0 J xy sin 2 0
2
2
Сложим и вычтем эти выражения:
J u J v J x cos2 0 J y sin 2 0 J xy sin 2 0 J x sin 2 0 J y cos2 0 J xy sin 2 0
J x cos 2 0 sin 2 0 J y sin 2 0 cos 2 0 J x J y

34.

ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
34
Ju Jv J x J y
Итак, получено:
J u J v J x cos2 0 J y sin 2 0 J xy sin 2 0 J x sin 2 0 J y cos2 0 J xy sin 2 0
J J cos 2 J J tg 2 sin 2 J J cos 2 tg 2 sin 2
J x cos 2 0 sin 2 0 J y cos2 0 sin 2 0 2J xy sin 2 0 J x J y cos 2 0 2J xy sin 2 0
x
y
0
x
y
0
0
x
y
0
0
0
cos 2 2 0 sin 2 2 0
sin 2 2 0
1
J x J y
J x J y
J x J y cos 2 0
cos 2 0
cos 2 0
cos 2 0 cos 2 0
Итак, получено:
Ju Jv
Jx Jy
cos 2 0

35.

ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
35
Теперь определим моменты инерции относительно осей u и v :
J J J J
4 J xy2
4 J xy2
1
x
y
x
y
J u J x J y J x J y 1
1
2
2
2
2
2
J x J y
J x J y
J J J J J
2
x
y
2
x
y
2
2
xy
2
2
J J J J
4
J
4
J
1
xy
x
y
x
y
xy
J v J x J y J x J y 1
1
2
2
2
2
2
J x J y
Jx Jy
J J
J J
J
2
x
y
2
x
y
2
2
xy

36.

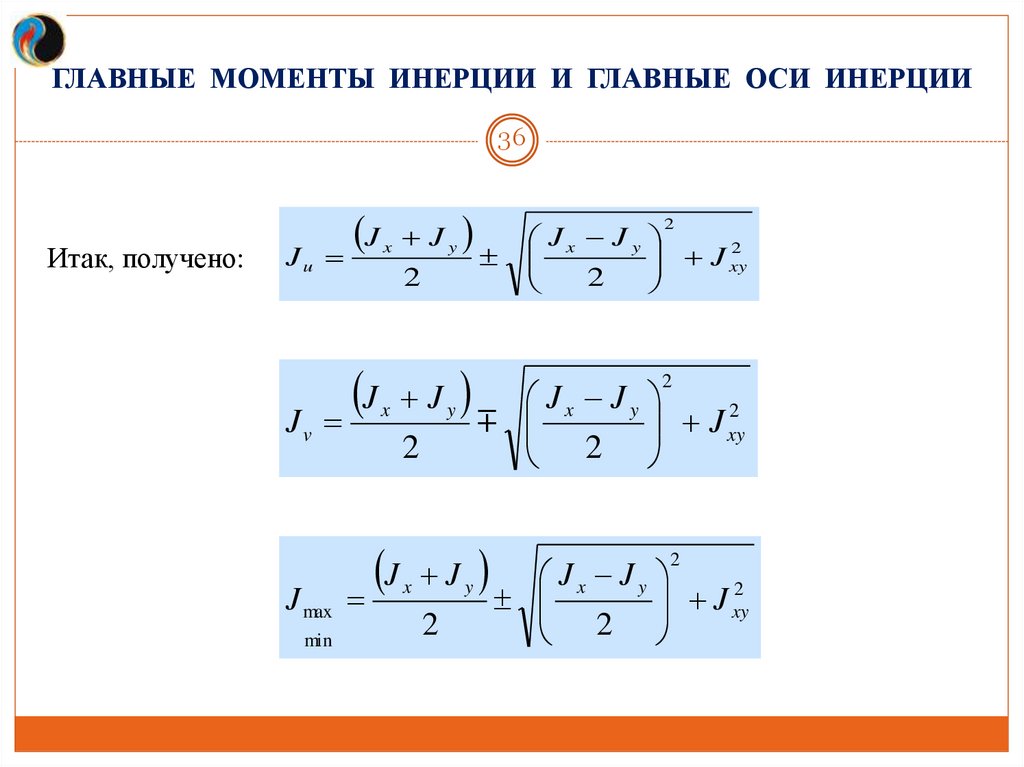
ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
36
J J J J J
J
2
xy
J J
J J
J
J
2
xy
2
Итак, получено:
x
u
y
2
x
y
2
2
x
v
y
2
x
y
2
J J
J J
J
2
J max
min
x
y
2
x
y
2
2
xy

37.

ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ И ГЛАВНЫЕ ОСИ ИНЕРЦИИ
37
Верхние знаки в полученных формулах следует брать, если Jx > Jy,
нижние – наоборот, если Jx < Jy. Т.к. оси u и v – главные, то Juv = 0,
следовательно:
Ju Jv Ju Jv
cos 2
J x1 J u cos J v sin
2
2
2
2
Ju Jv Ju Jv
cos 2
J y1 J u sin J v cos
2
2
2
2
Ju Jv
J x1 y1
sin 2
2

38.

МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ
38
Осевым моментом
сопротивления сечения изгибу называется
отношение осевого момента инерции к наибольшему расстоянию от центра
тяжести сечения до наиболее удаленной точки.
Jx
Wx
ymax
Осевой
момент
сопротивления
Jy
Wy
xmax
сечения
изгибу
может
принимать
положительные или равные нулю значения и имеет размерность [м3].

39.

МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ
39
Полярным моментом сопротивления сечения кручению называется
отношение полярного момента инерции сечения к его максимальному
полярному радиусу.
W
J
max
Полярный момент сопротивления сечения кручению может принимать
положительные или равные нулю значения и имеет размерность [м3].
Рассмотрим моменты сопротивления некоторых сечений.

40.

МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ
40
Прямоугольное сечение
y
h
О
b
Jx
bh3 2 bh 2
Wx
ymax 12 h
6
bh 2
Wx
6
Jy
b3h 2 b 2 h
Wy
xmax 12 b
6
b2h
Wy
6
x

41.

МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ
41
Круглое сечение
Jx
d 4 2 d 3
Wx Wy
ymax
64 d
32
у
Wx Wy
О
D
d 3
x
W
J
max
32
d 4 2
32 d
W
d 3
16
d 3
16

42.

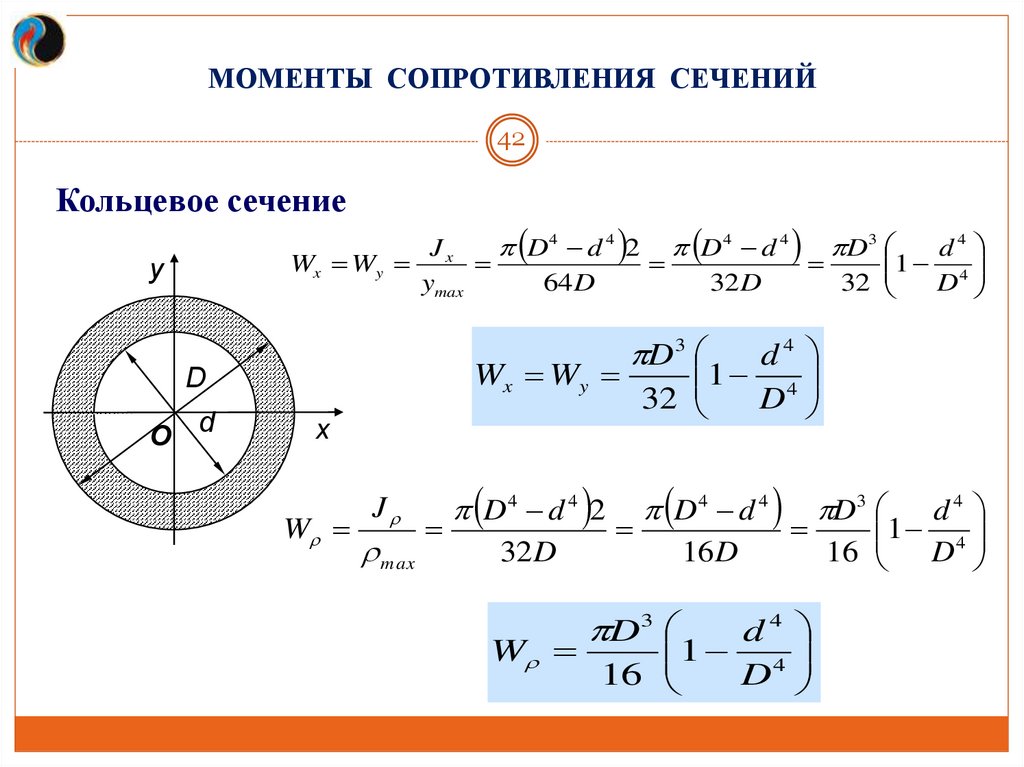
МОМЕНТЫ СОПРОТИВЛЕНИЯ СЕЧЕНИЙ
42
Кольцевое сечение
Jx
D 4 d 4 2 D 4 d 4 D3
d4
1 4
Wx Wy
ymax
64D
32 D
32
D
у
D3
d4
1 4
Wx Wy
32
D
D
О d
x
W
J
m ax
D 4 d 4 2
32 D
D 4 d 4
D3
16 D
D3
d4
1 4
16 D
d4
W
1 4
16
D