Похожие презентации:
Электрический ток в металлах. Лекция №7
1.
Лекция № 7ЭЛЕКТРИЧЕСКИЙ ТОК В
МЕТАЛЛАХ.
49
1
2.
ВОПРОСЫ20*. Переходные процессы в
конденсаторах. Разрядка и зарядка
конденсатора.
21. Классическая теория
электропроводности металлов
(теория Друде-Лоренца). Вывод
законов Ома и Джоуля-Ленца.
49
2
3.
22. Закон Видемана-Франца.Затруднения классической теории
электропроводности.
49
3
4.
494
5.
20*. Переходные процессы вконденсаторах.
Разрядка и зарядка конденсатора.
49
5
6.
Данная задача выходит за рамкиучения о постоянных токах. Решение
будем получать в условиях
квазистационарности.
Квазистационарный ток – ток,
мгновенное значение которого
одинаково во всех поперечных
сечениях провода (цепи).
Квазистационарное поле – поле,
мгновенное значение одинаково в
любой точке.
49
6
7.
Рассмотрим разрядкуконденсатора.
Если конденсатор
емкостью С зарядить до
разности потенциалов
= U = 1 2
и замкнуть на внешнее
сопротивление R, то
через него потечет ток.
49
7
8.
Обозначим черезI мгновенное значение тока;
q мгновенное значение заряда на
положительной обкладке;
U мгновенное значение
напряжения.
49
8
9.
При разрядке конденсатора заряд наобкладках убывает, поэтому силу
тока запишем так:
dq
I
dt
Также учтём, что
U = RI, q = CU.
49
9
10.
Исключаем силу тока I и напряжениеU; объединяем выражения:
dq
q
0
dt RC
Преобразуем к следующему виду:
dq dt
0
q RC
49
10
11.
Интегрируем последнее выражениеот начального момента (t = 0, q = q0)
до некоторого текущего момента
(t = t, q = q)
q
t
dq
dt
t
ln
q
ln
q
0
q q
0 RC
τ
0
здесь τ = RC = const – время
релаксации, время, за которое заряд
конденсатора убывает в «е» раз.
49
11
12.
Перепишем это выражениеследующим образом
q
t
t
ln , q q0e q0 exp
q0
τ
τ
49
t
τ
12
13.
Продифференцируем этовыражение:
q0
t
t
I exp I 0 exp
τ
τ
τ
здесь I0 = q0/τ – начальное значение
силы тока при t = 0.
49
13
14.
Зависимость заряда на обкладкахконденсатора и силы тока от
времени выглядит следующим
образом:
I0
q0
τ
t
49
14
15.
Рассмотрим зарядкуконденсатора.
Для этого в цепь
конденсатора включим
источник тока с ЭДС (Ԑ).
49
15
16.
При зарядке конденсатора заряд наобкладках возрастает, поэтому силу
тока запишем так:
dq
I
dt
Также учтём, что
q = CU.
49
16
17.
Закон Ома для неоднородногоучастка цепи запишем в виде
IR = Ԑ U,
где R сопротивление
соединительных проводов, включая
внутреннее сопротивление
источника ЭДС.
49
17
18.
Направление тока считаетсяположительным, если он течет к
положительной обкладке.
Исключив из последних трех
выражений ток и напряжение,
получим уравнение:
dq
q
dt RC R
49
18
19.
Это неоднородноедифференциальное уравнение
приведем к однородному виду:
d q С q С
0
dt
RC
49
19
20.
Интегрируем последнее выражениеот начального момента (t = 0, q0 = 0)
до некоторого текущего момента
(t = t, q = q)
d q C
dt
q C
t
0 q C 0 RC ln C τ
q
t
здесь τ = RC = const
49
20
21.
Перепишем это выражениеследующим образом
t
q qm 1 exp
τ
здесь qm = ԐC максимальное
значение заряда на конденсаторе
при t .
49
21
22.
Продифференцируем этовыражение:
qm
t
t
I exp exp I 0e
τ
τ R
τ
t
τ
здесь I0 = Ԑ/R – начальное значение
силы тока при t = 0.
49
22
23.
Зависимость заряда на обкладкахконденсатора и силы тока от
времени выглядит следующим
образом:
I0
qm
τ
t
49
23
24.
4924
25.
21. Классическая теорияэлектропроводности металлов
(теория Друде-Лоренца).
Вывод законов Ома и Джоуля-Ленца.
49
25
26.
В данной теории предполагается,что электроны проводимости в
металле ведут себя подобно
молекулам идеального газа.
В промежутках между соударениями
с ионами кристаллической решётки
они движутся совершенно свободно,
пробегая в среднем некоторый путь
λ ≈ 1 Å = 10-10 м.
49
26
27.
При этом, средняя скорость(средняя квадратичная скорость
теплового движения при T = 273 К)
ʋ ≈ 105 м/с.
Но электрический ток складывается
из упорядоченного движения
j ne u
j – плотность тока;
n – концентрация электронов;
e – заряд электрона.
49
27
28.
При следующих значенияхj ≈ 107 А/м2, n ≈ 1029 м-3,
e ≈ 1,6 * 10-19 Кл
скорость упорядоченного движения
(скорость дрейфа) равна
3
u 10
м/с.
49
28
29.
Отсюда видно, что скорость дрейфамного меньше скорости тепловой
u ʋ,
но средняя скорость дрейфа не
равна нулю, а средняя скорость
теплового движения равна нулю
ʋ = 0.
u 0
49
29
30.
Выведем закон Ома.При столкновении электрона с ионом
кристаллической решётки вся
энергия переходит иону и скорость
электрона становится равной нулю
u 0
Скорость теплового движения не
обнуляется из-за теплового
равновесия электрона и иона
кристаллической решётки.
49
30
31.
Под действием электрического поляэлектрон получит постоянное
ускорение
a = eE/m,
здесь E – напряжённость поля
электростатического поля,
m – масса электрона.
49
31
32.
за время среднего пробега(τ – время между двумя
последовательными соударениями)
его скорость будет увеличиваться до
некоторого максимального значения
eE
umax
τ
m
49
32
33.
Средняя скорость упорядоченногодвижения вдвое меньше
umax eE
u
τ
2
2m
49
33
34.
Среднее время пробега и среднеерасстояние пробега соотносятся
следующим образом:
τ
49
λ
34
35.
Таким образом, плотность токавычисляется следующим способом
eE λ ne λ
j ne u ne
E μneE
2m 2m
2
Следовательно, удельная
электропроводность
(формула Друде-Лоренца)
ne λ
σ
μne
2m
2
49
35
36.
Подвижность электроновeλ
μ
2 m
49
36
37.
Получим выражение для законаДжоуля-Ленца.
В конце свободного пробега
электрон приобретает
дополнительную кинетическую
энергию, среднее значение которой
равно
2
max
mu
Екин
2
49
eλ
2
E
2
2m
2
2
37
38.
Столкнувшись с ионом, электрон, попредположению, полностью
передаёт приобретённую энергию
кристаллической решётке.
Каждый электрон претерпевает за
секунду в среднем
1 υ
τ λ
соударений.
49
38
39.
Поэтому в единице объёма заединицу времени должна
выделяться теплота в количестве
1
ne λ 2
Qуд n Eкин
E
τ
2m
2
49
39
40.
При этом, удельноеэлектросопротивление можно
представить в виде
2m 1
ρ 2
ne λ σ
49
40
41.
Плотность токаne λ
j
E
2m
2
отсюда
Qуд ρj
2
закон Джоуля-Ленца в
дифференциальной форме
(локальной форме)
49
41
42.
4942
43.
22. Закон Видемана-Франца.Затруднения классической теории
электропроводности.
49
43
44.
Видеман и Франц установили в 1853году эмпирический закон (из опыта):
При постоянной температуре для
всех металлов отношение
коэффициента теплопроводности к
коэффициенту электропроводности
является величиной постоянной.
k / σ = const.
49
44
45.
AlCu
Pb
При 300 К
5,8·10–6 Дж·Ом/с·К;
6,4·10–6 Дж·Ом/с·К;
7,0·10–6 Дж·Ом/с·К;
При изменении температуры, данное
отношение изменяется
пропорционально
термодинамической температуре.
49
45
46.
Так как теплопроводность металловгораздо выше, чем у диэлектриков,
то предположили, что
теплопередача в металлах
осуществляется в основном не
кристаллической решёткой, а
свободными электронами.
49
46
47.
Учитывая электроны какодноатомный газ, запишем
коэффициент теплопроводности
1
k nm λcV
3
n – концентрация электронов,
m – масса электрона,
ʋ – скорость электронов,
λ – длина свободного пробега,
cV – удельная теплоёмкость
при V = const.
49
47
48.
Учтём, что удельная теплоёмкостьпри постоянном объёме
kБ 3
CV
m2
и удельная электропроводность
ne λ
σ
2 m
2
здесь kБ – постоянная Больцмана.
49
48
49.
1nk
λ
2
Б
k 2
kБ m
2
2
σ
ne λ
e
2m
2
2
2kБ m
2k Б 3
kБ
2
2 kБT 3 T
2
e
e 2
e
49
49
50.
Закон Видемана-Франца2
k
kБ
3 T
σ
e
здесь T – термодинамическая
температура.
49
50
51.
Недостаточность (затруднения)классической теории
1) При выводе формулы
2
k
kБ
3 T
σ
e
Друде не учитывал распределение
максвелла электронов по скоростям.
49
51
52.
Лоренц учёл распределение поскоростям и получил формулу
2
k
kБ
2 T
σ
e
которая плохо согласуется с
экспериментом.
49
52
53.
2) Согласно формулеne λ
σ
μne
2m
2
сопротивление должно расти как
ρ 1 σ Т
3
m
k БT
2
2
2
но экспериментальная зависимость
удельного сопротивления имеет
следующий вид ρ ρ 0 1 αt
49
53
54.
3) Электронный газ должен обладатьмолярной теплоёмкостью 3/2R, если
добавить молярную теплоёмкость
кристаллической решётки металлов
3R, то получим 9/2R, что в 1,5 раза
больше теплоёмкости диэлектриков,
в действительности они почти
равны.
49
54
55.
4) Классическая теория не можетобъяснить самого главного – почему
электроны в металлах оказываются
свободными.
49
55
56.
4956



































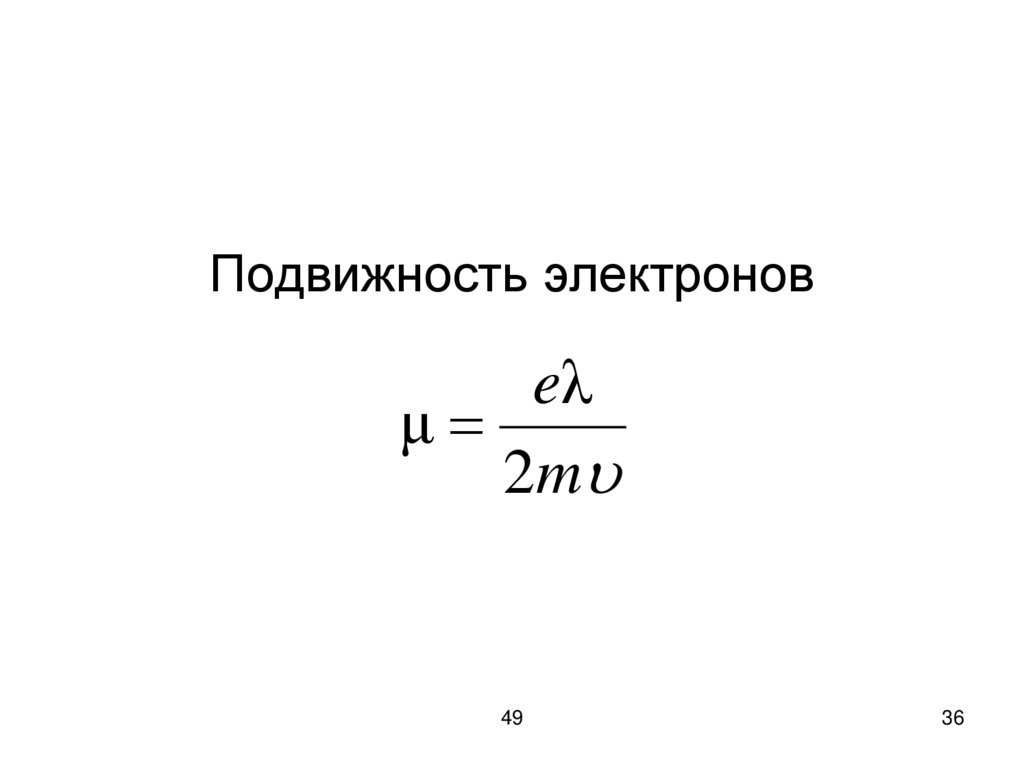




















 Физика
Физика








