Электрический ток. Лекция 24(6)

1. Электрический ток

ВоГУ
Лекция 24 (6)
Электрический ток
Кузина Л.А.,
к.ф.-м.н., доцент
2017 г.
1

2. План

2

3.

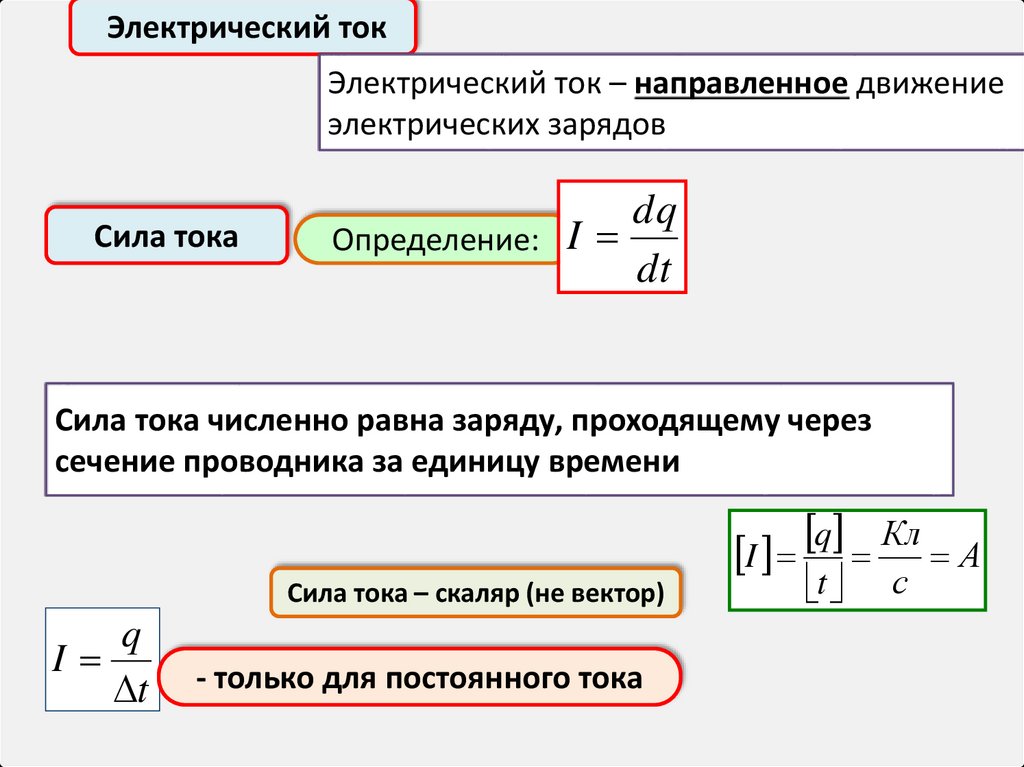
Электрический ток
Электрический ток – направленное движение
электрических зарядов
Сила тока
dq
Определение: I
dt
Сила тока численно равна заряду, проходящему через
сечение проводника за единицу времени
q Кл
I А
Сила тока – скаляр (не вектор)
q
I
t
- только для постоянного тока
t
с

4.

Плотность тока
Определение:
dI
j
dS
Плотность тока – это сила тока, приходящаяся на
единицу площади сечения проводника
I
j
S
А
м2
Плотность тока – вектор; направлен
параллельно скорости движения зарядов

5.

dI
j
dS
dI j dS – ток, проходящий через
элемент сечения проводника dS
Полный ток через поверхность S:
I dI j dS j cos dS
S
S
S

6.

v - средняя скорость направленного движения зарядов
q0 – заряд частицы
n – концентрация заряженных частиц
dN n dV
dV=Svdt
dq q0 dN – заряд, перенесённый через сечение S за dt
dq q0 n S v dt
I
q0 n S v
dt
dt
I q0 n S v
j
q0 n v
S
S
j q0 n v

7.

Электродвижущая сила (ЭДС)
Для того, чтобы ток в проводнике поддерживался, нужны сторонние
силы (неэлектростатические)
Определение:
ЭДС источника – это работа
сторонних сил по переносу
единичного заряда в цепи:
A
q
Aстор.
q
Дж
В (Вольт )
Кл

8.

Eстор.
Fстор.
q
- напряжённость поля сторонних сил
Сила, действующая на заряд: Fстор. q Eстор.
Работа сторонних сил при переносе заряда q на
произвольном участке цепи от точки 1 до точки 2:
Aстор.12
2
2
dAстор. Fстор.dl q Eстор.dl q Eстор.dl
2
2
1
1
Aстор.
q
12
1
1
2
Для замкнутого контура:
1
L
Eстор.dl
Eстор.dl

9.

E Eкул. Eстор.
F q E q Eкул. Eстор.
Напряжённость суммарного поля кулоновских
(электростатических) и сторонних сил равна:
Суммарная (полная) сила:
Работа суммарной силы при переносе заряда на участке цепи при переносе
заряда q на произвольном участке цепи от точки 1 до точки 2:
2
2
2
A12 dA F dl q Eкул. Eстор. dl q Eкул.dl q Eстор.dl
2
2
1
1
1
1
1 2 Eкул.dl
1
2
1
A12 q 1 2 q 12
Eстор.dl
2
12
1

10.

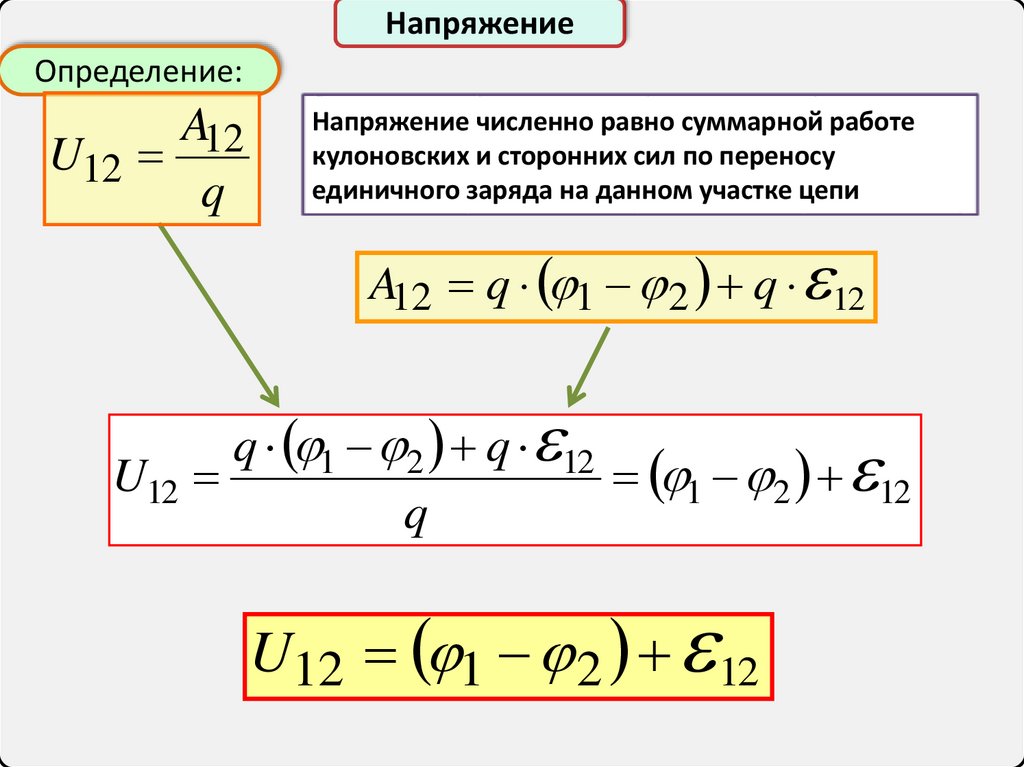
Напряжение
Определение:
A12
U12
q
Напряжение численно равно суммарной работе
кулоновских и сторонних сил по переносу
единичного заряда на данном участке цепи
A12 q 1 2 q 12
q 1 2 q 12
U12
1 2 12
q
U12 1 2 12

11.

Напряжение
U12 1 2 12
Понятие напряжения обобщает понятия разность потенциалов и ЭДС
Частные случаи:
Контур замкнут (1=2)
1 2
U
Однородный участок цепи (не
содержит ЭДС) U
12
1
2

12.

Закон Ома (для участка цепи)
Установлен экспериментально
Сопротивление проводника:
Зависит от температуры:
U
I
R
l
R
S
0 (1 t ),
R R0 (1 t )
При 00С
При температуре t0С

13.

Закон Ома в дифференциальной (локальной) форме
I
j S
I U
R
l
R
S
U E l
E
I U
U
U
E l E
j
S SR S l l l
S
Определение: 1 Удельная электропроводимость – это
величина, обратная удельному
сопротивлению
j E

14.

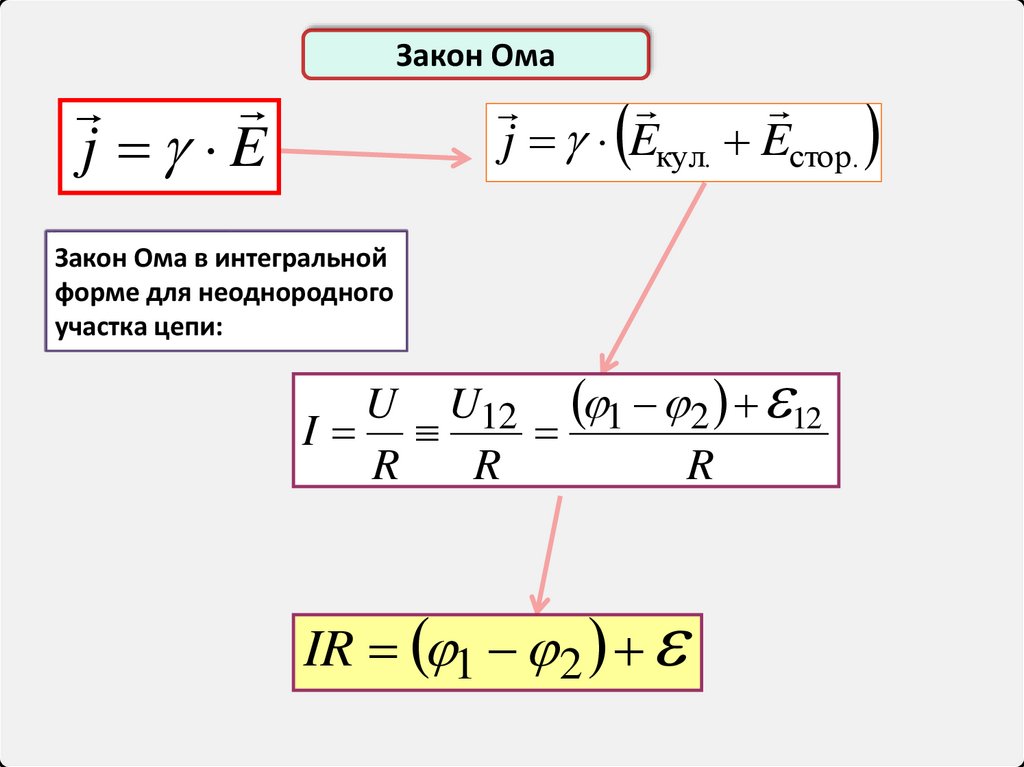
Закон Ома
j E
j Eкул. Eстор.
Закон Ома в интегральной
форме для неоднородного
участка цепи:
U U12 1 2 12
I
R
R
R
IR 1 2

15.

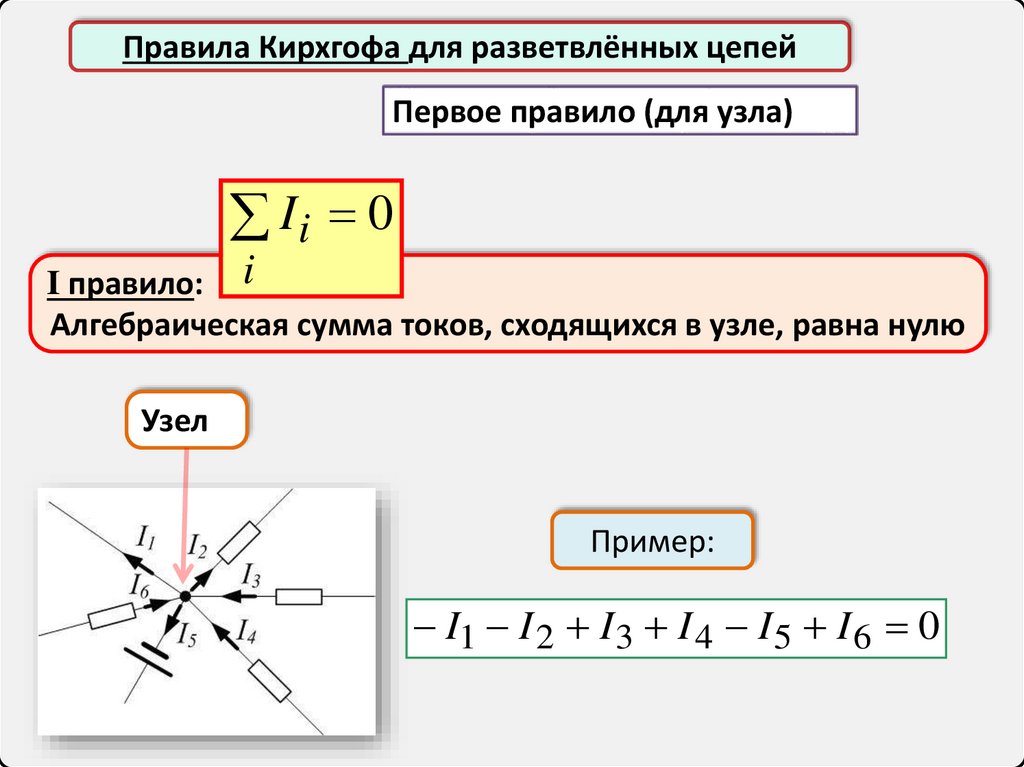
Правила Кирхгофа для разветвлённых цепей
Первое правило (для узла)
Ii 0
I правило: i
Алгебраическая сумма токов, сходящихся в узле, равна нулю
Узел
Пример:
I1 I 2 I 3 I 4 I 5 I 6 0

16.

Правила Кирхгофа для разветвлённых цепей
Второе правило (для произвольного контура)
Для каждого участка любого замкнутого контура:
IR i 1 2 i i
Просуммируем по всему замкнутому контуру с учётом, что поле
кулоновских сил потенциально:
1 2 i Eкул.dl
i
IR i i
i
0
L
i
II правило:
Алгебраическая сумма падений напряжения в любом
замкнутом контуре равна алгебраической сумме ЭДС,
включенных в данный контур

17.

Правила Кирхгофа для разветвлённых цепей
Второе правило (для произвольного контура)
Пример:
IR i i
i
i
I 5 R6 I 4 R5 I 3 R4 I 2 R2 I1R1 1 2 3

18.

Работа и мощность тока. Закон Джоуля-Ленца
Работа тока за малый промежуток времени dt по переносу заряда dq=Idt по
проводнику сопротивлением R, на который подано напряжение U равна:
dA dq U
dA dq U I U dt
Мощность тока:
P I U I I R I 2 R
U
U2
P I U U
R
R
dA I U dt
P
I U
dt
dt
2
U
P I U I R
R
2

19.

Закон Джоуля-Ленца в интегральной форме
Если работа сводится к выделению теплоты на резисторе, то:
dA dQ IUdt
Теплота, выделившаяся за конечный
промежуток времени Δt=t2 – t1:
t2
t2
t1
t1
Q dQ IUdt
t2
2
Q R I dt
t1

20.

Закон Джоуля-Ленца в дифференциальной
(локальной) форме
Удельная тепловая мощность тока равна количеству
теплоты, выделяющемуся в единице объёма
проводника за единицу времени:
dQ
w
dt V
dQ
I U dt
I U
I U
w
j E
dt V dt S l S l S l
w j E
j E
w j E E2
E j
w j E
2
j j j

21.

Процессы заряда и разряда конденсатора
А) заряд
II правило Кирхгофа
I R U
dq
I
q
dt
q
U
C
Дифф. уравнение:
Решение уравнения:
q
q R
C
t
q C 1 e RC

22.

Доказательство решения:
dq
I
q С
dt
t
q C 1 e RC
t
1 e RC
t
q C 0 e RC
C
q
e
RC
e RCt R
R
1
RC
q
q R
C
t
RC
C
t
1 e RC
C
t
t
e RC 1 e RC

23.

q C
t
1 e RC
q0 C
– максимальный заряд, до которого заряжается конденсатор
t
q (t ) q0 1 e RC
q
U
C
t
1 e RC

24.

Процессы заряда и разряда конденсатора
Б) Разряд конденсатора
II правило Кирхгофа:
I R U 0
dq
q
I
q U
C
dt
Дифф. уравнение :
Решение уравнения:
q
q R 0
C
t
q q0 e RC

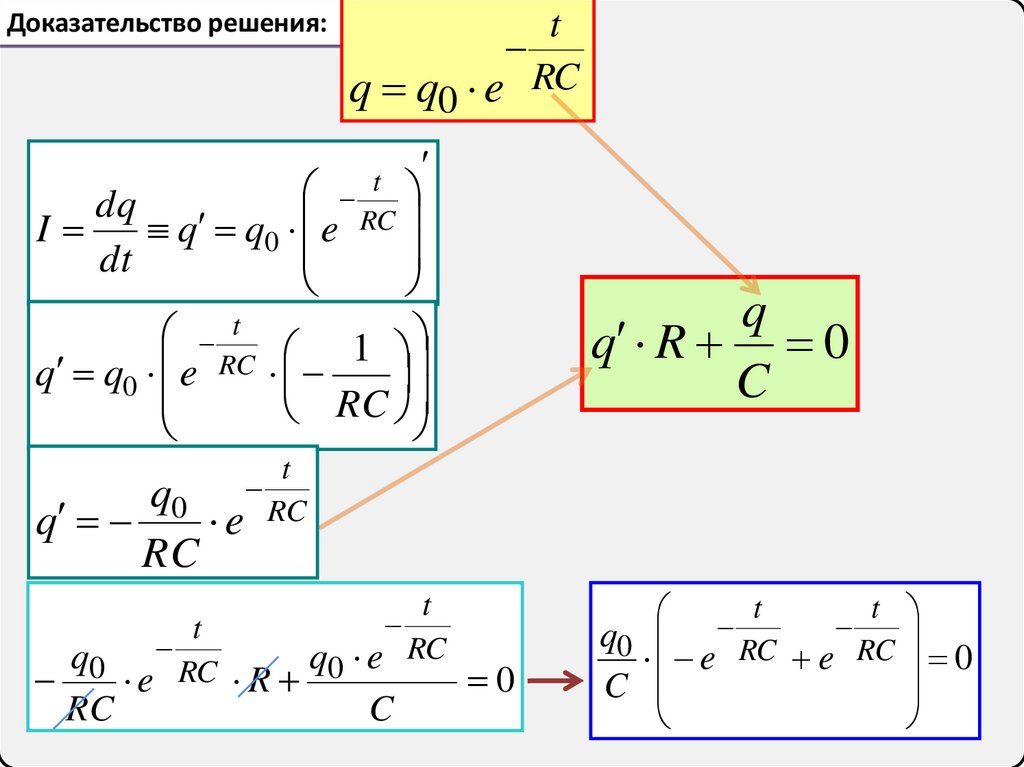
25.

Доказательство решения:
t
q q0 e RC
dq
I
q q0
dt
t 1
q q0 e RC
RC
t
e RC
q0
q
e
RC
t
RC
t
t
q0 RC
q0 e RC
e
R
0
RC
q
q R 0
C
C
t
t
q0
e RC e RC
C
0

26.

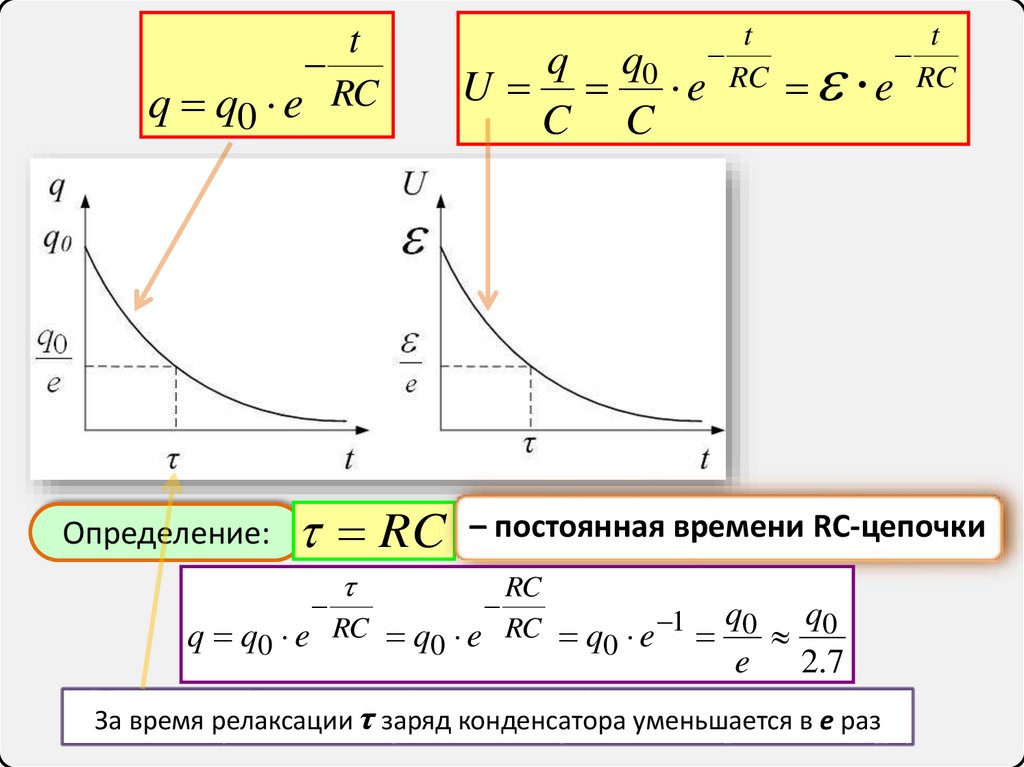
t
q q0 e RC
Определение:
RC
q q0
U e
C C
t
RC
e
t
RC
– постоянная времени RC-цепочки
RC
q0
1 q0
RC
RC
q q0 e
q0 e
q0 e
e
2.7
За время релаксации τ заряд конденсатора уменьшается в e раз