Похожие презентации:
Обнаружение когерентных сигналов со случайными параметрами. Лекция №7. Часть 1. Теоретические основы радиолокации
1.
Военно-инженерный институтДисциплина
«РАДИОЛОКАЦИОННЫЕ СИСТЕМЫ»
Часть 1. Теоретические основы радиолокации
2.
1Раскрыть
содержание
алгоритма
оптимального обнаружения сигналов с
полностью
известными
параметрами,
структуру соответствующих устройств и
методику оценки качества обнаружения этих
сигналов.
3.
21. Отношение правдоподобия и алгоритм одноканального
обнаружения сигнала с известными параметрами на фоне
квазибелого шума.
2. Оценка качества обнаружения.
4.
31. Отношение правдоподобия и алгоритм одноканального
обнаружения сигнала с известными параметрами на фоне
квазибелого шума
Pсп y t
1, при l y t l0 ,
l y t
.
ˆ y (t )
А
опт
P
y
t
п
0
,
при
l
y
t
l
.
0
Полагая, что спектры сигнала и помехи ограничены сверху частотой fмакс,
непрерывную реализацию входного сигнала y(t) в соответствии с теоремой
Котельникова можно представить совокупностью дискретных значений yk(tk),
следующих через интервалы t = 1/2 fмакс. Это позволяет свести различные
реализации функции y(t) к многомерным случайным величинам Y = {y1,y2,...,yn}
Рп Y Рп y1 , y2 ,..., yn ,
Рcп Y Рп y1 x1 , y2 x2 ,..., yn xn ,
где
xk ,
k 1, n - дискретные значения сигнала.
5.
4 l Y Р y x , y x ,..., y x .п
1
1
2
2
Р y , y ,..., y
п
1
2
n
n
Отношение правдоподобия для
сигнала с полностью
известными параметрами
n
Из некоррелированности отдельных дискрет помехи между собой
следует, что
Рп Y Рп y1 Рп y2 ... Рп yn .
1
Рп ( yk )
e
2πN 0 f макс
Pсп yk
l Y
t
e
π N0
Рсп Y
Рп Y
e
yk2
2 N 0 f макс
t
e
π N0
yk2 t
N0
.
2
yk xk t
N0
1
xk2 t
N0 k
e
п2 = N0 fмакс.
.
(1)
2
xk yk t
N0 k
lim xk2 t x 2 t dt Э,
t 0
k
(2)
.
lim x y t x t y t dt Z ,
t 0
k
k
k
(3)
6.
5l y t e
Э
N0
e
2
Z y t
N0
(4)
.
l
l0
0
z0
Рис. 1.
z
Из монотонности связи l[y(t)] и Z[y(t)] следует, что сравнение l[y(t)]
с порогом l0 эквивалентно сравнению Z[y(t)] с порогом Z0. Значение
этого порога может быть получено путем логарифмирования (4) при
условии l[y(t)] = l0:
NЭ N2 Z0
Э
2
0
0
ln l0 ln e e
Z0
N0 N0
N0
1
Z0
ln l0 Э.
2
2
1, при Z y t Z 0 ,
Aˆ опт y t
0, при Z y t Z 0 .
7.
Иллюстрация формированияР
корреляционного интеграла Z
Рсп(zн)
Рп(z)
Иллюстрация
формирования
корреляционного
интеграла
Z
от времени t
Д
от времени t 1-F
0
1-Д z0
Э
F
z
8.
Анализ (4) показывает, что для сигнала с полностью известными6параметрами
отношение правдоподобия является монотонной функцией
корреляционного интеграла Z[y(t)] (рис. 1).
l
l0
0
z0
Рис. 1.
z
Из монотонности связи l[y(t)] и Z[y(t)] следует, что сравнение l[y(t)]
с порогом l0 эквивалентно сравнению Z[y(t)] с порогом Z0. Значение
этого порога может быть получено путем логарифмирования (4) при
условии l[y(t)] = l0:
N0
1
Z0
ln l0 Э.
2
2
Таким образом,
алгоритм обнаружения заключается в определении по
наблюдаемой реализации y(t) корреляционного интеграла Z[y(t)]
и сравнении его с порогом.
9.
Структурная схема простейшего по принципу действия обнаружителя7
сигнала с полностью известными параметрами представлена на рис.2. Она
состоит из умножителя, интегратора и порогового устройства (ограничителя по
минимуму). На умножитель подается опорное колебание x(t), соответствующее
ожидаемому сигналу, и принятый сигнал y(t). Непосредственное интегрирование
произведения x(t)∙y(t) дает корреляционный интеграл. Такой обнаружитель
называется корреляционным. Величина корреляционного интеграла сравнивается
с порогом z0 порогового устройства. Опорное колебание x(t) может
вырабатываться специальным гетеродином в зависимости, например, от
установленного времени запаздывания tз, пропорционального дальности до цели.
Опорный сигнал может получаться также непосредственно от передатчика
радиолокатора через линию задержки на время tз. В общем случае зависимость
x(t) от tз обозначим как x(t, ), т.е. = tз.
y(t)
z
Умножитель
Интегратор
Пороговое
устройство
z0
x(t, )
Рис. 2.
 1, если z z0
 0, если z z0
10.
8Обнаружитель
когерентных
сигналов
с
известными
параметрами
должен
по
наблюдаемой реализации вычислять интеграл
и сравнивать его с порогом. Сигнал,
подаваемый на умножитель обнаружителя
должен соответствовать ожидаемому сигналу и
подаваться в схему с учетом времени
поступления отраженного от цели сигнала.
11.
9Определим статистические характеристики корреляционного
интеграла
z y t x t dt
Полагаем, что шум n(t) распределен по нормальному закону с
нулевым математическим ожиданием
M n t n t 0.
При y(t) = n(t) получим
M z M n t x t dt 0.
При наличии сигнала y(t) = x(t) + n(t)
M z M n(t ) x(t ) x 2 (t ) dt x t M n t dt x 2 t dt Э,
где Э - энергия сигнала.
12.
и при наличии сигнала и10 Дисперсия Z одинакова в отсутствие
равна
2
2
М z M z M z M n t x t dt n τ x τ dτ
M n t n τ x t x τ dtdτ.
Корреляционная функция «белого» шума
N0
M n t n τ
δ t τ ,
2
Одно из важных свойств дельта –
функции – так называемое фильтрующее
свойство - состоит в том, что если дельта –
функция присутствует под интегралом в
качестве
множителя,
то
результат
интегрирования будет равен значению
остального подынтегрального выражения в
той точке, где сосредоточен дельта – импульс:
Если значение t0 не попадает в интервал
интегрирования, интеграл равен нулю.
f (t ) (t t )dt f (t )
0
0
где N0 - спектральная плотность шума.
Учитывая фильтрующее свойство дельта-функции, находим
N 0Э
М z
02 .
2
2
Поскольку величина Z является линейной комбинацией входных
величин n(t) и x(t), то она также распределена по нормальному
z2
2
закону.
1
2 0
P
z
e
.
Тогда, если принимается только шум, то
п
2π
13.
11 Если на входе есть и сигнал, и шум, то получаем распределениесо средним
z Э
Рсп z
1
2π 0
e
z Э
2
2 02
.
Кривая Рсп(z) = Рп(z-Э) представляет собой сдвинутую на величину
Э кривую Рп(z).
Показатели качества обнаружения РЛ сигнала определяются
следующими выражениями:
Д Pсп z dz;
z0
Р
F Pп z dz.
z0
Рсп(zн)
Рп(z)
Д
1-F
0
1-Д z0
Э
F
z
(5)
14.
12z
Рп zн
0
z
Рcп zн
0
1
e
2π
zн2
2
1
e
2π
;
(6)
zн q
2
2
,
Вводя нормированное значение корреляционного интеграла zн = z/υ0
и учитывая, что Д[zн] = 1, получим
где q
Д
q0
Э
0
1
e
2π
2Э
N 0 - параметр обнаружения сигнала (отношение сигнал/шум на
выходе схемы оптимальной обработки).
Подставляя соотношения (6) в (5), приходим к равенствам
2
zн q
2
1 1
dzн Ф q q0 ;
2 2
F
(7)
где q0 = z0/υ0 - нормированный уровень порога;
q0
1
e
2π
2
zн
2
dzн
1 1
Ф q0 ,
2 2
(8)
15.
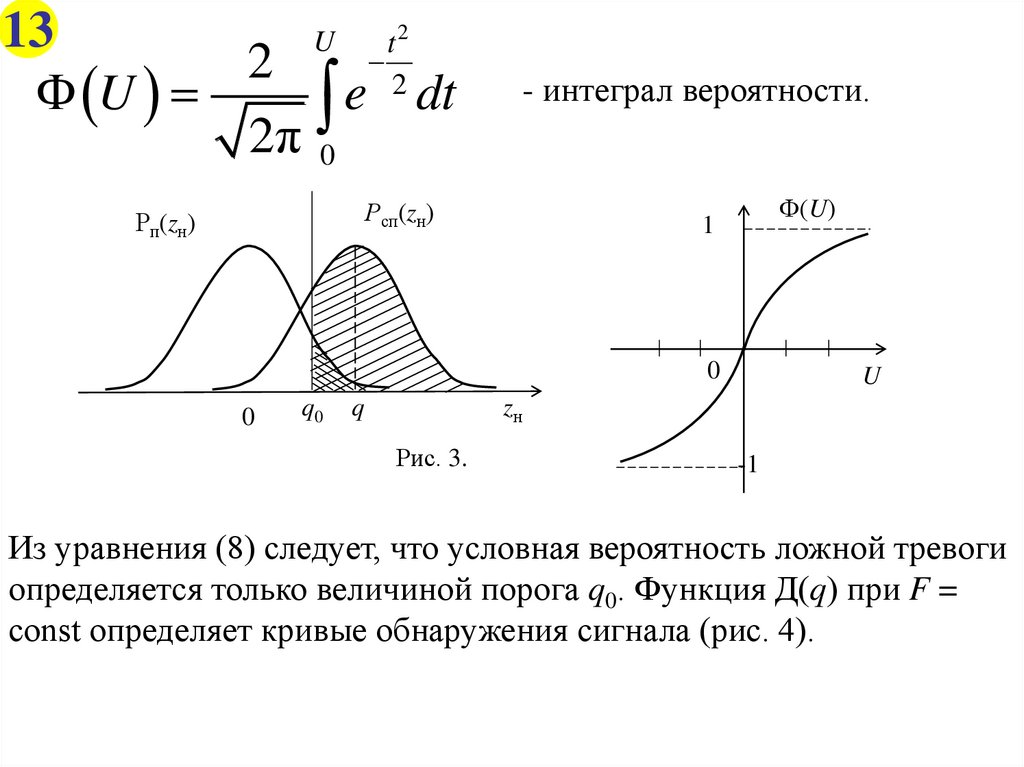
13U
t2
2
2
Ф U
e
dt
2π 0
- интеграл вероятности.
Рсп(zн)
Рп(zн)
Ф(U)
1
0
0
q0
q
U
zн
Рис. 3.
-1
Из уравнения (8) следует, что условная вероятность ложной тревоги
определяется только величиной порога q0. Функция Д(q) при F =
const определяет кривые обнаружения сигнала (рис. 4).
16.
14Д
D
F1
F2
0,5
F1
F2
0
q01
q02
F1>F2
Рис. 4.
q
Задавая F по соотношению (8), определяем q0, а затем, зная q0, с
помощью (7) строим графики Д(q). Из приведенных на рис. 4
кривых следует, что для обеспечения одной и той же Д при
меньшем F нужна большая энергия сигнала.
17.
15Заключительная часть
1. Оптимальный обнаружитель должен вычислять корреляционный
интеграл и сравнивать с порогом.
2. Качество обнаружения сигналов не зависит от их формы и
определяется энергетическим отношением сигнал/шум.
Задание на самостоятельную подготовку:
Отработать материал лекции
рекомендованной литературой.
Л 1/о с. 134-140;
Л 1/д с. 97-104;
Д 2/д с. 126-130.
в
соответствии
с
















 Физика
Физика Военное дело
Военное дело








