Похожие презентации:
Приращение функции
1. Тема урока:Приращение функции
2. Цели урока:
Формирование понятия приращенияфункции и приращения аргумента,
секущей, геометрического смысла
приращения функции;
Развитие вычислительных навыков;
Воспитание познавательного
интереса к предмету.
3. Нахождение значения функции в точке.
Найти значение функции f(x)= x2 + 2xв точке x0 = -3.
Решение: f(x0) = f(-3) = (-3)2+ 2∙(-3)
=9-6=3
Ответ: f(-3) = 3
4. Дан график функции у=4-х2 По графику найти значение функции в точке х1=1 и х2=2
Дан график функции у=4-х2По графику найти значение функции
х1=1 и х2=2
в точке
f(1)=3, f(2)=0
3
1
2
5.
Дан график функции у=4-х2По графику найти значение
функции в точке х1=1 и
х2=2
у
4
3
Разность х2 - х1=2-1=1; ∆x=1
2
∆f
f (1)=3; f(2)=0; f(2)- f(1)=0-3= -3
∆f=-3
1
-2
-1
0
1
2
∆x
х
6.
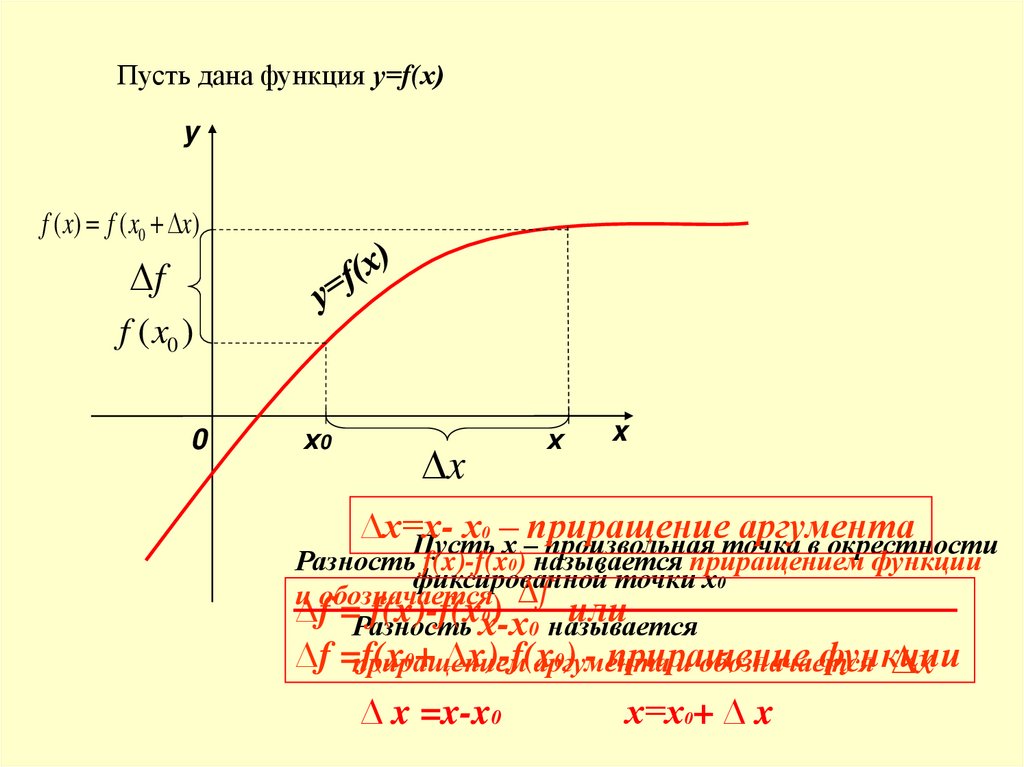
Пусть дана функция у=f(х)y
f ( x) f ( x0 x)
f
f ( x0 )
0
х0
x
х
x
∆х=хх0 – приращение аргумента
Пусть х – произвольная точка в окрестности
Разность f(x)-f(x0) называется приращением функции
фиксированной точки х0
и обозначается f
∆f =Разность
f(x)-f(xх-х
0)
или
0 называется
∆f =f(x
0+ ∆x)-f(x
0) - приращение
функции
приращением
аргумента
и обозначается
x
∆ x =x-x0
х=х0+ ∆ x
7.
• Определение.Приращением аргумента функции
называется величина, равная разности
между конечным и начальным
значением аргумента: ∆ x =x-x0
• Определение.
Приращением функции называется
величина, равная разности между
конечным и начальным значением
функции ∆f =f(x) - f(x0) = f(х0 + х)– f(x0).
8.
• Δ, δ (название: де́льта, греч. δέλτα) — 4-ябуква греческого алфавита. В системе
греческой алфавитной записи чисел имеет числовое
значение 4. Происходит от Финикийской буквы —
далет, название которой означало «дверь» или «вход в
палатку». От буквы «дельта» произошли латинская
буква D и кириллическая Д. Обозначение приращения
функции (аргумента) буквой дельта впервые применил
швейцарский математик и механик Иоганн Бернулли
(1667-1748)
9. Пример 1
• Найти приращение аргумента иприращение функции y=x2 при переходе
от х0=1,2 к точке х=2,5
Решение: ∆ x= х-х0
∆ x=2,5-1,2=1,3,
∆f =f(x) - f(x0)
∆f=2,52-1,22=6,25-1,44= 4,81
Ответ: 1,3; 4,81
10.
Пример 2:Найти приращение аргумента и приращение
2
функции в точке х0, если
f ( x) x
x 1, 9
Решение:
x0 2
x x x0 ;
x 1, 9 2 0,1;
f f ( x) f ( x0 );
f f (1,9) f (2) 1,9 2 3,61 4 0,39
2
2
Ответ : x 0,1; f 0, 39
11. Геометрический смысл приращения функции
Геометрический смысл приращенияy
функции
y=kх+b
В
f ( x) f ( x0 x)
f
f ( x0 )
0
А
х0
f
С
x
x
х
k tg
ABC - прямоугольный
x
BC
tg
AC
Прямая l , проходящая через
любые две точки графика функции,
-угловой коэффициент
называется секущей к графику
секущей к графику
функции.
функции
f
k tg
x
12. Найти угловой коэффициент секущей к графику функции f(x) = , проходящей через точки с данными абсциссами х1 и х2. Какой угол
(острый или тупой) образует секущая с осью Ох.f(x) = x2; x1 = 0; x2 = 1
Решение tgα =
Δx = x – x0;
Δf = f(x) - f(x0);
Δx = 1 – 0 = 1; Δf = f(1) - f(0) = · 12 - · 02 =
k = tgα = > 0, значит α – острый
Ответ: tgα =
; α - острый
13. Найдите приращение функции f в точке х0, если f(x) = 3x+1, x0 = 5, ∆x = 0, 01.
Решение: х=х0+∆x, х= 5+0,01=5,01f(х0)=f(5)=3·5+1=16;
f (x)=f(5,01)= 3·5,01+1=16,03
Δf = f(x) - f(x0); Δf = 16,03-16=0,03
Ответ: 0,03
14. Найти приращение функции y=f(x) при переходе от точки х к точке х+∆x, если f(x)= х2 .
Решение: Δf = f(x) - f(x0)=f(х+ ∆x)-(x)f(x)=x2
f(х+ ∆x) =(х+ ∆x)2=x2+2x∆x+∆x2
Δf= x2+2x∆x+∆x2 - x2=2x∆x+∆x2
Ответ: 2x∆x+∆x2
15. Ответить на вопросы
• 1. Что такое приращение функции?• 2. Что такое приращение аргумента?
• 3. Объяснить в чём заключается
геометрический смысл отношения
приращения функции и приращения
аргумента
















 Математика
Математика