Похожие презентации:
Объём и площадь поверхности прямой призмы
1.
2. Задачи
Познакомитьсяс понятием объем многогранника
2. его свойствами
3. Формулами для нахождения площади
поверхности и объема многогранника
Научимся применять формулы при решении
задач
Рекомендации
При работе с презентацией
1.
3.
1 Запишите в тетрадь основныетеоретические положения и формулы
2 В разделе «решение задач» постарайтесь
решить задачи самостоятельно а затем,
проверьте его по материалу презентации.
Условие и решение запишите в тетрадь
4.
Ответьте на вопросы1)
2)
3)
4)
5)
Какой многогранник называется призмой?
Какая призма называется прямым?
Какая призма называется правильной?
Что является основанием правильной
треугольной призмы?
Чем являются боковые грани призмы?
Прямой призмы? Правильной призмы?
5. Величина части пространства, занимаемого геометрическим телом, называется объемом этого тела
6. Единицы объема
За единицуизмерения объемов
примем куб, ребро
которого равно
единице измерения
отрезков.
Куб с ребром 1 см
называют кубическим
сантиметром и
обозначают см3.
7. Свойства объемов
10. Равные телаимеют равные
объемы
8. Объем прямоугольного параллелепипеда. Теорема. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
9. Следствие 1 Объем прямоугольного параллелепипеда равен произведению площади основания на высоту Следствие 2. Объем прямой
10.
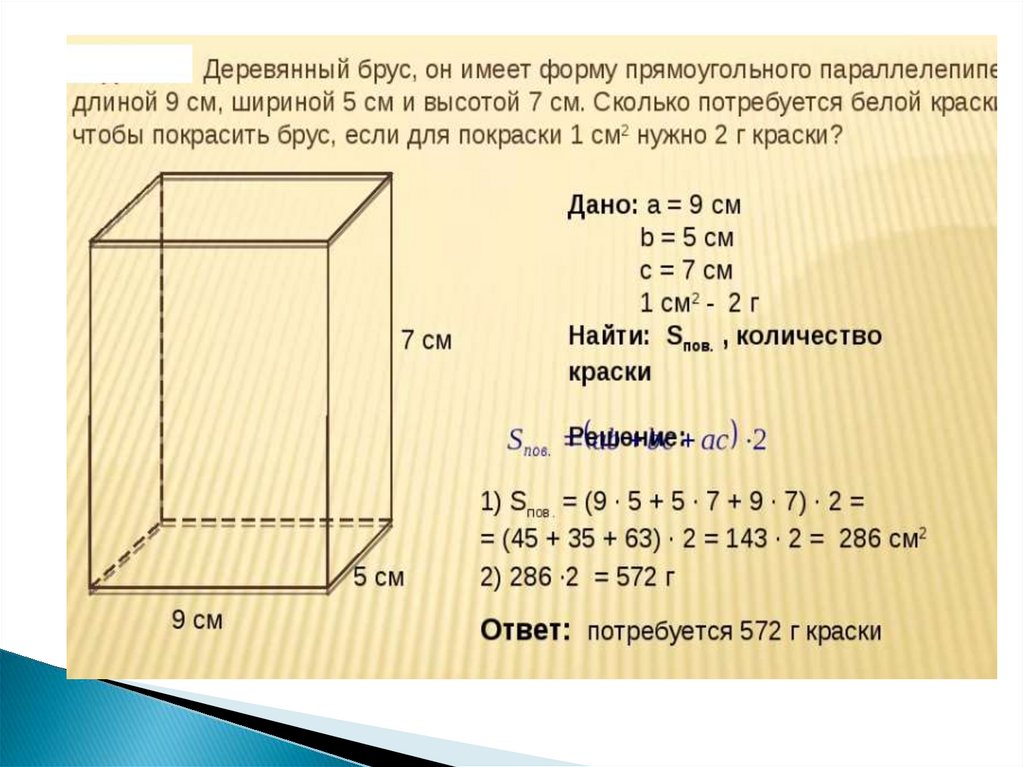
Решение задач11.
12.
13.
14. Выберите неверное утверждение
а) За единицу измерения объемовпринимается куб, ребро которого равно
единице измерения отрезков;
б) тела, имеющие равные объемы, равны;
в) объем прямоугольного параллелепипеда
равен произведению трех его измерений;
г) объем куба равен кубу его ребра;
д) объем прямоугольного параллелепипеда
равен произведению площади основания на
высоту.
е) Сформулируйте свойства объемов?
.
15.
16.
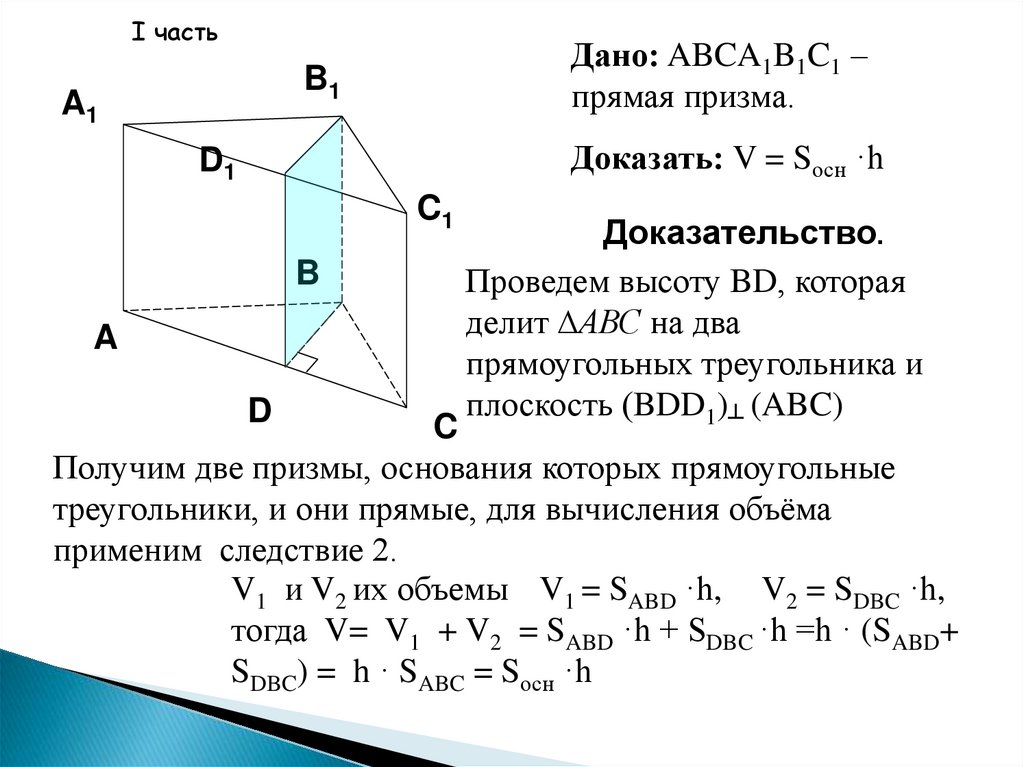
I частьДано: ABCA1B1C1 –
прямая призма.
B1
A1
Доказать: V = Sосн ·h
D1
C1
B
A
D
Доказательство.
Проведем высоту BD, которая
делит ∆АВС на два
прямоугольных треугольника и
плоскость (BDD1)┴ (ABC)
C
Получим две призмы, основания которых прямоугольные
треугольники, и они прямые, для вычисления объёма
применим следствие 2.
V1 и V2 их объемы V1 = SABD ·h, V2 = SDBC ·h,
тогда V= V1 + V2 = SABD ·h + SDBC ·h =h · (SABD+
SDBC) = h · SABC = Sосн ·h
17.
Решение задач18.
19.
II частьРассмотрим n-угольную
произвольную призму. Ее
можно разбить на (n -2)
прямые призмы (рис. 1). Объём
каждой треугольной призмы
можно вычислить применяя
I часть теоремы
S3
S1
(рис. 1)
S2
V= V1+V2+ V3+…+ Vn-2
=S1 ·h +S2 ·h+S3 ·h+…+
Sn-2 ·h = h · (S1 + S2 +S3
+…+Sn-2 ) = Sосн ·h
Т. о. V= Sосн ·h
20.
21.
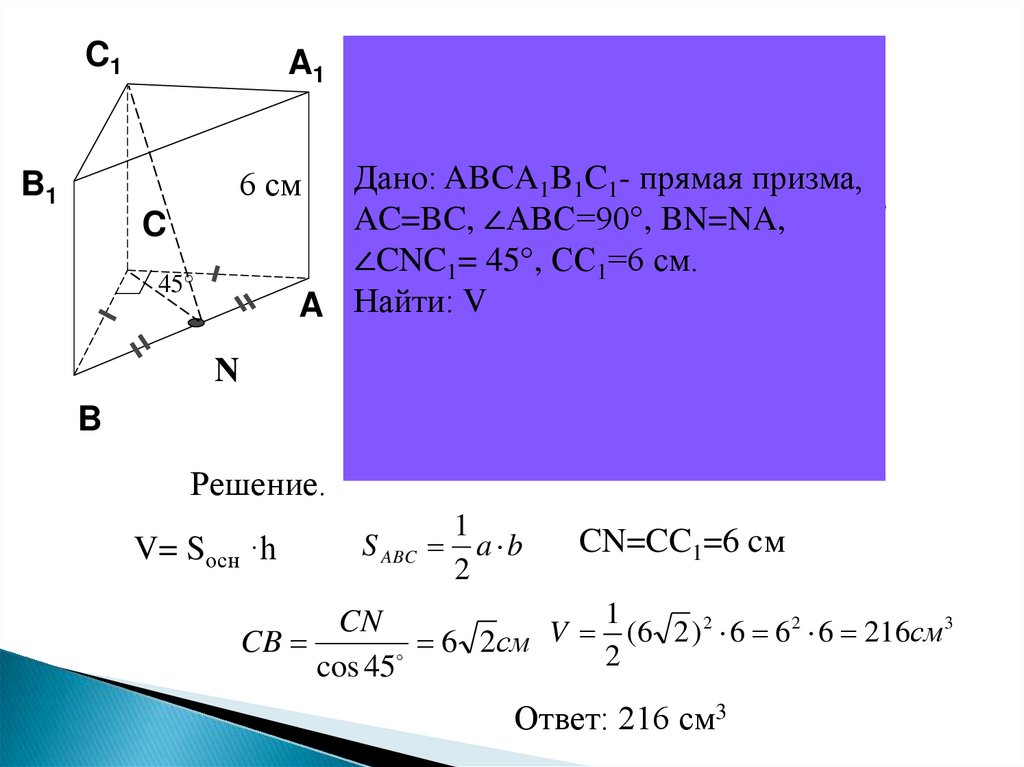
C1B1
B
A1 В основании прямой призмы лежит
прямоугольный равнобедренный
треугольник
АВС.
Дано:
ABCA
6 см
1B1C1- прямая призма,
∠АСВ =90°,
АС=СВ,BN=NA,
точка N делит
AC=BC,
∠АВС=90°,
C
гипотенузу
пополам.
∠CNC
=
45°,
СС1=6 см.
1
45°
V С1N составляет угол 45° с
Отрезок
A Найти:
плоскостью основания.
N
Боковое ребро равно 6 см.
Решение.
V= Sосн ·h
Найти объём призмы.
S ABC
1
a b
2
CN=CC1=6 cм
1
2
2
3
CN
V
(
6
2
)
6
6
6
216
см
CB
6 2см
2
cos 45
Ответ: 216 см3
22.
B1C1
Основанием прямой призмы
является ромб, острый угол
A1
D1
ABCDA
1B1C1D1- прямая призма,
2 Дано:
которого
60°.
ABCD – ромб, ∠ВАD=60°, BB1=2,
Боковое ребро равно 2.
B
C ∠B1DВ= 45°.
45°
Найти: V диагональ призмы составляет
Меньшая
60°
с плоскостью основания угол 45°.
A
D
Найти объём призмы.
Решение.
V= Sосн ·h
S ABCD a b sin
∆ABD - равносторонний
AB=BD=2, т. к. ∆B1BD - равнобедренный
V 22 sin 60 2 4 3
Ответ:
4 3
23.
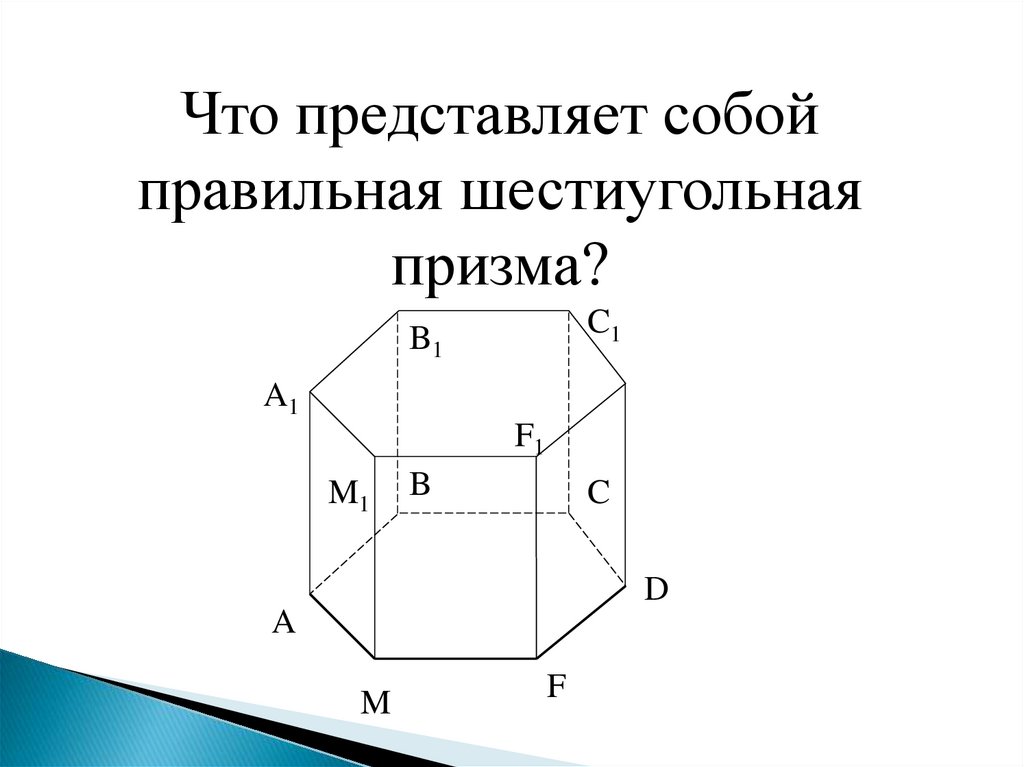
Что представляет собойправильная шестиугольная
призма?
C1
B1
A1
F1
M1
B
C
D
A
M
F
24.
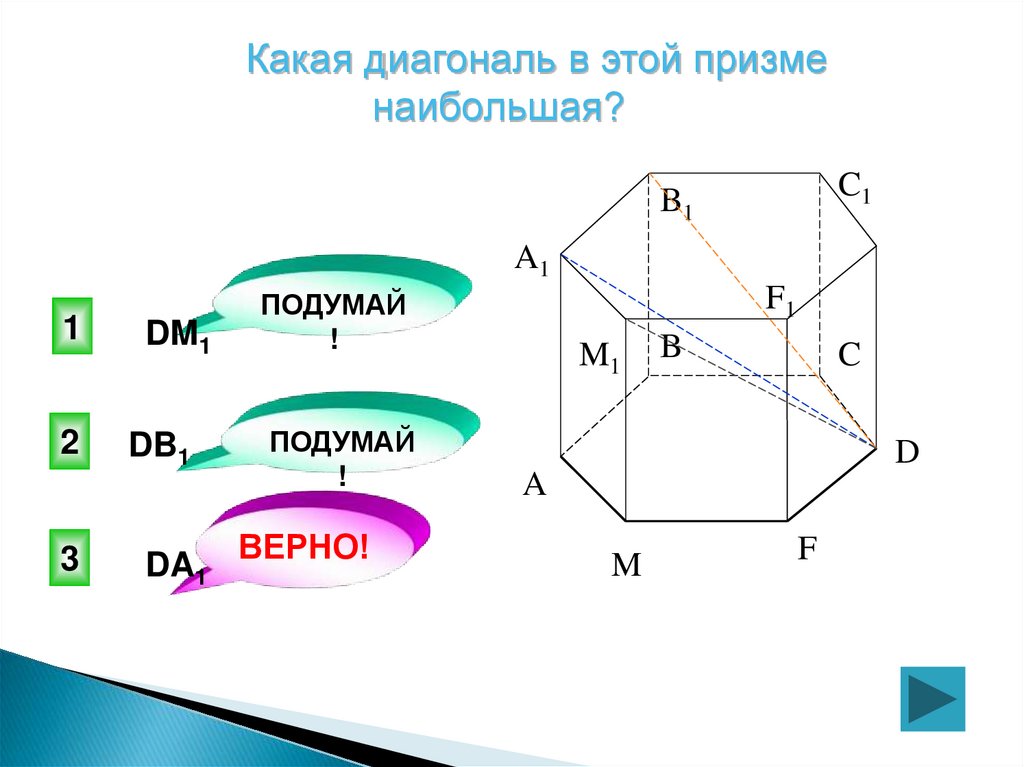
Какая диагональ в этой призменаибольшая?
C1
B1
A1
1
DM1
2
DB1
3
DA1
F1
ПОДУМАЙ
!
ПОДУМАЙ
!
ВЕРНО!
M1
B
C
D
A
M
F
25.
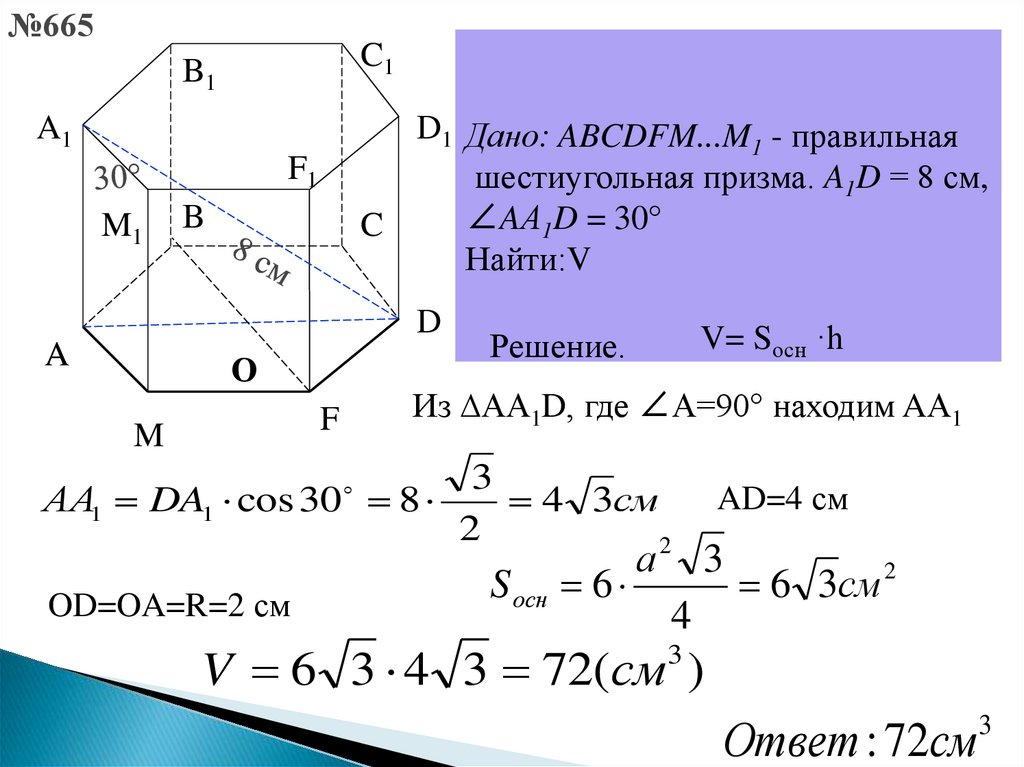
№665C1
B1
Наибольшая диагональ
D1 Дано:
правильной
шестиугольной
ABCDFM...M
1 - правильная
призмы равна 8призма.
см
шестиугольная
A1D = 8 см,
∠AА
C
1D = 30° с боковым
и составляет
Найти:V
ребром угол в 30°.
A1
F1
M1
B
D
A
О
Из ∆AА1D, где ∠А=90° находим AА1
F
M
Найти
объём призмы.
V= Sосн ·h
Решение.
3
АA1 DA1 cos 30 8
4 3см
2
2
OD=OA=R=2 см
S осн 6
а
4
AD=4 см
3
6 3см 2
V 6 3 4 3 72(см )
3
Ответ : 72см
3
26.
ИтогиОтветьте на вопросы:
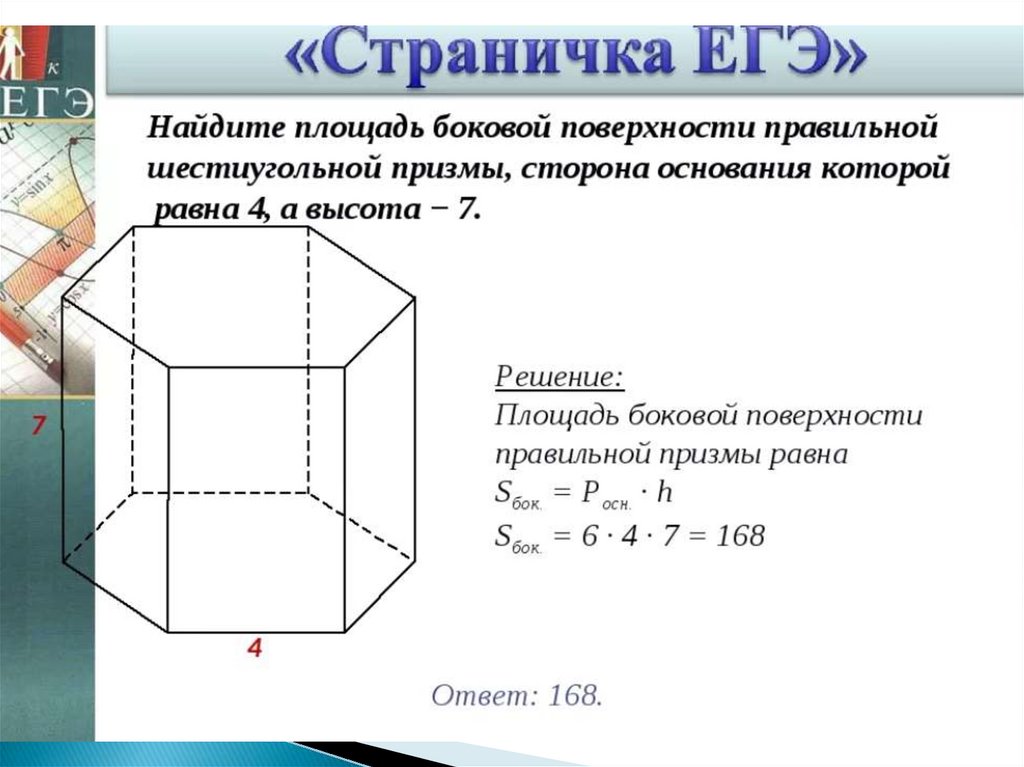
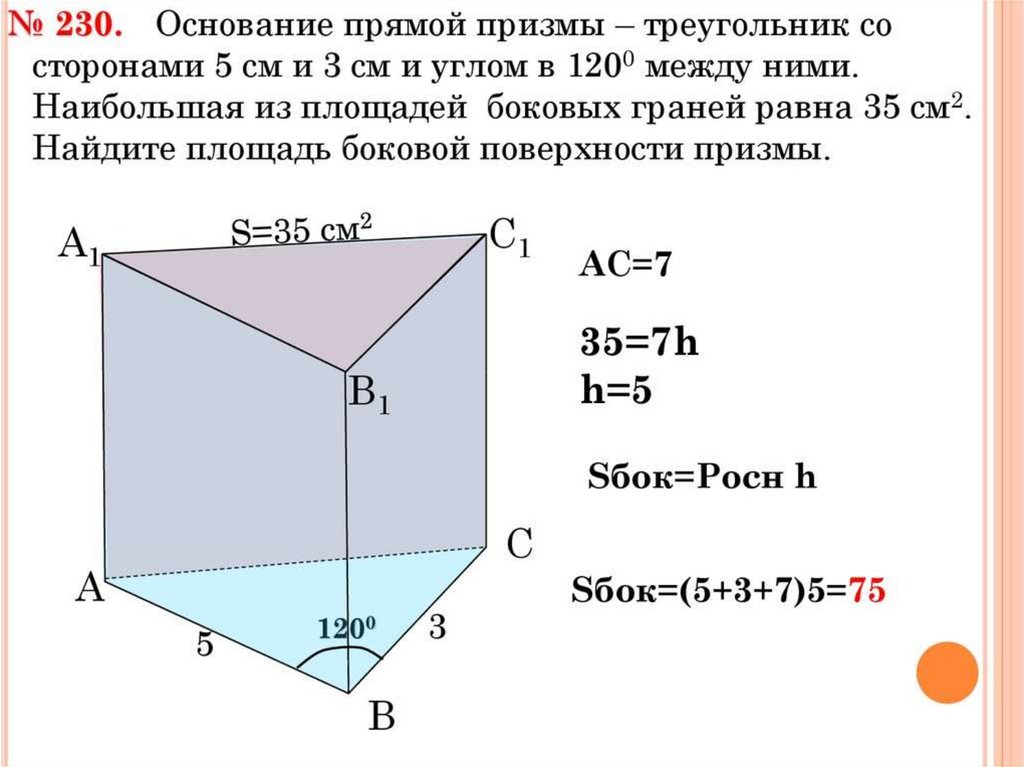
1. Как вычисляется площадь боковой и полной поверхности
призмы?
2.Как вычисляется объем прямой призмы, основанием
которой является прямоугольный треугольник?
3. Как вычисляется объем правильной треугольной призмы?
4. Как вычисляется объем правильной четырехугольной
призмы?

















 Математика
Математика








