Объем призмы. Урок геометрии в 11 классе

1.

Урок геометрии в 11 классе
Учитель математики Манджиева Н.И.

2.

а)
б)
в)
г)
д)
Какой многогранник называется призмой?
Какая призма называется прямым?
Какая призма называется правильной?
Что является основанием правильной
треугольной призмы?
Чем являются боковые грани призмы?
Прямой призмы? Правильной призмы?

3. Выберите неверное утверждение

а) За единицу измерения объемов
принимается куб, ребро которого равно
единице измерения отрезков;
б) тела, имеющие равные объемы, равны;
в) объем прямоугольного параллелепипеда
равен произведению трех его измерений;
г) объем куба равен кубу его ребра;
д) объем прямоугольного параллелепипеда
равен произведению площади основания на
высоту.
е) Сформулируйте свойства объемов?
.

4.

5.

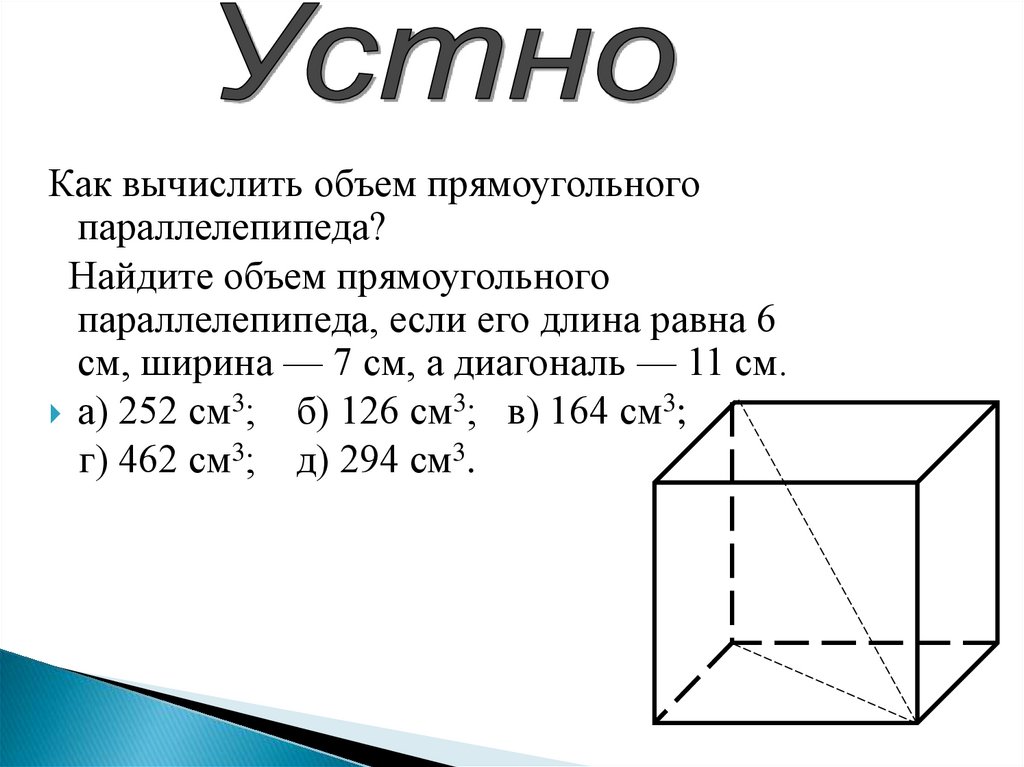
Как вычислить объем прямоугольного
параллелепипеда?
Найдите объем прямоугольного
параллелепипеда, если его длина равна 6
см, ширина — 7 см, а диагональ — 11 см.
а) 252 см3; б) 126 см3; в) 164 см3;
г) 462 см3; д) 294 см3.

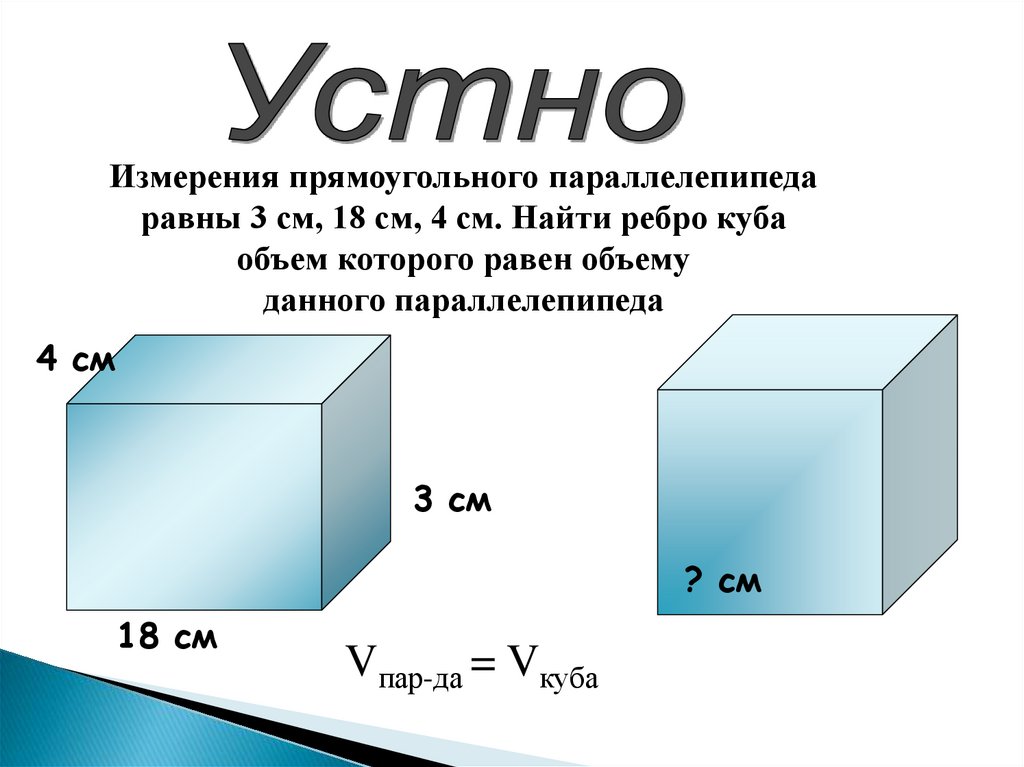
6.

Измерения прямоугольного параллелепипеда
равны 3 см, 18 см, 4 см. Найти ребро куба
объем которого равен объему
данного параллелепипеда
4 см
3 см
? см
18 см
Vпар-да = Vкуба

7.

Сформулируйте следствие из
теоремы об объеме
прямоугольного параллелепипеда,
в основании которого
прямоугольный треугольник.

8.

Теорема. Объём прямой
призмы равен
произведению площади
основания на высоту.

9.

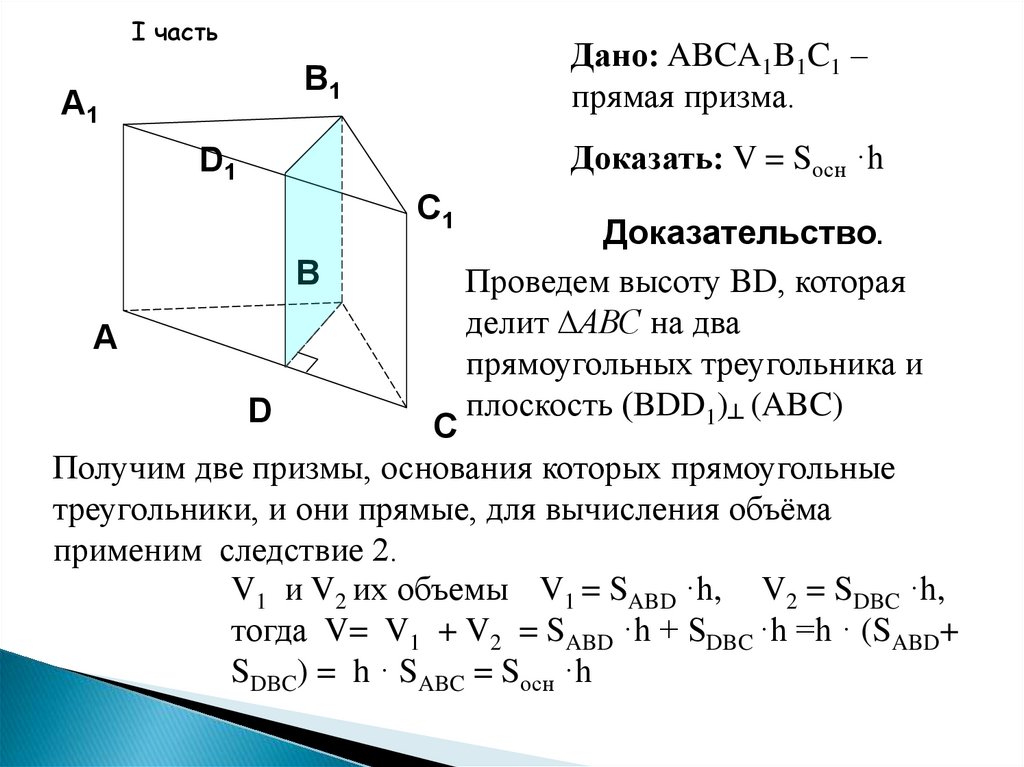
I часть
Дано: ABCA1B1C1 –
прямая призма.
B1
A1
Доказать: V = Sосн ·h
D1
C1
B
A
D
Доказательство.
Проведем высоту BD, которая
делит ∆АВС на два
прямоугольных треугольника и
плоскость (BDD1)┴ (ABC)
C
Получим две призмы, основания которых прямоугольные
треугольники, и они прямые, для вычисления объёма
применим следствие 2.
V1 и V2 их объемы V1 = SABD ·h, V2 = SDBC ·h,
тогда V= V1 + V2 = SABD ·h + SDBC ·h =h · (SABD+
SDBC) = h · SABC = Sосн ·h

10.

II часть
Рассмотрим n-угольную
произвольную призму. Ее
можно разбить на (n -2)
прямые призмы (рис. 1). Объём
каждой треугольной призмы
можно вычислить применяя
I часть теоремы
S3
S1
(рис. 1)
S2
V= V1+V2+ V3+…+ Vn-2
=S1 ·h +S2 ·h+S3 ·h+…+
Sn-2 ·h = h · (S1 + S2 +S3
+…+Sn-2 ) = Sосн ·h
Т. о. V= Sосн ·h

11.

C1
B1
B
A1 В основании прямой призмы лежит
прямоугольный равнобедренный
треугольник
АВС.
Дано:
ABCA
6 см
1B1C1- прямая призма,
∠АСВ
=90°,
АС=СВ, BN=NA,
точка N делит
AC=BC,
∠АВС=90°,
C
гипотенузу
∠CNC1= 45°,пополам.
СС1=6 см.
45°
ОтрезокVС1N составляет угол 45° с
A Найти:
плоскостью основания.
N
Боковое ребро равно 6 см.
Решение.
V= Sосн ·h
Найти объём призмы.
S ABC
1
a b
2
CN=CC1=6 cм
1
2
2
3
CN
V
(
6
2
)
6
6
6
216
см
CB
6 2см
2
cos 45
Ответ: 216 см3

12.

B1
C1
Основанием прямой призмы
является ромб, острый угол
A1
D1
ABCDA
1B1C1D1- прямая призма,
2 Дано:
которого
60°.
ABCD – ромб, ∠ВАD=60°, BB1=2,
Боковое ребро равно 2.
B
C ∠B1DВ= 45°.
45°
Найти: V диагональ призмы составляет
Меньшая
60°
с плоскостью основания угол 45°.
A
D
Найти объём призмы.
Решение.
V= Sосн ·h
S ABCD a b sin
∆ABD - равносторонний
AB=BD=2, т. к. ∆B1BD - равнобедренный
V 22 sin 60 2 4 3
Ответ:
4 3

13.

Что представляет собой
правильная шестиугольная
призма?
C1
B1
A1
F1
M1
B
C
D
A
M
F

14.

Какая диагональ в этой призме
наибольшая?
C1
B1
A1
1
DM1
2
DB1
3
DA1
F1
ПОДУМАЙ
!
ПОДУМАЙ
!
ВЕРНО!
M1
B
C
D
A
M
F

15.

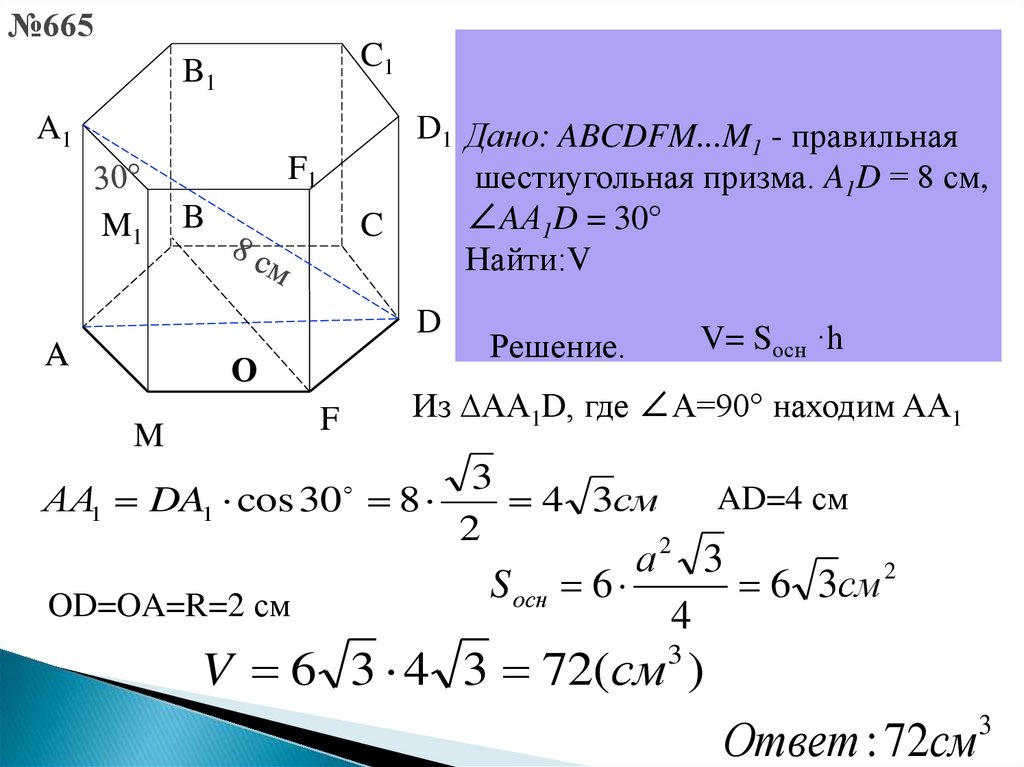
№665
C1
B1
Наибольшая диагональ
D1 Дано:
правильной
шестиугольной
ABCDFM...M
1 - правильная
призмы равна 8призма.
см
шестиугольная
A1D = 8 см,
∠AА
C
1D = 30° с боковым
и составляет
Найти:V
ребром угол в 30°.
A1
F1
M1
B
D
A
О
Из ∆AА1D, где ∠А=90° находим AА1
F
M
Найти
объём призмы.
V= Sосн ·h
Решение.
3
АA1 DA1 cos 30 8
4 3см
2
2
OD=OA=R=2 см
S осн 6
а
4
AD=4 см
3
6 3см 2
V 6 3 4 3 72(см )
3
Ответ : 72см
3

16.

Итог урока.
Ответить на вопросы:
а) Как вычисляется объем прямой призмы, основанием которой
является прямоугольный треугольник?
б) Как вычисляется объем правильной треугольной призмы?
в) Как вычисляется объем правильной четырехугольной призмы?

17.

Рефлексия
Я конечно не Ай-да я,
ленился, но и
ай-да
очень не
молодец!
трудился
Скажу
опять,
что я не
понял

18. Домашнее задание.

№659(а), №663(а, б), п.65

19.

Спасибо за
работу!