Похожие презентации:
Оптимальное обнаружение сигнала с полностью известными параметрами
1.
ОПТИМАЛЬНОЕ ОБНАРУЖЕНИЕСИГНАЛА С ПОЛНОСТЬЮ
ИЗВЕСТНЫМИ ПАРАМЕТРАМИ
2.
Дискретный сигналПринимаемый сигнал представляет смесь ожидаемого сигнала
S(t,α) с полностью известными параметрами и помехи:
U(t) n(t) S(t, )
Дискретные значения Uк, соответствующие этому колебанию,
удовлетворяют равенству:
U k n k Sk ,
где: Sk — известные величины (дискретные значения сигнала),
k= 1, 2,...
Дискретизация осуществляется в соответствии с теоремой
Котельникова:
1
t д
2 f макс
3.
Распределение шума и сигналаHаличие сигнала приводит к смещению распределения величины
Uk относительно распределения без сигнала Uk= nk:
Wсп U1 , U 2 , ... Wп U1 S1 , U 2 S2 , ...
Отношение правдоподобия для известного :
l U |
w п U1 S1 , U 2 S2 , ...
w п U1 , U 2 , ...
Отсчеты белого шума распределены по нормальному закону,
некоррелированны и статистически независимы, соответственно:
Wп U1 , U 2 , ... Wп U1 Wп U 2 ...
Wп U k
1
e
2 N 0 f макс
U 2k
2 N 0 f макс
t
e
N0
U 2k t
N0
,
N 0 f макс 2 – дисперсия квазибелого шума в полосе [0; f макс ]
4.
Отношение правдоподобияl U | e
1
N0
U2k t
k
e
2
N0
UkSk t
k
Осуществим предельный переход , fмакс→ , ∆t→0, получим:
lim S2k t
t 0 k
2
S
(t, ) dt E( ), – энергия ожидаемого сигнала
Запишем корреляционный интеграл:
lim U kSk t
t 0 k
S(t, ) U(t) dt
Окончательно отношение правдоподобия может быть
представлено в виде:
l U(t) | e E( )/ N0 e 2 z( )/ N0 , z( )
S(t, ) U(t) dt z U(t) |
5.
Алгоритм обнаружения известногосигнала
Отношение
правдоподобия
монотонная
функция
корреляционного интеграла для реализации U(t) и ожидаемого
сигнала с параметрами α.
Сравнение отношения правдоподобия с порогом l0 эквивалентно
сравнению корреляционного интеграла с соответствующим
порогом z0:
N0
1
z0 z0 ( )
ln l0 ( ) E( ),
2
2
где: N0 – спектральная плотность шума;
E(α) – энергия ожидаемого сигнала.
Алгоритм работы оптимального обнаружителя:
• вычислять корреляционный интеграл или его монотонную
функцию;
• сравнивать результат с порогом.
6.
Корреляционный обнаружитель• На
умножитель
подается
опорный
сигнал
Sоп(t,α),
соответствующий ожидаемому сигналу, и принятый сигнал U(t).
• Произведение интегрируется и дает оценку корреляционного
интеграла.
• Результат интегрирования сравнивается с порогом z0 порогового
устройства.
Уровень порога выбирается исходя из применяемого критерия
обычно требуют чтобы F была не больше допустимой.
Опорный сигнал соответствует по зондирующему, но с учетом
вектора параметров цели α (обычно учитывается время задержки и
частота смещения).
7.
Работа корреляционного обнаружителя8.
Распределения плотности вероятностивеличины корреляционного интеграла
9.
Задача многоканального обнаруженияПоложим, что сигнал принимается М-элементной антенной решеткой, элементы
которой расположены в одном или нескольких пунктах приема, тогда
совокупность всех принятых сигналов описывается вектор–столбцом U(t):
U(t) U 0 (t) U1 (t)
Реализация принимаемых колебаний:
U M 1 (t)
T
U i (t) A S(t, α, β) n(t, ν)
S(t, α, β) реализация сигнала
n(t, ν ) реализация помехи,
0 при наличии сигнала
A
1 при отсутствии сигнала
α – вектор информативных параметров сигнала (задержка, частота смещения,
угловые координаты источника излучения);
β – вектор неинформативных случайных параметров сигнала (начальная фаза,
амплитуда, совокупность случайных фаз и амплитуд, параметры случайной
поляризации сигнала);
ν – вектор случайных параметров помехи.
10.
Влияние дискретизации сигналаПосле дискретизации сигнала, получим L временных дискрет для
каждой функции Ui(t). Тогда общее число дискрет при Мканальном приеме i = 1, 2,…,М составит m = L·M, решение
принимается по M-мерному вектор-столбцу:
U U0
U1
U M 1
T
Сигнал обозначим вектором S = ||Si||, размерность которого
определяется общим числом временных дискрет во всех антенных
каналах:
U A S n
Помеху обозначим вектор-столбцом n = ||ni|| случайных значений.
Мат. ожидание каждого из них равно нулю: M{ni} = 0.
Мат. ожидание n также равно нулю: M{n} = 0, а его элементы
распределены по гауссовскому (нормальному) закону:
n2
w(n)
exp
2
2
2 2
1
11.
Учет нестационарных помехПомеха в общем случае считается нестационарной: различные
элементы выборки ni и nk помехи могут иметь различные
дисперсии σi и быть взаимозависимы, так что их центрированный
корреляционный момент, называемый ковариацией в общем
случае не равен нулю:
ik M
n M n M n n 0
2
i
k
Степень
взаимной
корреляции
характеризуют
обычно
коэффициентом корреляции элементов помеховой выборки
ik
M ni nk
i k
Величина ρik изменяется от +1 до -1.
Значения ρik равны ±1, когда величины ni и nk пропорциональны.
Знак плюс соответствует положительному, а знак минус —
отрицательному коэффициенту пропорциональности.
12.
Ковариационная матрица помехСовокупность корреляционных моментов (ковариаций) элементов
помеховой выборки образует прямоугольную корреляционную или
ковариационную матрицу в зависимости от смещенности или
неспещенности случайных процессов:
C ik ik i k
Диагональными элементами корреляционной матрицы оказываются
дисперсии элементов выборки: ψii = σi2.
Для ковариационной матриы можно найти определитель и матрицу,
соответственно
можно
найти
плотность
вероятности
эквивалентного гауссовского закона распределения помехового
вектор-столбца n с учетом компенсации ковариации помех:
W(n) 2
m/2
Wп (U) 2
C
m/2
1/2
C
exp n T C 1 n / 2
1/2
exp U T C 1 U / 2
13.
Примеры ковариационных матриц1. Если выборка состоит всего из одного дискрета, корреляционная
матрица вырождается: она содержит всего один элемент σ2, а ее
определитель |φ| = σ2.
Обратная матрица φ-1 также сводится к одному элементу 1/σ2, а
произведение φ·φ-1 – к одноэлементной единичной матрице.
При наличии одной помехи из общего соотношения приходим,
таким образом, к выражению wп и wсп , приведенными выше.
2. Получим плотности вероятности Wп(U) и Wсп(U) для случая,
когда выборка состоит из двух дискрет.
Корреляционная матрица С в данном случае имеет вид:
C
12
1 2
1 2
2
2
,
1/ 12
1
C 2 (1 ), C
2
1 / 1 2
2
1
2
2
1
/ 1 2
1/ 2 2
14.
Учет ковариации двух помехРаспределения вероятности в таком случае становятся двумерными
и имеют вид
U п (U1 , U 2 )
1
2 1 2 1
2
U12
U1 U 2 U 2 2
1
exp
2
2
2
2
1 2 2
2 (1 ) 1
Wcп (U1 , U 2 ) Wп (U1 S1 , U 2 S2 ),
что соответствует записи
w cп (U) w п (U S)
Полученные распределения показаны ниже с помощью линий
уровня для случаев:
0, 0,5
при 12 2 2 2
15.
Плотности распределения сигнала приналичии двух помех
16.
Алгоритмы оптимальногомногоканального обнаружения
Сводится к сравнению с порогом логарифма отношения
правдоподобия, так как логарифм линейное преобразование:
ln( l ) ln( wсп (y )) ln( wп (y ))
После подстановки
получим:
плотностей
распределения
вероятности
ln(l) (U T C 1S ST C 1U / 2) / 2 ST C 1S / 2
q
ln(l) q / 2 q н ,
2
U T C 1S ST C 1U н q
2
q 2 ST C 1S,
17.
Виды схем оптимальногомногоканального обнаружителя
С порогом обычно сравнивают:
ln(l) q
ln(l); ln(l) q / 2; н
.
q
2
2
они монотонно связаны с отношением правдоподобия и каждая из
них может использоваться для сравнения с соответствующим
порогом при двухальтернативном обнаружении.
Существует
несколько
вариантов
схемы
оптимального
обнаружителя.
В данном семействе схем подача на элемент схемы скалярной
величины показывается с помощью пунктирных стрелок, а
векторно-матричной величины с помощью сплошных стрелок
стрелок.
18.
Схема 1 оптимального обнаружителяПроводится два вида обработки m-элементного принятого U:
• линейное преобразование U к зависящему только от структуры
m2-элементной корреляционной матрицы помехи:
• выделение скалярной весовой суммы элементов с весовыми
коэффициентами, соответствующими составляющим полезного
сигнала и не зависящими от корреляционной матрицы помехи:
m
ST η Ci i , η C 1 U;
i 1
M П η U T C 1 M П U U T C 1 C I
M П η ηT C 1 M П U U T C 1 C C 1 C 1
19.
Схема 2 оптимального обнаружителяВ данной проводится m-элементная
коэффициентами ri вектора r = ||ri||:
весовая
обработка
с
m
U T r U i ri ; r C 1S
i 1
2 ST C 1 M п U U T C 1 S ST C 1 C C 1 S ST C 1 S q 2
Выходной уровень помехи в схемах 1 и 2 зависит от:
• входной корреляционной матрицы С
• вектора опорного/зондирующего сигнала S.
Уровень порога ξ0, обеспечивающий заданную условную
вероятность ложной тревоги F выбирается с учетом зависимости.
20.
Схема 3 оптимального обнаружителяЭто схема многоканального оптимального обнаружителя с
нормированным порогом.
Для оценки отношения правдоподобия здесь в виде весовый
коэффициенте используется нормированный вектор r.
Переход к нормированному весовому вектору rн учитывает
используемую в радиолокационных приемниках автоматическую
регулировку усиления по выходному уровню помехи.
rн r /q φ -1x / x T φ -1x
m
н yi rнi / q
i 1
н 2 M п н 2 M п 2 / q 2 1
21.
Параметр качества двухальтернативногообнаружения
Параметром обнаружения (квадратичным, линейным) называют
отношение сигнал-помеха на выходе линейного тракта обработки
(по мощности, по напряжению).
Отношение сигнал-помеха по мощности это отношение величины
квадрата математического ожидания весовой суммы ξ или ξн при
наличии сигнала и помехи к величине дисперсии этой же самой
весовой суммы (которая полагается постоянной вне зависимости
от наличия или отсутствия сигнала).
Параметры обнаружения приведенных выше оптимальных
обнаружителей одинаковы при одинаковых условиях на входе.
Расчет проведем для схемы 1 при наличии сигнала
M сп U S
M сп н M сп U T r / q ST C-1 S / q q 2 / q q
22.
Плотности распределения параметрадвухальтернативного обнаружения
Если нормировать дисперсию помехи, квадратичный параметр
обнаружения будет равен q2, а линейный q.
Для параметра обнаружения справедливы следующие выражения:
q 2 ST C-1 S ST r r T S;
q ST rн rн T S M сп н
Весовая сумма ζн или ζ есть линейная комбинация нормально
распределенных величин Ui и за счет закона больших чисел также
распределена по нормальному закону.
Так как Mсп{ζн}=q, M{(ζн-q)2}=1, плотности вероятности
нормированной весовой суммы имеют вид:
1
1
- н 2 /2
-( н q) 2 /2
w п ( н )
e
; w cп ( н )
e
2
2
23.
Кривые плотностей вероятности иуровень порога
Заштрихованные области, соответствуют интегралам от указанных
плотностей вероятности в области ζн >ζ0н и определяют условные
вероятности ложной тревоги F и правильного обнаружения D.
При интегрировании используют табулированные для ζ0н≥ 0
значения интеграла вероятности:
0н 2 / 2
e
0н
0
2 /2
d , 1
24.
Модифицированный интеграл Эрфанга(интеграл вероятности)
Для использования необходимо
определить интеграл вероятности
для ζ0н <0, так как функция обладает
свойством
Ψ(-ζ0н)=-Ψ(ζ0н),
зависимость Ψ(u) показана на
графике.
Если перейти к случаю когда сигнал
имеется получим:
он
e
он
q
2 / 2
d
e
2 / 2
d
q
e
2 / 2
d
25.
Кривые обнаруженияПри отсутствии сигнала положим q=0, с учетом Ψ(-∞)/2=-1/2,
выразим условные вероятности правильного обнаружения и
ложной тревоги:
D
он
p d
сп
н
н
0,5 0,5 q он ,
F
он
p d
п
н
н
0,5 0,5 он
Кривые обнаружения связывают
условную
вероятность
правильного обнаружения и
ложной
тревоги
и
фиксированный уровень порога
ζ0н. Для построения кривых
фиксируется
вероятность
ложной тревоги F = F0.
26.
Условия расчета параметровобнаружения в двухэлементной выборке
При расчете полагают что:
• отсутствует корреляция элементов выборки помехи;
• помеха стационарна во времени и пространстве;
• дисперсия помехи и собственных шумов за время наблюдения
постоянна.
Если в выборке имеется более двух элементов данные условия
могут быть не выполнены и соответственно требуется информация
для декорреляции входной выборки.
Двухэлементная выборка соответствует напряжениям двух
элементов антенной системы в один и тот же момент времени. Она
образована помехой либо наложением сигнала и помехи. Выборка
сигнала S известна. Известна также корреляционная матрица
помехи C и обратная ей матрица.
27.
Межэлементное нормирование поуровню помехи
Весовой вектор для структурной схемы 2:
2
x
/
1
1
1
r C 1 x
1 2 x1 / 1 2
x 2 / 1 2
x 2 / 2
2
r1
r2
Весовая сумма в таком случае имеет вид
U T r [ S1н S2н U1н S2н S1н U 2н ] / (1 2 )
[ U1н U 2н S1н U 2н U1н S2н ] / (1 2 )
Проведем оптимальное межэлементное взвешивание для
устранения не стационарности помехи:
U1н U1 / 1 , U 2н U 2 / 2 , S1н S1 / 1 ,S2н S2 / 2
Тогда параметр обнаружения q определяется выражением:
q 2 ST r
1
2
2
S
S
1н
2н 2 S1н S2н
2
1
28.
Обнаружение и независимыестационарные помехи
Коэффициент корреляции выборки ρ=0, дисперсии
элементов выборки равны σ12= σ22 =σ2, соответственно:
U1н S1н U 2н S2н , q 2 S1н 2 S2н 2
Каждое из принятых нормированных напряжений U1н, U2н
умножается на соответствующее нормированное по уровню
помехи значение ожидаемого напряжения. Если математическое
ожидание ζ в отсутствие сигнала равно нулю Mп{ζн}=0, то при его
наличии оно равно:
M cп S1н 2 S2н 2 q 2 q12 q 2 2
где |S1н|=q1, |S2н|=q2 – параметры обнаружения элементов выборки.
Накопление сигнала осуществляется независимо от знака элементов
выборки сигнала с одинаковыми весами элементов выборки, так как
дисперсии помехи равны.
29.
Обнаружение и нестационарные помехи1. Коэффициент корреляции выборки ρ=0, дисперсии элементов выборки
не равны σ12≠ σ22, соответственно
когерентное накопление сигнальных
составляющих производится с различными весами:
S1н S1 / 1 ,S2н S2 / 2
Весовая обработка связана с межэлементным нормированием
принимаемых напряжений по ожидаемому уровню помехи. С меньшим
весом учитывается элемент выборки, принимаемый на фоне более
интенсивной помехи.
2. Коэффициент корреляции выборки ρ ≠ 0, дисперсии
элементов выборки не равны σ12≠ σ22, когерентное накопление сигнальных
составляющих с учетом когерентной компенсации:
U '1н U1н U 2н , U '2н U 2н U1н
Компенсации коррелированных частей помехи предшествует
межэлементное нормирование принимаемых колебаний, обеспечивающее
выравнивание помех по интенсивности:
y1н y1 / 1 , y2н y2 / 2
30.
Обнаружение при значительнойкорреляции помех
Для сильно коррелированной помехи роль компенсации может
оказаться значительнее роли корреляционного накопления.
Обработка неэффективна, если
x1н x 2н , 1, x1н x 2н 0,
т. е. когда отсутствуют существенные различия между сигналом и
помехой. В этом случае: q2=q12 и использование второго дискрета
не изменяет параметр обнаружения.
Полезный сигнал компенсируется при его использовании вместе с
помехой, помеха накапливается, как и полезный сигнал,
компенсация, и накопление оказываются неэффективными.
31.
Многоканальный корреляционныйобнаружитель непрерывного сигнала с
известными параметрами на фоне
гауссовской коррелированной помехи
32.
Обнаружение непрерывного сигналаПри переходе от дискретных величин к непрерывным выражения
для весового интеграла и параметра обнаружения принимают вид:
U T (t) r (t)dt, q 2
T
2
S
(t)
r
(t)dtЭ
(t)
x
(t)
уд
А для определения весового вектора r(α) необходимо решить
интегрально-матричное уравнение:
С(t, ) r( )d S(t)
C(t,α) - матрица взаимных корреляционных функций канальных
помеховых напряжений является ядром уравнения;
S(t) – опорный сигнал.
С помощью вектора r(s) можно:
- синтезировать схему обработки, преобразуя rн(s)= r(s)/q можно
построить схему обнаружителя с заданной вероятностью ложной
тревоги F0;
- определять параметр обнаружения q.
33.
Структурные схемы обнаружителейнепрерывного сигнала с полностью
известными параметрами
34.
Одноканальное обнаружениенепрерывного сигнала
При одноканальном приеме М=1, а помеха - стационарный
шумовой процесс с постоянной спектральной плотностью
мощности N0 в неограниченной полосе частот (белый шум). По
теореме Хинчина корреляционная функция шума с точностью до
множителя сводится к дельта-функции:
φ(t , s ) N ( f ) cos 2 f (t s ) df
0
N0
(t s )
2
Подставляя С(t,s)в интегрально-матричное уравнение, получим в
силу фильтрующего свойства дельта-функции:
N0
(t )r( )d x(t)
2 0
r(t) 2 S(t) / N 0
35.
Выбор порога для одноканальногообнаружения
Оптимальная обработка сводится к вычислению и сравнению с
порогом нормированного или ненормированного весового
интеграла:
н / q, 2 z / N 0 ,
z
U(t) S(t)dt
Параметр обнаружения q2 сигнала на фоне белого шума равен
отношению удвоенной энергии сигнала к спектральной плотности
мощности шума:
2
q
E, E S2 (t)dt
N0
2
36.
Независимое двухканальноеобнаружение непрерывного сигнала
В двух каналах приема (М = 2) действуют некоррелированные
стационарные независимые белые шумы со спектральными
плотностями N01 и N02. Матрица корреляционных функций имеет
вид
N 01
1
C(t, ) (t )
0
2
0
N 02
Подставляя ее в интегрально-матричное уравнение, получаем
следующую систему двух интегральных уравнений:
N 01
(t ) r1 ( )d S1 (t),
2 0
N
02 (t ) r ( )d S (t)
2
2
2
0
r1 (t) 2 S1 (t) / N 01; r2 (t) 2 S2 (t) / N 02
37.
Схема независимого двухканальногообнаружителя непрерывного сигнала
Оптимальная обработка сводится к суммированию нормированных
по уровню шумов корреляционных интегралов, а q2 сводится к
сумме аналогичных параметров одноканального обнаружения:
2 Э1 2 Э 2
2
2
y1 (t) x1 (t)dt
y 2 (t) x 2 (t)dt; q 2
q12 q 2 2
N 01
N 02
N 01
N 02
38.
Двухканальное обнаружение прикоррелированных помехах
Каналы с коррелированными помехами встречаются:
- при использовании различных антенных элементов, принимающих колебания общих источников мешающих колебаний;
- при использовании незадержанных и задержанных на период
посылки мешающих колебаний в импульсном радиолокаторе с
селекцией движущихся целей.
Соответственно
в
каналах
имеются
коррелированные
стационарные помеховые колебания типа белого шума со
спектральными плотностями мощности N01 и N02.
Матрица корреляционных функций для рассматриваемых случаев
имеет вид
N 01
1
C(t, ) C (t ), C
2
N 01 N 02
N 01 N 02
N 02
39.
Алгоритм двухканального обнаруженияна фоне коррелированных помех
Подставим корреляционную матрицу в интегрально-матричное
уравнение, и решим его относительно весового вектора r(t) :
r (t) 2C 1S(t),
1
C
1/ N 01
/ N 01 N 02
/ N 01 N 02
1/ N 02
S1 (t) / N 01 S2 (t) / N 01 N 02
2
r (t)
2
1 S2 (t) / N 02 S1 (t) / N 01 N 02
2
2
2
2
q
[S
(t)
S
1н
2н (t) 2 S1н (t) S2н (t)]dt
2
1
U1н (t) U1 (t) / N 01 , U 2н (t) U 2 (t) / N 02
S1н (t) S1 (t) / N 01 , S2н (t) S2 (t) / N 02
40.
Схема двухканального обнаружителя нафоре коррелированных помех
Интегрирование соответствует непрерывному накоплению сигнала
во времени, в обнаружителе осуществляются следующие операции:
межканальное накопления полезного сигнала, межканальная
компенсация коррелированной части помех, межканального
нормирование.
41.
Обнаружение на фоне нестационарнойпомехи
Пусть Рассмотрим для одноканального обнаружение воздействие
нестационарной
дельта-коррелированный
шумовой
процесс
с
корреляционной функцией
N 0 (t)
C(t, )
(t )
2
N0(t) медленно меняющаяся во времени спектральная плотность
мощности шума.
Подставим С(t,α) в интегрально-матричное уравнение:
S(t) U(t)
r(t) 2S(t) / N 0 (t), 2
dt
N 0 (t)
q
2
q 0 (t)dt; q 0 (t)
2
2
2Е уд (t)
N 0 (t)
, E уд (t) S2 (t)
Таким образом алгоритм сводится к взвешиванию временных участков
сигнала, меньший вес у участков с большей долей помехи.
42.
Многоканальный корреляционныйобнаружитель комплексного сигнала с
полностью известными параметрами
43.
Комплексная модель узкополосноговысокочастотного колебания
Полоса узкополосного сигнала значительно меньше несущей
частоты f0. С учетом преселекции ограничены полосы помех
n(t)=||ni(t)|| и принимаемых колебаний S(t)=||Si(t)||.
a t am t cos 2 f 0 t t
Изменение амплитуды ат(t) и начальной фазы φ(t) за период 1/f0
несущей частоты невелики, в пределе их могут полагать
постоянными. Воспользовавшись формулами Эйлера после замены
переменных получим:
U t Re A t e j 2 f0 t A t e j 2 f0 t A* t e j 2 f0 t / 2
2 f 0 t t , cos Re e j e j e j / 2,
A t am t e
j t
A t am t e
j t
комплексная амплитуда высокочастотного колебания
сопряженная комплексная амплитуда
44.
Взаимное влияние пары колебанийa(t) представляет собой к действительную часть произведения
комплексной амплитуды А(t) и высокочастотного комплексного
множителя ej· 2π·f0 ·t или к полусумму аналогичных комплексносопряженных произведений.
Возьмем другое высокочастотное колебание b(t), взятое в какой-то
иной момент времени t2:
j 2 f 0 t2
j 2 f 0 t2
*
/ 2
b t2 B t2 e
B t2 e
Произведение a(t1)·b(t2) сведется к сумме функций разностного и
суммарного времен, по формуле Эйлера сведем функции одного
времени к реальной части, получим:
1
j 2 f 0 t1 t2
j 2 f 0 t1 t2
a t1 b t2 Re A t1 B* t2 e
A t B t2 e
2
45.
Приближенное вычисление интегралапроизведения колебаний
При t1 = t2 и медленно изменяющихся A(t) и В(t)
t 0 1 / f 0
t0
t 0 1 / f 0
j 4 f 0 t
A t B t e j 4 f 0 t dt A t0 B t0
e
dt 0
t0
При интегрировании за время t2 - t1,
существенно превышающее период
колебаний 1/f0, получаем:
t2
t
t2
t2
1 2
*
a
t
b
t
dt
Re
A
t
B
t 2 t t dt
1
1
1
t a t b t dt 2 Re t A* t B t dt
1
1
46.
Вычисление взаимной корреляционнойфункции случайных сигналов
1
1
j 2 f 0 t1 t2
j 2 f 0 t1 t2
M a t b t Re M A t1 B* t2 e
M A t1 B t 2 e
.
2
2
Случайными здесь могут быть амплитуды и начальные фазы
колебаний a(t1), b(t2), соответственно M[A(t)·B(t)]=0.
M[A(t)·B*(t)] может не быть равным нулю когда A(t) = В(t), а
случайные начальные фазы компенсируются, тогда:
C t1 ,t2 M a t b t Re M A t1 B* t2 / 2 e
j 2 f 0 t1 t2
.
Взаимная корреляционная функция С(t1, t2) двух колебаний a(t1) и
b(t2) определяется действительной компонентой взаимной
корреляционной функции их комплексных амплитуд с учетом
высокочастотного множителя.
47.
Комплексная корреляционная матрицапомехи
Если принимается сигнал U(t) = ||Ui(t)||, тогда мгновенное значение
в соответствующих каналах:
ui t Re U i t e j 2 f0 t
Взаимные корреляционные функции комплексных
помеховых напряжений в паре каналов имеют вид:
амплитуд
*
Cik t1 ,t2 M п U i t1 U k t2 / 2
Совокупность этих функций образует комплексную матрицу
помеховых взаимных корреляционных функций (комплексную
корреляционную матрицу помехи):
C t1 ,t2 Cik t1 ,t2 M п U t1 U * T t2 / 2 ,
U(t)=||Ni(t)||=N(t) – комплексные амплитуды помех.
48.
Свойства корреляционной матрицыпомехи
Комплексная корреляционная матрица помехи С(t1,t2) при t1 = t2
оказывается эрмитовой:
Cki t1 ,t2 Cik t1 ,t2 ,C t1 ,t2 C t1 ,t2
*
T
*
При t1 ≠ t2 справедлива лишь обобщенная эрмитовость
комплексной корреляционной матрицы помехи: матрица переходит
в комплексно-сопряженную, если вместе с заменой номеров строк
и столбцов заменяются аргументы функций:
Cki t1 ,t2 Cik t2 ,t1 ,C t1 ,t2 C t2 ,t1
*
T
*
Весовая интегральная сумма при переходе к комплексной
скалярной записи принимает вид
M
1
1
*
Re U i t R i t dt Re Z, Z U T t R* t dt
2 i 1
2
49.
Комплексная запись основныхсоотношений обнаружения
Интегрально-матричное уравнение комплексного весового
вектора R(t) следует из уравнения вещественного весового
вектора r(t) и после преобразования получим:
1
C t1 , t 2 R t 2 dt 2 S t1
2
Выражение параметра обнаружения:
1
q Re ST t1 C* t1 dt1 ,
2
2
T
*
S
t
R
1 t 2 dt1 H
Проведя замены и подставив получим:
1
q 2 ST t R* t dt
2
50.
Схемы обнаружителя непрерывныхсигналов
Операция вычисления Re(Z) опущена, переход к нормированному
весовому вектору RH(t) = R(t)/q и к порогу ζ0н, определяемому
условной вероятностью ложной тревоги F.
51.
Алгоритмы многоканальногообнаружения сигналов
Дискретный
сигнал
Принимаемая
реализация
Сигнал
Корреляционная
матрица помехи
Весовая сумма
(интеграл)
Уравнение весового
вектора
Параметр обнаружения
Непрерывный
действительный
сигнал
U(t)=|Uk(t)|
Непрерывный
комплексный сигнал
U=|Uk|
Uk=A∙Sk+nk
Uk(t)=A∙Sk(t)+nk(t)
U(t)=|Uk(t)|
Uk(t)=A∙Sk(t)+nk(t)
S=|Sk|
S(t)=|Sk(t)|
S(t)=|Sk(t)|
C=||Ci,k||
C(t1,t2)=||Ci,k(t1,t2)||
C(t1,t2)=||Ci,k(t1,t2)||
ζ=UTr
ζ=∫UT(t)r(t)dt
ζ=Re(Z)
Z=0,5∙∫UT(t)R*(t)dt
C∙r=S
q2=ST∙r
∫C(t1,t2)r(t2)dt2=S(t1) 0,5∙∫C(t1,t2)R(t2)dt2=S(t1)
q2=∫ST(t)r(t)dt
q2=∫ST(t)R*(t)dt
52.
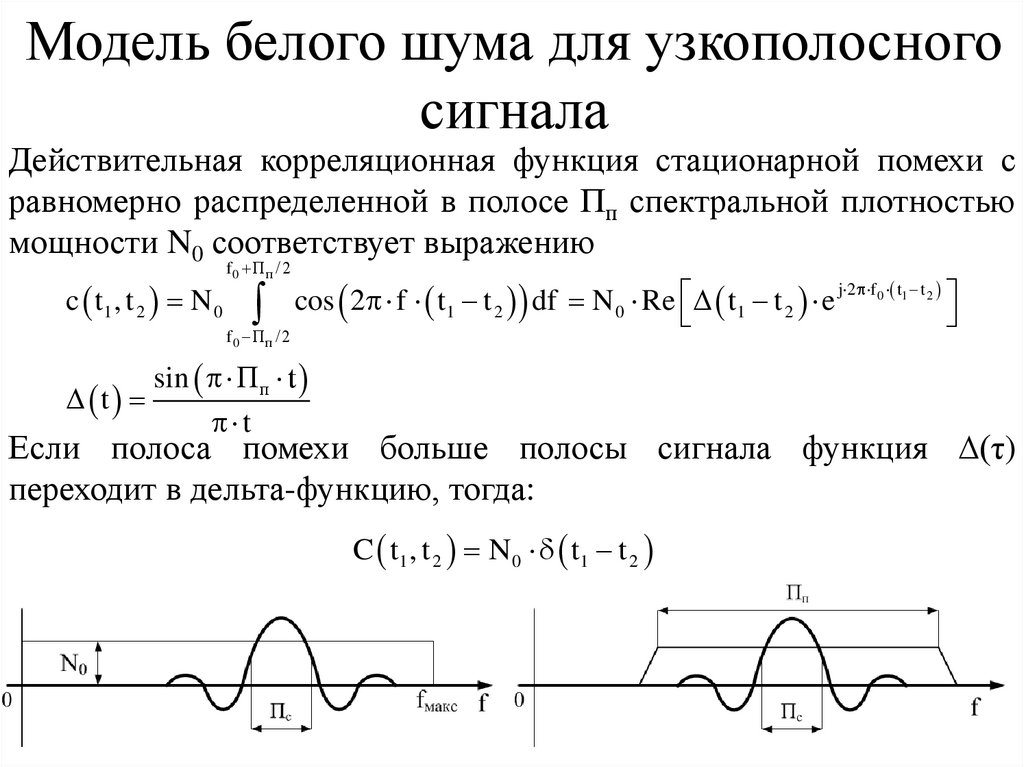
Модель белого шума для узкополосногосигнала
Действительная корреляционная функция стационарной помехи с
равномерно распределенной в полосе Пп спектральной плотностью
мощности N0 соответствует выражению
c t1 , t 2 N 0
f 0 П п /2
f 0 П п /2
t
j 2 f t t
cos 2 f t1 t 2 df N 0 Re t1 t 2 e 0 1 2
sin П п t
t
Если полоса помехи больше полосы сигнала функция ∆(τ)
переходит в дельта-функцию, тогда:
C t1 , t 2 N 0 t1 t 2
53.
Синтез многоканального обнаружителядля некоррелированных помех
Принимаемый сигнал на антенной решетке:
S t, S t S α , S α e j i
Вектор характеризует сдвиги фаз i (i=1, 2, ..., М), зависящие от
угловых координат источника сигнала.
Помеха не коррелирована по времени и элементам разрешения,
спектральная плотность мощности постоянная.
C t1 , t 2 N 0 I t 1 t 2 .
Весовой вектор будет иметь вид:
R t 2S t S α / N 0
До расчета весового интеграла следует провести пространственную
обработку:
M
U t Ui t e j i
i 1
54.
Алгоритм обработки сигнала ипоказатель обнаружения
Алгоритм расчете корреляционного интеграла ζ:
Re
U t S* t dt / N 0
Показатель обнаружения в таком случае:
1
2
T
*
q S α S α
N0
S t
2
dt 2M E 0 / N 0
M
M ei i e j i число элементов решетки
i 1
Е0
S t dt / 2 энергия сигнала.
2
Алгоритм может использоваться для квадратурного представления
сигнала без непосредственного представления сигнала в
комплексной форме.
55.
Схема многоканального обнаружителядля некоррелированных помех
56.
Синтез многоканального обнаружителяна фоне коррелированных помех
Комплексная корреляционная матрица помехи
С t1 , t 2
N 01 N 02
N 01
N 01 N 02
*
N 02
t1 t 2
C12 / N 01 N 02 комплексный коэффициент межканальной корреляции
Сигнал имеет вид:
S t
1
0
S t
Условия
соответствуют
приему
остронаправленной
и
слабонаправленной антеннами, соответственно принимаемым
слабонаправленной антенной сигналом можно пренебречь.
Аналогична ситуация при приеме различных поляризаций.
Система уравнений для комплексных весовых функций:
N 01 R1 t N 01 N 02 R 2 t 2S t ,
N 01 N 02 * R 1 t N 02 R 2 t 0
57.
Весовые коэффициенты и алгоритмработы обнаружителя
Решая систему уравнений получим весовые коэффициенты:
R1 t
2 X t
N 01 1
2
, R2 t
2 * X t
N 01 / N 02 1
2
Выражение весовой суммы ζ в таком случае:
U1 (t) N 01 / N 02 U 2 (t)
Re U t S t dt / N 0 , U (t)
2
1
*
Если ρ≠0 необходимо провести межканальную компенсацию:
U комп (t)
N 01 / N 02 U 2 t
1
2
Параметр обнаружения будет
иметь вид:
q
2
2
S(t) dt
N 01 1
2
2 E
N 01 1
2
























































 Физика
Физика








