Похожие презентации:
Многогранники. Теорема Эйлера
1. Тема: «Многогранники»
2. Что такое многогранник?
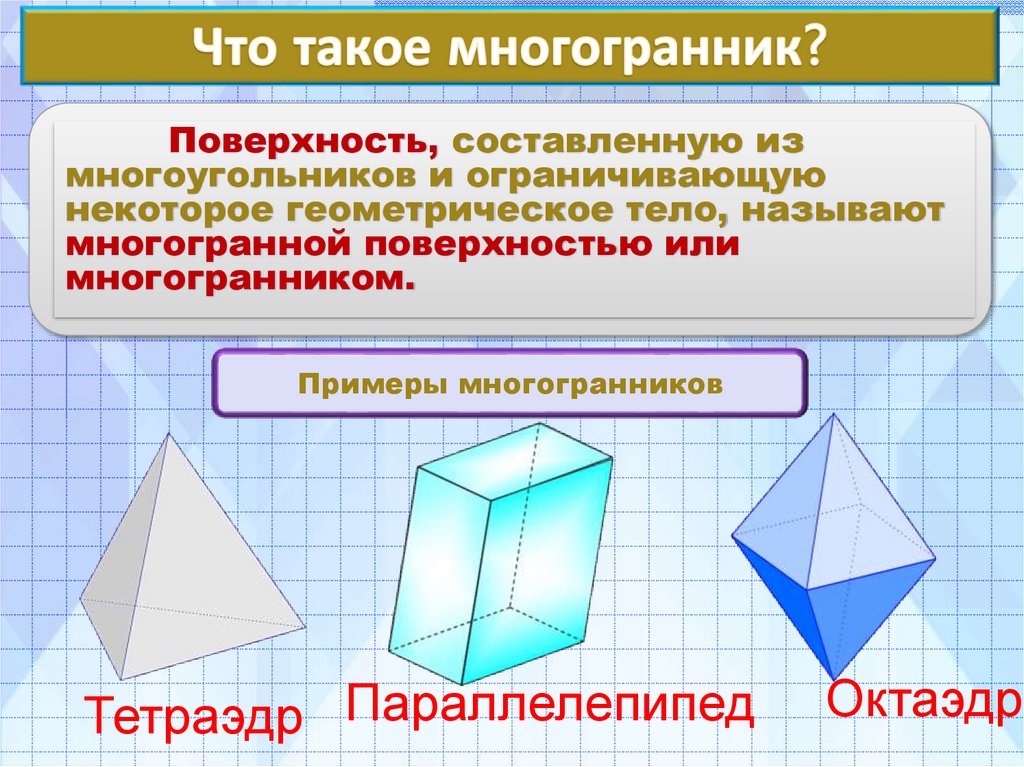
Поверхность, составленную измногоугольников и ограничивающую
некоторое геометрическое тело, называют
многогранной поверхностью или
многогранником.
Примеры многогранников
Тетраэдр Параллелепипед
Октаэдр
3.
многогранникиАлександри́ йский маяк (известен также как Фарóсский маяк) —
маяк на острове Фарос около египетского города Александрии, одно
из семи чудес света.
Был построен во время правления Птолемея II Филадельфа (280—247
году до н. э.). Высота маяка составляла порядка 120—150 метров. На
протяжении многих веков он был одним из самых высоких искусственных
сооружений в мире, а также входил в число трёх из Семи чудес
древности, сохранявшихся дольше всего.
4.
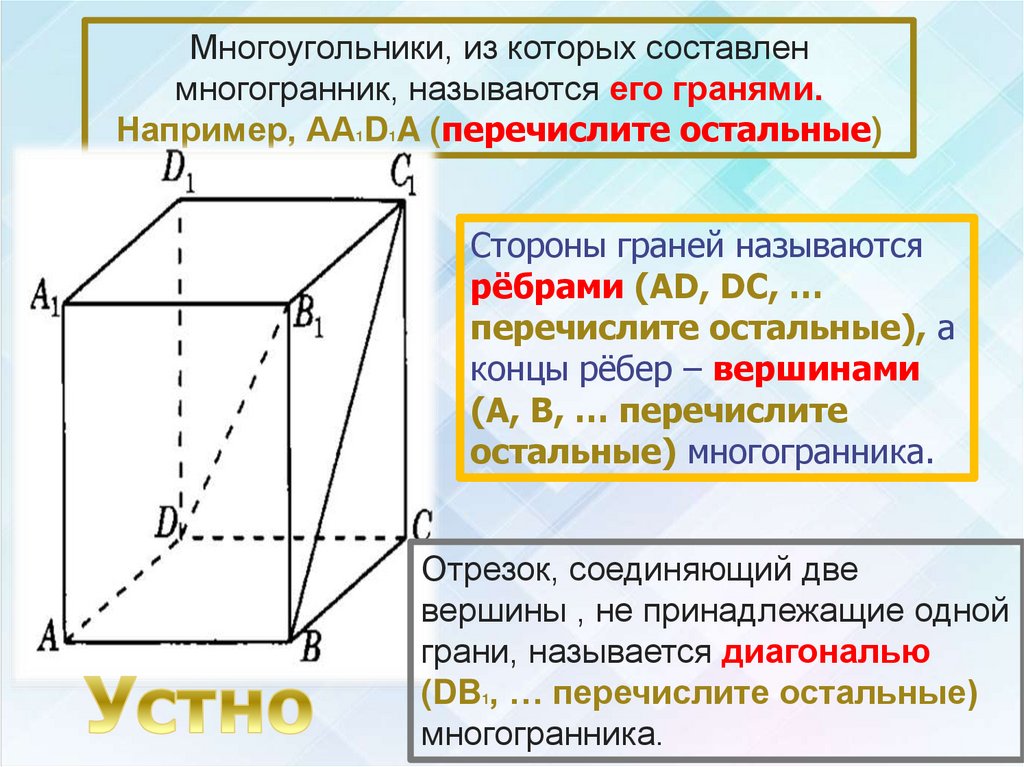
Многоугольники, из которых составленмногогранник, называются его гранями.
Например, АА1D1A (перечислите остальные)
Стороны граней называются
рёбрами (AD, DC, …
перечислите остальные), а
концы рёбер – вершинами
(А, В, … перечислите
остальные) многогранника.
Отрезок, соединяющий две
вершины , не принадлежащие одной
грани, называется диагональю
(DB1, … перечислите остальные)
многогранника.
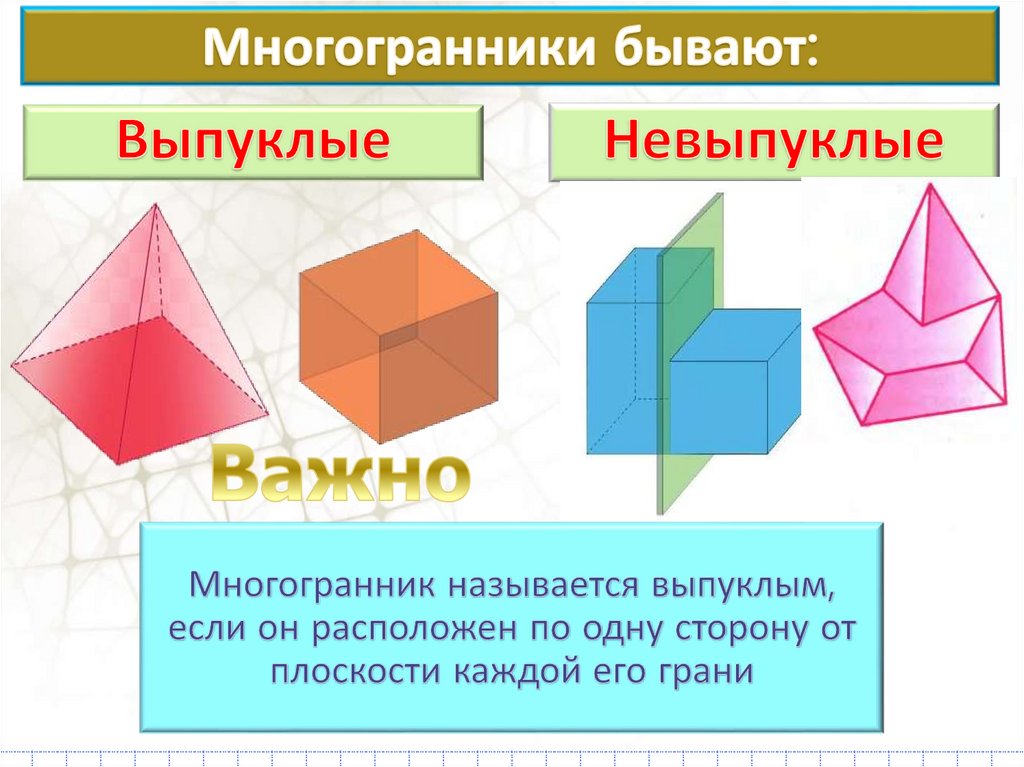
5. Многогранники бывают:
6. Теорема Эйлера:
В любом выпуклом многогранникесумма числа граней и числа вершин
больше числа рёбер на 2.
f + e – k =2
f- число граней;
е – число
вершин;
k – число рёбер.
Например, для
пирамиды (см. рисунок):
f = 5- число граней;
e = 5– число вершин;
k = 8– число рёбер.
Проверка:
5+5-8=2 -верно
7.
8. Призма
Многогранник, составленный из двухравных многоугольников,
расположенных в параллельных
плоскостях и n параллелограммов,
называется призмой.
9. Понятие призмы
Многогранник, составленный из двух равныхмногоугольников A1A2…An и B1B2…Bn, расположенных
в параллельных плоскостях, и n параллелограммов,
называется призмой
В5
В4
В1
В3
В2
A5
A4
A1
A3
A2
10.
11.
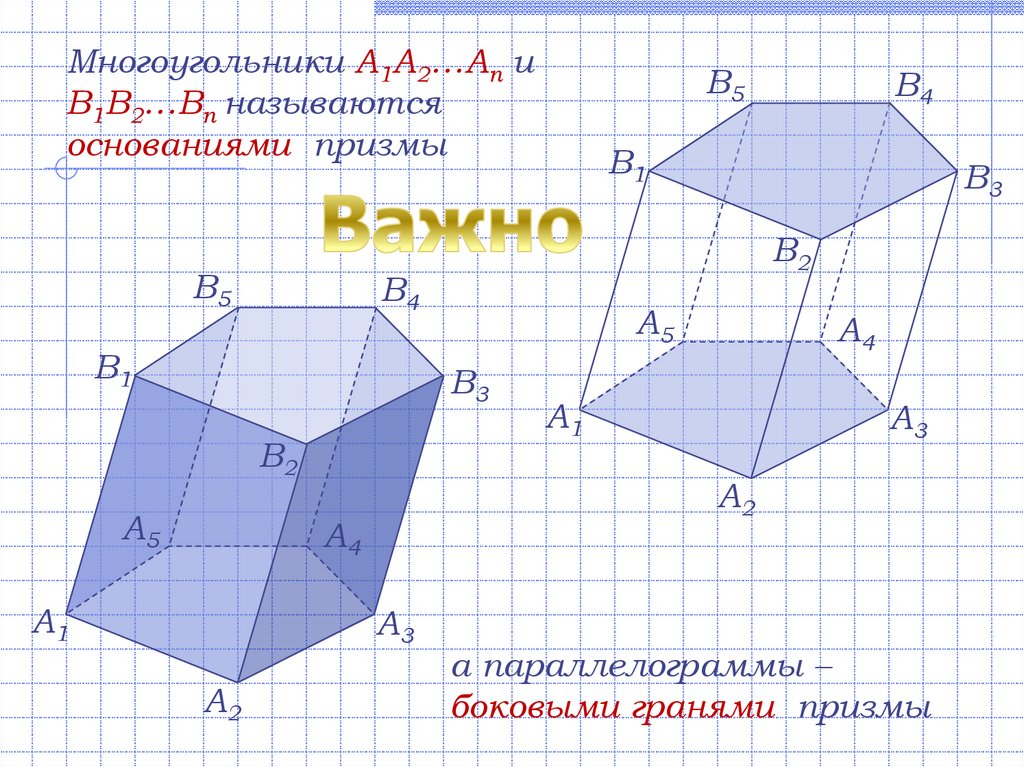
Многоугольники A1A2…An иB1B2…Bn называются
основаниями призмы
В5
A5
A3
A2
A4
A1
A3
A2
A4
A1
В3
В2
В3
В2
В4
В1
В4
В1
A5
В5
а параллелограммы –
боковыми гранями призмы
12.
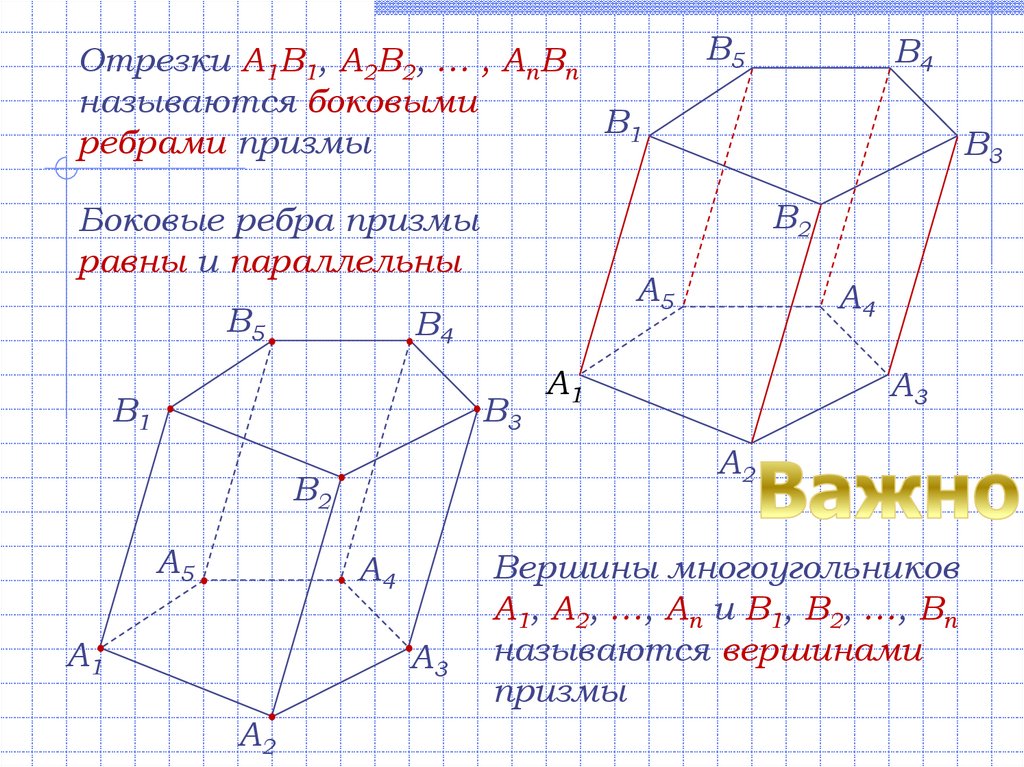
Отрезки A1B1, A2B2, … , AnBnназываются боковыми
В1
ребрами призмы
В3
A4
A1
A3
A2
A4
A1
A3
A2
В2
A5
В3
A5
В4
В1
В4
В2
Боковые ребра призмы
равны и параллельны
В5
В5
Вершины многоугольников
A1, A2, …, An и B1, B2, …, Bn
называются вершинами
призмы
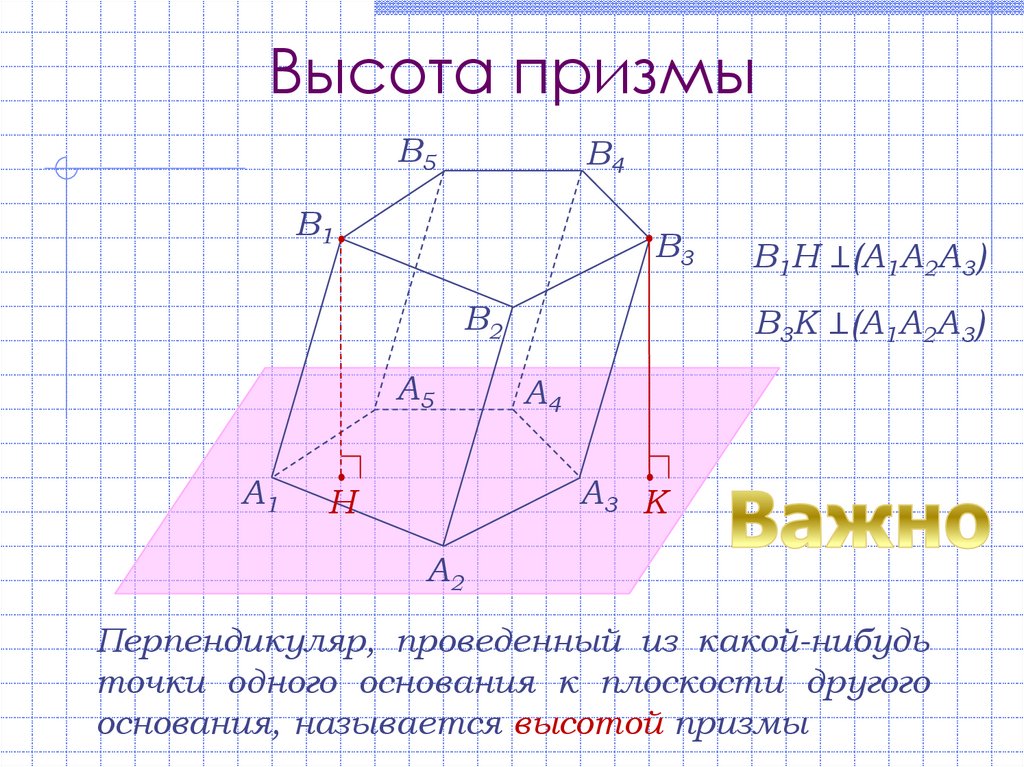
13. Высота призмы
В5В4
В1
В3
В2
A5
A1
В1Н ⊥(А1А2А3)
В3К ⊥(А1А2А3)
A4
A3 К
Н
A2
Перпендикуляр, проведенный из какой-нибудь
точки одного основания к плоскости другого
основания, называется высотой призмы
14.
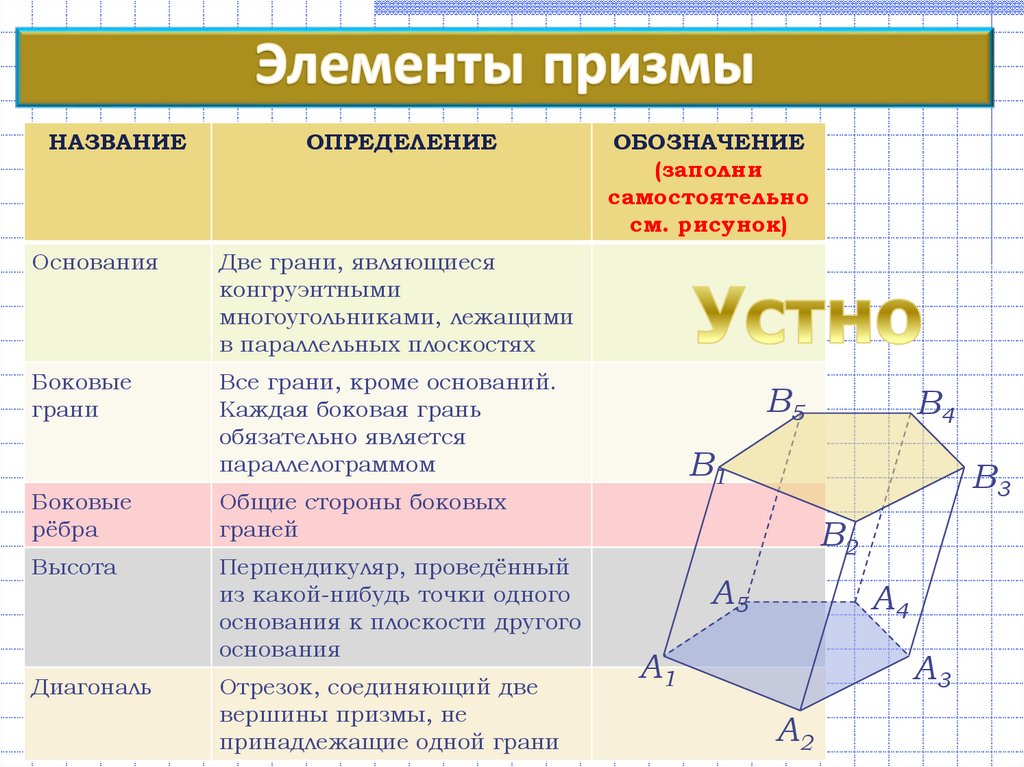
НАЗВАНИЕОПРЕДЕЛЕНИЕ
Основания
Две грани, являющиеся
конгруэнтными
многоугольниками, лежащими
в параллельных плоскостях
Боковые
грани
Все грани, кроме оснований.
Каждая боковая грань
обязательно является
параллелограммом
Боковые
рёбра
Общие стороны боковых
граней
Высота
Перпендикуляр, проведённый
из какой-нибудь точки одного
основания к плоскости другого
основания
Диагональ
Отрезок, соединяющий две
вершины призмы, не
принадлежащие одной грани
ОБОЗНАЧЕНИЕ
(заполни
самостоятельно
см. рисунок)
В5
В4
В1
В3
В2
A5
A4
A1
A3
A2
15.
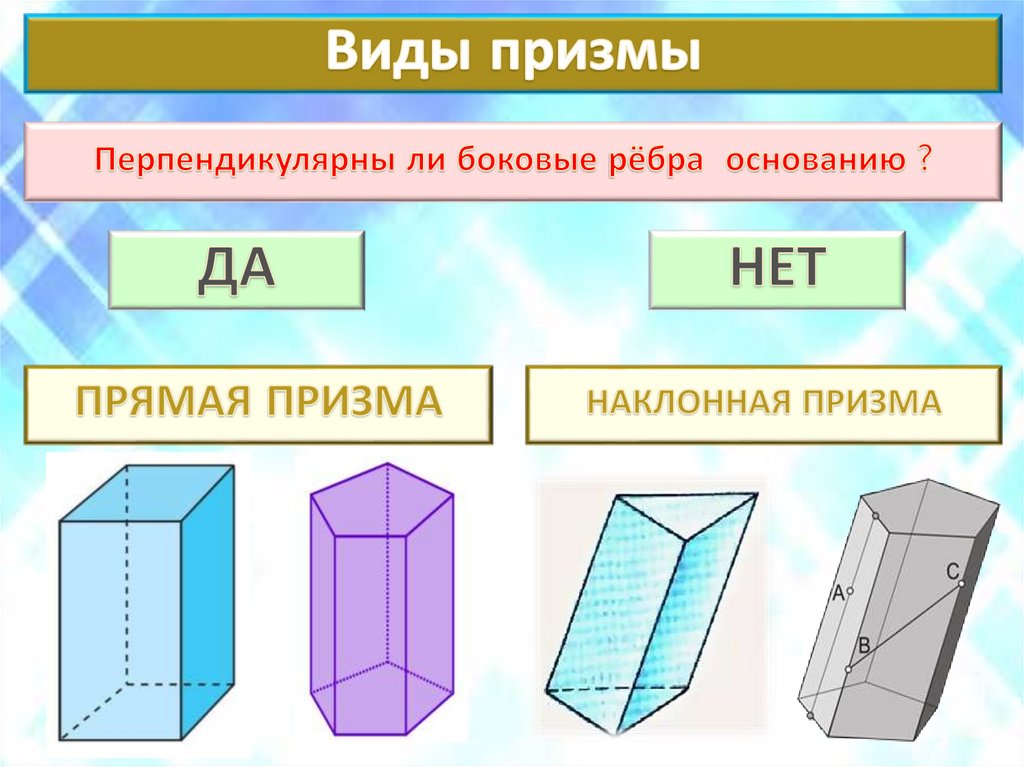
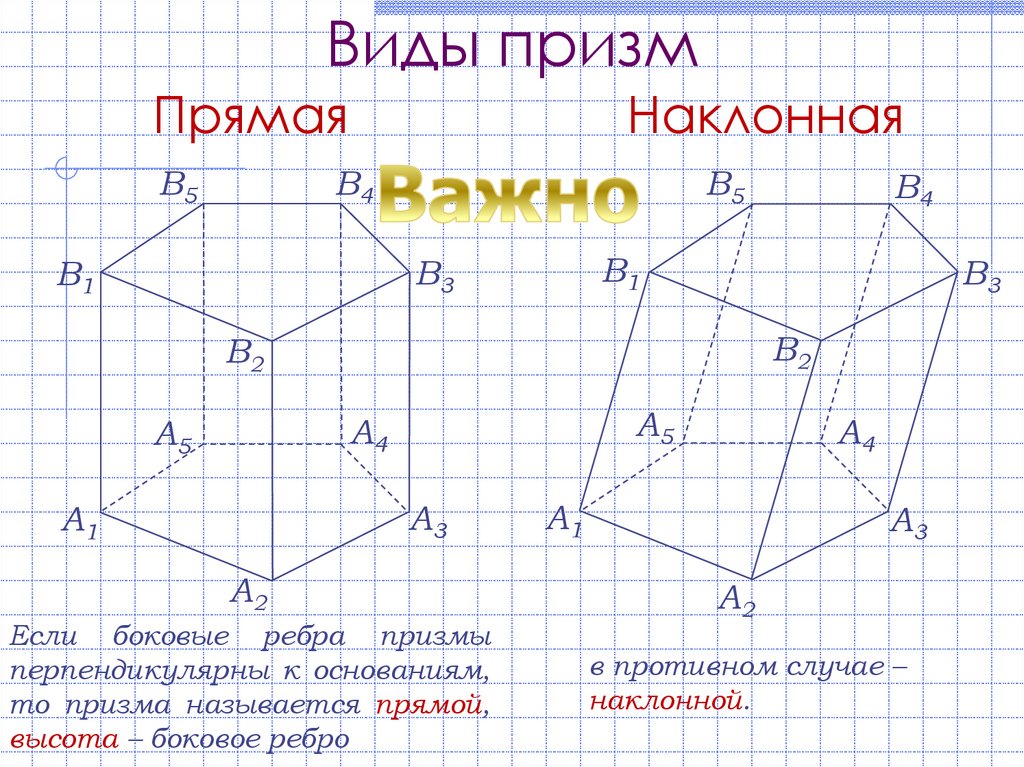
16. Виды призм
ПрямаяВ5
Наклонная
В4
В5
В1
В3
В1
В3
В2
В2
A5
A4
A5
A3
A1
В4
A2
Если боковые ребра призмы
перпендикулярны к основаниям,
то призма называется прямой,
высота – боковое ребро
A4
A1
A3
A2
в противном случае –
наклонной.
17. Правильные призмы
18. Правильная призма
В5В4
В3
В1
В2
A5
A1
A4
A3
A2
Прямая призма называется правильной, если её
основания – правильные многоугольники
У правильной призмы все боковые грани – равные
прямоугольники
19.
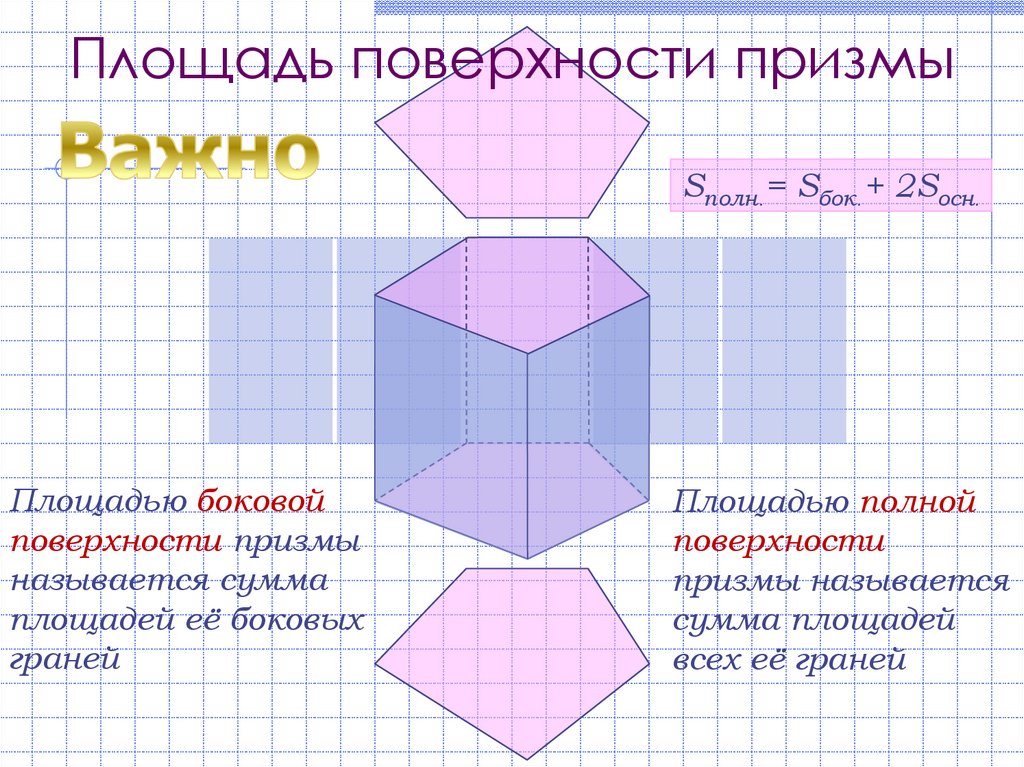
Площадь поверхности призмыSполн.= Sбок.+ 2Sосн.
Площадью боковой
поверхности призмы
называется сумма
площадей её боковых
граней
Площадью полной
поверхности
призмы называется
сумма площадей
всех её граней
20. Теорема о площади боковой поверхности прямой призмы
Площадь боковой поверхности прямой призмыравна произведению периметра основания на
высоту призмы
Sбок. = Росн.· h
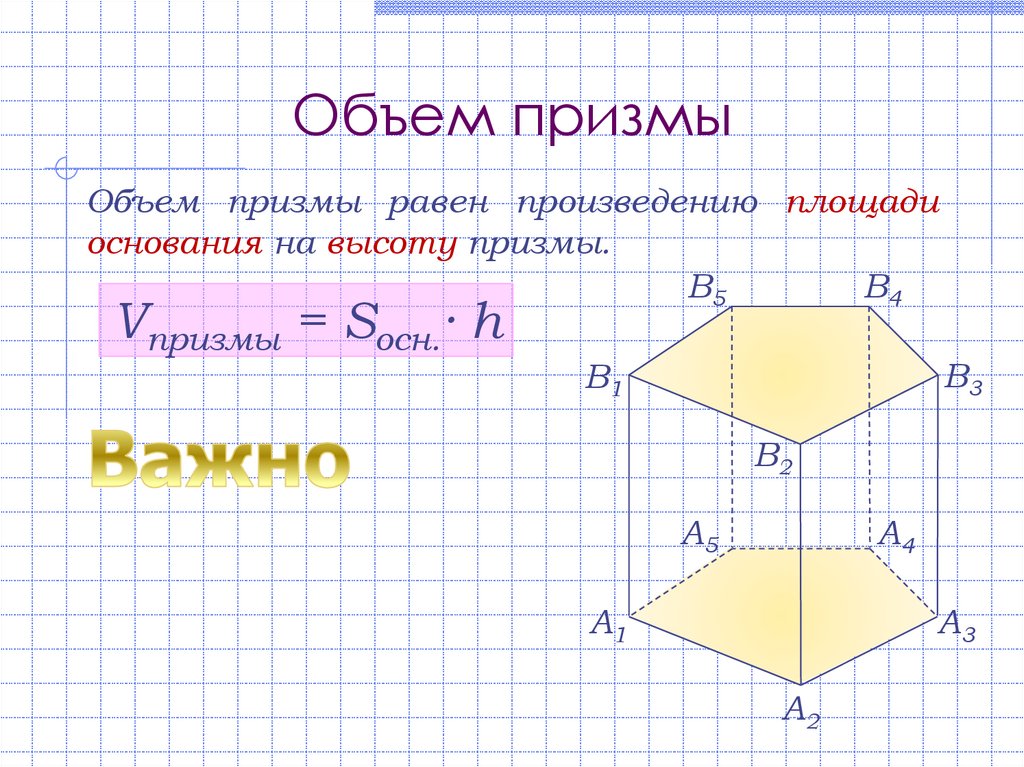
21. Объем призмы
Объем призмы равен произведению площадиоснования на высоту призмы.
В5
В4
Vпризмы = Sосн.· h
В3
В1
В2
A5
A4
A1
A3
A2
22.
В23.
В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты сосветом. Чтобы разложить свет на составляющие и получить спектр,
он использовал трехгранную стеклянную призму.
Ученый обнаружил, что, собрав раздробленный луч с помощью второй
призмы, можно опять получить белый свет. Так он доказал, что белый
свет является смесью разных цветов. Проходя через призму, световые
лучи преломляются.
24.
«Я затемнил мою комнату, − писал он, − и сделал очень маленькоеотверстие в ставне для пропуска солнечного света».
На пути солнечного луча ученый поставил особое трехгранное
стеклышко – призму. На противоположной стене он увидел
разноцветную полоску – спектр. Ньютон объяснил это тем, что призма
разложила белый цвет на составляющие его цвета. Ньютон первый
разгадал, что солнечный луч многоцветный.
25.
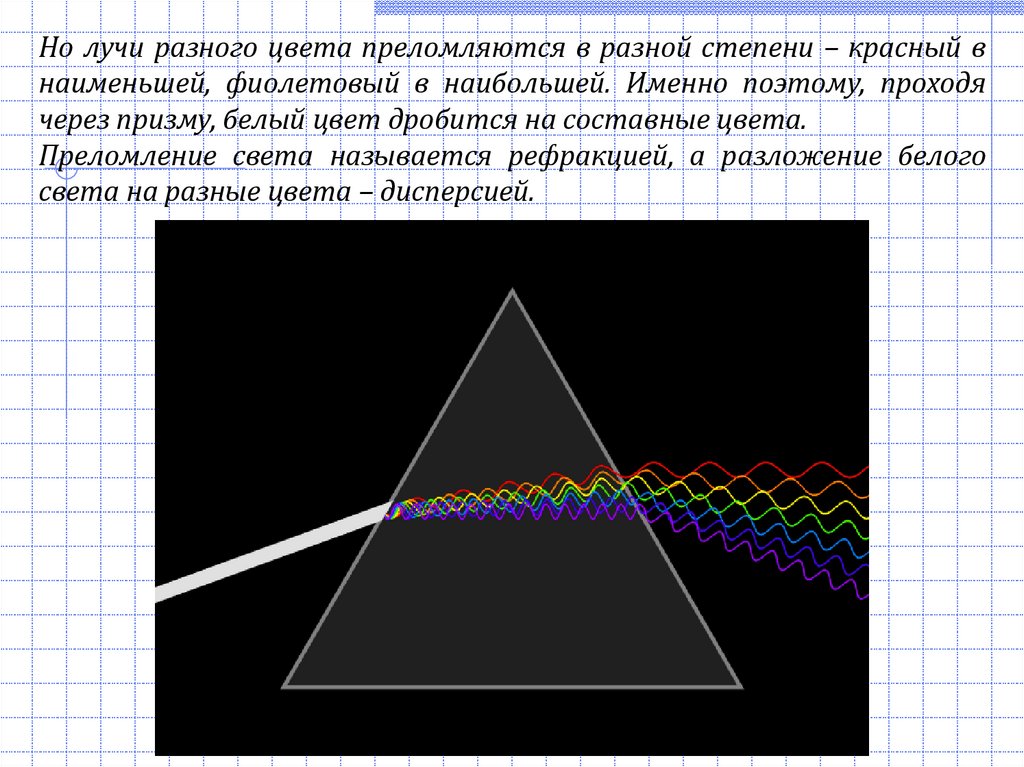
Но лучи разного цвета преломляются в разной степени – красный внаименьшей, фиолетовый в наибольшей. Именно поэтому, проходя
через призму, белый цвет дробится на составные цвета.
Преломление света называется рефракцией, а разложение белого
света на разные цвета – дисперсией.
26. Использование призмы для творческих фотоэффектов
27. Использование призмы для творческих фотоэффектов
28. Применение призм в лечении косоглазия
Принцип тренировки состоит в попеременном приставлении ктренируемым глазам на определенное время положительных
сферо – призматических элементов различной сферической и
призматической диоптрийности.
Графически это выглядит следующим образом:





















 Математика
Математика








