Призма

1.

ПРИЗМА
Выполнил: Габриелян Армен
ГРПОУ РО КТТ

2.

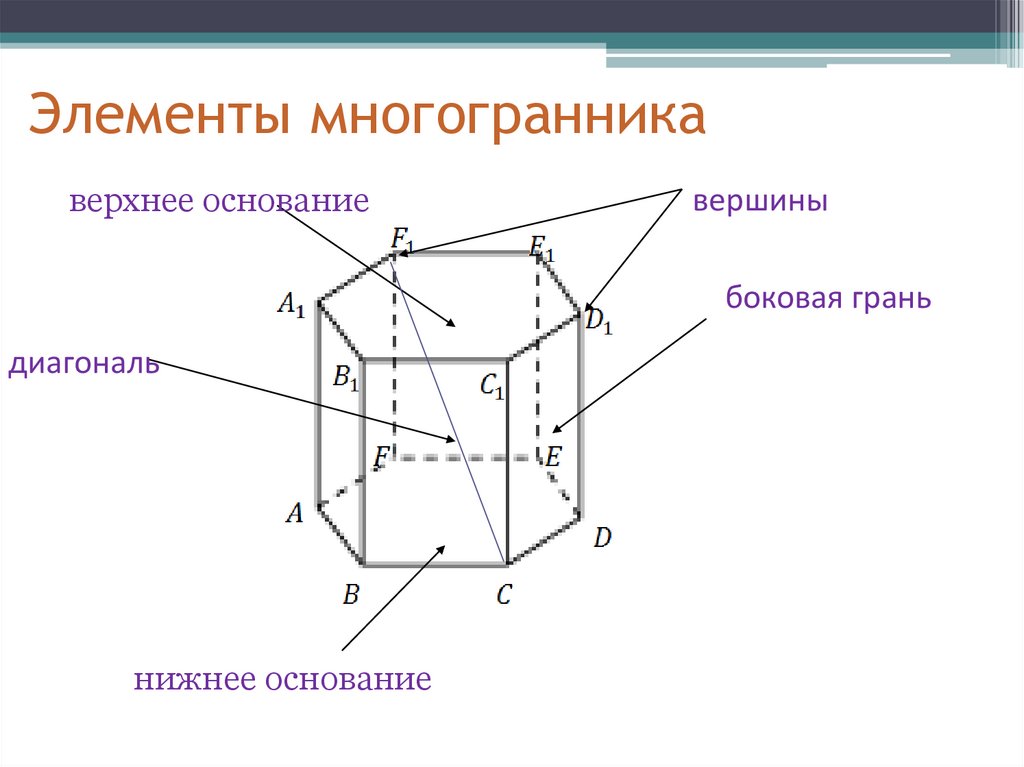
Элементы многогранника
верхнее основание
вершины
боковая грань
диагональ
нижнее основание

3.

Понятие призмы
Многогранник, составленный из двух равных многоугольников A1A2…An и
B1B2…Bn, расположенных в параллельных плоскостях, и n
параллелограммов, называется призмой
В5
В4
В1
В3
В2
A5
A4
A1
A3
A2

4.

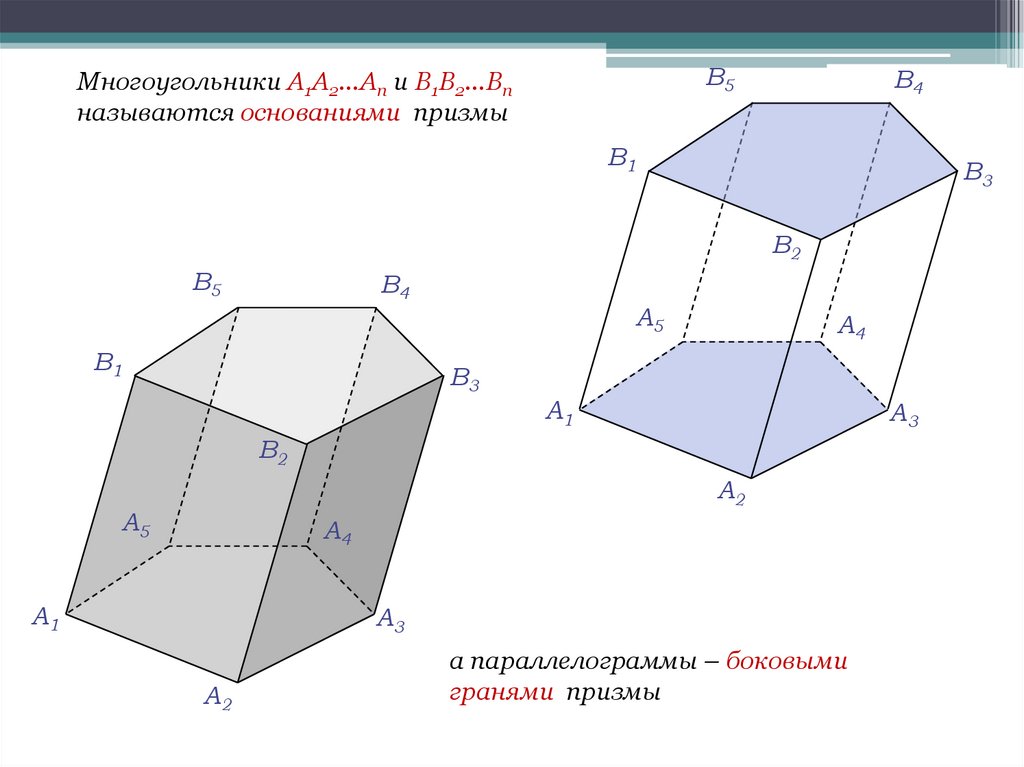
В5
Многоугольники A1A2…An и B1B2…Bn
называются основаниями призмы
В4
В1
В3
В2
В5
В4
В1
A5
В3
A4
A1
A3
В2
A2
A5
A4
A1
A3
A2
а параллелограммы – боковыми
гранями призмы

5.

В5
Отрезки A1B1, A2B2, … , AnBn называются
боковыми ребрами призмы
В1
В3
Боковые ребра призмы равны и
параллельны
В5
В2
A5
В4
В1
В3
A4
A1
A3
A2
A4
A1
A3
A2
В2
A5
В4
Вершины многоугольников A1, A2, …, An и
B1, B2, …, Bn называются вершинами
призмы

6.

Высота призмы
В5
В4
В1
В3
В2
A5
A1
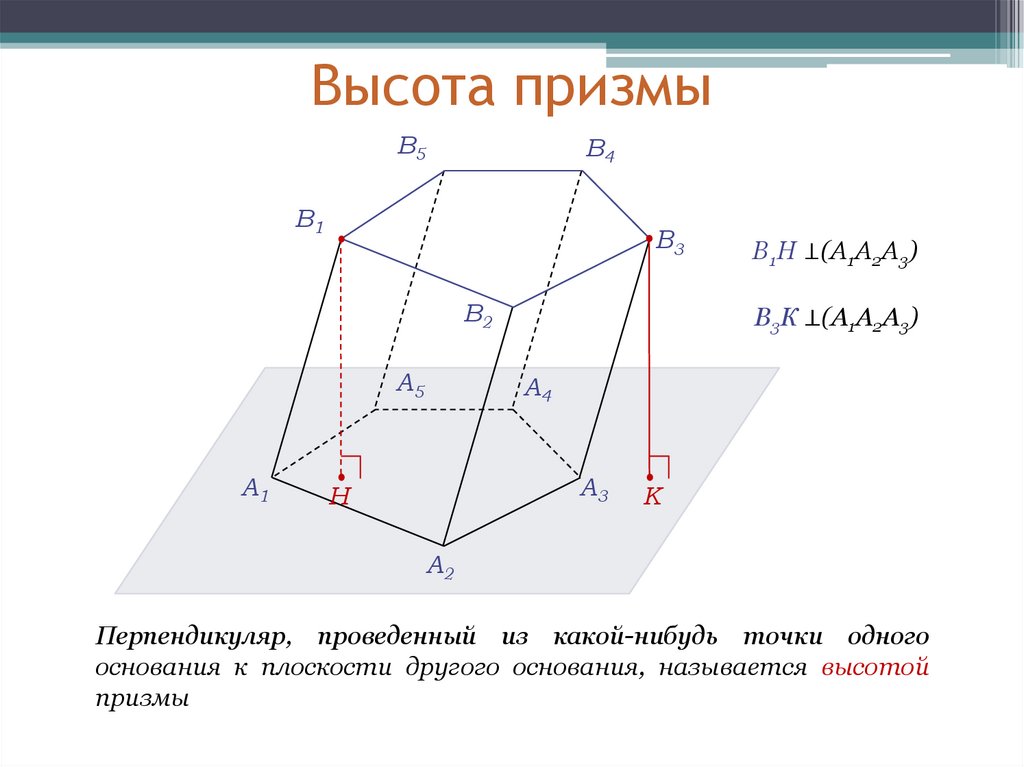
В1Н ⊥(А1А2А3)
В3К ⊥(А1А2А3)
A4
A3
Н
К
A2
Перпендикуляр, проведенный из какой-нибудь точки одного
основания к плоскости другого основания, называется высотой
призмы

7.

Виды призм
Прямая
Наклонная
В5
В4
В5
В1
В3
В1
В3
В2
В2
A5
A4
A5
A3
A1
В4
A4
A1
A3
A2
A2
Если боковые ребра призмы
перпендикулярны к основаниям,
то призма называется прямой,
высота – боковое ребро
в противном случае –
наклонной.

8.

Правильная призма
В5
В4
В3
В1
В2
A5
A4
A1
A3
A2
Прямая призма называется правильной, если её основания
правильные многоугольники
У правильной призмы все боковые грани – равные прямоугольники
–

9.

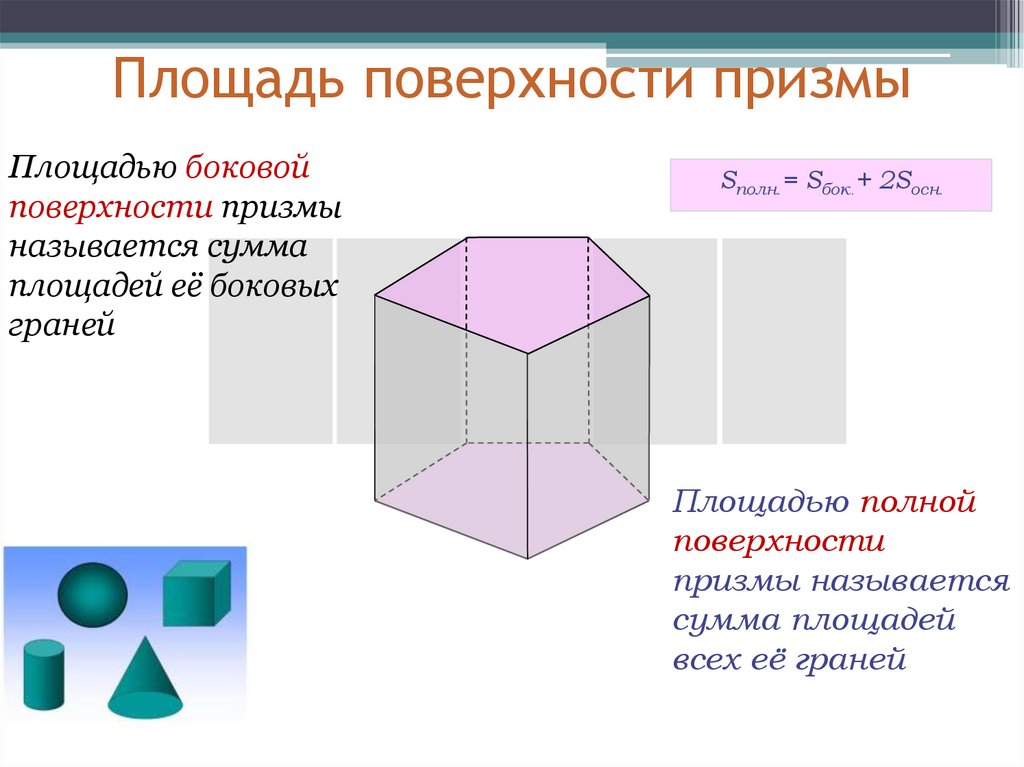
Площадь поверхности призмы
Площадью боковой
поверхности призмы
называется сумма
площадей её боковых
граней
Sполн.= Sбок.+ 2Sосн.
Площадью полной
поверхности
призмы называется
сумма площадей
всех её граней

10.

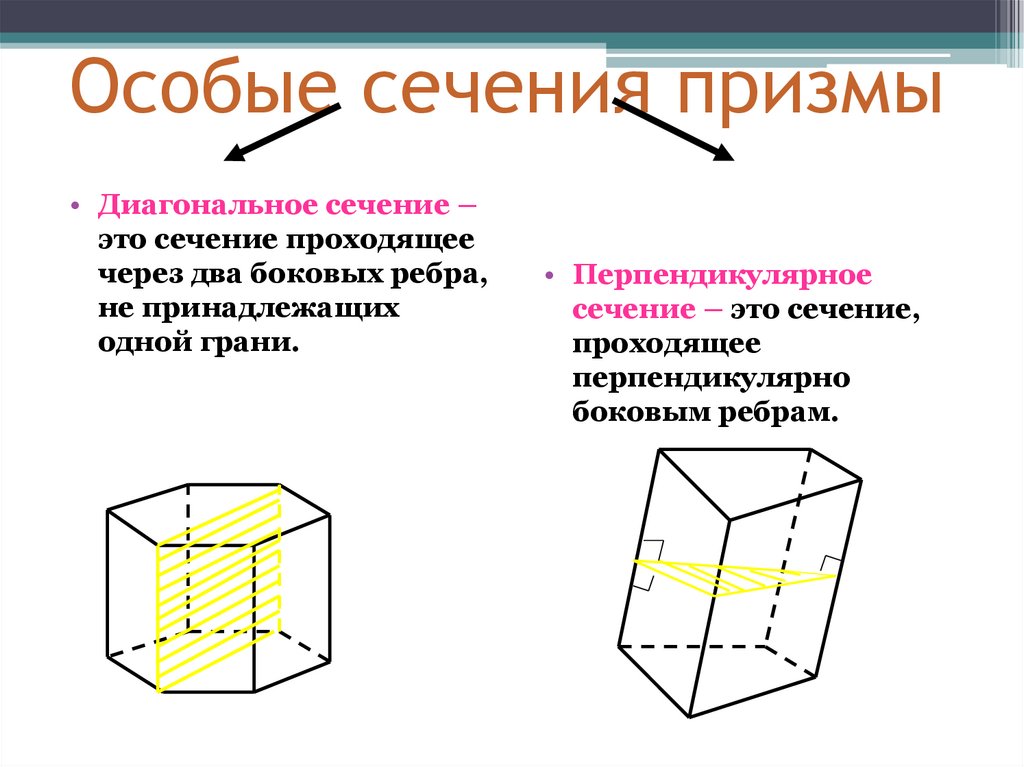
Особые сечения призмы
• Диагональное сечение –
это сечение проходящее
через два боковых ребра,
не принадлежащих
одной грани.
• Перпендикулярное
сечение – это сечение,
проходящее
перпендикулярно
боковым ребрам.

11.

Теорема о площади боковой поверхности
прямой призмы
Площадь боковой поверхности прямой призмы
равна произведению периметра основания на
высоту призмы
Sбок. = Росн.· h
Доказательство.
Боковые грани прямой призмы – прямоугольники, основания которых –
стороны основания призмы, а высоты равны высоте h призмы.
Sбок. = A1A2· h + A2A3· h + A3A4· h + … + An-1An· h =
= (A1A2 + A2A3 + A3A4 + … + An-1An) · h = Pосн.· h

12.

Теорема о площади боковой
поверхности наклонной призмы
Площадь боковой поверхности наклонной призмы равна
произведению периметра перпендикулярного сечения
и бокового ребра