Внутренняя норма рентабельности (IRR)

1.

Внутренняя
норма
рентабельности
(IRR)
1

2.

Внутренняя норма рентабельности (IRR)
IRR > i проект выгодный
Смысл: максимальная цена капитала,
при которой проект выгоден
2

3.

Как рассчитать IRR?
IRR > i проект выгодный
Смысл: максимальная цена капитала,
при которой проект выгоден
.

4.

Пример расчета
Внутренняя норма рентабельности (IRR)
0
1
2
3
4
-2500
850
900
800
750
.

5.

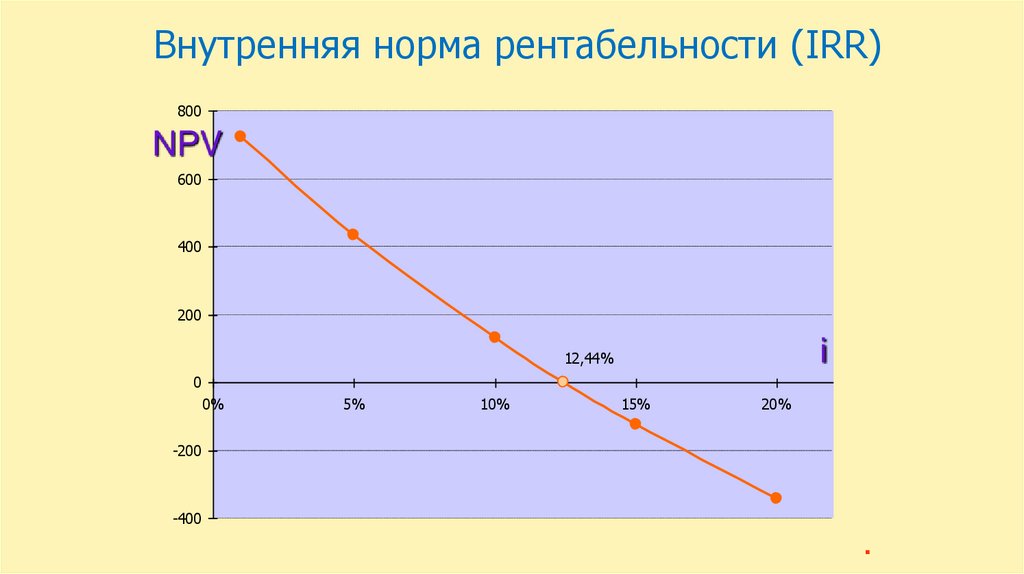
Внутренняя норма рентабельности (IRR)
800
NPV
600
400
200
i
12,44%
0
0%
5%
10%
15%
20%
-200
-400
.

6.

IRR= 12,44 %
При ставке дисконтирования 10 %
проект выгодный.
0
1
2
3
4
-2500
850
900
800
750
Если ставка стоимость финансирования
будет расти, как это повлияет на
эффективность проекта?
.

7.

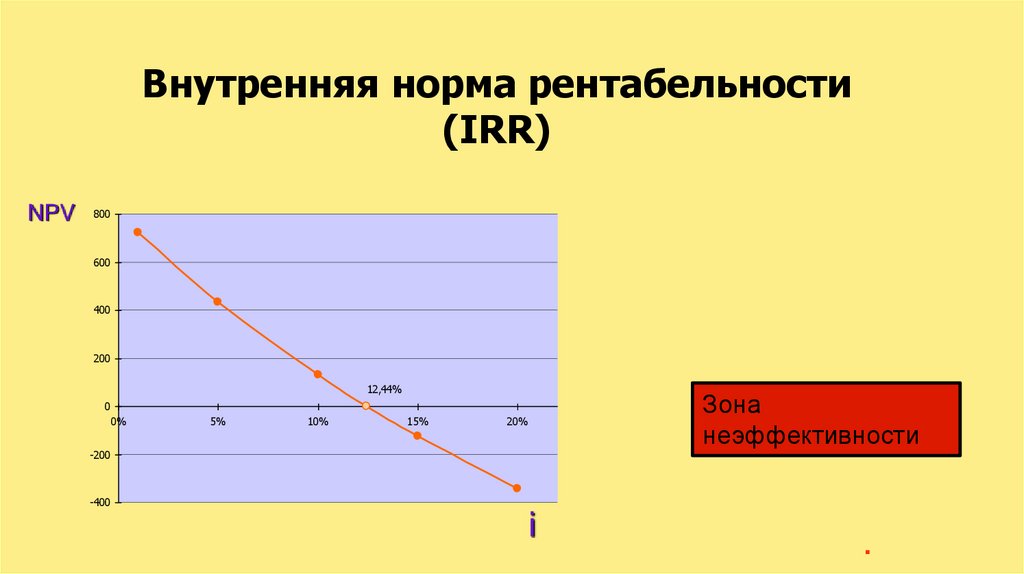
Внутренняя норма рентабельности
(IRR)
NPV
800
600
400
200
12,44%
Зона
неэффективности
0
0%
5%
10%
15%
20%
-200
-400
i
.

8.

Внутренняя норма рентабельности
(IRR)
0
-2500
1
1700
2
1000
3
200
4
100
приблизительно
точно
.

9.

Чем больше
внутренняя норма
рентабельности,
тем меньше его
эффективность
зависит от ставки
дисконтирования.
9

10.

Решаем задачи
10

11.

×
×
×
×
×
×
Найти внутреннюю норму рентабельности инвестиционного
проекта. Построить график зависимости NPV от ставки
дисконтирования.
0
1
2
3
4
-1500
500
700
1100
1300
Рассчитаем NPV при i=10 %.
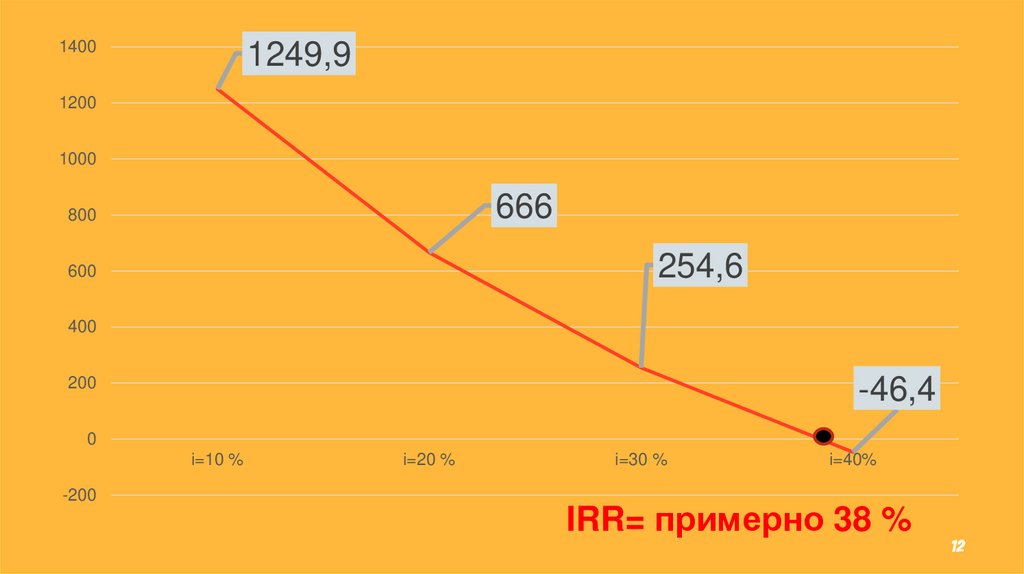
NPV= 1249,9 руб.
i=20 %, тогда NPV=666 руб.
i=30 %, тогда NPV=254 руб.
i=40 %, тогда NPV= -46,43 руб.
11

12.

1400
1249,9
1200
1000
666
800
254,6
600
400
-46,4
200
0
i=10 %
-200
i=20 %
i=30 %
i=40%
IRR= примерно 38 %
12

13.

×
×
×
×
×
×
Найти внутреннюю норму рентабельности инвестиционного
проекта. Построить график зависимости NPV от ставки
дисконтирования.
0
1
2
3
4
-1500
500
700
1100
1300
i=20 %, тогда NPV=666 руб.
i=30 %, тогда NPV=254 руб.
i=40 %, тогда NPV= -46,43 руб.
i=38 %, тогда NPV= 6,89 руб.
IRR=0,3+((254/(254+46,43))*(0,4-0,3)=0,3845
13

14.

×
×
×
IRR проекта равна примерно 38 %.
Проект прибыльный в случае, если ставка
дисконтирования будет меньше 38 %.
Чем больше разница между IRR и i , тем меньше
проект зависит от изменения ставки
дисконтирования.
14

15.

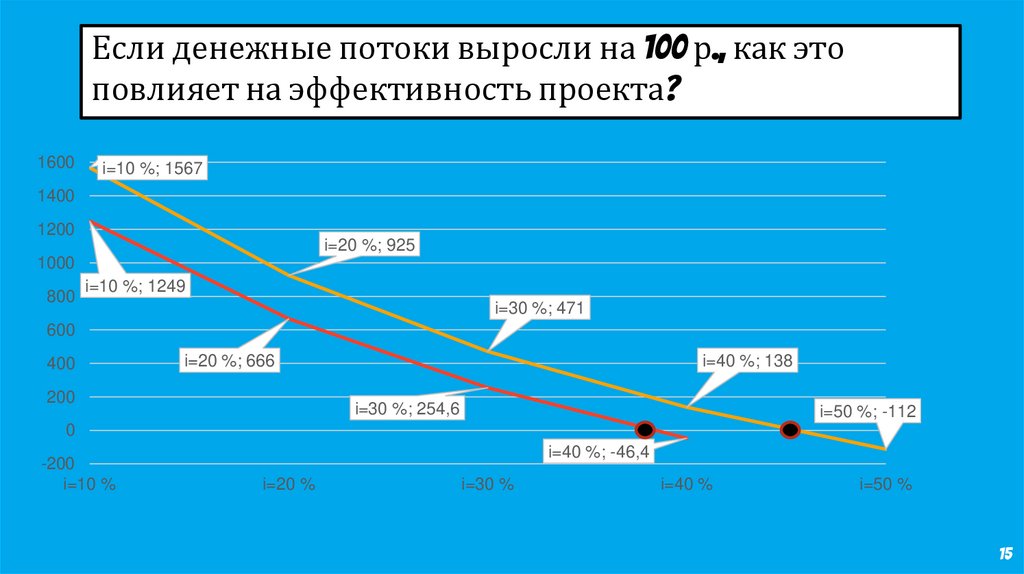
Если денежные потоки выросли на 100 р., как это
повлияет на эффективность проекта?
1600
i=10 %; 1567
1400
1200
i=20 %; 925
1000
800
i=10 %; 1249
i=30 %; 471
600
400
i=20 %; 666
200
i=40 %; 138
i=30 %; 254,6
i=50 %; -112
0
-200
i=10 %
i=40 %; -46,4
i=20 %
i=30 %
i=40 %
i=50 %
15

16.

Решаем
задачи
16

17.

Денежные
потоки
0
1
2
3
4
-200 000
15000
55000
84000
120000
Определите внутреннюю норму рентабельности и сделайте вывод о
степени выгодности проекта.
NPV i=10%
NPV i=20 %
NPV i=15 %
NPV i=11 %
4162,96701
-42 824,07 ₽
-21 526,87 ₽
-1 379,46 ₽
IRR= 0,108=10,8%
17

18.

Найти внутреннюю норму рентабельности и сделать
вывод об эффективности проекта.
Денежные
потоки
% ставка
% ставка
% ставка
% ставка
NPV
NPV
NPV
NPV
0
1
2
3
4
-65000
0,1
0,20 ₽
0,4
0,6
118672,56
77 708,33 ₽
27 815,49 ₽
100,10 ₽
15000
55000
84000
90000
Вывод?
18

19.

×
×
Расчет IRR не требует ставки дисконтирования
NPV - абсолютный показатель, поэтому он не
может дать информации о «запасе прочности»
проекта. Подобную информацию предоставляет
анализ IRR (чем выше IRR цены капитала, тем
выше безопасность). То есть с позиции риска
проекты можно сравнивать по IRR, но не по NPV.
19

20.

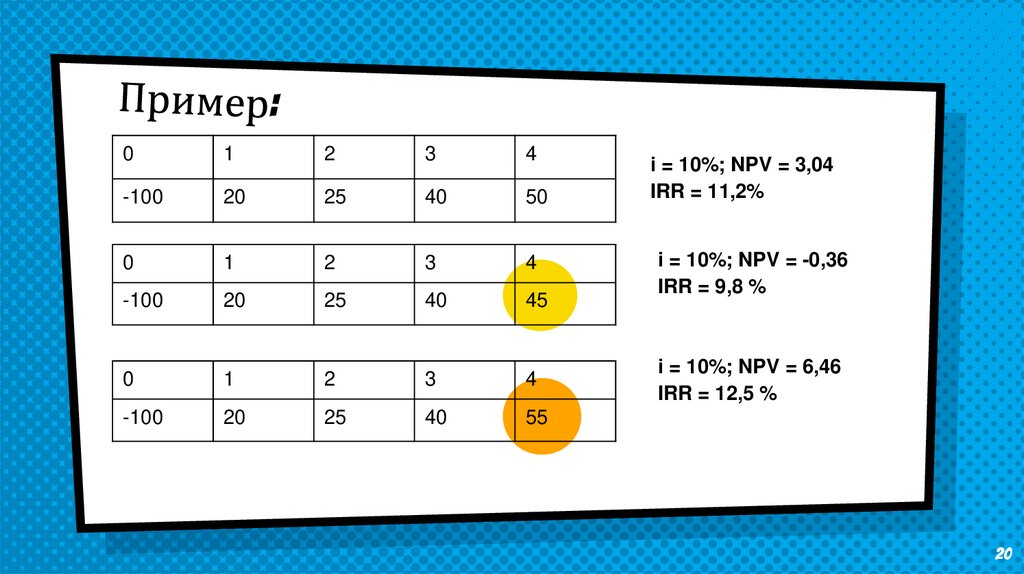
0
1
2
3
4
-100
20
25
40
50
0
1
2
3
4
-100
20
25
40
45
0
1
2
3
4
-100
20
25
40
55
i = 10%; NPV = 3,04
IRR = 11,2%
i = 10%; NPV = -0,36
IRR = 9,8 %
i = 10%; NPV = 6,46
IRR = 12,5 %
20

21.

×
IRR является относительным показателем,
и на его основе невозможно сделать
выводы об альтернативных проектах с
позиции их вклада в увеличение капитала.
21

22.

0
1
2
3
4
-100
20
25
40
50
0
1
2
3
4
-100
20
25
40
55
i = 10%; NPV = 3,04
IRR = 11,2%
i = 10%; NPV = 6,46
IRR = 12,5 %
Если максимальная стоимость портфеля 150 руб., то по
показателю IRR невозможно оценить, каков вклад
отдельных проектов в портфель.
22

23.

0
1
2
3
4
(1) -100
20
25
40
50
(1): i = 10%; NPV = 3,04
IRR = 11,2%
(2) -100
20
25
40
55
(2) i = 10%; NPV = 6,46
IRR = 12,5 %
Включим в портфель проект 2 и ½ от проекта 1.
(2+1/2*1): i=10 %,
NPV=6,46+1/2*3,04 =7,98
IRR= 12,86 %
Если максимальная стоимость портфеля 150 руб., то по
показателю IRR невозможно оценить, каков вклад
отдельных проектов в портфель.
23

24.

× NPV обладает
свойством
аддитивности;
× IRR не обладает
свойством
аддитивности.
24

25.

×
IRR показывает лишь максимальную стоимость
капитала проекта.
0
1
2
3
IRR, %
Проект А
-500
470
150
10
20,3
Проект В
-500
30
250
440
15,4
Сравнить проекты, если i = 8%; i = 12%
25

26.

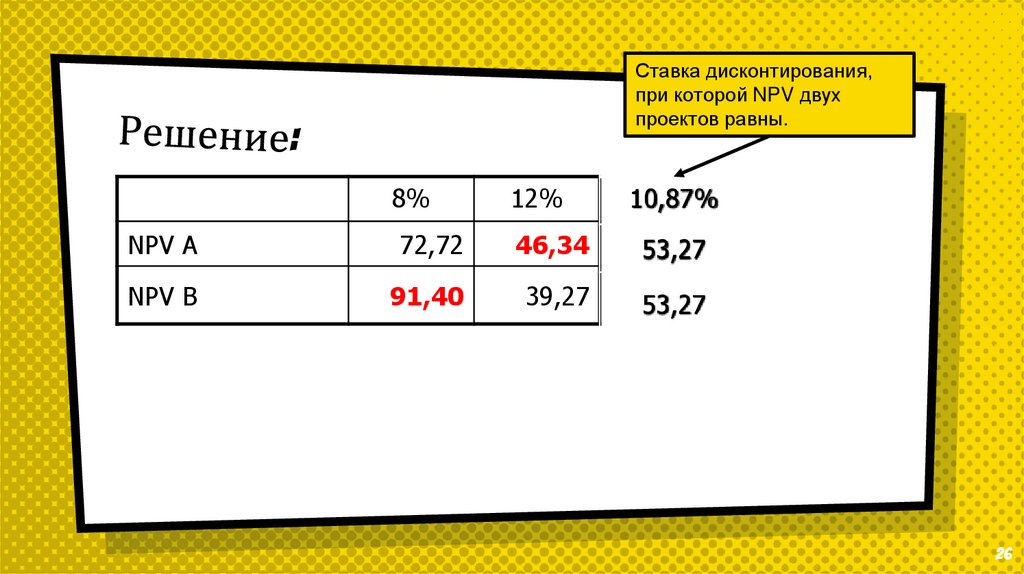
Ставка дисконтирования,
при которой NPV двух
проектов равны.
8%
12%
10,87%
NPV А
72,72
46,34
53,27
NPV В
91,40
39,27
53,27
26

27.

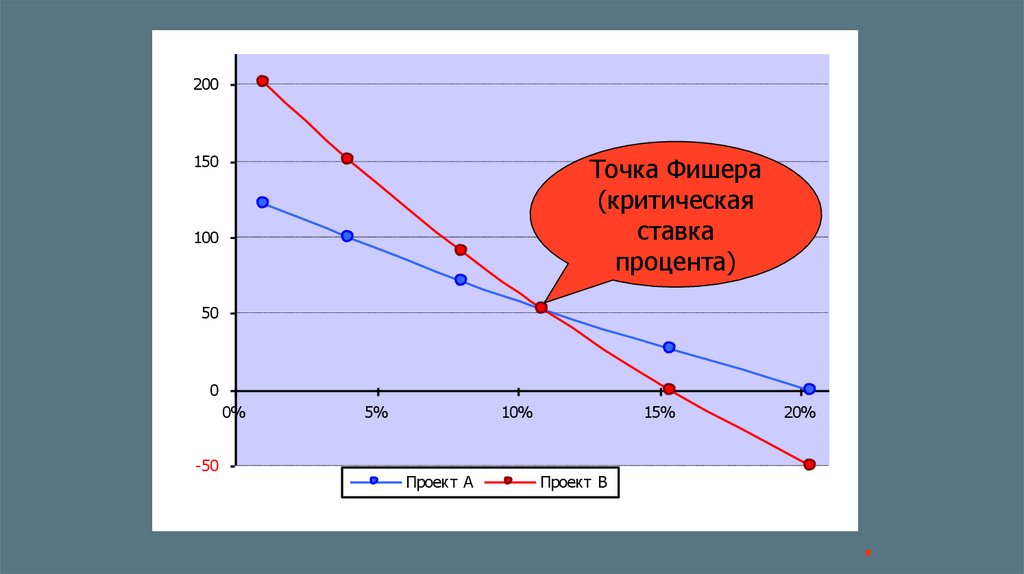
200
150
Точка Фишера
(критическая
ставка
процента)
100
50
0
0%
-50
5%
10%
Проект А
15%
20%
Проект В
.

28.

Точка Фишера находится как IRR
«разностного проекта»
Проект А
Проект В
Проект «В – А»
0
-500
-500
0
1
470
30
-440
2
150
250
100
3
IRR
10 20,3%
440 15,4%
430 10,87%
.

29.

×
IRR нельзя использовать для проектов с неординарными
денежными потоками.
0
1
2
3
IRR, %
А
200
-350
500
-400
11,6
В
-200
350
-500
400
11,6
29

30.

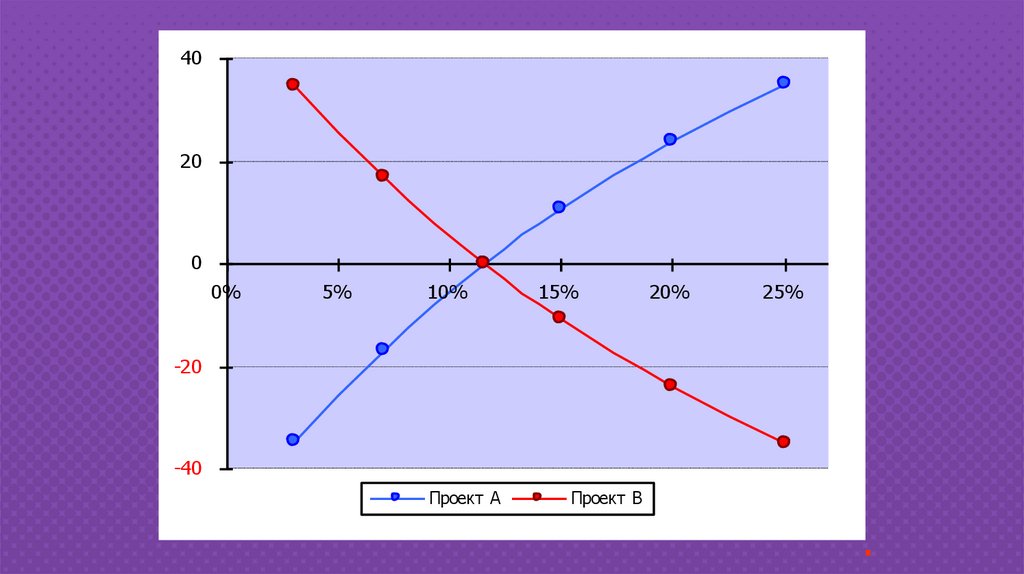
40
20
0
0%
5%
10%
15%
20%
25%
-20
-40
Проект А
Проект В
.

31.

0
1
2
3
IRR, %
А
200
-350
500
-400
11,6
В
-200
350
-500
400
11,6
31

32.

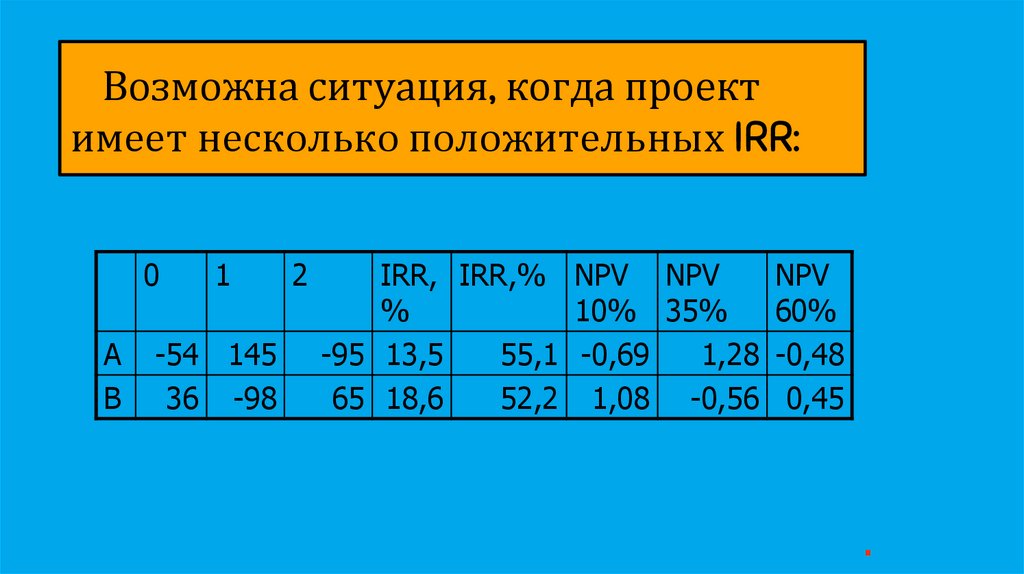
Возможна ситуация, когда проект
имеет несколько положительных IRR:
0
А
В
1
-54 145
36 -98
2
IRR, IRR,% NPV NPV
NPV
%
10% 35%
60%
-95 13,5
55,1 -0,69
1,28 -0,48
65 18,6
52,2 1,08 -0,56 0,45
.

33.

2
1
0
0%
10%
20%
30%
40%
50%
60%
-1
-2
Проект А
Проект В
.

34.

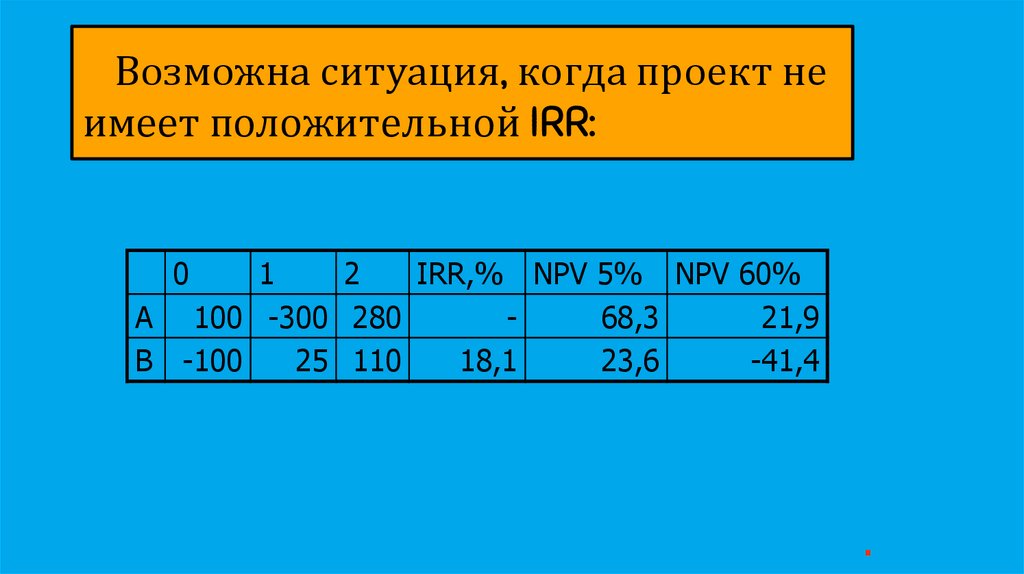
Возможна ситуация, когда проект не
имеет положительной IRR:
0
1
2
IRR,% NPV 5% NPV 60%
А 100 -300 280
68,3
21,9
В -100
25 110
18,1
23,6
-41,4
.

35.

80
60
40
20
0
0%
10%
20%
30%
40%
50%
60%
-20
-40
-60
Проект А
Проект В
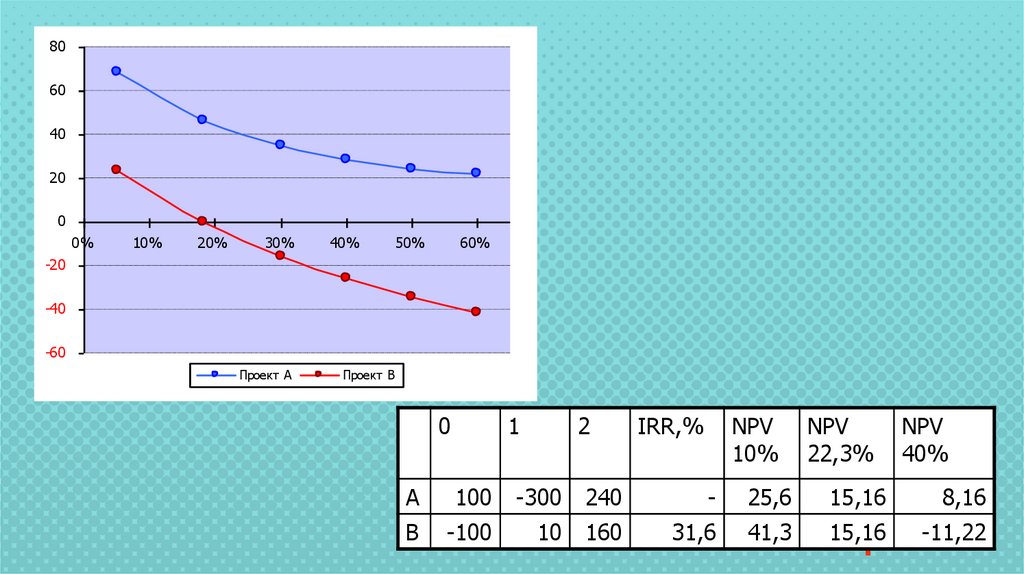
0
1
2
IRR,%
NPV
10%
NPV
22,3%
NPV
40%
А
100
-300
240
-
25,6
15,16
8,16
В
-100
10
160
31,6
41,3
15,16
.
-11,22

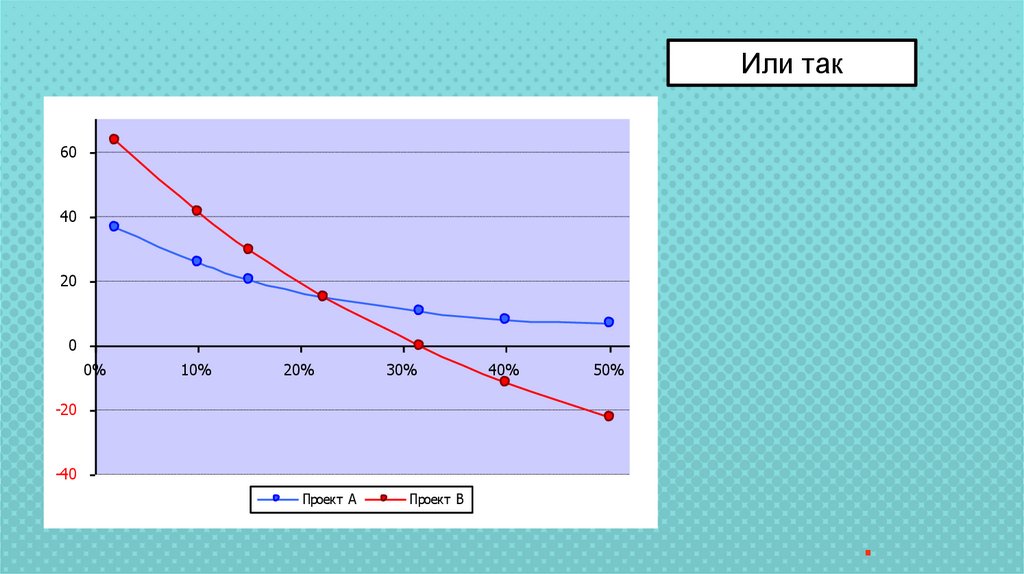
36.

Или так
60
40
20
0
0%
10%
20%
30%
40%
50%
-20
-40
Проект А
Проект В
.

37.

Поэтому показатель
IRR дополняется
другими методами
оценки инвестиций.
37

38.

× IRR показывает
средний ежегодный
прирост результатов
относительно
первоначальных
инвестиций.
38

39.

-I
×
CF1
CF2
CF3
I=CF/(1+IRR)^1+CF/(1+IRR)^2+CF/(1+IRR)^3
Уменьшенные с помощью дисконтирования положительные денежные потоки
равны первоначальным инвестициям. Т.е. фактически за весь срок
положительные денежные потоки вырастут на ставку IRR относительно суммы
инвестиций.
39

40.

×
×
×
×
-200 000
25 000
55 000
84 000
120 000
IRR=0,1254
25000(1+0,1254)^1+55000(1+0,1254)^2+84000/(1+0,1254)^3+120000/(1+0,1254
)^4=199379,5
200000 примерно равно 199379,5, то есть
Инвестиции вырастут на ставку IRR ежегодно и достигнут к концу срока
сумме капитализированных денежных потоков.
-I
CF
CF
CF
CF
40

41.

× По ставке IRR
денежные потоки
каждого года
реинвестируются.
41

42.

× На основании IRR
проекты можно
сравнивать, если у
них одинаковые
инвестиции
42

43.

0
-200000
-200000
×
×
×
1
15000
25000
2
55000
55000
3
84000
84000
4
120000
120000
Сравним проекты при ставке 10 %
NPV1 = 4162,96701 NPV2 = 13253,8761
IRR1 = 0,10810236 IRR2 = 0,12540508
43

44.

×
×
×
×
×
IRR характеризует риск изменения ставки дисконтирования;
IRR показывает доходность инвестиций при реинвестировании
положительных денежных потоков внутри проекта;
IRR можно использовать при сравнении проектов одинаковой
стоимости инвестиций;
IRR не обладает свойством аддитивности;
IRR не используется для проектов с неординарными денежными
потоками.
44

45.

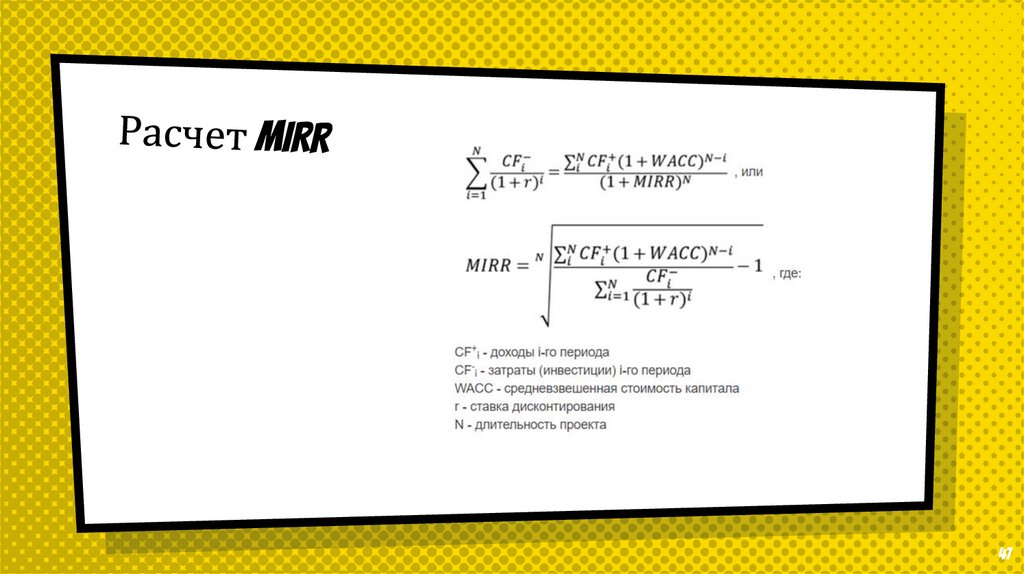
Модифицированная
внутренняя норма
доходности
MIRR

46.

× Подходит для проектов с неординарными
×
денежными потоками;
Основан на разделении ставок
финансирования и доходности вложений.
46

47.

47

48.

-I
CF1
CF2
-I
CF3
CF4
48

49.

Дисконтированный
срок окупаемости
проекта

50.

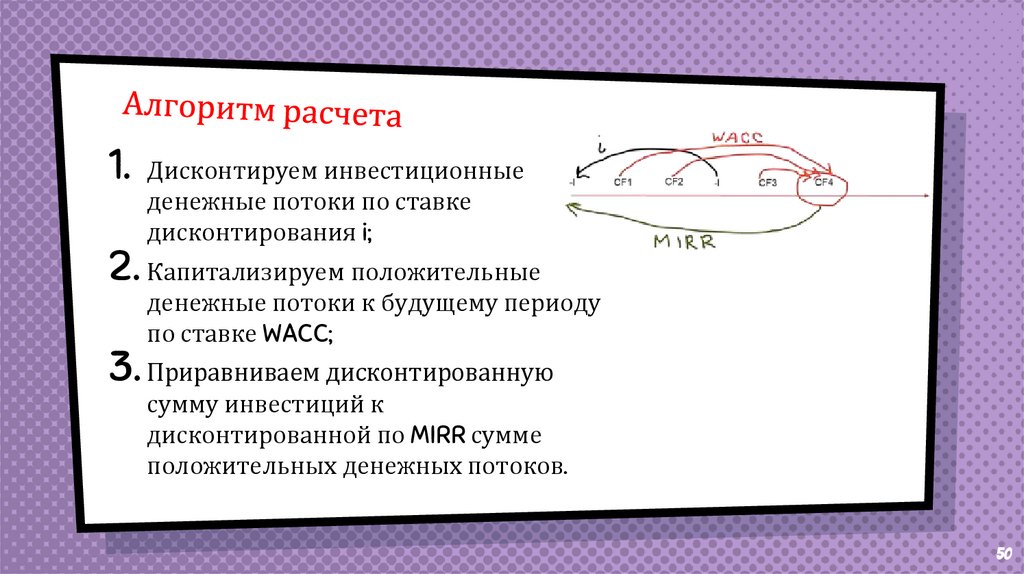
1. Дисконтируем инвестиционные
денежные потоки по ставке
дисконтирования i;
2. Капитализируем положительные
денежные потоки к будущему периоду
по ставке WACC;
3. Приравниваем дисконтированную
сумму инвестиций к
дисконтированной по MIRR сумме
положительных денежных потоков.
50

51.

×
×
×
×
Срок, когда дисконтированные денежные потоки от
проекта станут равны величине первоначальных
инвестиций.
Смысл:
если финансируем за счет кредита, срок когда его отдадим;
если финансируем за счет собственных средств, срок когда доход
станет больше, чем доход по депозиту.
51

52.

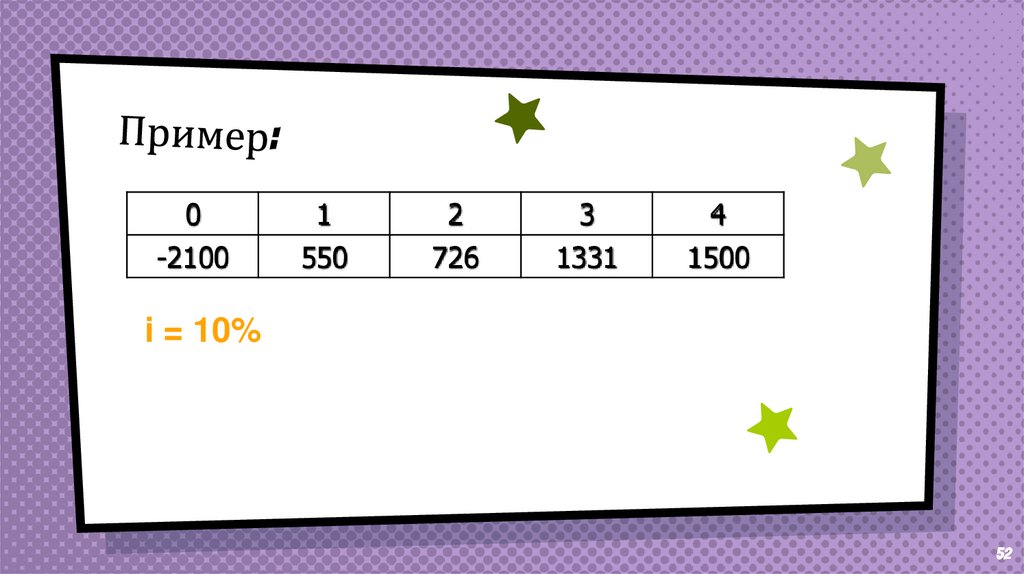
0
-2100
1
550
2
726
3
1331
4
1500
i = 10%
52

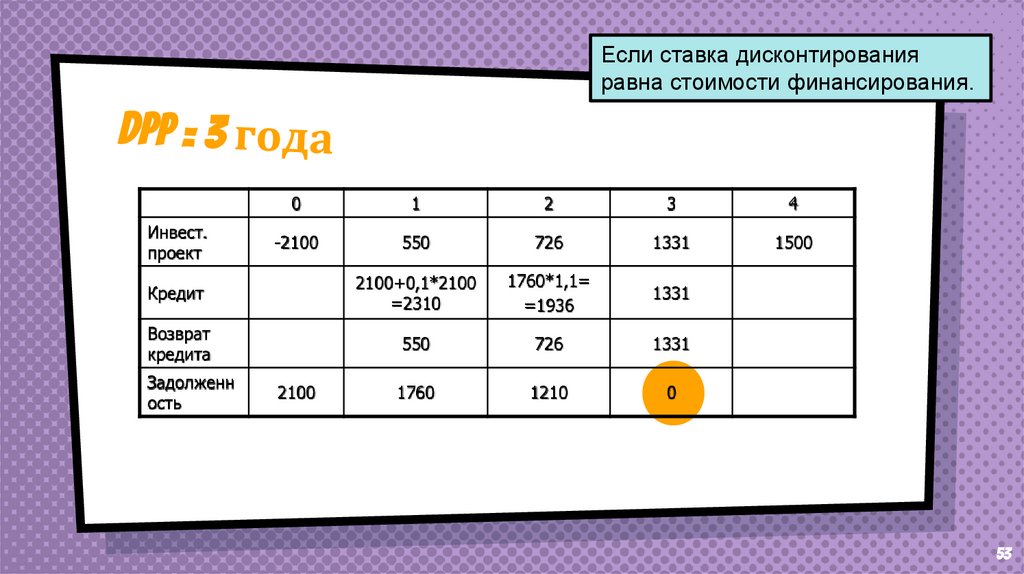
53.

Если ставка дисконтирования
равна стоимости финансирования.
0
1
2
3
4
-2100
550
726
1331
1500
Кредит
2100+0,1*2100
=2310
1760*1,1=
=1936
1331
Возврат
кредита
550
726
1331
1760
1210
0
Инвест.
проект
Задолженн
ость
2100
53

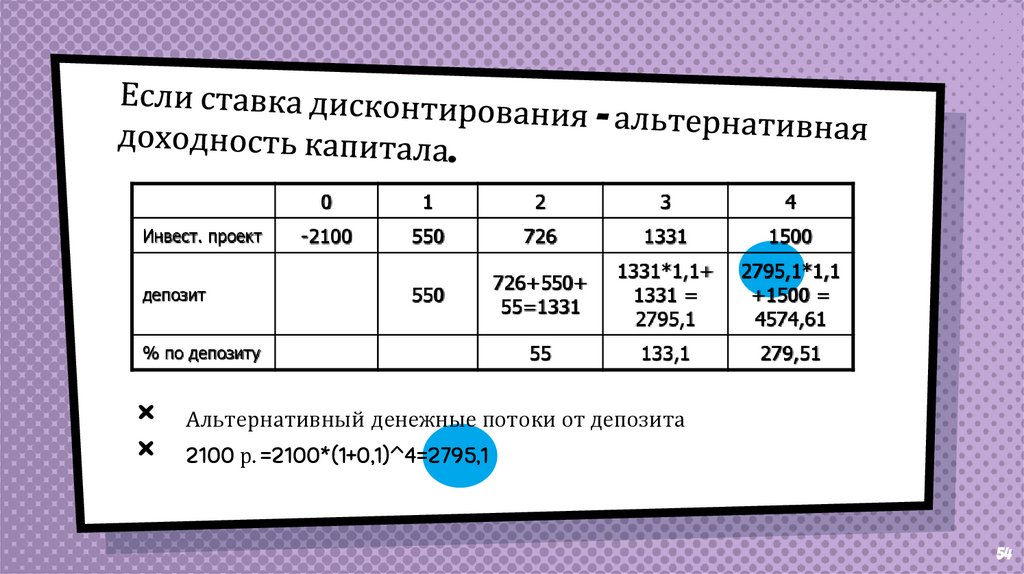
54.

Инвест. проект
депозит
0
1
2
3
4
-2100
550
726
1331
1500
550
726+550+
55=1331
1331*1,1+
1331 =
2795,1
2795,1*1,1
+1500 =
4574,61
55
133,1
279,51
% по депозиту
×
×
Альтернативный денежные потоки от депозита
2100 р. =2100*(1+0,1)^4=2795,1
54

55.

Спасибо!
Сразу стало все понятно
55