Методы поэлементной обработки изображений

1.

Саратовский государственный технический университет
Кафедра: Прикладные информационные технологии
МЕТОДЫ ПОЭЛЕМЕНТНОЙ ОБРАБОТКИ
ИЗОБРАЖЕНИЙ
Саратов 2015
1

2. неоднородное преобразование

Сущность поэлементной обработки изображений
сводится к следующему. Пусть x(i,j), y(i,j) значения яркости исходного и обработанного
изображений соответственно в точке кадра,
имеющей декартовы координаты i (номер строки)
и j (номер столбца).
Поэлементная обработка означает, что существует
функциональная однозначная зависимость между
этими яркостями:
yi , j f i , j ( xi , j )
неоднородное преобразование
y f ( x)
однородное преобразование
2

3. Линейное контрастирование изображения

Задача
контрастирования
связана
с
улучшением
согласования динамического диапазона изображения и
экрана, на котором выполняется визуализация.
Предположим, что минимальная и максимальная яркости
исходного изображения равны Xmin, и
Xmax
соответственно.
Пример такого неудачного представления приведен на рис.
где диапазон яркостей имеет границы Xmin=180,
Xmax=240.
При линейном контрастировании используется линейное
поэлементное преобразование вида:
y a x b
3

4. Линейное контрастирование изображения

параметры a и b которого и определяются желаемыми
значениями минимальной Ymin и максимальной Ymax
выходной яркости. Решив систему уравнений:
ymin a xmin b
ymax a xmax b
,:
относительно параметров преобразования нетрудно
привести исходное уравнение к виду
x xmin
y
( ymax ymin ) ymin
xmax xmin
4

5. Результат линейного контрастирования исходного изображения, представленного на левом рис., приведен на правом рис. при Ymin=0 и

Ymax=255
5

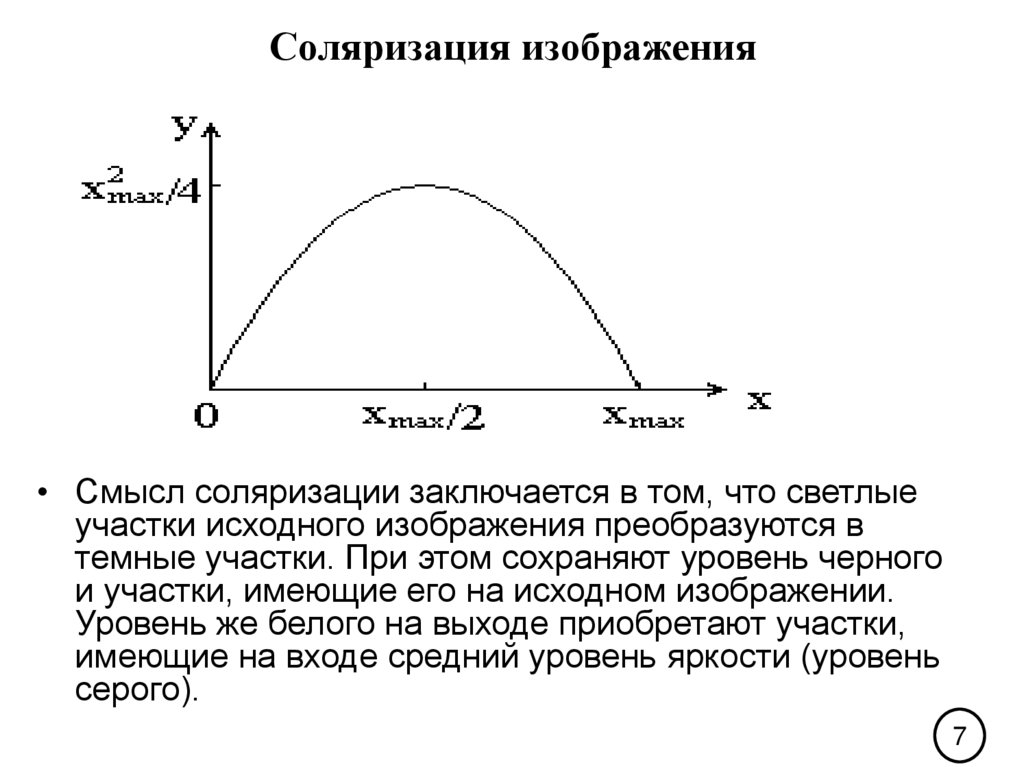
6. Соляризация изображения

При данном виде обработки преобразование имеет вид:
y k x ( xmax x)
где Xmax- максимальное значение исходного сигнала, а
K - константа, позволяющая управлять динамическим
диапазоном преобразованного изображения. Функция,
описывающая данное преобразование, является
квадратичной параболой, ее график при K=1 приведен
на рис. При Ymax=Xmax динамические диапазоны
изображений совпадают, что может быть достигнуто при
K=4/Xmax
6

7. Соляризация изображения

• Смысл соляризации заключается в том, что светлые
участки исходного изображения преобразуются в
темные участки. При этом сохраняют уровень черного
и участки, имеющие его на исходном изображении.
Уровень же белого на выходе приобретают участки,
имеющие на входе средний уровень яркости (уровень
серого).
7

8. Пример применения соляризации

Обработка приводит к повышению четкости деталей
изображения: улучшены изображения глаз, повышен
контраст на переходе лицо - волосы и т. д..
8

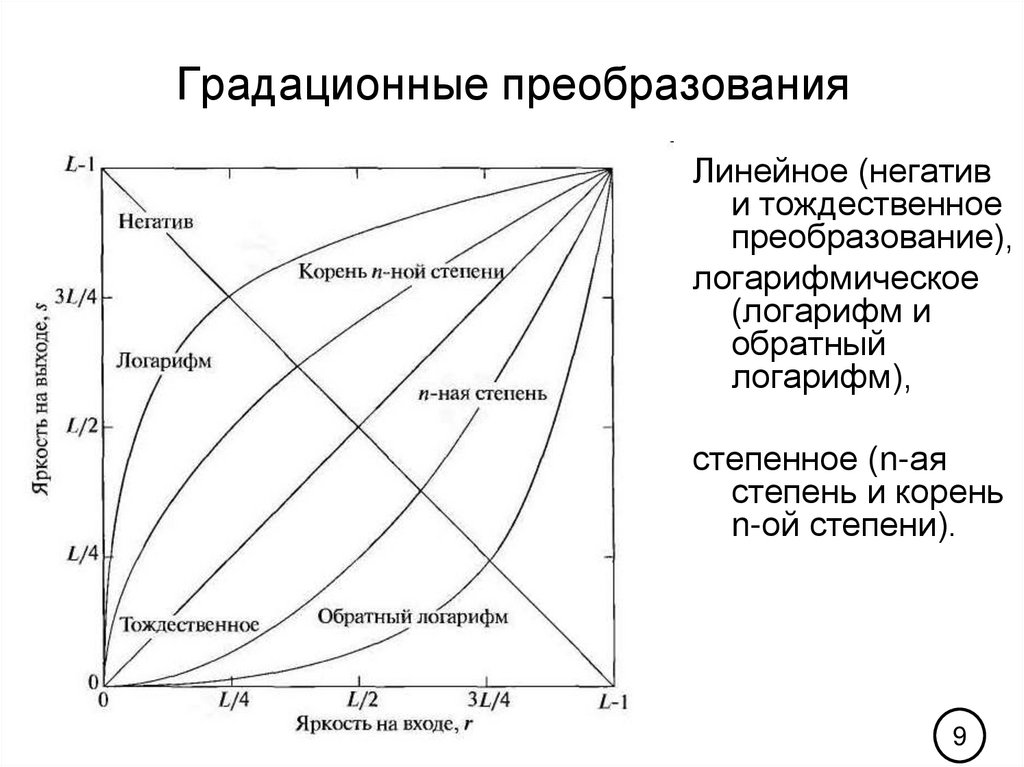
9. Градационные преобразования

Линейное (негатив
и тождественное
преобразование),
логарифмическое
(логарифм и
обратный
логарифм),
степенное (n-ая
степень и корень
n-ой степени).
9

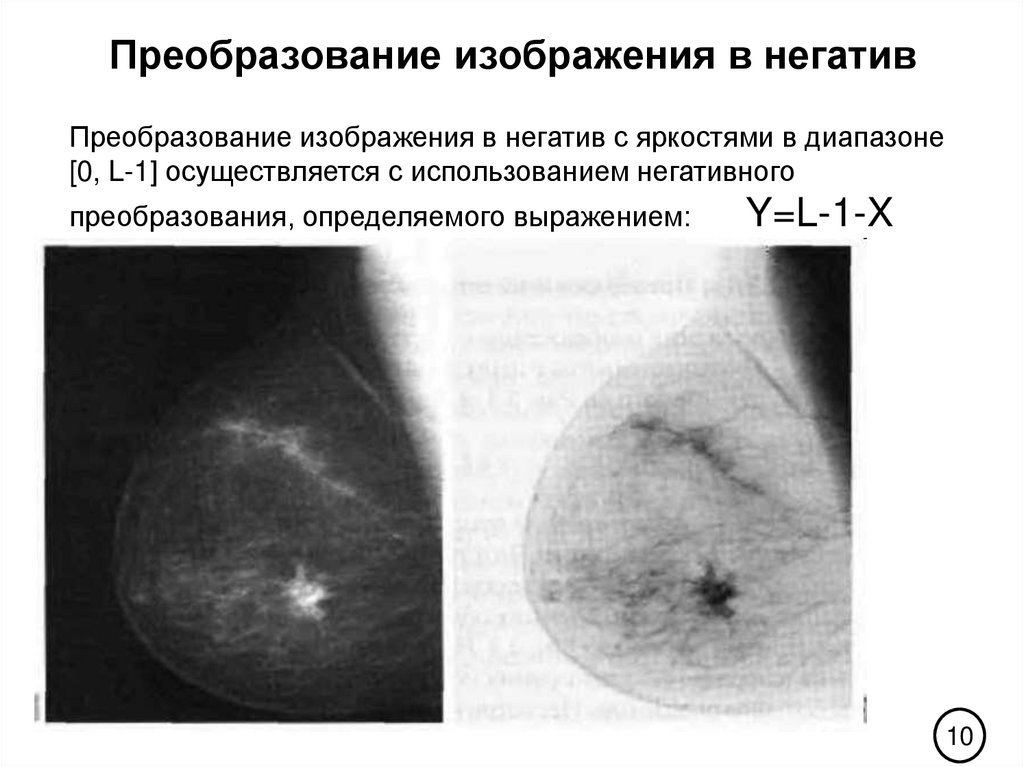
10. Преобразование изображения в негатив

Преобразование изображения в негатив с яркостями в диапазоне
[0, L-1] осуществляется с использованием негативного
преобразования, определяемого выражением:
Y=L-1-X
10

11. Логарифмическое преобразование

Общий вид логарифмического преобразования, показанного на
Рис. (см: слайд 9), выражается формулой
Y= c log(X + r),
где с — константа и предполагается, что r > 0.
Форма логарифмической кривой показывает, что данное
преобразование отображает узкий диапазон малых значений
яркостей на исходном изображении в более широкий диапазон
выходных значений. Для больших значений входного сигнала
верно противоположное утверждение.
Наоборот, при использовании обратного логарифмического
преобразования происходит растяжение диапазона ярких
пикселей и сжатие диапазона темных пикселей.
11

12. Логарифмическое преобразование

Классическим примером, в котором значения пикселей имеют большой
динамический диапазон, является спектр Фурье, значения которого
изменяются в диапазоне от 0 до 1000000 или более, не является чем-то
необычным, однако система воспроизведения изображений обычно не
способна правильно отобразить столь большой диапазон значений
интенсивности. Результирующий эффект таков, что при обычном
воспроизведении спектра Фурье значительное число деталей теряется.
12

13. Степенные преобразования

Степенные
преобразования
имеют вид
где с и γ являются
положительными
константами.
13

14.

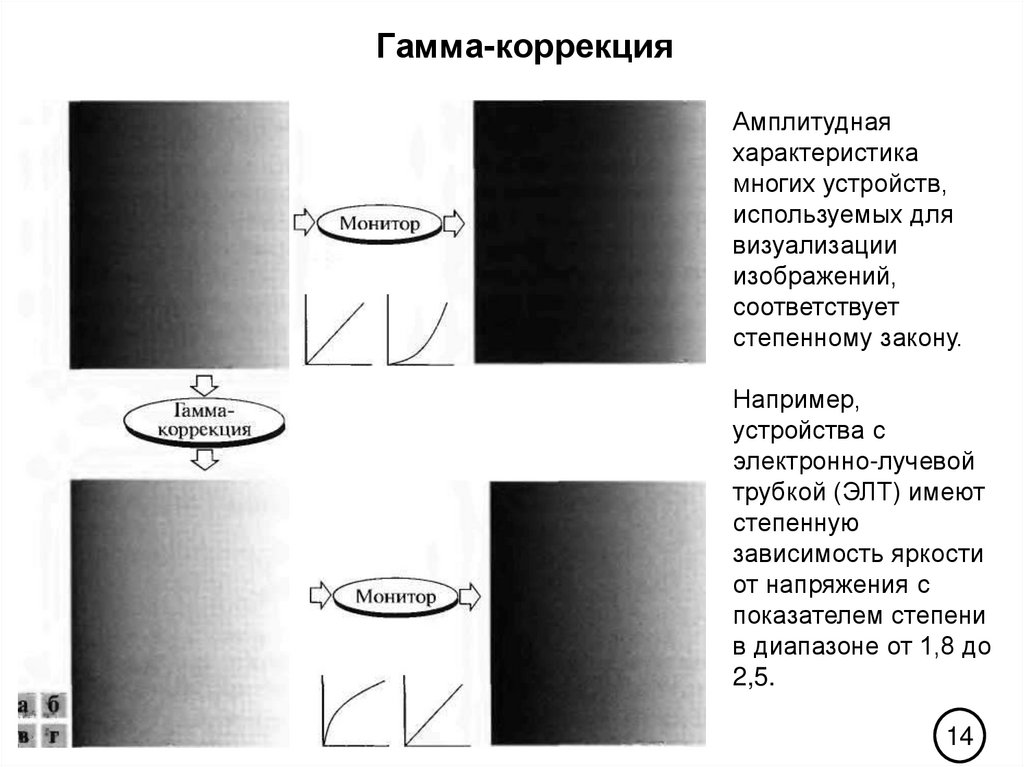
Гамма-коррекция
Амплитудная
характеристика
многих устройств,
используемых для
визуализации
изображений,
соответствует
степенному закону.
Например,
устройства с
электронно-лучевой
трубкой (ЭЛТ) имеют
степенную
зависимость яркости
от напряжения с
показателем степени
в диапазоне от 1,8 до
2,5.
14

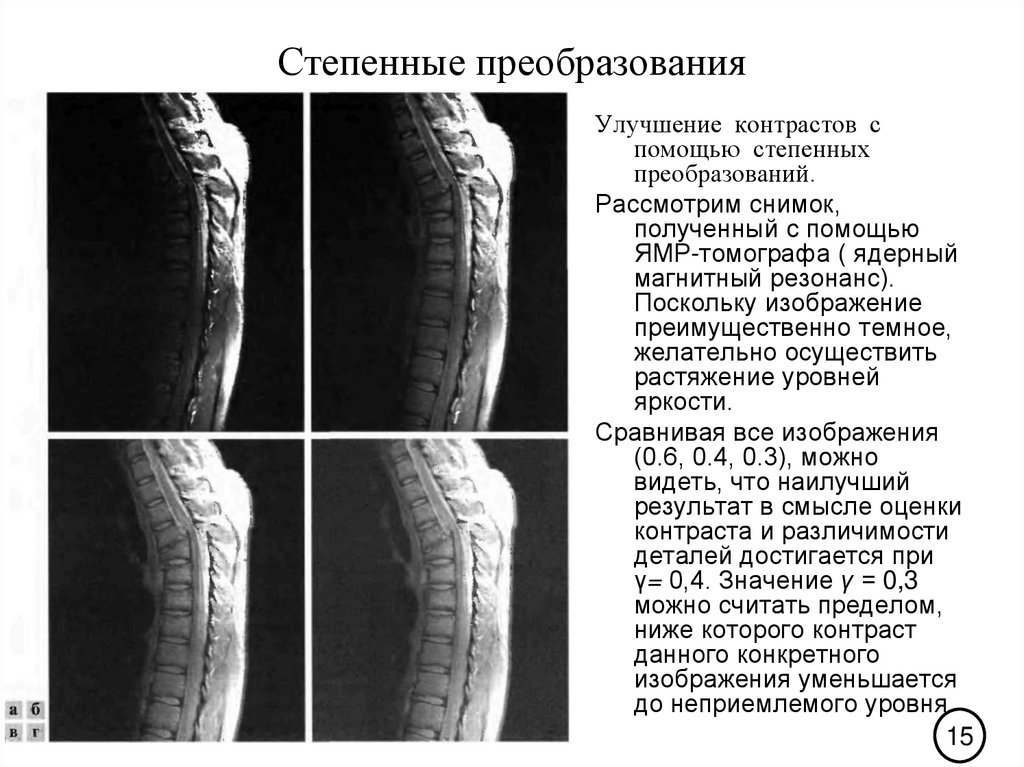
15. Степенные преобразования

Улучшение контрастов с
помощью степенных
преобразований.
Рассмотрим снимок,
полученный с помощью
ЯМР-томографа ( ядерный
магнитный резонанс).
Поскольку изображение
преимущественно темное,
желательно осуществить
растяжение уровней
яркости.
Сравнивая все изображения
(0.6, 0.4, 0.3), можно
видеть, что наилучший
результат в смысле оценки
контраста и различимости
деталей достигается при
γ= 0,4. Значение γ = 0,3
можно считать пределом,
ниже которого контраст
данного конкретного
изображения уменьшается
до неприемлемого уровня.
15

16. Степенные преобразования

В данном случае
требуется понизить
яркость. Это
достигается со
значениями γ больше 1.
Результаты обработки
изображения при γ —
3,0, 4,0 и 5,0.
Подходящие результаты
достигаются при
значениях гамма 3,0 и
4,0, причем последний
вариант выглядит более
предпочтительным. На
изображении, при γ =
5,0, имеются слишком
темные области, на
которых часть деталей
утеряна.
16

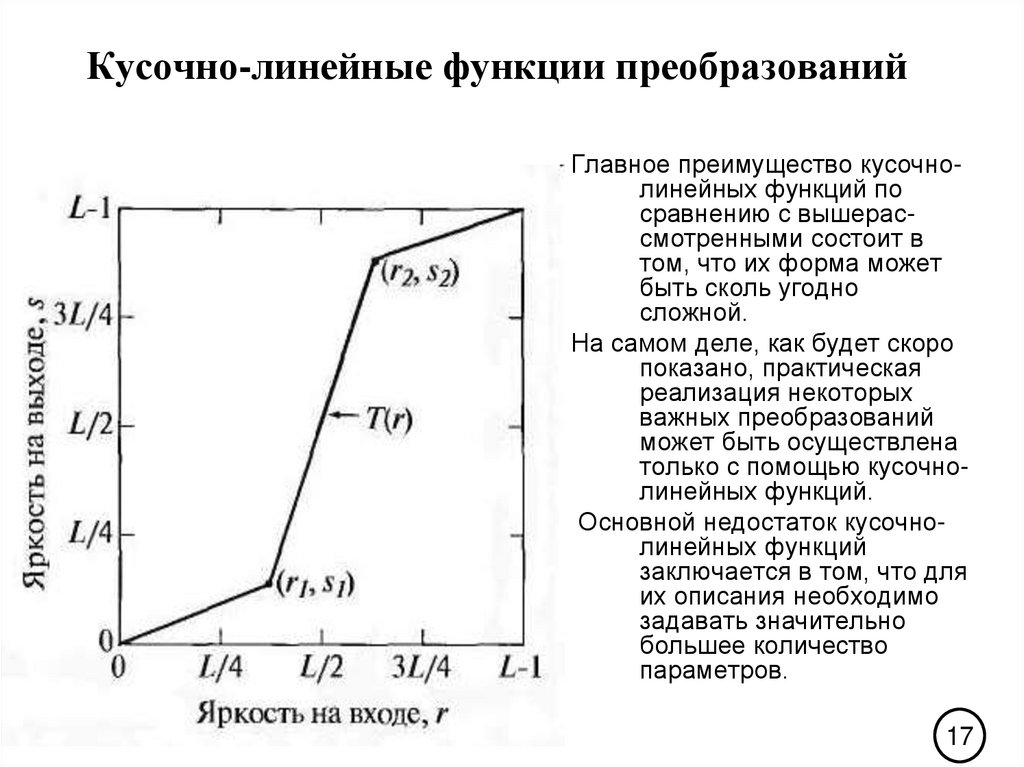
17. Кусочно-линейные функции преобразований

Главное преимущество кусочнолинейных функций по
сравнению с вышерассмотренными состоит в
том, что их форма может
быть сколь угодно
сложной.
На самом деле, как будет скоро
показано, практическая
реализация некоторых
важных преобразований
может быть осуществлена
только с помощью кусочнолинейных функций.
Основной недостаток кусочнолинейных функций
заключается в том, что для
их описания необходимо
задавать значительно
большее количество
параметров.
17

18. Кусочно-линейные функции преобразований

Представлено (справо) исходное малоконтрастное 8-битовое
изображение. На левом рис показан результат усиления контраста,
полученный при (r1, s1) = (Rmin, 0) и (r2, s2) = (Rmax, L-1), где Rmin и
Rmax, соответственно, означают минимальную и максимальную
яркости на изображении. Таким образом, функция преобразования
линейно растягивает исходный диапазон яркостей в полный
диапазон [0, L-1 ].
18

19. Препарирование изображения

Препарирование представляет собой целый класс поэлементных
преобразований изображений. Характеристики применяемых
на практике процедур препарирования приведены на рис.
19

20. Препарирование изображения.

Препарирование часто используется и в
автоматических системах обработки
визуальной информации, поскольку
подготавливаемый при этом препарат может
содержать всю информацию, необходимую
для последующей (вторичной) обработки.
20

21. Преобразование гистограмм, эквализация

В практике цифровой обработки изображений часто к полезному результату
приводит преобразование изображения к равновероятному распределению.
В этом случае
1 ymax ymin ,
wy ( y)
0,
,
при ymin y ymax ,
при других y ,
где
Wy(y) – плотность вероятности, Ymin, Ymax - минимальное и
максимальное значения яркости преобразованного изображения. Определим
характеристику преобразователя, решающего данную задачу. Пусть x и y
связаны функцией y=f(x), а Fx(x)
и Fy(y) - интегральные законы
распределения входной и выходной величин. Учитывая значение Wy(y),
находим:
y
y ymin
Fy ( y ) wy ( y)dy
ymax ymin
y min
Подставляя это выражение в условие вероятностной эквивалентности
Fx ( x) = Fy ( y)
21

22. Преобразование гистограмм, эквализация

после простых преобразований получаем соотношение
y ( ymax ymin ) Fx ( x) ymin
,
Таким образом, в практике обработки изображений преобразование
распределений выполняют в два этапа.
На первом этапе измеряется гистограмма исходного изображения.
Каждое значение гистограммы показывает количество точек в кадре,
имеющих данную яркость. Разделив все числа этой таблицы на общий
размер выборки, равный числу используемых точек изображения, получают
оценку распределения вероятностей яркости изображения. Обозначим эту
оценку Wх(х) . Тогда оценка интегрального распределения получается по
j
формуле:
Fx ( j ) w x (i )
i 0
На втором этапе выполняется само нелинейное преобразование (см.
выше),
обеспечивающее
необходимые
свойства
выходного
изображения.
Все
методы
поэлементного
преобразования
изображений, целью которых является видоизменение законов
распределения, получили название гистограммных методов.
21

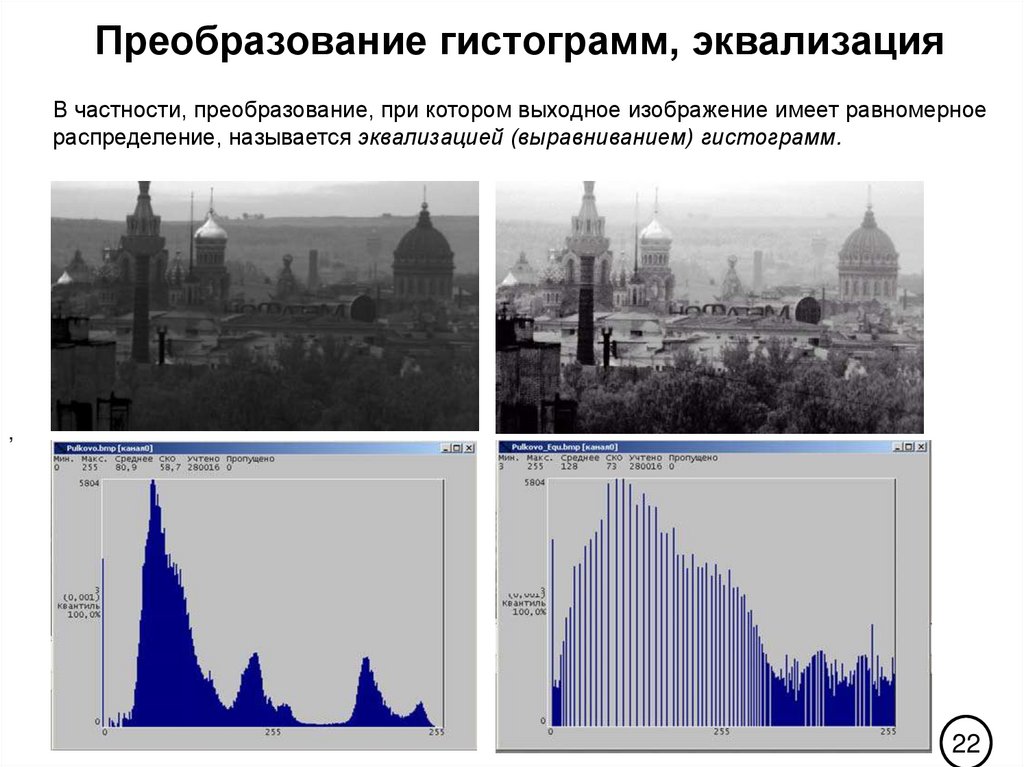
23. Преобразование гистограмм, эквализация

В частности, преобразование, при котором выходное изображение имеет равномерное
распределение, называется эквализацией (выравниванием) гистограмм.
,
22

24. При поэлементных преобразованиях изображений вычисления по формуле Y=F(X) должны быть выполнены для всех точек исходного

Применение табличного метода
при поэлементных преобразованиях изображений
При поэлементных преобразованиях изображений вычисления по
формуле Y=F(X) должны быть выполнены для всех точек исходного
изображения. В тех же задачах, где функция F предполагает трудоемкие
вычисления (умножения, деления, расчеты тригонометрических
выражений, степенных и других функций), применение прямого метода
преобразования яркостей может оказаться вообще неприемлемым.
Сущность табличного метода состоит в том, что путем предварительного
расчета создается таблица функции.
При обработке изображения вместо вычислений используются готовые
результаты путем обращения к этой таблице. При этом значение входной
яркости служит для определения номера столбца, из которого должна
быть считана величина преобразованного сигнала .
23

25. 1. Сущность поэлементной обработки при использовании однородной или неоднородной функции преобразования. 2. Основные параметры

ВОПРОСЫ
1. Сущность поэлементной обработки при
использовании однородной или неоднородной
функции преобразования.
2. Основные параметры при линейном
контрастировании.
3. Для каких изображений целесообразно
проводить линейное контрастирование.
4. Для каких целей проводится соляризация
изображений.
5. Вид функции используемой при соляризации.
6. Виды линейных градационных преобразований
и их применение.
7. Виды логарифмических градационных
преобразований и их применение.
24

26. 8. Виды степенных градационных преобразований и их применений. 9. В чем суть гамма-коррекции. 10. Кусочно-линейные функции. 11.

ВОПРОСЫ
8. Виды степенных градационных преобразований
и их применений.
9. В чем суть гамма-коррекции.
10. Кусочно-линейные функции.
11. Препарирование изображений и их
применение.
12. Что такое гистограмма.
13. Суть эквализации (выравнивание гистограмм).
14. Поясните, почему при эквализации изображения не
удается привести гистограмму к идеальному
равномерному виду ?
15. В чем состоит сущность и каковы достоинства
табличного метода поэлементного преобразования
изображений ?
25